[优选算法专题四.前缀和——NO.27 寻找数组的中心下标]

题目链接：

寻找数组的中心下标

题目描述：

题目解析：

---

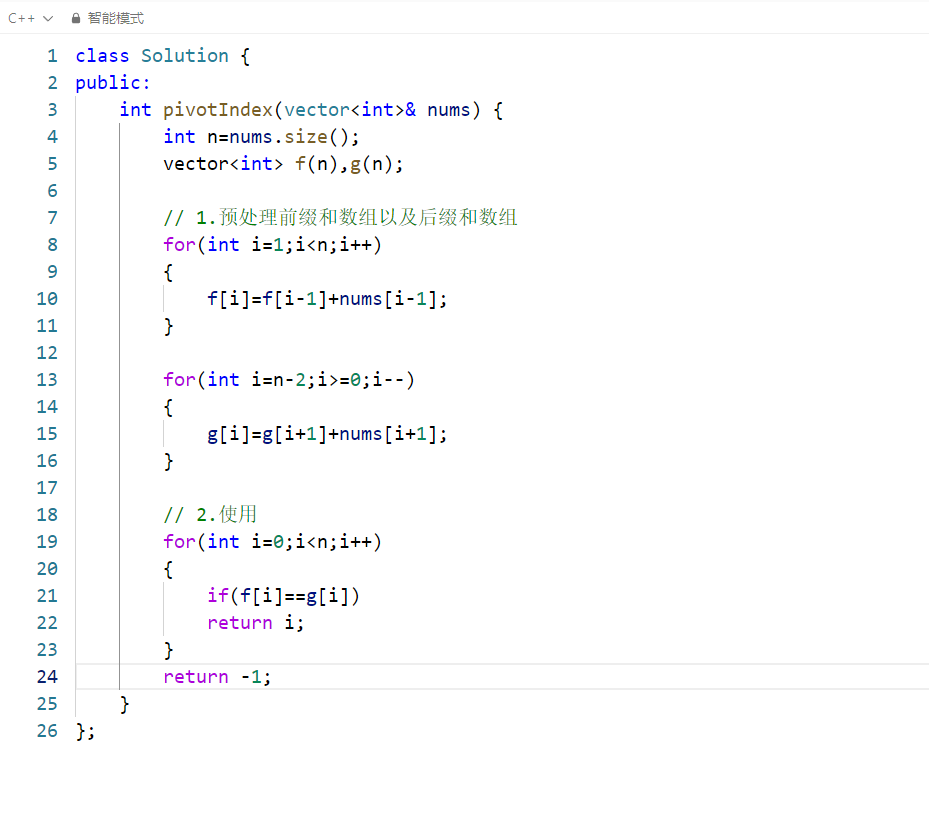
核心思路

通过预处理两个辅助数组：

• 前缀和数组 f：f[i] 表示下标 i 左侧所有元素的总和（不包含 nums[i] 本身）。
• 后缀和数组 g：g[i] 表示下标 i 右侧所有元素的总和（不包含 nums[i] 本身）。

然后遍历数组，判断每个下标 i 的 f[i] 是否等于 g[i]，若相等则 i 即为中心下标。

总结

• 时间复杂度：O(n)，其中 n 是数组长度。预处理两个数组和遍历数组均为线性时间。
• 空间复杂度：O(n)，用于存储前缀和数组 f 和后缀和数组 g（可优化至 O(1)，通过先计算总 sum，再用单变量实时计算左侧和，右侧和 = 总 sum - 左侧和 - 当前元素）。
• 关键点：前缀和与后缀和的定义清晰区分了「不包含当前元素」，避免了重复计算。