【算法】day7 滑动窗口+二分查找

1、滑动窗口最大值 hot

题目：239. 滑动窗口最大值 - 力扣（LeetCode）

分析：

① 暴力解法：左右双指针，遍历 n-k+1 个窗口。每个窗口都要找到最大值，遍历 k 个数字。

时间复杂度：O(kn)   (n-k+1)*k

空间复杂度：O(1)

② 单调性队列：

我们能找到一个单调性规律：如果新元素>窗口中的元素，那么窗口中的较小值必定不是最大值（只要新元素在，较小值都不会是；新元素出窗口了，较小值也必定出窗口了，所以也不会是），都需要删除，直到窗口中元素>新元素或者没有比新元素大的。因此，这个窗口必满足单调递减，窗口首元素必定是窗口中最大值。

因为要频繁获取窗口首（删除出窗口元素、获取最大值）、尾元素（删除较小值），我们使用双端队列。

因为我们需要判断队首元素是否在窗口范围内，所以队列元素不能存元素值，而存 index（队首元素index不能≤ i - k）。

时间复杂度：O(n) 遍历一次数组即可。

空间复杂度：O(k) 队列一直保持其中的元素都是窗口中的元素。

代码：

class Solution {public int[] maxSlidingWindow(int[] nums, int k) {Deque<Integer> queue = new LinkedList<>(); // 双端队列Integer n = nums.length;int[] retMax = new int[n-k+1];// 构造第一个窗口for(int i = 0; i < k; i++) {// 窗口内存在元素，且新元素比窗口内元素大，就一直删除队尾while(!queue.isEmpty() && nums[i] > nums[queue.peekLast()]) queue.pollLast();queue.offerLast(i); // 新元素下标入队列}// 队首元素就是窗口内最大值的下标retMax[0] = nums[queue.peekFirst()];// 遍历剩下的元素，进一次窗口，出一次窗口for(int i = k; i < n; i++) {while(!queue.isEmpty() && nums[i] > nums[queue.peekLast()]) queue.pollLast();queue.offerLast(i);// 删去不符合窗口范围的元素while(queue.peekFirst() <= i-k) queue.pollFirst();// 获取队首最大值下标retMax[i-k+1] = nums[queue.peekFirst()];         }return retMax;}
}

2、搜索插入位置 hot

题目：35. 搜索插入位置 - 力扣（LeetCode）

分析：排序数组、要求时间复杂度O(logn)，二分查找。

如果数组中没有查找值，找第一个大于插入值的位置：分为小于 t 的值（le=x+1）和大于 t 的值（保留最左端 ri=x）。就是查找左端点，没找到，左端点就是第一个比查找值大的值；找到了，左端点就是第一个查找值。

特殊情况：数组里全是小于 t 的数，那么退出循环时，left=right 指向最后一个数，插入位置应该在其后一位。left++。

代码：

class Solution {public int searchInsert(int[] nums, int target) {int left = 0, right = nums.length-1;while(left < right) {int mid = left+(right-left)/2;if(nums[mid] < target) left = mid+1;else right=mid;}if(nums[left] < target) left++;return left;}
}

3、寻找旋转排序数组中的最小值 hot

题目：153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

分析：

旋转后，数组的分布：

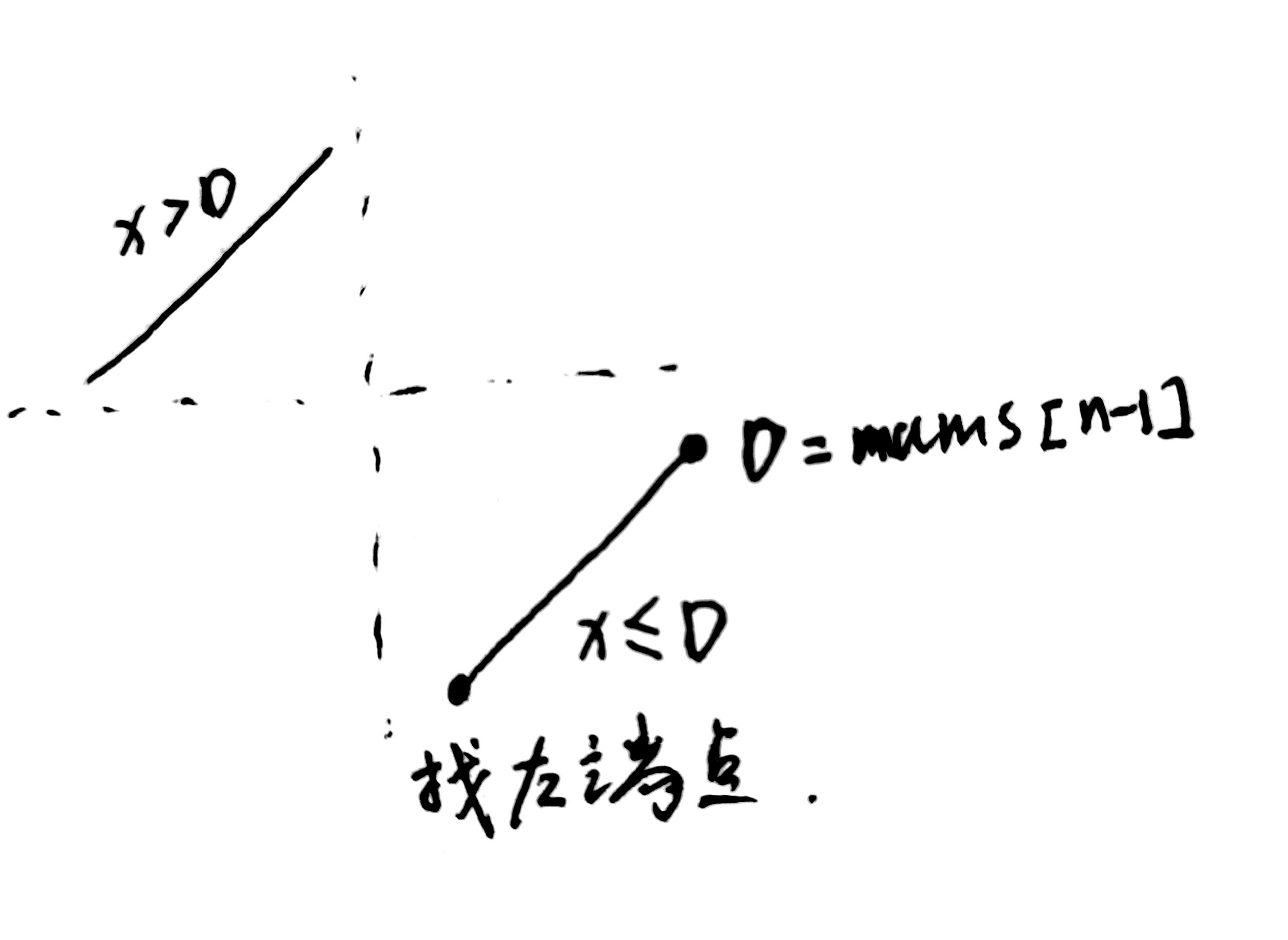
代码：

class Solution {public int findMin(int[] nums) {int left = 0, right = nums.length-1;int t = nums[right];while(left < right) {int mid = left+(right-left)/2;if(nums[mid] > t) left=mid+1;else right=mid;}return nums[left];}
}

4、搜索二维矩阵 hot

题目：74. 搜索二维矩阵 - 力扣（LeetCode）

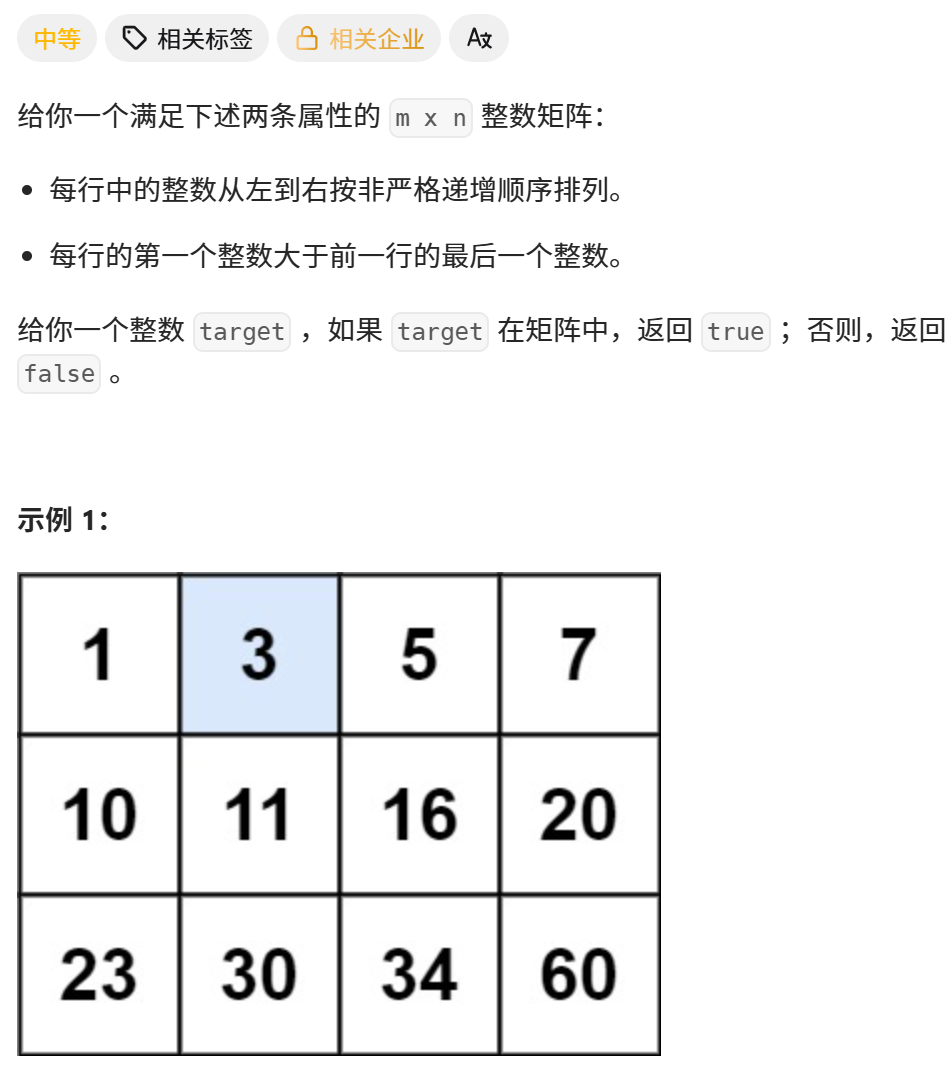
分析：就是朴素二分查找，只不过要把一维坐标映射为二维坐标，来获取矩阵元素值。

代码：

class Solution {// 把一维坐标映射为二维坐标public boolean searchMatrix(int[][] matrix, int target) {int left = 0, right = matrix.length * matrix[0].length-1;int n = matrix[0].length;while(left <= right) {int mid = left+(right-left)/2;if(matrix[mid / n][mid % n] < target) left=mid+1;else if(matrix[mid / n][mid % n] > target) right=mid-1;else return true;}return false;}
}

5、搜索二维矩阵Ⅱ hot

题目：240. 搜索二维矩阵 II - 力扣（LeetCode）

分析：以右上角为分界点 mid，其行它是最大值，其列它是最小值。若 mid < target，行增加；若 mid > target，列减小。(x,y) 越界则未找到。

代码：

class Solution {public boolean searchMatrix(int[][] matrix, int target) {int row = 0, col = matrix[0].length-1;while(row < matrix.length && col >= 0) {int mid = matrix[row][col];if(mid < target) row++;else if(mid > target) col--;else return true;}return false;}
}