当前位置：首页 > news >正文

大话数据结构之＜栈＞和＜队列＞（C语言）

news 2025/10/19 8:05:22

一. 栈

1. 栈的概念及结构

2.栈的实现

二. 队列

1.队列的概念及结构

2. 动态链式队列的实现

3. 静态顺序队列实现（一般教学使用）

3.5 非循环顺序队列的缺点

3.5.1 假溢出（False Overflow）

3.5.2 空间利用率低

4. 循环队列

循环队列的概念

循环队列实现（静态）

🔄 核心机制：循环指针

三. 队列小结

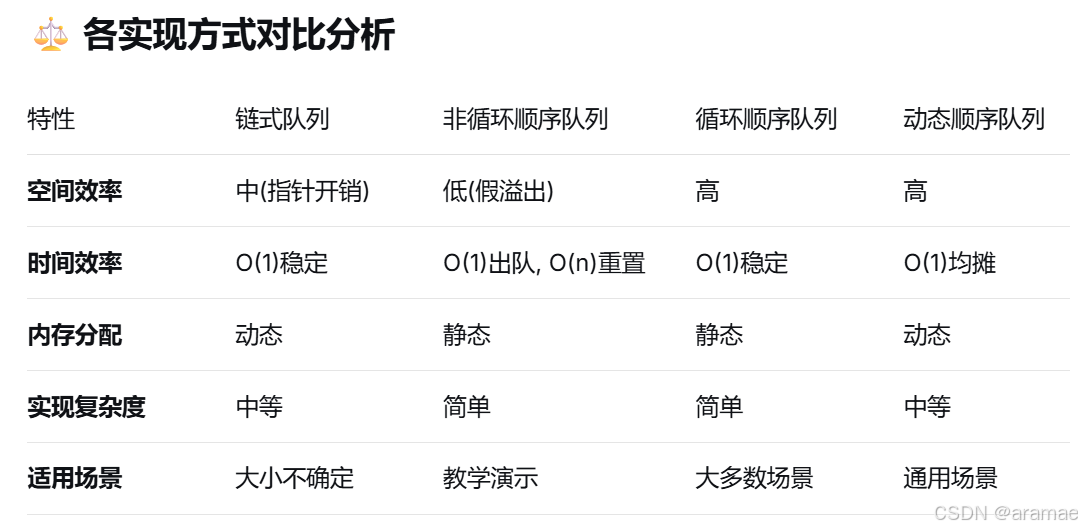
四. 栈 vs 队列：对比总结

一. 栈

1. 栈的概念及结构

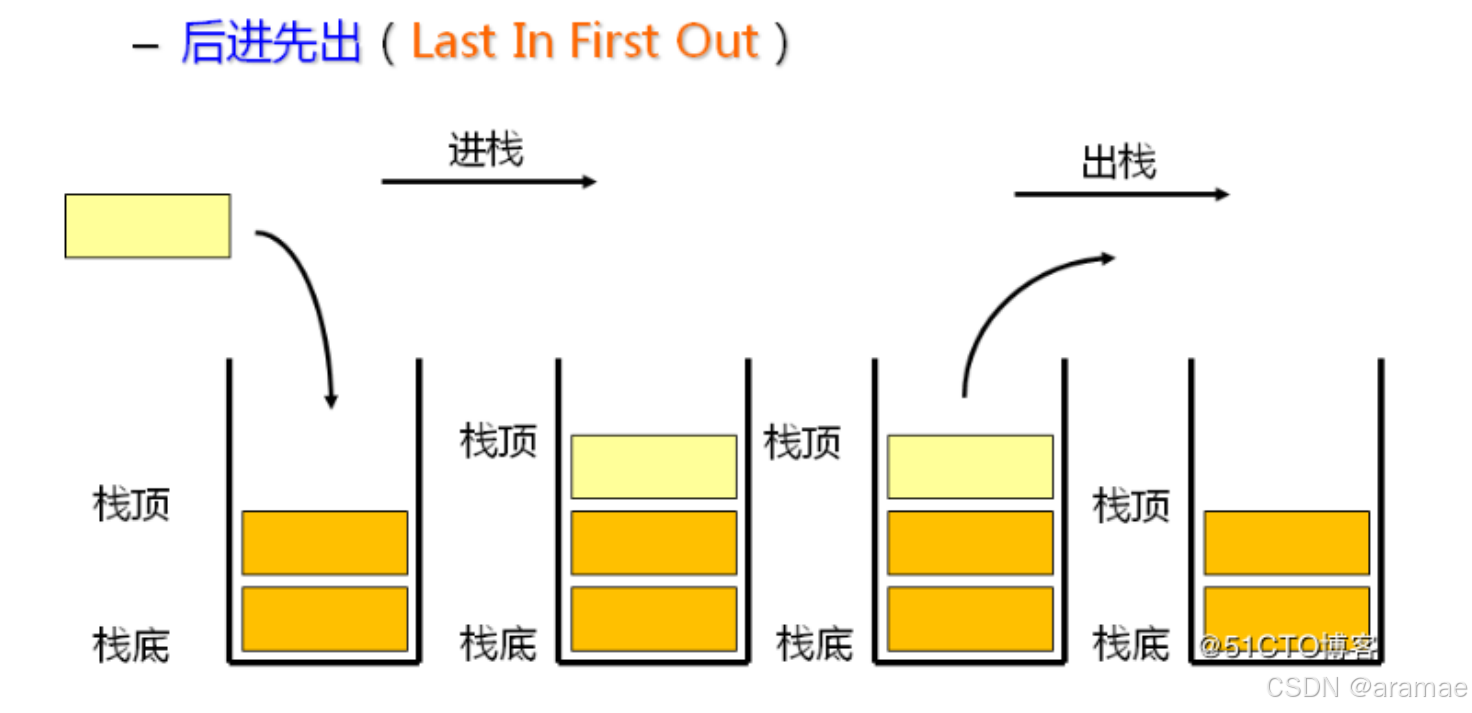
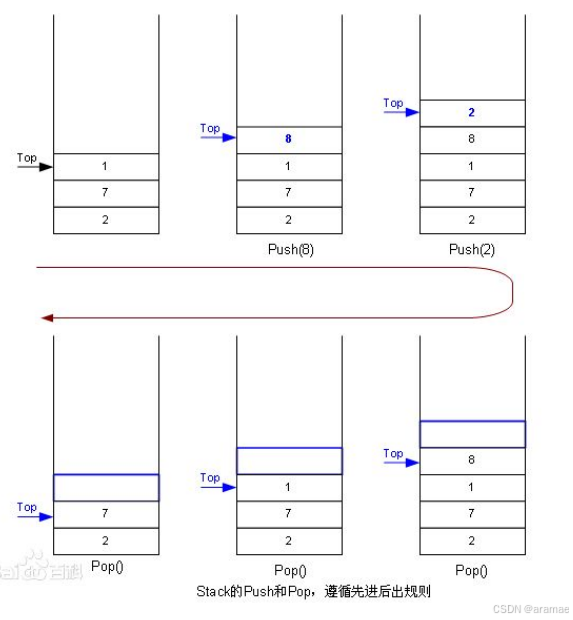
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端 称为栈顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

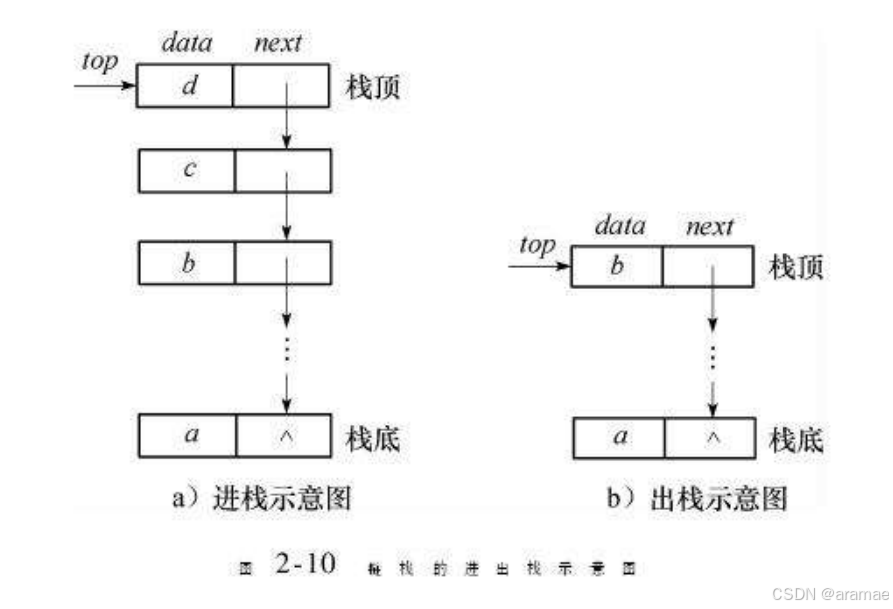
2.栈的实现

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小

// 下面是定长的静态栈的结构，实际中一般不实用，
所以我们主要实现下面的支持动态增长的栈
typedef int STDataType;
#define N 10
typedef struct Stack
{STDataType _a[N];int _top; // 栈顶
}Stack;

下面是完整的动态栈的实现：

 #include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
//基本操作： 
// 1.初始化
// 2.销毁
// 3.判空
// 4.压栈
// 5.出栈
// 6.返回栈顶元素
// 7.返回栈中元素个数 //用顺序表实现栈
//栈的性质：后进先出 typedef int STDataType;typedef struct stack{STDataType* a;//指向栈底位置        int top;//已有栈顶元素的个数           int capacity;// 栈容量           }ST;//栈的初始化-- 和顺序表的一系列操作差不多 
void STInit(ST* ps)
{assert(ps); ps->a = (STDataType*)malloc(sizeof(STDataType)*4);if(ps->a == NULL){perror("malloc fail");return;} ps->capacity = 4;//初始化容量为4 ，不够再扩容//ps->top = 0;//top是栈顶元素下一个 ps->top = -1;//top是栈顶元素 }//栈的销毁 
void STDestroy(ST* ps)
{assert(ps);free(ps->a);ps->a=NULL;ps->top=ps->capacity = 0;}//判空 
bool STEmpty(ST* ps)
{assert(ps);return ps->a[ps->top] == 0;
}void STPush(ST* ps, STDataType x)
{assert(ps);if(ps->top + 1 == ps->capacity){STDataType* tmp = (STDataType*)realloc(ps->a,sizeof(STDataType)*ps->capacity*2);if(tmp == NULL){perror("realloc fail");return;}ps->a = tmp;ps->capacity *= 2; }ps->a[ps->top+1] = x;ps->top++;
}//出栈 
void STPop(ST* ps)
{assert(ps);assert(!STEmpty(ps));ps->top--;}//栈中元素个数 
int STSize(ST* ps)
{assert(ps);return ps->top+1;
}//栈顶元素 
STDataType STTop(ST* ps)
{assert(ps);assert(!STEmpty(ps));	return ps->a[ps->top];
}int main()
{ST st;STInit(&st);//初始化//压栈-- 向栈中放入数据STPush(&st,1); STPush(&st,2); STPush(&st,3); STPush(&st,4); STPush(&st,5); //取栈顶元素//根据栈的性质  top == 5 // 打印出来看一下printf("%d\n",STTop(&st));//出栈--弹出栈顶元素STPop(&st);STPop(&st);//Pop两次 -- 那么此时栈顶的元素应该为 3//打印出来看一下printf("%d\n",STTop(&st));STPop(&st);//此时栈中应该只有两个元素了//打印栈中元素的个数printf("%d\n",STSize(&st));//最终结果为 5 //           3//			   2 //销毁栈STDestroy(&st);//以上为一个栈从创建到销毁的完整的过程//能够完成栈的基本操作 return 0;}

二. 队列

1.队列的概念及结构

队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出 FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾出队列：进行删除操作的一端称为队头

2. 动态链式队列的实现

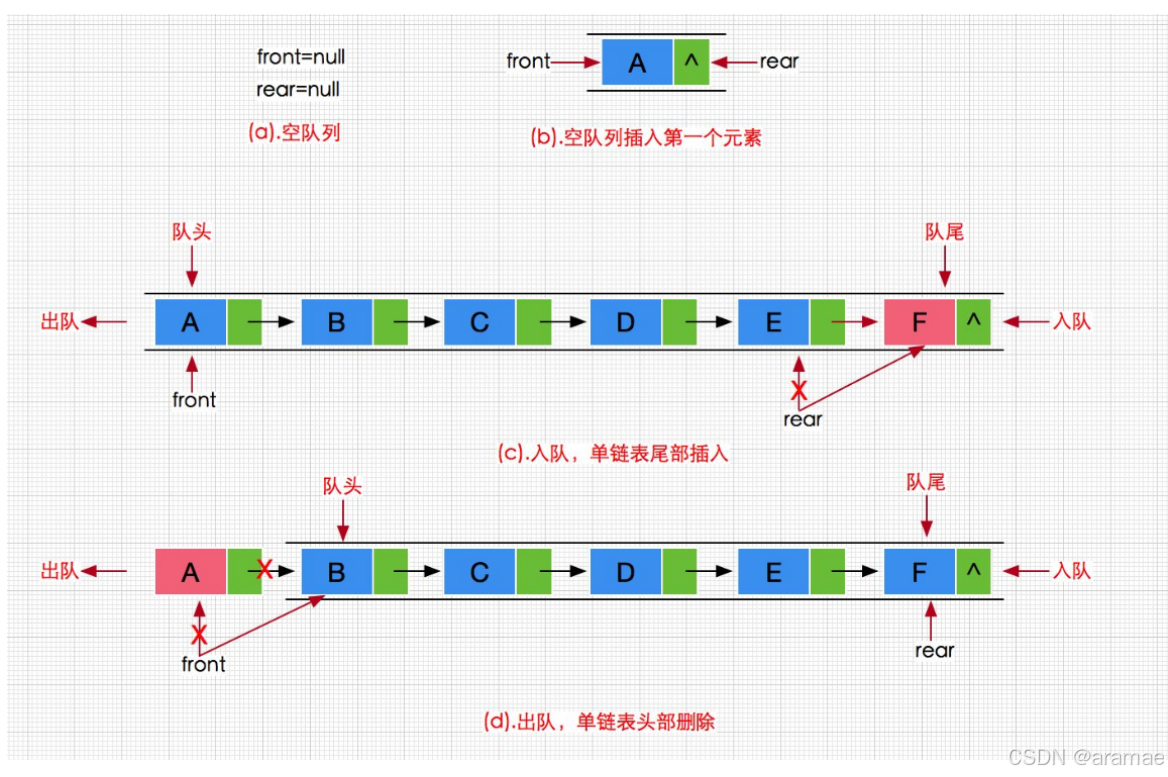
队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

下面实现一个动态队列（链表）

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
//队列性质：先进先出 ///*  1.队列初始化2.队列销毁3. 入对列4.出队列5.判空6.返回队列长度 7.返回队头数据8.返回队尾数据 
*/
//用单链表实现队列 
//使用两个结构体
//一个表示链表的节点的构成    
//一个用来描述队列 
typedef int  QDatatype;//队列的节点 
typedef struct QueueNode
{struct QueueNode* next;QDatatype data;
}QNode;//描述队列 
typedef struct Queue
{QNode* head;//队头位置 QNode* tail;//队尾位置 int size;//队列长度 
}Queue;//判空 
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0; 
}//初始化 
void QueueInit(Queue* pq)
{assert(pq);pq->head = NULL;pq->tail = NULL;pq->size = 0;
}//销毁队列 
void QueueDestroy(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));QNode* cur = pq->head;while(cur){QNode* next = cur->next;free(cur);cur = NULL;cur = next; } pq->head = pq->tail = NULL;pq->size = 0; }//入队列 
void QueuePush(Queue* pq, QDatatype x)
{//创建新的节点 QNode* newnode =(QNode*)malloc(sizeof(QNode));if(newnode == NULL){perror("malloc fail");return ;} newnode->data = x;newnode->next = NULL;if(pq->head==NULL){assert(pq->tail == NULL);pq->head = pq->tail = newnode; }else{pq->tail->next = newnode;pq->tail = newnode;}pq->size++; 
}//出队列 
void QueuePop(Queue* pq)
{assert(pq);assert(pq->head!=NULL);if(pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL; }else{QNode* next = pq->head->next;free(pq->head);pq->head = next;}pq->size--;} //返回队列长度 
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}//返回队头数据 
QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;}//返回队尾数据 
QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->tail->data;
}//打印队列 
void QueuePrint(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));QNode* cur = pq->head;while(cur){QNode* next = cur->next;printf("%d  ",cur->data);cur =next;}}int  main()
{Queue pq;//定义一个队列//下面来实现一下队列的基本功能 //1.初始化QueueInit(&pq);//2.向队列中放入数据//这里试放8个QueuePush(&pq, 1);//打印出来看一下 //1printf("%d\n", QueueFront(&pq)); //继续放 QueuePush(&pq, 2);QueuePush(&pq, 3);QueuePush(&pq, 4);QueuePush(&pq, 5);QueuePush(&pq, 6);QueuePush(&pq, 7);QueuePush(&pq, 8);//这里我们可以再添加一个函数，用来打印整个对列//便于我们观察整个队列的变化 QueuePrint(&pq); printf("\n");//3.出队列 ，这里选择出四个数据 QueuePop(&pq);QueuePop(&pq);QueuePop(&pq);QueuePop(&pq);//再观察队列里的数据QueuePrint(&pq);printf("\n");QueuePop(&pq);//观察此时 队头，队尾数据和队列长度// 6 8 3printf("%d  ",QueueFront(&pq));printf("%d  ",QueueBack(&pq));	   printf("%d  ",QueueSize(&pq));	   return 0;}

3. 静态顺序队列实现（一般教学使用）

静态顺序队列的使用不多，一般会在教学时进行使用示范；不做过多讲解，看一下就行；

这里动态的顺序队列就不再给出了。

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>// 队列性质：先进先出
/*  1.队列初始化2.队列销毁3.入队列4.出队列5.判空6.判满7.返回队列长度 8.返回队头数据9.返回队尾数据 
*/#define MAX_SIZE 100  // 队列最大容量typedef int QDatatype;// 非循环顺序队列结构
typedef struct Queue
{QDatatype data[MAX_SIZE];  // 存储队列元素的数组int front;                 // 队头指针int rear;                  // 队尾指针
}Queue;// 初始化队列
void QueueInit(Queue* pq)
{assert(pq);pq->front = 0;pq->rear = 0;
}// 销毁队列
void QueueDestroy(Queue* pq)
{assert(pq);pq->front = 0;pq->rear = 0;
}// 判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->front == pq->rear;
}// 判满
bool QueueFull(Queue* pq)
{assert(pq);return pq->rear == MAX_SIZE;
}// 入队列
void QueuePush(Queue* pq, QDatatype x)
{assert(pq);if(QueueFull(pq)){printf("Queue is full!\n");return;}pq->data[pq->rear] = x;pq->rear++;  // 简单递增，不循环
}// 出队列
void QueuePop(Queue* pq)
{assert(pq);if(QueueEmpty(pq)){printf("Queue is empty!\n");return;}pq->front++;  // 简单递增，不循环
}// 返回队列长度
int QueueSize(Queue* pq)
{assert(pq);return pq->rear - pq->front;
}// 返回队头数据
QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->data[pq->front];
}// 返回队尾数据
QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->data[pq->rear - 1];
}// 打印队列
void QueuePrint(Queue* pq)
{assert(pq);if(QueueEmpty(pq)){printf("Queue is empty!\n");return;}for(int i = pq->front; i < pq->rear; i++){printf("%d  ", pq->data[i]);}printf("\n");
}// 重置队列（当队列出现假溢出时使用）
void QueueReset(Queue* pq)
{assert(pq);if(pq->front == 0) {printf("Cannot reset: front is already at 0\n");return;}// 将剩余元素前移int size = QueueSize(pq);for(int i = 0; i < size; i++){pq->data[i] = pq->data[pq->front + i];}pq->front = 0;pq->rear = size;printf("Queue reset completed. New size: %d\n", size);
}int main()
{Queue pq;  // 定义一个非循环顺序队列// 1.初始化QueueInit(&pq);// 2.向队列中放入数据printf("Pushing elements into the queue:\n");for(int i = 1; i <= 5; i++){QueuePush(&pq, i);printf("Pushed %d, Front: %d, Rear: %d, Size: %d\n", i, pq.front, pq.rear, QueueSize(&pq));}printf("Queue elements: ");QueuePrint(&pq);// 3.出队列printf("\nPopping elements from the queue:\n");for(int i = 0; i < 3; i++){printf("Before pop - Front: %d, Rear: %d, Size: %d\n", pq.front, pq.rear, QueueSize(&pq));QueuePop(&pq);printf("After pop - Front: %d, Rear: %d, Size: %d\n", pq.front, pq.rear, QueueSize(&pq));}printf("Queue elements after popping: ");QueuePrint(&pq);// 4.演示假溢出问题printf("\nDemonstrating false overflow:\n");// 现在队列前面有空位，但继续添加元素直到rear到达MAX_SIZEint initialSize = QueueSize(&pq);int availableSpace = MAX_SIZE - pq.rear;printf("Current state - Front: %d, Rear: %d, Size: %d\n", pq.front, pq.rear, QueueSize(&pq));printf("Available space at the end: %d\n", availableSpace);// 添加元素直到rear达到MAX_SIZEfor(int i = 1; i <= availableSpace; i++){QueuePush(&pq, i * 10);}printf("After filling available space - Front: %d, Rear: %d, Size: %d\n", pq.front, pq.rear, QueueSize(&pq));// 尝试再添加一个元素 - 会出现假溢出printf("Trying to push one more element:\n");QueuePush(&pq, 999);// 5.重置队列解决假溢出printf("\nResetting queue to solve false overflow:\n");QueueReset(&pq);printf("After reset - Front: %d, Rear: %d, Size: %d\n", pq.front, pq.rear, QueueSize(&pq));// 现在可以继续添加元素printf("Now we can push more elements:\n");QueuePush(&pq, 100);QueuePush(&pq, 200);printf("Final queue: ");QueuePrint(&pq);printf("Front: %d, Rear: %d, Size: %d\n", pq.front, pq.rear, QueueSize(&pq));return 0;
}

3.5 非循环顺序队列的缺点

非循环顺序队列虽然实现简单，但在实际应用中存在许多严重缺点，这也是为什么循环队列更常用的原因

3.5.1 假溢出（False Overflow）

这是最严重的缺点

假溢出的根本原因

问题根源：

顺序队列的指针只能单向移动

rear指针到达数组末尾后无法"回头"

即使数组前部有空闲位置，也无法利用

数学表达：

可用空间 = (front位置的空闲) + (MAX_SIZE - rear)

但由于指针移动规则限制，这些空间实际上无法使用

// 示例场景
#define MAX_SIZE 5
Queue pq;
QueueInit(&pq);// 入队5个元素
QueuePush(&pq, 1);  // front=0, rear=1
QueuePush(&pq, 2);  // front=0, rear=2
QueuePush(&pq, 3);  // front=0, rear=3
QueuePush(&pq, 4);  // front=0, rear=4
QueuePush(&pq, 5);  // front=0, rear=5 (队列满)// 出队3个元素
QueuePop(&pq);  // front=1, rear=5
QueuePop(&pq);  // front=2, rear=5  
QueuePop(&pq);  // front=3, rear=5// 现在队列状态：
// data[0]=1, data[1]=2, data[2]=3, data[3]=4, data[4]=5
// front=3, rear=5, size=2
// 实际只有2个元素，但无法继续入队！

问题分析：虽然数组中还有3个空位（索引0,1,2），但 rear 已经到达末尾新元素无法插入，即使数组前面有空闲空间这被称为"假溢出"，因为队列实际上并没有真正满

那么或许有人会问：链表实现的队列会有假溢出风险吗？ 答案是不会

链表实现的队列没有假溢出问题，因为：

动态内存分配：每个节点独立分配，不受固定边界限制

无位置约束：新节点可以随时创建并链接到队尾

真正的按需使用：用多少内存就分配多少，不会出现"有空间但不能用"的情况

链表队列只有在系统内存真正耗尽时才会出现溢出，这种情况属于真溢出，而不是假溢出

3.5.2 空间利用率低


// 最坏情况下，队列只能使用一次
// 即使频繁出队入队，数组前面的空间也无法重用
// 空间利用率 = (rear - front) / MAX_SIZE// 示例：MAX_SIZE=100
// 入队100个，出队99个，再入队1个 → 空间利用率只有1%
// 但实际无法再入队，因为rear=100
空间浪费表现：随着操作的进行，可用空间逐渐减少即使队列中元素很少，也可能无法添加新元素需要定期重置来回收空间

非循环顺序队列的主要缺点集中在假溢出导致的低空间利用率和重置操作带来的性能问题。这些缺点使得它在实际应用中很少被采用，循环队列通过简单的取模运算就完美解决了这些问题，成为更实用的选择。

除非有特殊的约束条件要求使用非循环实现，否则在大多数情况下都应该选择循环队列

（下面介绍一下循环队列）

4. 循环队列

循环队列的概念

循环队列是为了解决普通队列在数组实现中"假溢出"问题而设计的。通过将数组视为一个环形结构，可以重复利用出队后释放的空间。

循环队列可以是静态的也可以是动态的。静态循环队列容量固定，动态循环队列可以在运行时扩容。选择静态还是动态取决于应用场景：

如果能够确定队列的最大容量，且内存有限，可以使用静态循环队列。
如果队列大小不确定，或者需要处理大量数据，动态循环队列更合适。

在实际应用中，动态循环队列更灵活，但静态循环队列在嵌入式系统等资源受限的环境中可能更常用

循环队列实现（静态）

#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>// 队列性质：先进先出
/*  1.队列初始化2.队列销毁3.入队列4.出队列5.判空6.判满7.返回队列长度 8.返回队头数据9.返回队尾数据 
*/#define MAX_SIZE 100  // 队列最大容量typedef int QDatatype;// 静态顺序队列结构
typedef struct Queue
{QDatatype data[MAX_SIZE];  // 存储队列元素的数组int front;                 // 队头指针int rear;                  // 队尾指针int size;                  // 队列当前长度
}Queue;// 初始化队列
void QueueInit(Queue* pq)
{assert(pq);pq->front = 0;pq->rear = 0;pq->size = 0;
}// 销毁队列（静态队列无需特殊销毁操作）
void QueueDestroy(Queue* pq)
{assert(pq);pq->front = 0;pq->rear = 0;pq->size = 0;
}// 判空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->size == 0;
}// 判满
bool QueueFull(Queue* pq)
{assert(pq);return pq->size == MAX_SIZE;
}// 入队列
void QueuePush(Queue* pq, QDatatype x)
{assert(pq);if(QueueFull(pq)){printf("Queue is full!\n");return;}pq->data[pq->rear] = x;pq->rear = (pq->rear + 1) % MAX_SIZE;  // 循环队列pq->size++;
}// 出队列
void QueuePop(Queue* pq)
{assert(pq);if(QueueEmpty(pq)){printf("Queue is empty!\n");return;}pq->front = (pq->front + 1) % MAX_SIZE;  // 循环队列pq->size--;
}// 返回队列长度
int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}// 返回队头数据
QDatatype QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->data[pq->front];
}// 返回队尾数据
QDatatype QueueBack(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));// rear指向的是下一个插入位置，所以队尾元素在rear-1位置int lastIndex = (pq->rear - 1 + MAX_SIZE) % MAX_SIZE;return pq->data[lastIndex];
}// 打印队列
void QueuePrint(Queue* pq)
{assert(pq);if(QueueEmpty(pq)){printf("Queue is empty!\n");return;}int current = pq->front;for(int i = 0; i < pq->size; i++){printf("%d  ", pq->data[current]);current = (current + 1) % MAX_SIZE;}printf("\n");
}int main()
{Queue pq;  // 定义一个静态顺序队列// 1.初始化QueueInit(&pq);// 2.向队列中放入数据QueuePush(&pq, 1);printf("Front element: %d\n", QueueFront(&pq));// 继续放入数据QueuePush(&pq, 2);QueuePush(&pq, 3);QueuePush(&pq, 4);QueuePush(&pq, 5);QueuePush(&pq, 6);QueuePush(&pq, 7);QueuePush(&pq, 8);printf("Queue elements: ");QueuePrint(&pq);// 3.出队列QueuePop(&pq);QueuePop(&pq);QueuePop(&pq);QueuePop(&pq);printf("After popping 4 elements: ");QueuePrint(&pq);QueuePop(&pq);// 观察此时队头、队尾数据和队列长度printf("Front: %d  ", QueueFront(&pq));printf("Back: %d  ", QueueBack(&pq));printf("Size: %d\n", QueueSize(&pq));// 测试队列满的情况printf("\nTesting queue full scenario:\n");QueueDestroy(&pq);  // 重置队列QueueInit(&pq);// 填满队列for(int i = 0; i < MAX_SIZE; i++){QueuePush(&pq, i + 1);}printf("Queue size when full: %d\n", QueueSize(&pq));printf("Is queue full? %s\n", QueueFull(&pq) ? "Yes" : "No");// 尝试在满队列中插入QueuePush(&pq, 999);  // 应该显示队列已满return 0;
}

🔄 核心机制：循环指针

// 关键代码：循环移动
pq->rear = (pq->rear + 1) % MAX_SIZE;  // 入队
pq->front = (pq->front + 1) % MAX_SIZE; // 出队
工作原理：
• 当指针到达数组末尾时，通过取模运算回到数组开头
• 形成逻辑上的"环形"结构，物理上仍是线性数组
• 实现空间的循环复用

初始: [][][][][]   front=0, rear=0
入队A: [A][][][][]  front=0, rear=1
入队B: [A][B][][][] front=0, rear=2
出队A: [][B][][][]  front=1, rear=2
入队C: [][B][C][][] front=1, rear=3
入队D: [][B][C][D] front=1, rear=4
入队E: [E][B][C][D] front=1, rear=0 ← 循环到开头！

入队：rear = (rear + 1) % MAX_SIZE

出队：front = (front + 1) % MAX_SIZE

解决"假溢出"问题，充分利用空间

三. 队列小结

推荐使用静态循环队列（嵌入式），链式队列（开发友好）；

四. 栈 vs 队列：对比总结

特性	栈	队列
操作原则	LIFO（后进先出）	FIFO（先进先出）
插入操作	push（压栈）	enqueue（入队）
删除操作	pop（弹栈）	dequeue（出队）
查看操作	peek（查看栈顶）	front（查看队头）
典型应用	函数调用、括号匹配、撤销操作	任务调度、BFS、消息队列
实现难度	相对简单	需要处理循环或链表

关键要点与选择

选择依据：

需要 “回溯”、“撤销” 或 “嵌套” 结构？ → 用栈。

需要 “公平”、“按序处理” 或 “缓冲” ？ → 用队列。

实现方式：

两者都可以用数组或链表实现。

栈的实现相对简单。

队列的数组实现需要注意假溢出问题，通常使用循环队列来解决。

相互实现：

可以用两个栈实现一个队列。

可以用两个队列实现一个栈。

这充分体现了它们作为基础数据结构的灵活性和重要性。