当前位置：首页 > news >正文

合肥市高新区2025年初中信息学竞赛试题T1-T4 C++ 有故事听[doge]

news 2025/10/19 8:01:27

T1花的照片（photo）

【题目描述】

秋天到了，校园里开满了五颜六色的花朵。八年级2班的花园中也不例外。假设在八年级2班的花园中共有N朵花，排列成一行（1<=N<=100）。其中，第i朵花具有pi朵花瓣，（1<=pi<=100），小明作为班级的宣传委员，为了美化班级的电子板报，决定给这些花拍些照片。为了更好地选择更美丽的花朵，小明决定多拍一些照片，具体地说，对于每一对满足1<=i<=j<=N的花（i，j），小明都会给从花i到花j之间的所有花（包括i和j）拍一张合影。

后来小明查看这些照片选择花朵时注意到有些照片里存在着“平均”的花：一朵恰好有等于照片中所有花的花瓣数量的平均值的花。

请问：小明所拍的照片中有几张存在平均的花？

【输入格式】

共2行，其中，输入的第1行为花的总数N。第2行为每朵花具有的花瓣数目。

【输出格式】

输出存在平均的花的照片数量

【样例输入】

1 1 2 3

【样例输出】

【样例解释】

每张仅包含一朵花的照片均会被计入答案（在这个样例中有4张）。另外，在这个样例中i,j为（1,2）和（2,4）所对应的照片也存在平均的花。

【数据范围】

对于100%的数据，1<=N<=100,1<=pi<=100

/*T1三重循环朴素写法
没啥好说的 但我一直在是
*/
#include<bits/stdc++.h>
using namespace std;
int a[105],ans;
int main(){freopen("photo.in","r",stdin);freopen("photo.out","w",stdout);int n;cin>>n;for(int i=1; i<=n; i++){cin>>a[i];}for(int i=1; i<=n; i++){int sum=0;for(int j=i; j<=n; j++){sum+=a[j];double avg=sum*1.0/(j-i+1);int flag=0;for(int y=i; y<=j; y++){if(a[y]==avg){ans++;flag=1;break;}}}}cout<<ans;return 0;
}
/*T1判断整除性优化
其实可以再用前缀和+哈希表优化
*/
#include<bits/stdc++.h>
using namespace std;
int a[105],ans,b[10005];
int main(){freopen("photo.in","r",stdin);freopen("photo.out","w",stdout);int n;cin>>n;for(int i=1; i<=n; i++){cin>>a[i];}for(int i=1; i<=n; i++){int sum=0;for(int j=i; j<=n; j++){sum+=a[j];int len=j-i+1;if(sum%len==0){int avg=sum/len;for(int k=i; k<=j; k++){if(a[k]==avg){ans++;break;}}}}}cout<<ans;return 0;
}

T2地图编辑器（edit）

【题目描述】

你正在实现一款简易的地图编辑器软件。在这款简易地图编辑器中，树的形状只有一种，如下图所示，其中X为树的图块，.为透明图块，第5行第3列为树根：

..X..

.XXX.

XXXXX

..X..

新建一张n*m的地图时，所有格子都是空地，优先级为0，空地也用.表示。地图由n*m个格子组成，从上到下依次为1,2……n行，从左到右依次为第1,2……m列。接下来，用户将往地图上放置k（1<=k<=9）棵树。第i（1<=i<=k）次放置操作，用户将选中地图内的格子（xi,yi ），将其作为第i棵树的树根的位置，这棵树所有非透明图块均用数字i表示，优先级均为xi。

你的任务是根据放置信息绘制出地图，每个位置仅需要展示优先级最高的图块，并请忽略所有超出地图范围的图块。

【输入格式】

第一行包含三个正整数n、m、k（1 ≤ n, m ≤ 10，1 ≤ k ≤ 9），分别表示地图的尺寸以及树的数量。接下来k行，每行两个正整数xi、yi（1 ≤ i ≤ n，1 ≤ yi ≤ m），依次表示每棵树的位置。

输入数据保证不会有两棵树位于同一行。

【输出格式】

输出n行，每行一个长度为m的字符串，从上到下表示地图。

【输入样例】

7 7 3

4 5

6 4

3 1

【输出样例】

333111.

3.12111

3.222..

.22222.

...2...

.......

【数据范围】

对于10%的数据，n = 1，m = 1，k = 1。

对于30%的数据，m = 1，k = 1。

对于50%的数据，k = 1。

对于100%的数据，1 ≤ n, m ≤ 10，1 ≤ k ≤ 9。

/*T2
在图中填充树（替换“.”成树的下标ki） but注意边界
树的样式
..X..
.XXX.
XXXXX
..X..
..X..X表示第几棵树
*/
//1)数组模拟 朴素好用
#include<bits/stdc++.h>
#define ch a<=n&&a>=1&&b>=1&&b<=m
using namespace std;
char c[15][15];
int main(){int n,m,k;freopen("edit.in","r",stdin);freopen("edit.out","w",stdout);cin>>n>>m>>k;for(int i=1; i<=n; i++){for(int j=1; j<=m; j++){c[i][j]='.';}}for(int i=1; i<=k; i++){int x,y;cin>>x>>y;int a=x,b=y;if(ch){c[a][b]=i+'0';}a-=1;if(ch){c[a][b]=i+'0';}a-=1;if(ch){int t=b-2,p=b+2;while(!(t>=0&&t<=m)){t++;}while(!(p>=0&&p<=m)){p--;}for(int j=t; j<=p; j++){c[a][j]=i+'0';}}a-=1;if(ch&&b-1>=1&&b+1<=m){int t=b-1,p=b+1;while(!(t>=0&&t<=m)){t++;}while(!(p>=0&&p<=m)){p--;}for(int j=t; j<=p; j++){c[a][j]=i+'0';}}a-=1;if(ch){c[a][b]=i+'0';}}for(int i=1 ;i<=n; i++){for(int j=1; j<=m; j++){cout<<c[i][j];}cout<<endl;}
}
//2)高级数组模拟[doge]
#include<bits/stdc++.h>
using namespace std;
char c[15][15];
int n,m,k;
struct Tree{int dx[5]={0,-1,-2,-3,-4};  //树的5行相对行偏移int len[5]={1,1,5,3,1};     //每行X的数量int st[5]={0,0,-2,-1,0};    //每行起始列偏移
};
bool check(int a,int b){return a>=1&&a<=n&&b>=1&&b<=m;
}
int main(){freopen("edit.in","r",stdin);freopen("edit.out","w",stdout);cin>>n>>m>>k;Tree t;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)c[i][j]='.';for(int ki=1;ki<=k;ki++){int x,y;cin>>x>>y;for(int i=0;i<5;i++){int a=x+t.dx[i];if(a<1||a>n) continue;int l=y+t.st[i],r=l+t.len[i]-1;l=max(1,l); r=min(m,r);	for(int j=l;j<=r;j++){if(check(a,j)){c[a][j]=ki+'0';}}}}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cout<<c[i][j];}cout<<endl;}return 0;
}

T3回文游戏（palindrome）

【题目描述】

小明和小红正在使用一堆初始时共N个石子（1<=N<1010000）进行一个游戏。规定两人依次行动。

游戏规则是：当轮到某人行动时，他必须从堆中取走x个石子，其中x是该人选定的任意正整数回文数。如果当某人的回合开始时石子堆是空的，那么这个人就输了。

正整数回文数定义：一个正整数如果从前向后和从后向前读相同，则该数为回文数；回文数的例子有1、121和9009等。回文数不允许有前导零；例如，990不是回文数。

小明先行动。

有T（1<=T<=10）个独立的测试用例。对于每一个测试用例，输出如果两人都采取最优策略，谁会赢得游戏。

【输入格式】

输入的第1行包含T，即测试用例的数量。以下T行为测试用例，每个测试用1行。

每个测试用例均由一个整数N指定。

输出格式：

对于每一个测试用例输出一行，如果小明在最优策略下可以从一堆N个石子的石子堆开始赢得游戏则输出B，否则输出E。

【样例输入】

【样例输出】

【样例解释】

对于第一个测试用例，小明可以在第一次行动中取走所有石子，因为8是回文数，使他获胜。对于第二个测试用例，不是回文数，因此小明无法在第一次行动中取走所有石子。无论小明第一回合取走多少石子，小红总能在第二回合取走所有余下的石子，使她获胜。对于第三个测试用例，可以证明在最优策略下小明可以获胜。

【数据范围】

对于10%的数据，N<100；

对于40%的数据，N<10^6 ；

对于70%的数据，N<10^9；

对于100%的数据，N<10^10000。

/*T3正解（外校九年级大佬写的）
回文的数学规律 数字中1的个数和数字长度的奇偶性决定最终胜负
*/
#include <bits/stdc++.h>
using namespace std;bool check(string s){int l=0,r=s.size()-1;while(l<r){if(s[l]!=s[r]) return 0;l++; r--;}return 1;
}int main(){int T;cin>>T;while(T--){string n;cin>>n;int flag=0;for(int i=0;i<n.size();i++){if(n[i]!='0'){flag=1;break;}}if(!flag){cout<<"E"<<endl;continue;}if(n=="1"){cout<<"B"<<endl;continue;}int cnt=0;for(int i=0;i<n.size();i++){if(n[i]=='1') cnt++;}if(cnt==1){int sum=0;for(int i=0;i<n.size();i++){sum+=n[i]-'0';}if(sum==1){cout<<"B"<<endl;}else{if((n.size()-1)%2==1) cout<<"B"<<endl;else cout<<"E"<<endl;}}else{if(n.size()%2==1) cout<<"B"<<endl;else cout<<"E"<<endl;}}return 0;
}
/*T3 DFS(写一半没思路了 去写BFS了 结果就是时间完全不够用 现在尝试补全)
每次递归时 尝试所有可能的回文数取法（从1位到整个数字长度）
如果某种取法能让对手处于必败状态 则当前玩家获胜 
基础情况是当数字为0时当前玩家输 数字为1时可以直接取完获胜
*/
#include <bits/stdc++.h>
using namespace std;bool check(string s){int l=0,r=s.size()-1;while(l<r){if(s[l]!=s[r]) return 0;l++; r--;}return 1;
}bool dfs(string n){if(n=="0") return 0;if(n=="1") return 1;int len=n.size();int flag=0;for(int i=0;i<len;i++){if(n[i]!='0'){flag=1;break;}}if(!flag) return 0;for(int i=1;i<=len;i++){string tmp="";for(int j=0;j<i;j++){tmp+=n[j];}if(!check(tmp)) continue;string next_n="";int st=0;while(st<len&&n[st]=='0') st++;for(int j=st;j<len;j++){if(j>=i) next_n+=n[j];}if(next_n=="") next_n="0";if(!dfs(next_n)) return 1;}return 0;
}int main(){int T;cin>>T;while(T--){string n;cin>>n;if(dfs(n)) cout<<"B"<<endl;else cout<<"E"<<endl;}return 0;
}
/*T3 BFS（有点像博弈论 能走到必败态的状态是必胜态 所有后继都是必胜态的状态是必败态 听他们说也可以叫拓扑排序） but空间爆炸*/
#include <bits/stdc++.h>
using namespace std;bool check(const string& s) {int l = 0, r = s.size() - 1;while (l < r) {if (s[l] != s[r]) return 0;l++; r--;}return 1;
}int main() {int T;cin >> T;while (T--) {string n;cin >> n;if (n == "0") {cout << "E" << endl;continue;}if (n == "1") {cout << "B" << endl;continue;}map<string, int> vis;queue<string> q;vis["0"] = -1;q.push("0");vis["1"] = 1;q.push("1");int cnt = 0; while (!q.empty()) {string cur = q.front();q.pop();cnt++;if (cnt % 1000 == 0) {cout << "debug" << cnt << " " << cur << endl;}int cur_state = vis[cur];int cur_len = cur.size();for (int i = cur_len; i <= n.size(); i++) {for (int j = 0; j < 10; j++) {// 这里会产生大量重复和无效状态 bfs超级拉胯string next = cur;while (next.size() < i) next = "0" + next;for (int k = 0; k <= 9; k++) {string candidate = to_string(k) + next;if (candidate.size() > n.size()) continue;if (candidate.size() == n.size() && candidate > n) continue;if (!check(candidate)) continue;
//						// （调试）输出新生成的状态
//						if (cnt < 100) {
//							cout << "Debug" << candidate << " from " << cur << endl;
//						}if (vis.find(candidate) == vis.end()) {if (cur_state == -1) {vis[candidate] = 1;q.push(candidate);} else {vis[candidate] = -1; q.push(candidate);}}}}}
//			if (cnt > 100000) {
//				cout << "WTF" << endl;
//				break;
//			}}if (vis.find(n) != vis.end() && vis[n] == 1) {cout << "B" << endl;} else {cout << "E" << endl;}}return 0;
}

T4四柱汉诺塔（hanoif）

【题目描述】

小明和小红在一起玩汉诺塔游戏，汉诺塔一共有3根柱子，其中，在第一个柱子上有n个直径不同的盘子，越往上盘子直径越小。如图所示：

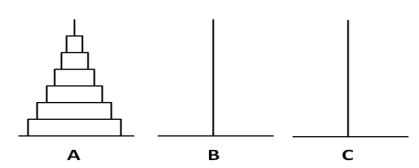
移动规则是：你每次只能移动一个盘子，同时必须时刻保证直径小的盘子位于直径大的盘子之上，看谁能够利用最少的移动次数把所有的盘子从A柱经B柱移动到C柱。

玩了一会以后，他们发现了一个有趣的现象，即最少的移动次数一定是2n-1，比如，如果一开始在A柱上有3个盘子，则最少需要移动7次才能完成游戏。

小明和小红是爱思考的孩子，他们想，如果我再多加一个柱子会怎么样呢？说干就干，于是他们就又加上了一个柱子，变成了4柱汉诺塔，即有A，B，C，D四个柱子，在A柱上有由小到大堆放的n个盘子，如图所示：

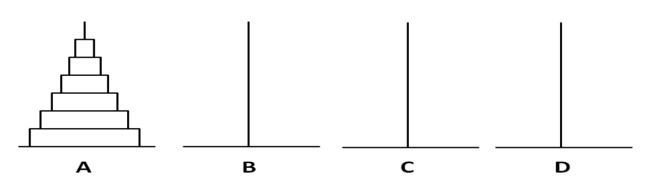
现在需要你将A柱上的盘子经B柱和C柱移动到D柱上去，移动的规则如下：

①每次只能移动一个盘子。

②在移动的过程中，小盘子只能放到大盘子的上面。

求将n个盘子由A柱移到D柱的最少移动次数。

请聪明的你来完成这个挑战。

【输入文件】

共一行：一个整数n（1<= n <=60），表示有n个盘子

【输出文件】

共一行：一个整数m，表示将n个盘子由A柱移到D柱的最少移动次数

【样例输入】

【样例输出】

【数据范围】

对于10%的数据，n<=10；

对于40%的数据，n<=20 ；

对于70%的数据，n<=30；

对于100%的数据，n<=60。

/*T4-1
Frame算法：将n个盘子视为上下两部分 通过枚举不同的分割方式 找到移动次数最少的方案。
递推公式：f[n] = min(2 * f[n-k] + (2^k - 1))
其中 f[n-k]是四柱模式下移动上部盘子的次数
(2^k - 1)是三柱模式下移动下部k个盘子的次数
*/
#include <bits/stdc++.h>
using namespace std;long long f[100],g[100];int main(){int n;cin>>n;memset(f,0x3f,sizeof(f));f[1]=1;g[1]=1;for(int i=2;i<=n;i++){for(int j=1;j<i;j++){f[i]=min(f[i],2*g[j]+(1LL<<(i-j))-1);}g[i]=f[i];}cout<<f[n];return 0;
}
/*T4-2
递归正解也基于Frame算法（+记忆化） 动规寻找最优分割点
h3(n)计算三柱汉诺塔移动次数（公式：2^n - 1）
h4(n)递归求解四柱问题：
将n个盘子分为上下两部分（上k个，下n-k个）
用四柱模式将上部k个移到辅助柱
用三柱模式将下部n-k个移到目标柱
用四柱模式将上部k个移到目标柱
循环 k from 1 to n-1寻找最优分割点
时间复杂度：O(n²)（使用记忆化避免重复计算）
*/
#include <bits/stdc++.h>
using namespace std;long long f[1005];long long h3(int n){if(n == 1) return 1;return 2 * h3(n-1) + 1;
}long long h4(int n){if(n == 1) return 1;if(n == 2) return 3;if(f[n]) return f[n];long long mn = 1e18;for(int k = 1; k < n; k++){long long t = 2 * h4(k) + h3(n-k);if(t < mn) mn = t;}return f[n] = mn;
}int main(){int n;cin >> n;cout << h4(n);return 0;
}

查看全文

http://www.dtcms.com/a/499393.html