【数论】最大公因数 (gcd) 与最小公倍数 (lcm)

一、最大公因数 (gcd)

1. 最大公因数的性质

我们在小学的时候就学过最大公因数 (Greatest Common Divisor, 简称 GCD)，就是两个或多个数所有公因数中最大的那一个。比如 $12$ 和 $18$ 的最大公因数是 $6$。我们通常把两个数 $x$ 和 $y$ 的最大公因数记为 $gcd(x,y)$ 或者 $(x,y)$。你也许学过短除法、辗转相除法来求最大公因数，但是如果落实到代码上，该如何写呢？首先我们需要了解最大公因数的几个性质：

对于任意整数 $a$，$b$，$c$，有

1. $(a,b)=(b,a)=(-a,b)=(a,-b)$；

2. 若 $a\mid b$（" $\mid$ " 为整除符号，意为 $b$ 能够被 $a$ 整除），则 $(a,b)=a$；

3. 对于任意两个整数 $x$，$y$，必有 $(a,b)\mid ax+by$；

4. 设 $x$ 是 $a$ 和 $b$ 的任意公因数，则有 $x\mid (a,b)$；

5. 若 $a=bq+c$，$q$ 是一个整数，则有 $(a,b)=(b,c)$。

其中第 5 个性质是我们用代码求解 gcd 的核心，下面对它进行证明：

证明：$(a,b)$ 是 $a$ 和 $b$ 的最大公因数，那么一定有
$$(a,b)\mid a$$
以及
$$(a,b)\mid b$$
因为 $a=bq+c$，所以 $c=a-bq$，又由性质 3 可知，两个数的最大公因数可以整除这两个数的线性组合，所以有
$$(a,b)\mid a-bq$$
即
$$(a,b)\mid c$$
由于 $(a,b)$ 既是 $b$ 的公因数，又是 $c$ 的公因数，所以 $(a,b)$ 是 $b$ 和 $c$ 的一个公因数，由性质 4 可得
$$(a,b)\mid (b,c)$$
同理可以用 $a=bq+c$ 求得
$$(b,c)\mid (a,b)$$
由于 $(a,b)$ 和 $(b,c)$ 相互整除，所以有
$$(a,b)=(b,c)$$
证毕。

---

2. 欧几里得算法

欧几里得算法，其实就是我们中学学过的辗转相除法，我们先来看一个例子：求 $(4864,3458)$。

我们先用 $4864$ 除以 $3458$，得到一个商和余数：
$$4864=3458\times 1+1406$$
由上面我们所证明的性质 5，$(4864,3458)$ 就转换成了求 $(3458,1406)$。

接着我们用 $3458$ 去除 $1406$，得到新的商和余数：
$$3458=1406\times 2+646$$
现在就转换成了求 $(1406,646)$。

像这样反复运算，我们的余数最终会变成 0，而我们所算出的最后一个非零余数就是最大公因数。这里的最后一个非零余数是 $38$，所以最大公因数是 $38$。

观察上面的计算过程我们不难发现，这中间的计算方法都是一样的，因此我们可以用递归来实现：

// 求两个数 x 和 y 的最大公因数
int gcd(int x, int y)
{if(y == 0) return x;return gcd(y, x % y);
}

---

二、最小公倍数 (lcm)

最小公倍数 (Least Common Multiple, 简称 LCM)，就是两个或多个数所有公倍数中最小的那个。比如 $8$ 和 $12$ 的最小公倍数是 $24$。我们通常把两个数 $x$ 和 $y$ 的最小公倍数记为 $lcm[x,y]$ 或者 $[x,y]$。

两个数的最小公倍数的求法十分简单，只需要计算出两个数的最大公因数 $(a,b)$，那么就有
$$[a,b]=\frac{a\times b}{(a,b)}$$

---

三、练习

1. 最大公因数和最小公倍数 ⭐

【题目链接】

B3634 最大公约数和最小公倍数 - 洛谷

【题目描述】

给定两个正整数 $a,b$，求他们的最大公约数（gcd）和最小公倍数（lcm）。这两个整数 $a,b$ 均在 int 范围内。

【输入格式】

两个整数 $a$ 和 $b$，用空格分隔。

【输出格式】

两个整数表示答案，用空格隔开。

【示例一】

输入

6 15

输出

3 30

#include<iostream>using namespace std;typedef long long LL;// 将 a 和 b 的类型设置为 long long 防止溢出
LL gcd(LL a, LL b)
{return b == 0 ? a : gcd(b, a % b);
}int main()
{LL a, b;cin >> a >> b;LL g = gcd(a, b);cout << g << ' ' <<  a * b / g << endl;return 0;
}

---

2. 三个数的最大公因数 ⭐

【题目链接】

[B3736 信息与未来 2018] 最大公约数 - 洛谷

【题目描述】

输入三个正整数 $x,y,z$，求它们的最大公约数（Greatest Common Divisor）$g$：最大的正整数 $g\ge 1$，满足 $x,y,z$ 都是 $g$ 的倍数，即 $(x\mathrm{mod}g)=(y\mathrm{mod}g)=(z\mathrm{mod}g)=0$。

【输入格式】

输入一行三个正整数 $x,y,z$。

【输出格式】

输出一行一个整数 $g$，表示 $x,y,z$ 的最大公约数。

【示例一】

输入

12 34 56

输出

2

【示例二】

输入

28 70 28

输出

14

【说明/提示】

样例 $1$

$12=2\times 6,34=2\times 17,56=2\times 28,g=2$。

样例 $2$

$28=14\times 2,70=14\times 5,28=14\times 2,g=14$。

数据规模

所有数据满足 $1\le x,y,z\le 10^6$。

本题原始满分为 $15\text{pts}$。

---

只需算出其中任意两个数的最大公因数，再用这个最大公因数去和另一个数求最大公因数即可。

#include<iostream>using namespace std;int gcd(int x, int y)
{if(y == 0) return x;return gcd(y, x % y);
}int main()
{int x, y, z;cin >> x >> y >> z;cout << gcd(gcd(x, y), z) << endl;return 0;
}

---

3. 有大整数的最大公因数 ⭐⭐

【题目链接】

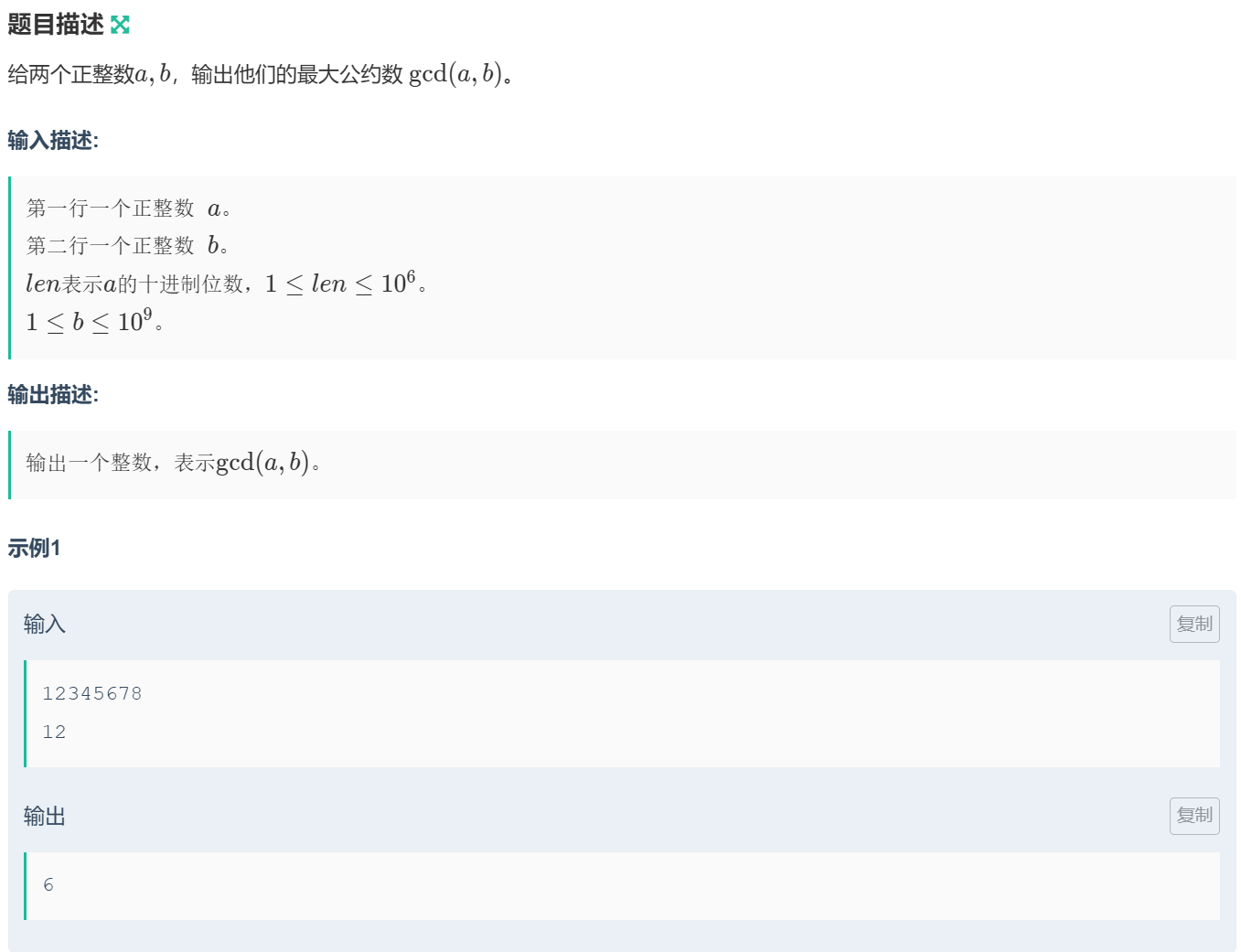
小红的 gcd

---

(1) 补充：秦九韶算法

对于一个 $n$ 次多项式：
$$P(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\cdots +a_{1}x+a_0$$
可以改写为：
$$P(x)=(\cdots ((a_{n}x+a_{n-1})x+a_{n-2})x+\cdots +a_1)x+a_0$$
比如
$$3\times 2^4+5\times 2^3+6\times 2^2+4\times 2+1$$
根据秦九韶算法，可以写成
$$(((3\times 2+5)\times 2+6)\times 2+4)\times 2+1$$
时间复杂度为 $O(n)$。

---

(2) 解题思路

那么对于这道题来说，由于 $a$ 可能非常大，我们只能用 string 字符串来存储它。而我们要计算 $(a,b)$，只需计算 $(b,a\mathrm{mod}b)$ 即可，问题就转换成了计算 $a\mathrm{mod}b$。对于一个数字 $a$，比如它是 $1234$，那么我们可以把它写成
$$1\times 10^3+2\times 10^2+3\times 10+4$$
利用秦九韶算法，可以写成
$$((1\times 10+2)\times 10+3)\times 10+4$$
这样我们就可以只对数字的每一位进行操作，这符合字符串的操作模式。我们只需从前往后取出每一位的数字，将它乘 $10$ 再加上后一位，这样一边计算一边取模，最终得到的结果就是 $a\mathrm{mod}b$ 的结果。

#include<iostream>using namespace std;int gcd(int x, int y)
{if(y == 0) return x;return gcd(y, x % y);
}int main()
{string sa;int b;cin >> sa >> b;// 防止 a * 10 溢出long long a = sa[0] - '0';for(int i = 1; i < sa.size(); i++){a = (a * 10 + sa[i] - '0') % b;}cout << gcd(b, a) << endl;return 0;
}