排序算法:详解快速排序

快速排序介绍
快速排序是一种高效的分治排序算法,由Tony Hoare在1960年提出。它的核心思想是"分而治之",通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,然后分别对这两部分记录继续进行排序,以达到整个序列有序。
快速排序实现
一、工作原理
原始数组: [10, 7, 8, 9, 1, 5]
步骤1: 选择基准元素(这里选择最后一个元素5)
步骤2: 分区操作,将小于5的放在左边,大于5的放在右边[1, 5, 8, 9, 10, 7] // 5已经在正确位置
步骤3: 递归排序左半部分[1]和右半部分[8, 9, 10, 7]左半部分[1]已经有序右半部分选择基准7 → [7, 9, 10, 8] → 继续递归...
二、分区过程详解
分区是快速排序的核心操作,以最后一个元素为基准:
数组: [10, 80, 30, 90, 40, 50, 70]
基准: 70分区过程:
i = -1, j = 0: 10 < 70 → 交换arr[++i]和arr[j] → [10, 80, 30, 90, 40, 50, 70]
i = 0, j = 1: 80 > 70 → 不交换
i = 0, j = 2: 30 < 70 → 交换 → [10, 30, 80, 90, 40, 50, 70]
i = 1, j = 3: 90 > 70 → 不交换
i = 1, j = 4: 40 < 70 → 交换 → [10, 30, 40, 90, 80, 50, 70]
i = 2, j = 5: 50 < 70 → 交换 → [10, 30, 40, 50, 80, 90, 70]
最后交换基准: 交换arr[i+1]和arr[high] → [10, 30, 40, 50, 70, 90, 80]
基准70已经在正确位置!
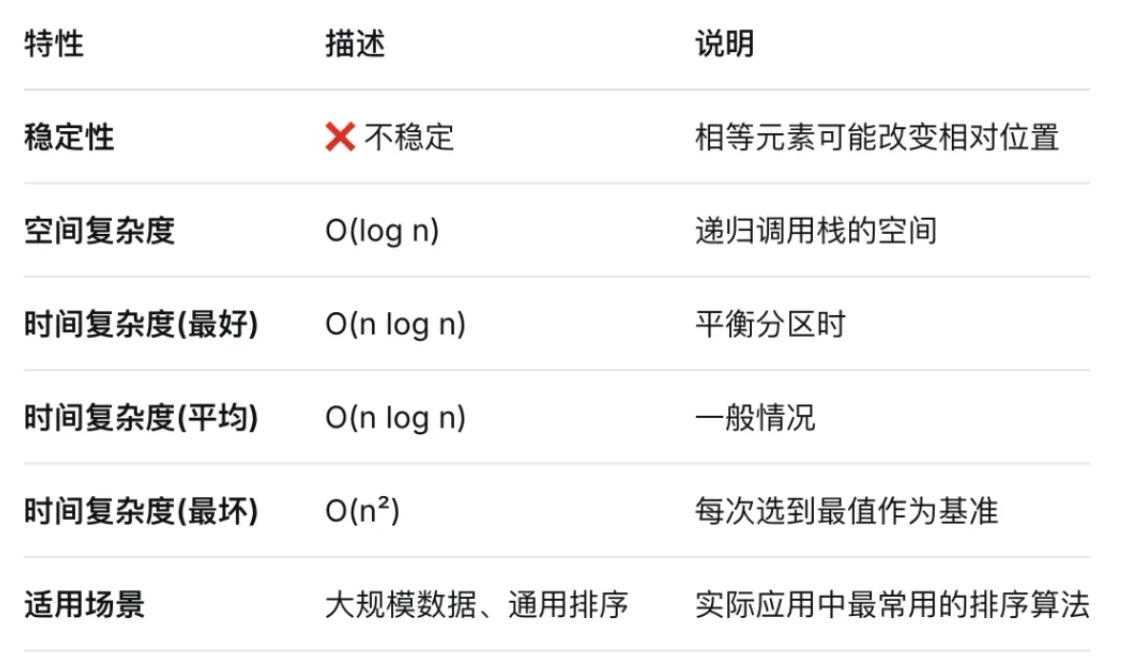
算法特点
代码实现
一、基础版(Lomuto分区方案)
public class QuickSortBasic {/*** 快速排序主方法*/public static void quickSort(int[] arr) {if (arr == null || arr.length <= 1) {return;}quickSort(arr, 0, arr.length - 1);}/*** 递归快速排序* @param arr 待排序数组* @param low 起始索引* @param high 结束索引*/private static void quickSort(int[] arr, int low, int high) {if (low < high) {// 分区操作,获取基准元素的正确位置int pivotIndex = partition(arr, low, high);System.out.println("基准元素 " + arr[pivotIndex] + " 已就位,数组状态: " + arrayToString(arr, low, high));// 递归排序左半部分quickSort(arr, low, pivotIndex - 1);// 递归排序右半部分quickSort(arr, pivotIndex + 1, high);}}/*** Lomuto分区方案* @return 基准元素的最终位置*/private static int partition(int[] arr, int low, int high) {// 选择最后一个元素作为基准int pivot = arr[high];System.out.println("分区: [" + low + "-" + high + "], 基准: " + pivot);// i指向小于基准的区域的边界int i = low - 1;for (int j = low; j < high; j++) {// 如果当前元素小于或等于基准if (arr[j] <= pivot) {i++;swap(arr, i, j);if (i != j) {System.out.println(" 交换 " + arr[j] + " 和 " + arr[i] + " → " + arrayToString(arr, low, high));}}}// 将基准元素放到正确位置swap(arr, i + 1, high);System.out.println(" 基准就位: " + arrayToString(arr, low, high));return i + 1;}/*** 交换数组中的两个元素*/private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}/*** 辅助方法:打印数组指定范围*/private static String arrayToString(int[] arr, int low, int high) {StringBuilder sb = new StringBuilder("[");for (int i = low; i <= high; i++) {sb.append(arr[i]);if (i < high) sb.append(", ");}sb.append("]");return sb.toString();}public static void main(String[] args) {int[] arr = {10, 7, 8, 9, 1, 5};System.out.println("原始数组: " + java.util.Arrays.toString(arr));System.out.println("开始快速排序:");quickSort(arr);System.out.println("排序结果: " + java.util.Arrays.toString(arr));}
}
二、优化版(Hoare分区方案+三数取中)
public class OptimizedQuickSort {/*** 优化版快速排序* 优化点1: 使用Hoare分区方案,减少交换次数* 优化点2: 三数取中法选择基准,避免最坏情况* 优化点3: 小数组使用插入排序*/public static void quickSortOptimized(int[] arr) {if (arr == null || arr.length <= 1) return;quickSortOptimized(arr, 0, arr.length - 1);}private static void quickSortOptimized(int[] arr, int low, int high) {// 小数组使用插入排序if (high - low + 1 <= 10) {insertionSort(arr, low, high);return;}if (low < high) {// 选择基准并分区int pivotIndex = hoarePartition(arr, low, high);// 递归排序quickSortOptimized(arr, low, pivotIndex);quickSortOptimized(arr, pivotIndex + 1, high);}}/*** Hoare分区方案 - 更高效的分区方法*/private static int hoarePartition(int[] arr, int low, int high) {// 三数取中法选择基准int pivot = medianOfThree(arr, low, high);int i = low - 1;int j = high + 1;while (true) {// 从左向右找到第一个大于等于基准的元素do {i++;} while (arr[i] < pivot);// 从右向左找到第一个小于等于基准的元素do {j--;} while (arr[j] > pivot);// 如果指针相遇,返回分区位置if (i >= j) {return j;}// 交换元素swap(arr, i, j);}}/*** 三数取中法:选择左、中、右三个数的中值作为基准*/private static int medianOfThree(int[] arr, int low, int high) {int mid = low + (high - low) / 2;// 对三个数进行排序if (arr[low] > arr[mid]) swap(arr, low, mid);if (arr[low] > arr[high]) swap(arr, low, high);if (arr[mid] > arr[high]) swap(arr, mid, high);// 将中值放在high-1位置,返回中值作为基准swap(arr, mid, high);return arr[high];}/*** 插入排序,用于小数组*/private static void insertionSort(int[] arr, int low, int high) {for (int i = low + 1; i <= high; i++) {int key = arr[i];int j = i - 1;while (j >= low && arr[j] > key) {arr[j + 1] = arr[j];j--;}arr[j + 1] = key;}}private static void swap(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;}public static void main(String[] args) {int[] arr = {64, 34, 25, 12, 22, 11, 90, 5, 77, 30, 15, 42};System.out.println("原始数组: " + java.util.Arrays.toString(arr));quickSortOptimized(arr);System.out.println("排序结果: " + java.util.Arrays.toString(arr));}
}
使用建议
- 推荐使用:大规模数据排序、通用排序需求
- 避免使用:需要稳定排序的场景、对最坏性能要求严格的场景
- 优化重点:合理的基准选择、处理小数组、避免最坏情况
快速排序以其优异的平均性能和缓存友好性,成为实际应用中最常用的排序算法之一!
架构设计之道在于在不同的场景采用合适的架构设计,架构设计没有完美,只有合适。
在代码的路上,我们一起砥砺前行。用代码改变世界!
- 工作 3 年还在写 CRUD,无法突破技术瓶颈?
- 想转技术管理但不会带团队?
- 想跳槽没有面试的机会?
- 不懂如何面试,迟迟拿不到 offer?
- 面试屡屡碰壁,失败原因无人指导?
- 在竞争激烈的大环境下,只有不断提升核心竞争力才能立于不败之地。
欢迎从事编程开发、技术招聘 HR 进群,欢迎大家分享自己公司的内推信息,相互帮助,一起进步!
—— 斩获心仪Offer,破解面试密码 ——


