当前位置：首页 > news >正文

机器学习-强化学习

news 2025/10/18 16:20:14

引入：

假设目前有一个机器人位于下图位置4中，同时位置1和位置6是希望机器人到达进行探索的位置，根据重要程度分别设置奖励Reward值为100和60，那么此时的机器人应该如何进行运动？同类的，实际中还有很多类似的问题，比如无人机的操控、自动象棋系统等等。强化学习算法的思想是：比起直接给定在每一个位置时的最有操作/输出确定的y值，此处引入奖励来提供更多的灵活性；不直接给定要怎么做，而是说明要完成什么。

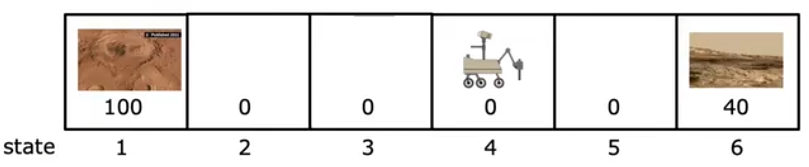
变量定义：

$s$ —— 当前位置

$a$ —— 在当前位置采取的操作

$s^{'}$ —— 操作后下一步所处的位置

$a^{'}$ —— 在下一位置采取的操作

$R(s)$ —— 位置s对应的奖励值

回报与状态-动作值函数：

关于上图中的问题，我们可以有很多种不同的路径选择，分别会得到不同的奖励，也会有不同的消耗。显然的，如果能够更迅速地得到奖励，相比起需要耗费很多才能够得到奖励，前者可能更具有吸引力。因此此处引入折现因子，由此定义得到回报：

$Return = R(s_{0})+\gamma R(s_{1})+\gamma ^{2}R(s_{2})...$

上述表达式可以计算出按照 $s_{0}\rightarrow s_{1}\rightarrow s_{2}...\rightarrow terminal\ state$ 路径下的得到的回报。假设不论处在什么状态，都一直向左/右行动，直到达到终止状态，那么每个状态对应的回报如下图所示。

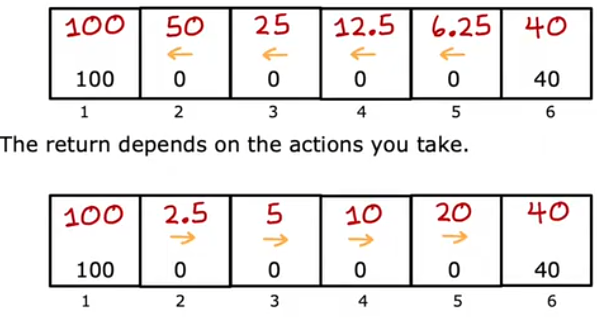
如果存在负奖励，那么为了得到更多的回报，此时算法会尽可能地将负奖励后推，以达到更多次的折现。

综合上述，最终希望的策略应该是能够获得最大回报的策略，也称为 $\pi$ 策略： $s\xrightarrow[]{\pi }a$ ，即在此策略下，输入当前位置即可输出得到对应的最优操作。

状态-动作值函数的定义为： $Q(s,a)$ 表示处于状态s，采取操作a，且之后都按照最优方式行动所能获得的所有回报。还是以图一为例，下图上部展示出了在不同位置时，能获得的最大回报以及对应的行动，下部则展示了采取不同行动方式对应的最大回报，也就是每个状态和动作下对应的状态-动作值函数值。

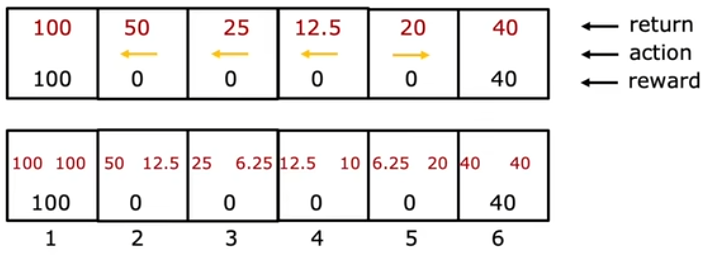
bellman方程的表达式如下：

$Q(s,a)=R(s)+\gamma \underset{a^{'}}{max}Q(s^{'},a^{'})$

该方程将状态-动作值函数用数学形式表达出来，并且对比之前回报的表达式可以发现：

$R(s_{0})+\gamma R(s_{1})+\gamma ^{2}R(s_{2})...= R(s_{0})+\gamma (R(s_{1})+\gamma R(s_{2})...)$

因此，bellman方程实际上是把回报分为了两个部分，一部分是当前状态的立即获得的奖励，一部分则是动作后存在折现的、且采取最优动作的回报。

不过，上述的分析都是建立在没有任何意外的情况下的。实际操作过程中，有可能采取了某动作，但执行失败的情况，因此我们更需要的是回报的平均值，对应bellman方程为：

$Q(s,a)=R(s)+\gamma E(\underset{a^{'}}{max}Q(s^{'},a^{'}))$

深度Q网络(DQN)：

在实际应用中，对应的状态往往不是上述的几个离散点，而是连续的，对不同的任务，状态信息的描述也不一样，如果是对于AGV小车，其状态信息可以表示为： $[x,y,\theta ,\dot{x},\dot{y},\dot{\theta }]$ 。而有关动作的信息则可以转换为独热编码。

结合前述可知，一个好的策略是尽量在当前状态下采用使得状态-动作值函数最大的动作，以获得最多的回报。为了得到一个好的策略，我们需要学习得到最优Q函数，那么关于训练学习所需要的数据，应该如何获取呢？
在学习初期，此时还没有一个较好的策略来指导动作，因此我们可以通过随机动作来获取大量的 $(s,a,R(s),s^{'})$ 数据，并建立如下图所示的网络：即将输入定义为： $x=(s,a)$ ，将输出定义为： $y=Q(s,a)$ 。

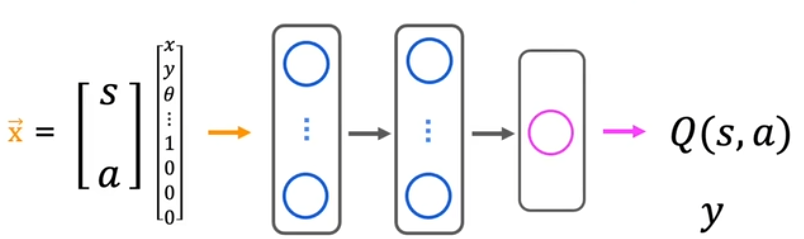
结合Q函数的表达式可知，此时的输入根据样本数据是已知的，但是Q函数值却无法计算，因为此时我们还没的学习得到Q函数。因此，在训练的初期，需要随机神经网络参数以获得初始的Q函数，此时的损失可以定义为：

$L=Q(s,a)-[R(s)+\gamma \underset{a^{'}}{max}Q(s^{'},a^{'})]$

观察上式可知： $Q(s,a)$ 与 $Q(s^{'},a^{'})$ 是通过学习得到的Q函数的预测值，而 $R(s)$ 则是关于即时奖励的真实值。通过不断地学习，调整参数，就可以使模型的预测更加符合bellman方程所描述的关系。

整体流程可总结为：

随机初始化神经网络参数；
随即不同动作得到大量（一般是10000个） $(s,a,R(s),s^{'})$ 数据；
创建训练集： $x=(s,a)$ ， $y=Q(s,a)$ ；
训练网络，不断优化Q函数。

在训练过程中，有以下需要注意的部分：

Soft Update：

在前面的训练过程中，一旦模型参数发生更新，对应的Q值均会发生更新，但这种做法其实是不利于模型收敛的，因为这意味着在训练中目标随时都在发生更新变化，且这个变化可能很大。因此采用软更新是一种较好的解决方案，以梯度下降为例：

$\left\{\begin{matrix} w_{new}=w-\alpha \frac{\partial J}{\partial w}\rightarrow w=0.01w_{new}+0.99w\\ b_{new}=b-\alpha \frac{\partial J}{\partial b}\rightarrow b=0.01b_{new}+0.99b \end{matrix}\right.$

在此情况下，参数的更新是渐进式的，更有利于算法的收敛。

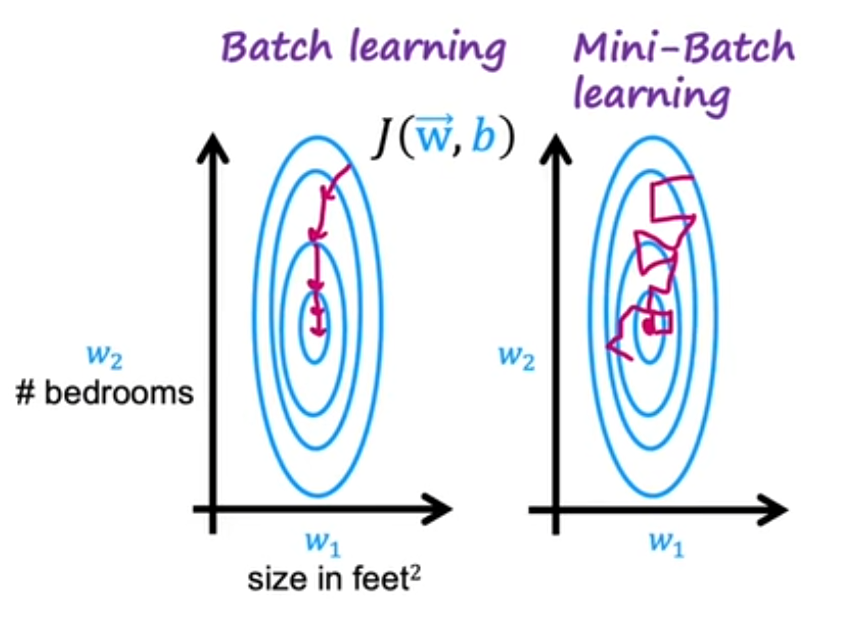
小批量训练：

当存在大量的训练样本时，一次性的统一将所有样本投入训练会导致训练过程十分缓慢。因此在这种情况下可以采用小批量训练，即每次训练时只投入一部分的样本。

有时候这些样本恰好代表了整个数据集的分布，梯度方向接近最优；当然也有可能某一次“比较难”或者包含一些异常样本，其梯度方向会偏离全局最优方向，甚至指向一个暂时“上升”的方向，但是长远来看，小批量训练是可以找到全局最小值的。

改进网络结构：

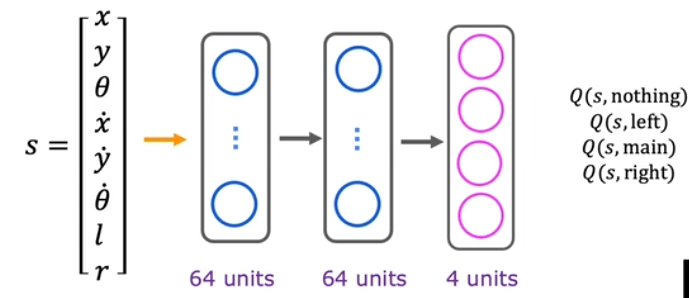
根据之前的网络结构可知，每次都需要对不同的动作重新推理来得到对应的Q值，这样实际上是非常低效的，尤其是在样本量较多的时候。因此可以考虑改进网络结构，将输出层改为多个单元，分别对应不同动作对应的Q值，以便于后续更新。

$\varepsilon$ -贪心策略：

假设目前仍然还在学习的过程中，当位于某一个状态时，应该如何采取动作？一般来说，此时会采取使得Q值最大的动作，这也就对应着贪心策略。但需要注意的是，初始的神经网络参数时随机得到的，因此有可能某一种动作对应的Q值一直很低，如果仍然采用贪心策略，将永远不会去探索此动作会不会是一种好操作的可能性。所以，在学习的初期，我们应该鼓励进行更多的探索，而在中后期则可以适当的降低探索的比例。 $\varepsilon$ 就代表了探索的比重，若 $\varepsilon =0.05$ ，则在5%的情况下，我们会随机动作，而在剩下95%的情况下，则会选择使得Q值最大化的动作。