深度学习2-损失函数-数值微分-随机梯度下降法（SGD）-反向传播算法

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

前言

神经网络的主要特点，就是可以从数据中进行“学习”。这个学习的过程，就是让训练数据自动决定最优的权重参数。
神经网络（深度学习）也是机器学习的一种；跟传统机器学习方法相比，神经网络不需要人工设置 特征量（如 SIFT、HOG等）不要特征工程特征降维，这样就可以用同样的流程直接处理所有问题了。

1. 损失函数

神经网络中，需要以某个指标为线索来寻找最优权重参数；这个指标就是 损失函数

3.1.1常见损失函数
1）均方误差（MSE）—》回归问题

2）交叉熵误差—》分类问题

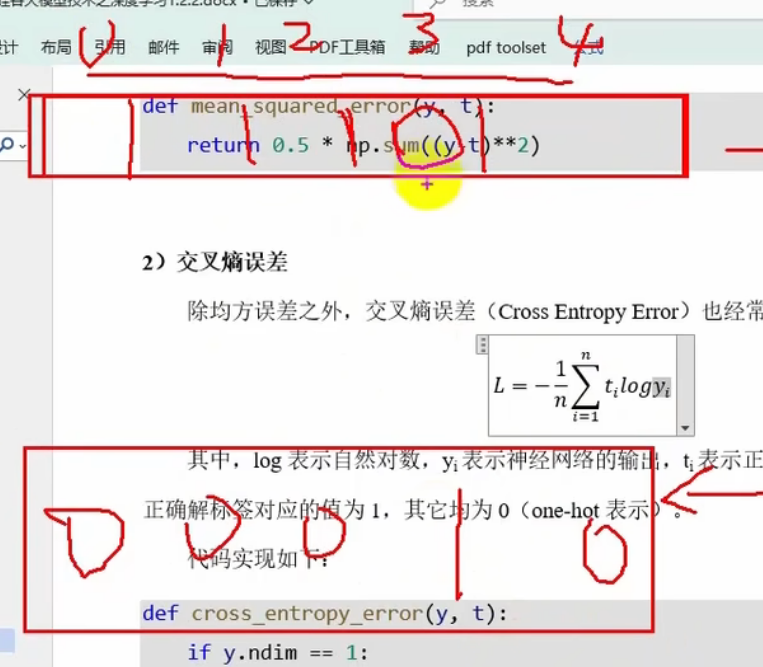
#损失函数
def mean_squared_error(y, t):return 0.5 * np.sum((y - t)**2)

y和t就是一个向量，对应位置相减

y指的是每个类的概率

t是正确类概率为1，其他为0

其实就是计算正确类的预测概率的log值的和

def cross_entropy_error(y, t):#统一维度，将预测值转为二维,y就是概率值if y.ndim == 1:t = t.reshape(1, t.size)y = y.reshape(1, y.size)# 这里的y，t就是二维了if t.size == y.size:t = t.argmax(axis=1)n = y.shape[0]# y[np.arange(n),t]表示取第一行某类的概率值，np.arange(n),t就是取概率值的坐标# 1e-10的原因是防止log取0，1e-10是一个微小值return -np.sum(np.log(y[np.arange(n),t]+1e-10)) / n

1.1 分类任务损失函数

1）二分类任务损失函数

二分类任务常用二元交叉熵损失函数（Binary Cross-Entropy Loss）。

2）多分类任务损失函数
多分类任务常用多类交叉熵损失函数（Categorical Cross-Entropy Loss）。它是对每个类别的预测概率与真实标签之间差异的加权平均。

1.2 回归任务损失函数

回归问题就是数值输出
回归问题本质上是一种预测连续数值输出的机器学习任务，核心是找到输入变量和输出变量之间的映射关系。

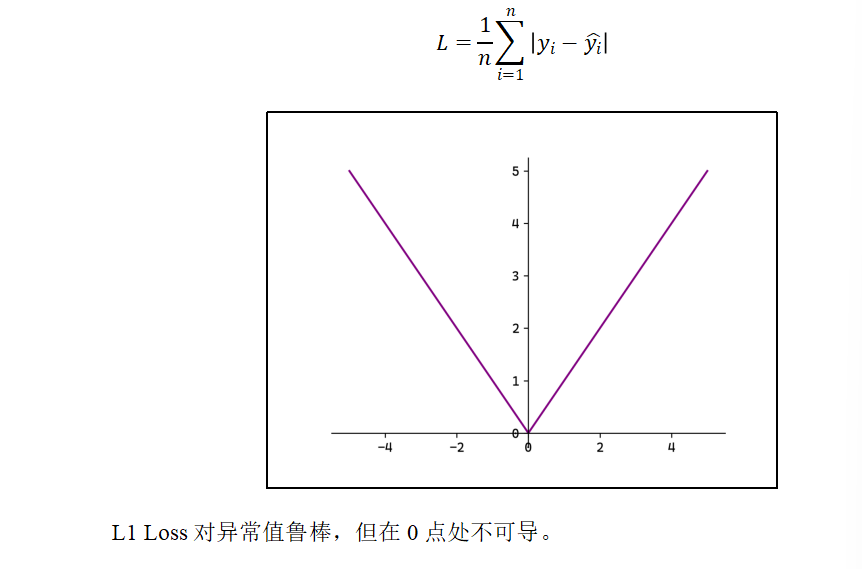
1）MAE
平均绝对误差（Mean Absolute Erro，MAE），也称L1 Loss：

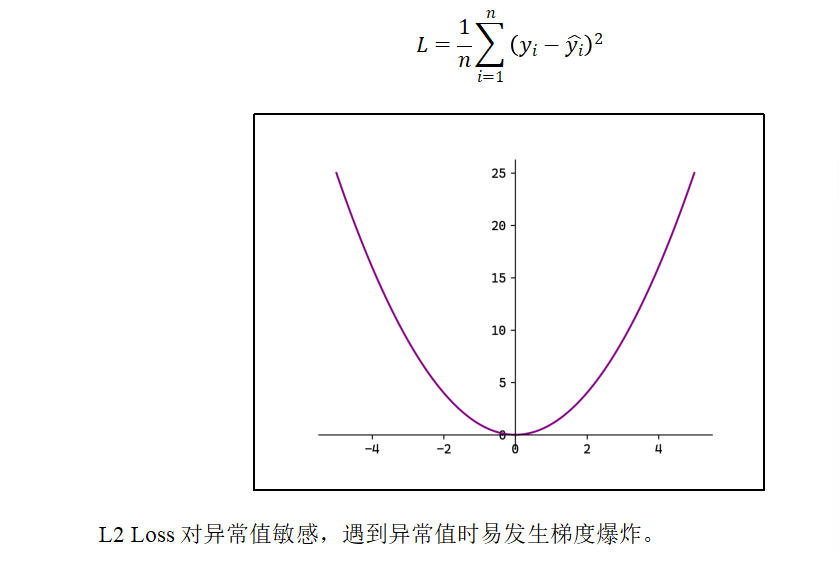
2）MSE
均方误差（Mean Squared Error ，MSE），也称L2 Loss：

2. 数值微分

损失函数的值越小，代表我们选取的参数越适合；想要求得损失函数的最小值，最基本的想法就是对函数求导，解出导数值为0的点，并判断它是否为极小值/最小值。
然而，实际的函数直接求导，不容易得到解析解。这时可以用数值微分的方式来求某点处的导数，这在工程上应用非常广泛。

2.1 导数和数值微分

给出一个x，只需要进行前向传播，就可以知道y了，然后就可以计算变换率了，然后就可以计算导数值了

这样就不需要知道f函数

def numerical_gradient(f, x):h = 1e-4    #0.0001return (f(x+h)-f(x-h)) / (2*h)

同时向x点靠近，就是最好的导数值
取微小值h时不能太小，这会导致计算机浮点数表示的精度不够，出现舍入误差

#数值微分求导
import numpy as np
import matplotlib.pyplot as pltdef numerical_gradient(f, x):h = 1e-4    #0.0001return (f(x+h)-f(x-h)) / (2*h)#原函数
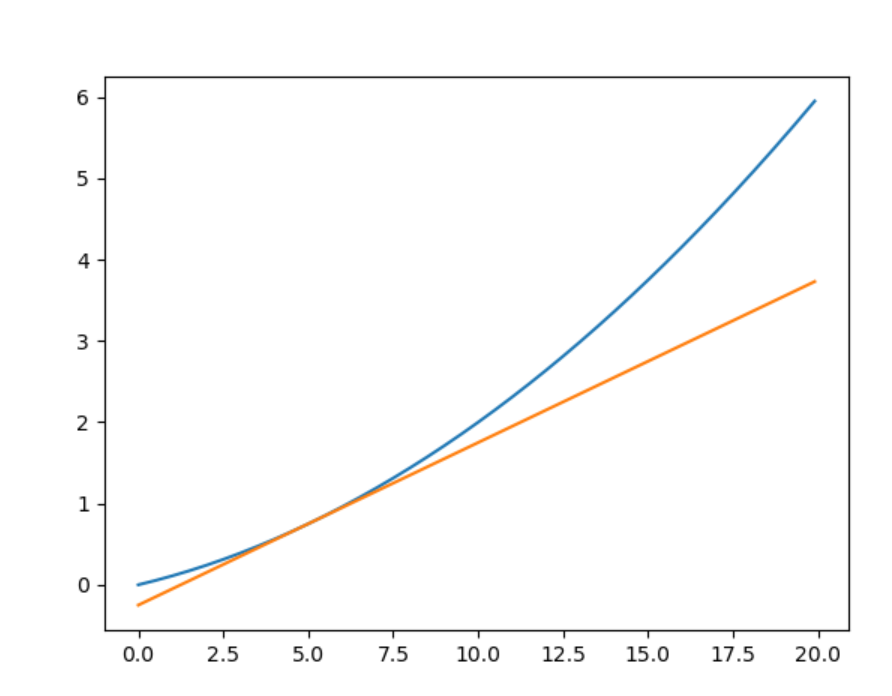
def f(x):return 0.01 * x**2 + 0.1 * x#求出切线方程,y=ax+b
def tangent_line(f,x):y = f(x)a = numerical_gradient(f, x)b = y - a * xreturn lambda x: a * x + b#定义画图范围
x = np.arange(0.0, 20.0, 0.1)
y =f(x)
#计算x=5切线
f_line = tangent_line(f,x=5)
#给出切线上的点
y_line = f_line(x)
plt.plot(x,y)
plt.plot(x,y_line)
plt.show()

2.2 偏导数

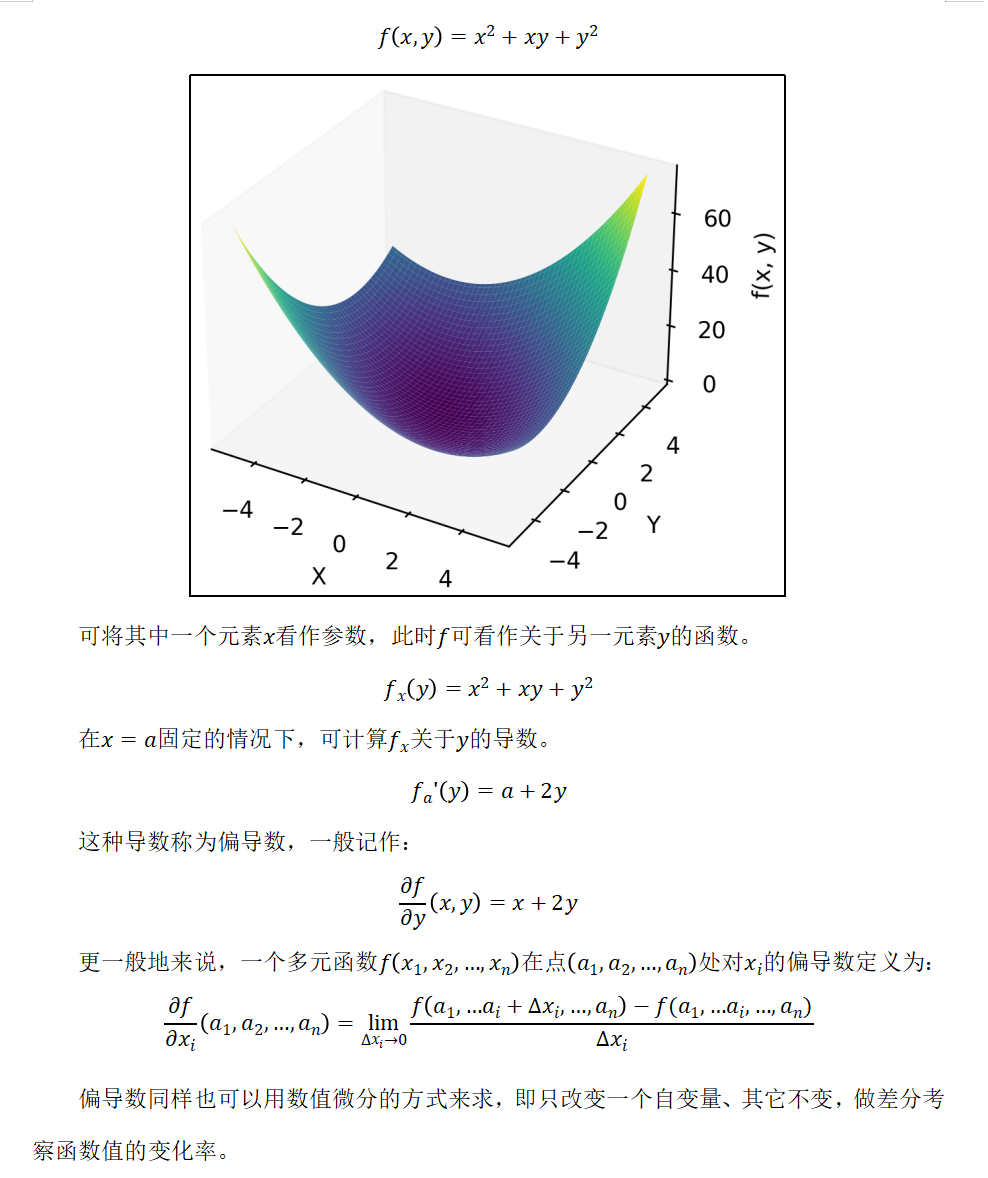
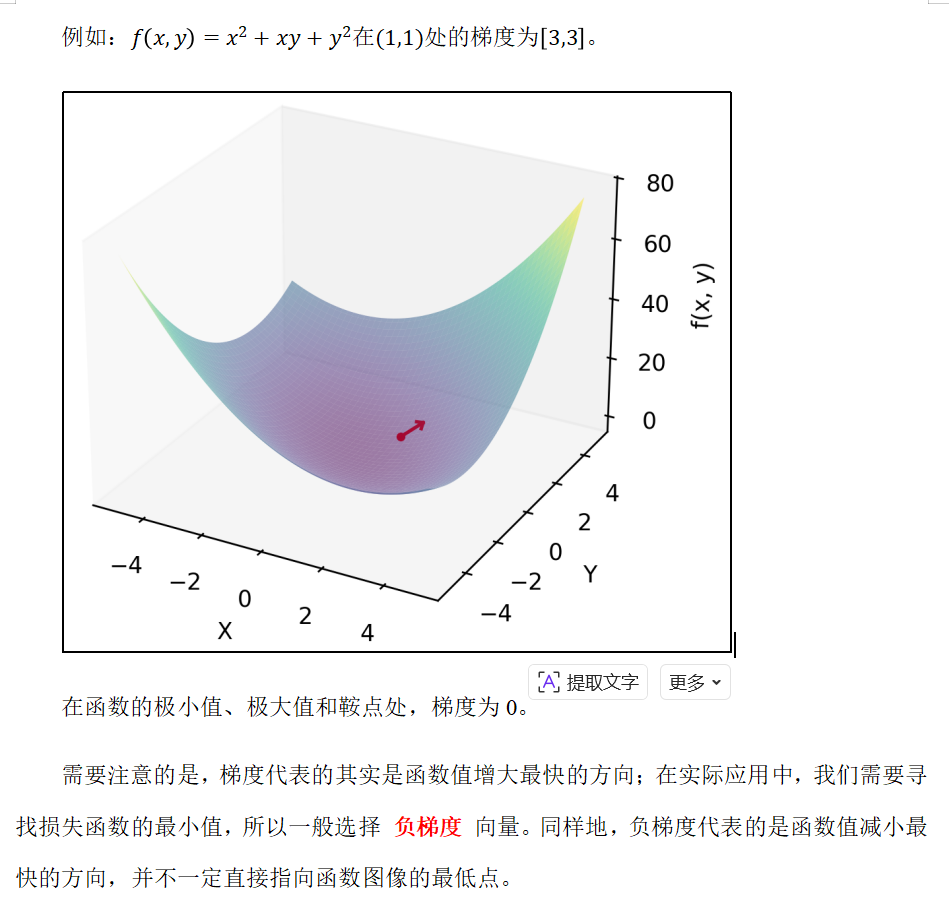
2.3 梯度

#数值微分求梯度,x是一维
def _numerical_gradient(f, x):h = 1e-4grad = np.zeros_like(x)for i in range(x.size):tmp = x[i]x[i] = tmp +hfxh1 = f(x)x[i] = tmp - hfxh2 = f(x)grad[i] = (fxh1-fxh2)/(2*h)#恢复x[i]x[i] = tmpreturn grad#x为二维
def numerical_gradient(f,X):if X.ndim == 1:_numerical_gradient(f,X)else:grad = np.zeros_like(X)for i,x in enumerate(X):grad[i] = _numerical_gradient(f,x)return grad

2.4 神经网络的梯度计算

神经网络中的梯度，指的就是损失函数关于权重参数的梯度。

class simpleNet:def __init__(self):self.W = np.random.randn(2,3)# 前向传播def forward(self, x):a= np.dot(x, self.W)y = softmax(a)return y#计算损失值def loss(self, x, t):z = self.forward(x)y = softmax(z)loss = cross_entropy_error(y, t)return loss

class SimpleNet:def __init__(self):self.W = np.random.randn(2,3)# 前向传播def forward(self, x):a= np.dot(x, self.W)y = softmax(a)return y#计算损失值def loss(self, x, t):z = self.forward(x)y = softmax(z)loss = cross_entropy_error(y, t)return lossif __name__ == '__main__':x = np.array([0.6,0.9])t = np.array([0,0,1])#定义模型net  = SimpleNet()#计算梯度,f为函数f = lambda w : net.loss(x, t)gradw =  numerical_gradient(f,net.W)print(gradw)

3. 随机梯度下降法（SGD）

3.1 梯度下降法

梯度下降法（Gradient Descent）是一种用于最小化目标函数的迭代优化算法。核心是沿着目标函数（如损失函数）的负梯度方向逐步调整参数，从而逼近函数的最小值。梯度方向指示了函数增长最快的方向，因此负梯度方向是函数下降最快的方向。

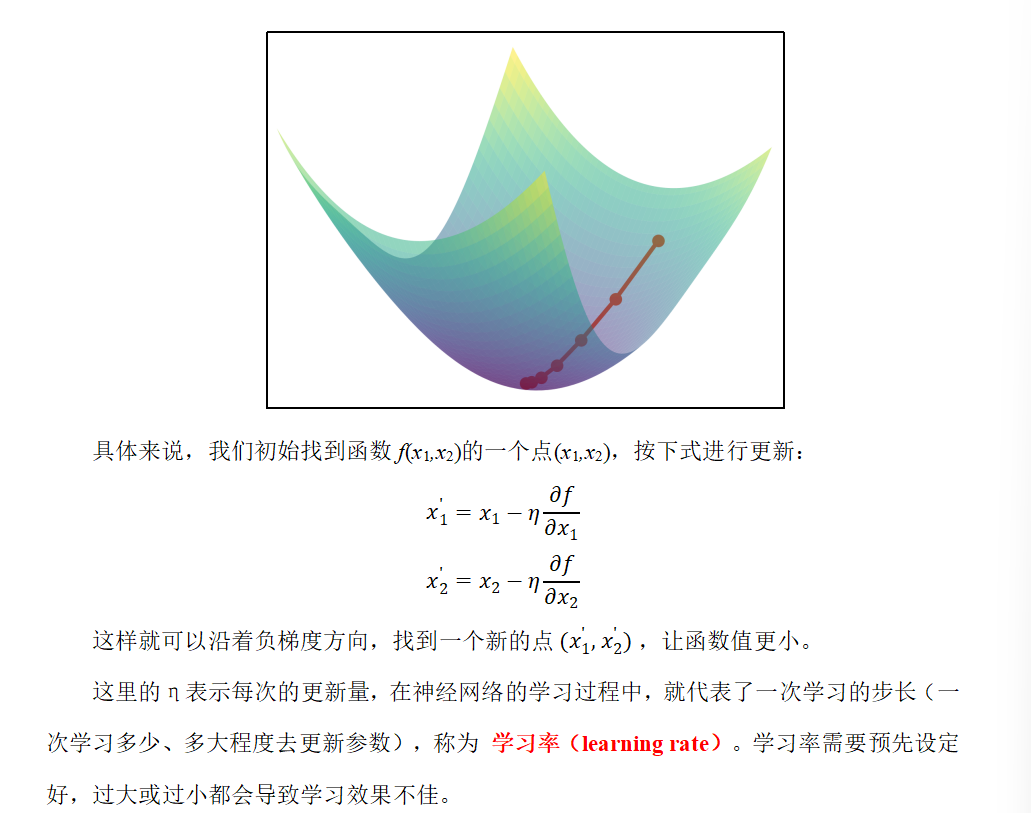
这里的η表示每次的更新量，在神经网络的学习过程中，就代表了一次学习的步长（一次学习多少、多大程度去更新参数），称为 学习率（learning rate）。学习率需要预先设定好，过大或过小都会导致学习效果不佳。

过大就是左右横跳，过小的话，就很慢

def gradient_descent(f, init_x, lr=0.01, step_num=100):x = init_xx_history = []for i in range(step_num):x_history.append( x.copy() )grad = numerical_gradient(f, x)x -= lr * gradreturn x, np.array(x_history)

lr就是学习率，step_num是迭代次数
梯度numerical_gradient就是这个点的斜率
梯度下降法这样就找到了极小值了

# 定义目标函数 f(x1, x2) = x1^2 + x2^2
def f(x):return x[0] ** 2 + x[1] ** 2
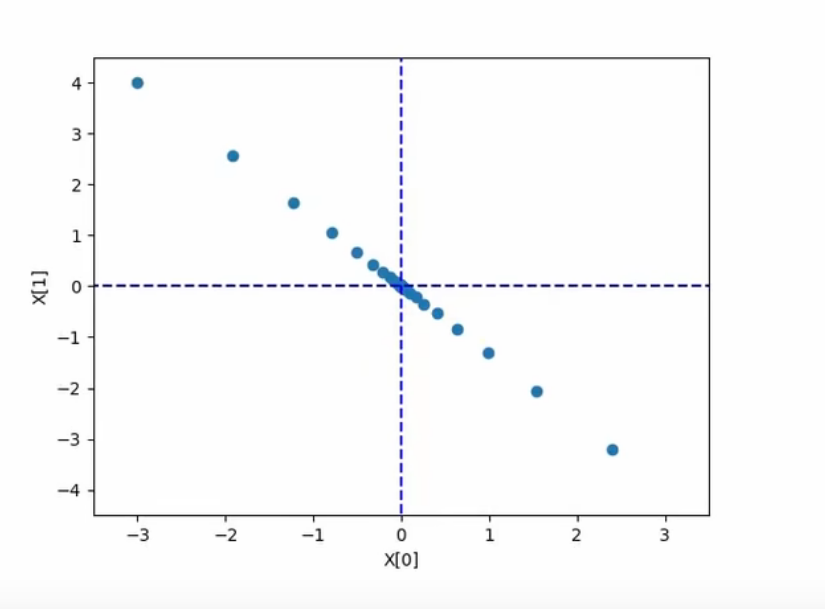
if __name__ == '__main__':# 1. 定义初始值init_x = np.array([-3.0, 4.0])# 2. 定义超参数lr = 0.9num_iter = 200# 3. 使用梯度下降法，计算最小值点x, x_history = gradient_descent(f, init_x, lr, num_iter)print("最小值点为：", x)# 画图plt.plot([-5, 5], [0, 0], '--b')plt.plot([0, 0], [-5, 5], '--b')plt.scatter(x_history[:, 0], x_history[:, 1])plt.xlim([-3.5, 3.5])plt.ylim([-4.5, 4.5])plt.xlabel("X[0]")plt.ylabel("X[1]")plt.show()

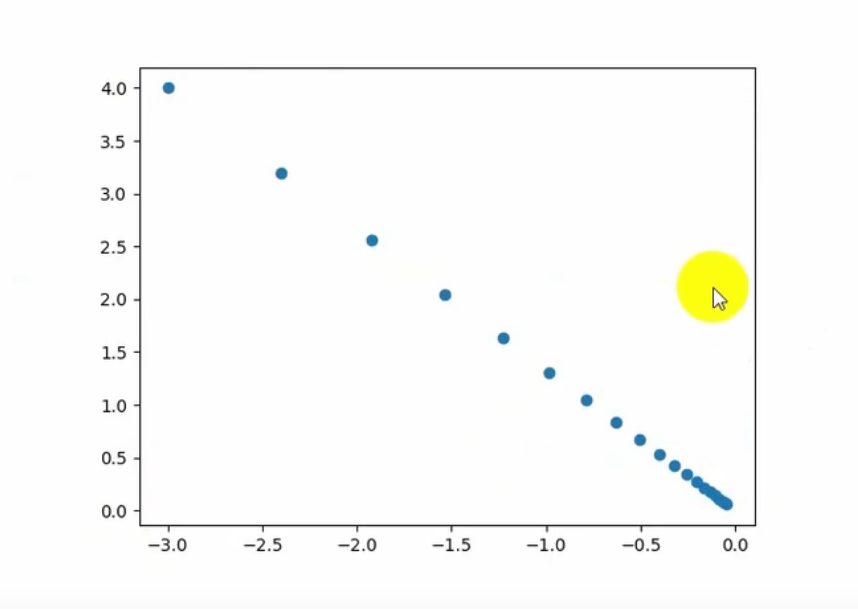
如果学习率太小—》迭代太慢

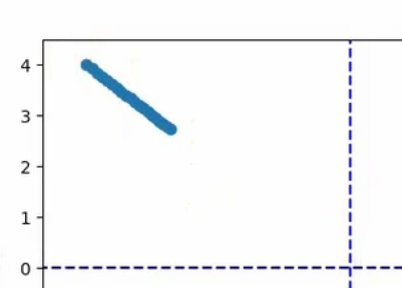
但是可以增加学习率步长，或者增加迭代次数

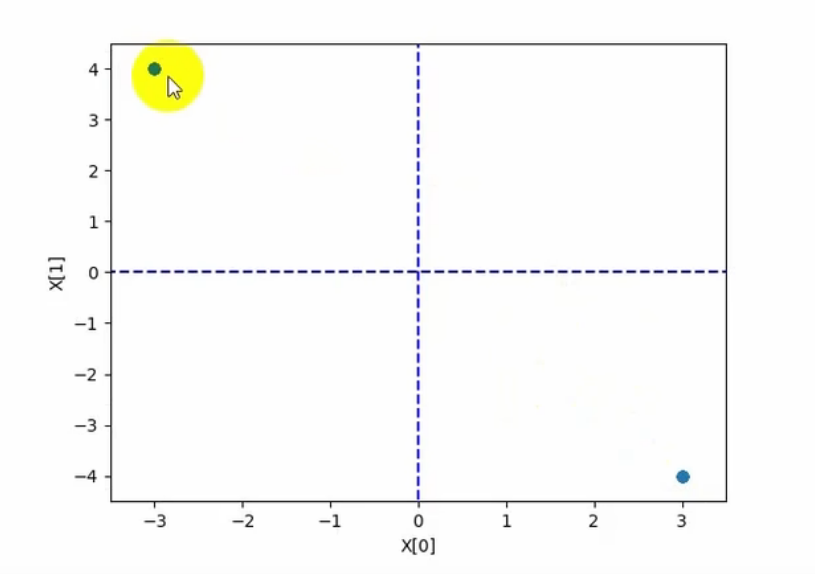
但是学习率太大就是左右横跳

3.2 模型训练相关概念

1）Epoch
1个Epoch表示模型完整遍历一次整个训练数据集的过程。例如，训练10个Epoch表示模型将整个数据集反复学习10次。
模型需要多次遍历数据集（多个Epoch）才能逐步学习数据中的模式，单次遍历数据集（1个Epoch）通常不足以让模型收敛，多次遍历可以逐步优化模型参数。
1个Epoch对应多个Batch Size，多个Iteration

2）Batch Size
Batch Size是每次训练时输入的样本数量。例如，Batch Size=32 表示每次用32个样本计算一次梯度并更新模型参数。
小批量数据计算梯度比单样本（Batch Size=1）更稳定，比全批量（Batch Size=全体数据）更高效。并且较小的Batch Size可能带来更多噪声，有助于模型泛化。

3）Iteration
一次Iteration表示完成一个Batch数据的正向传播（预测）和反向传播（更新参数）的过程。
例如，数据集现有2000个样本，对其训练10个Epoch，选择Batch Size=64：
Batch个数为2000//64+1=31+1=32个（最后一个Batch仅有16个样本）。
每个Epoch中迭代次数Itreation=32次。
总迭代次数为10×32=320次。
总训练样本数为10×2000=20000。

神经网络中采用梯度下降法，都是小梯度的

3.3 SGD

在神经网络的学习过程中，可以使用梯度下降法来更新参数，目标就是减小损失函数的值。
实际操作时，一般会从训练数据中随机选择一个小批量数据（mini-batch），然后用梯度下降法迭代多个轮次（iteration）；这种“对随机选择的数据进行的梯度下降法”，被称作 随机梯度下降法（stochastic gradient descent，SGD）。

1）随机选择批数据（mini-batch）
从训练数据中随机选出一部分数据，学习的目标就是要减少这个mini-batch数据的损失函数值。
2）计算梯度
对当前的各权重参数，计算出梯度的值，负梯度就表示了损失函数减小最多的方向。
3）更新参数
按照前面梯度下降法的公式，对权重参数沿负梯度方向进行微小更新。
4）重复迭代
重复上面的步骤1）2）3），直到完成预定的总迭代次数。

4. 反向传播算法

反向传播（Backward Propagation或Back Propagation，BP算法）指的是计算神经网络参数梯度的方法。简言之，该方法根据微积分中的链式法则，按相反的顺序从输出层到输入层遍历网络。该算法存储了计算某些参数梯度时所需的任何中间变量。

4.1 计算图

算图将计算过程用图表示出来。

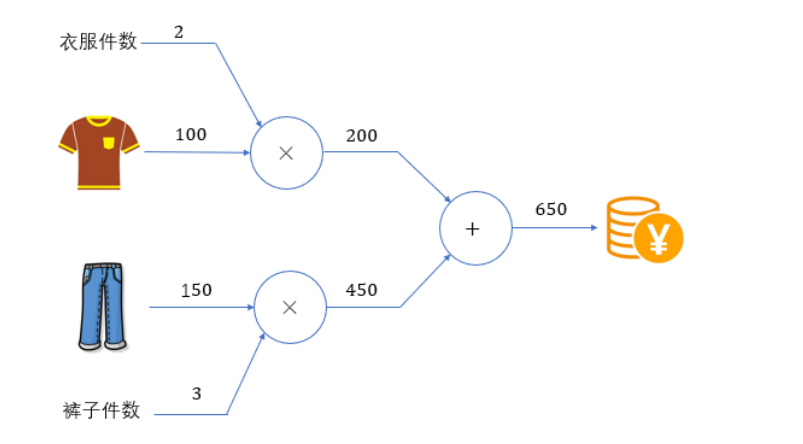
计算图的基本计算原则，就是从输入出发、按照箭头方向，从左到右依次进行计算，最终得到输出结果。这个过程，其实就是 前向传播（forward）。

计算图的特点是可以通过传递“局部计算”获得最终结果。即只需根据与自己相关的信息输出接下来的结果。无论全局的计算有多么复杂，各个节点所要做的就是进行局部计算并传递计算结果，最终得出全局的复杂计算的结果。

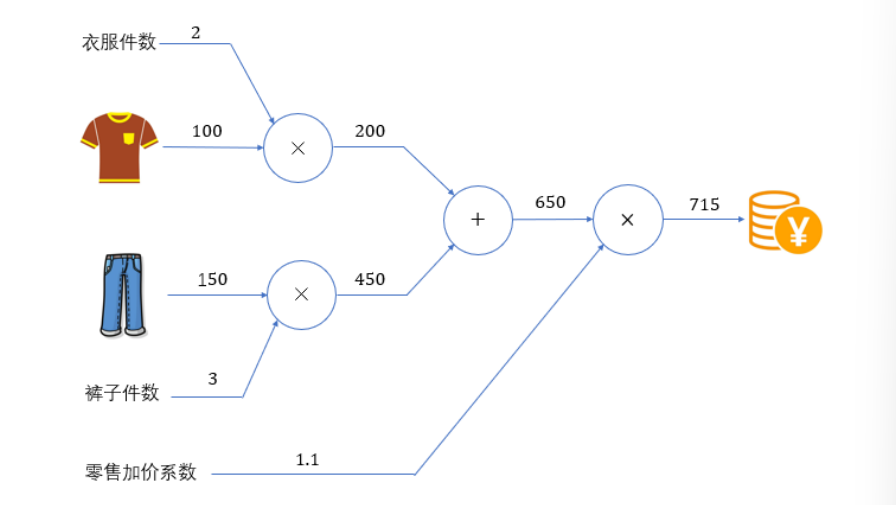
将输入的衣服价格记为x，输出的支付金额记为L，这其实就是要求导数值 。

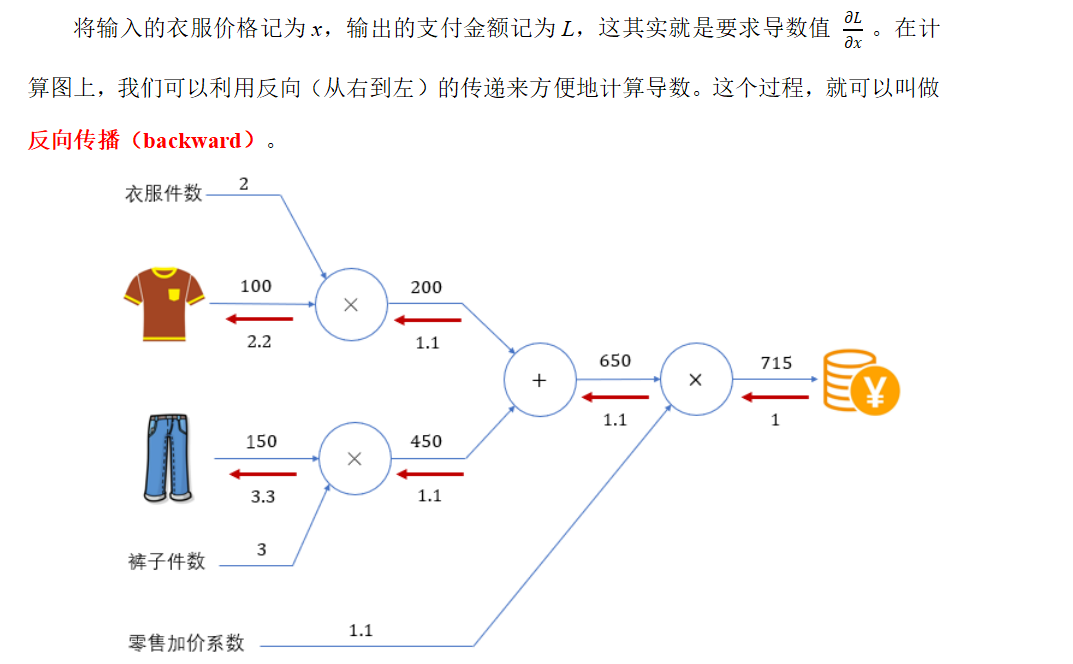
箭头上面的数字就是变化率

4.2 链式法则

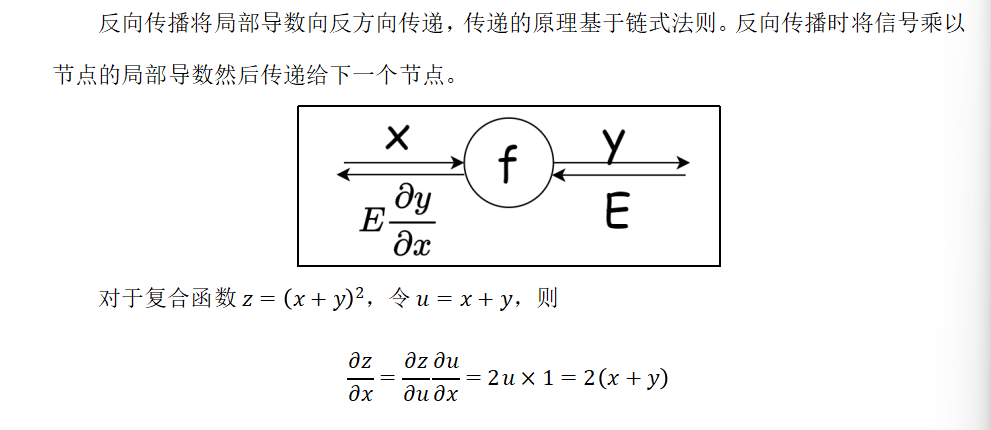
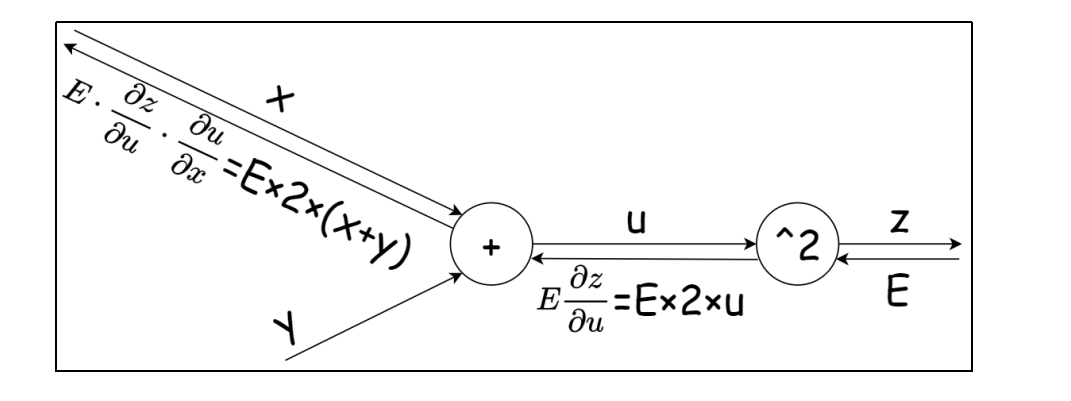
利用计算图的反向传播，可以很容易地计算出输出关于输入的偏导数。

反向的话：这样就只需要计算每一层的导数，然后乘以下一层的导数，就是这一层真正的导数了，很方便

4.3 加法节点的反向传播

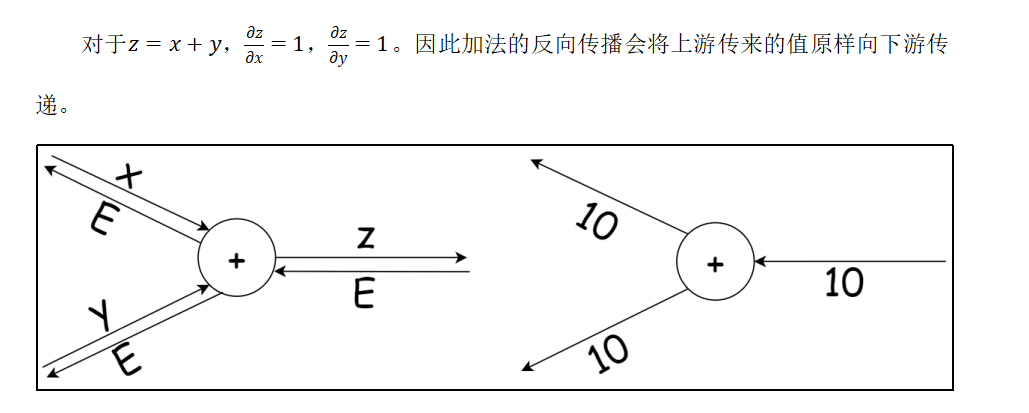
4.4 乘法节点的反向传播

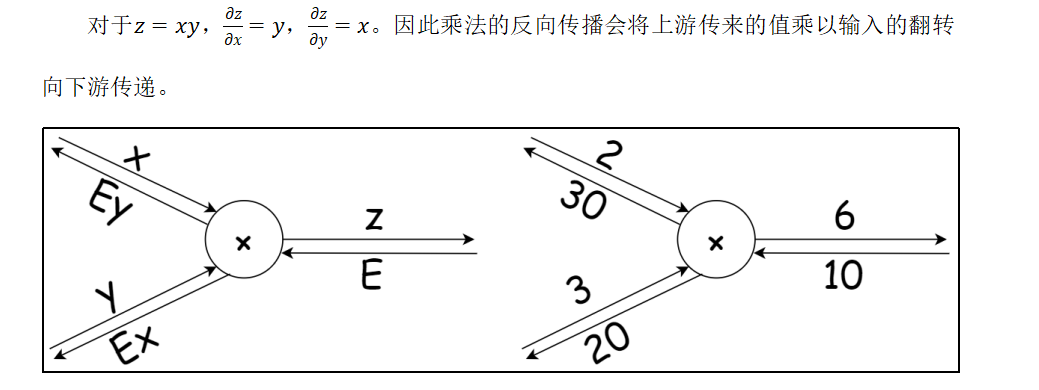
现在将计算图应用到神经网络中。神经网络中一步重要的计算操作就是激活函数，下面就来讨论各种激活函数的反向传播，基于这些我们就可以用代码实现激活层的完整功能了。

4.5 ReLU的反向传播

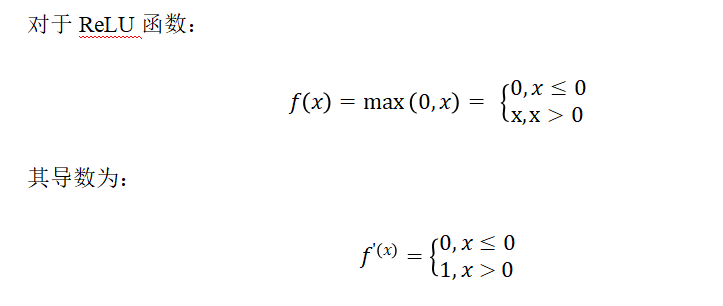
梯度消失就是说导数太小了，梯度爆炸就是导数太大了

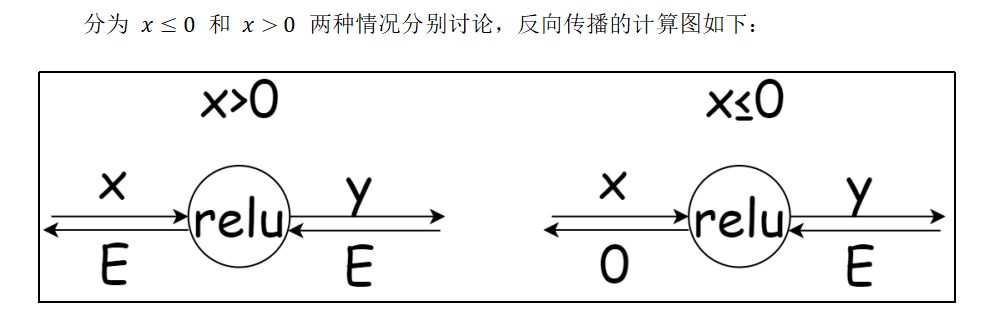
class Relu:def __init__(self):#内部属性，记录哪些x<=0self.mask = Nonedef forward(self, x):self.mask = (x <= 0)out = x.copy()# 将x<=0的值都变为0out[self.mask] = 0return out# dout就是下一步的导数值，求上一步的导数值def backward(self, dout):dout[self.mask] = 0dx = doutreturn dx

4.6 Sigmoid的反向传播

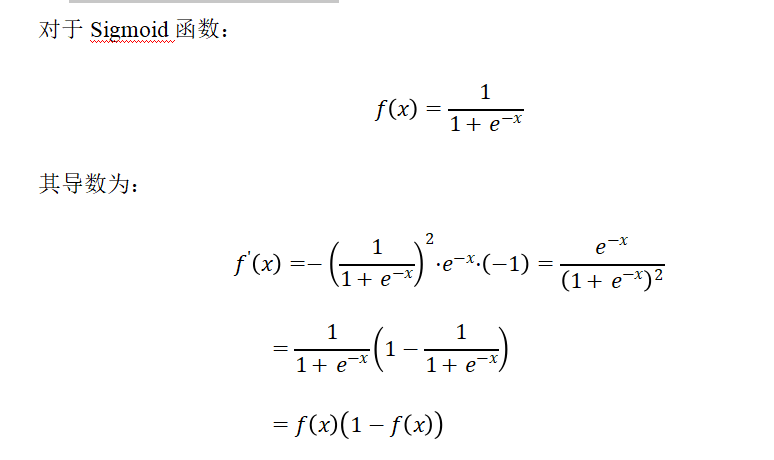
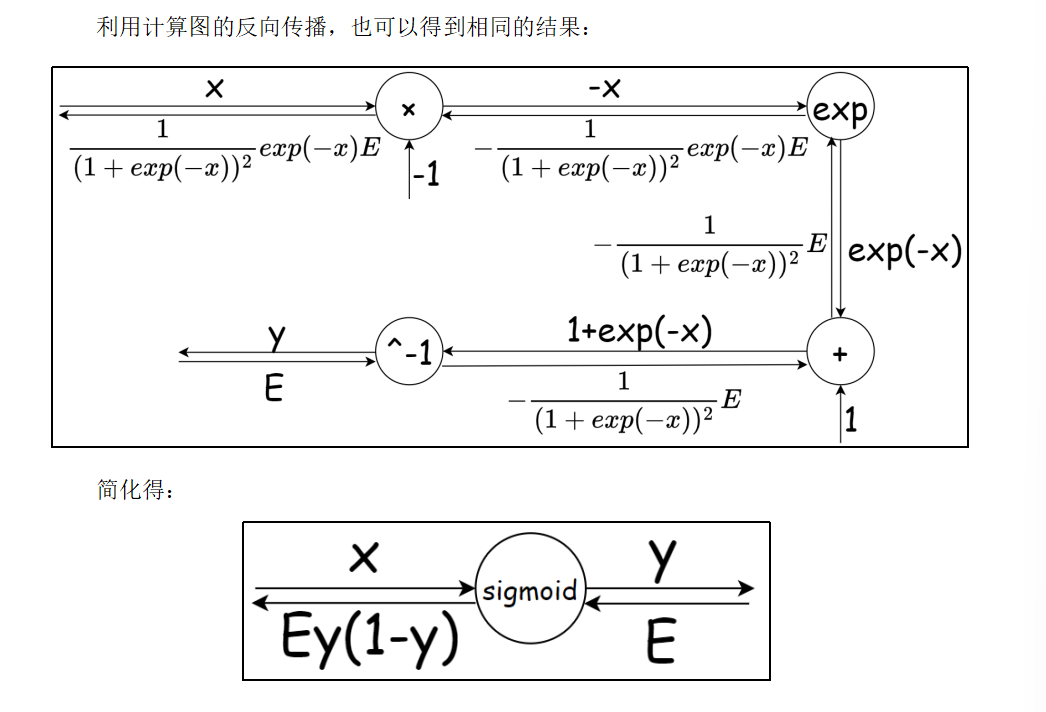
l对x的求导就是y对x的求导l对y的求导E，所以就是Ey(1-y)

class Sigmoid:def __init__(self):self.out = Nonedef forward(self, x):out = sigmoid(x)self.out = outreturn outdef backward(self, dout):dx = dout * (1.0 - self.out) * self.outreturn dx

4.7 Affine的反向传播和实现

在全连接层（Fully Connected Layer，Dense Layer）中，每个输入节点与输出节点相连，通过权重矩阵和偏置进行线性变换，这种操作在几何领域称为仿射变换（Affine transformation，几何中，仿射变换包括一次线性变换和一次平移，分别对应神经网络的加权求和运算与加偏置运算）。
考虑N个数据一起进行正向传播的情况，写成矩阵计算形式：


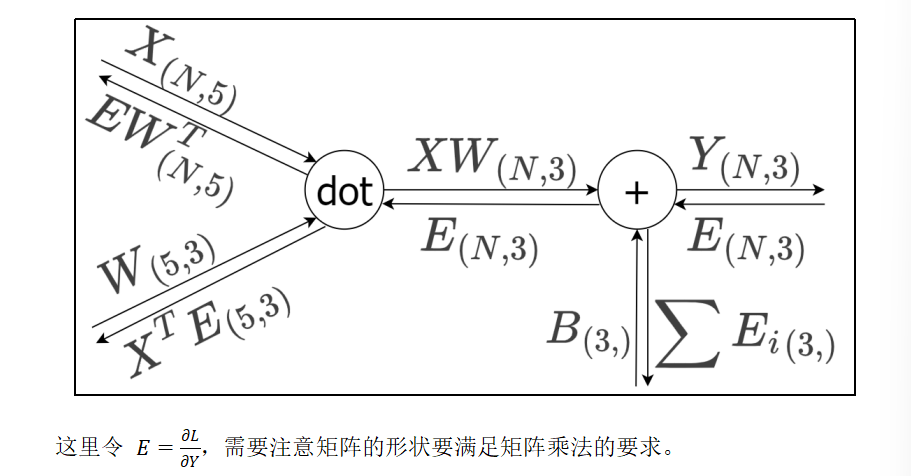
5就是x的特征值，然后也是输入层的个数，输出层个数为3
所以W就是5,3

class Affine:def __init__(self, W, b):self.W = Wself.b = bself.x = Noneself.original_x_shape = None# 权重和偏置参数的导数self.dW = Noneself.db = Nonedef forward(self, x):# 对应张量self.original_x_shape = x.shapex = x.reshape(x.shape[0], -1)self.x = xout = np.dot(self.x, self.W) + self.breturn outdef backward(self, dout):dx = np.dot(dout, self.W.T)self.dW = np.dot(self.x.T, dout)self.db = np.sum(dout, axis=0)dx = dx.reshape(*self.original_x_shape)return dx

4.8 输出层的反向传播和实现

在输出层，我们一般使用Softmax作为激活函数。主要是分类问题

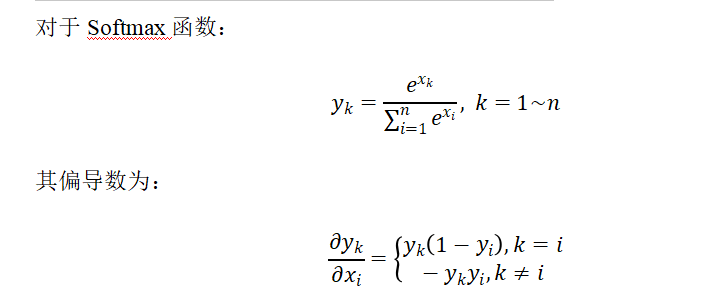
而对于输出层，一般会直接将结果代入损失函数的计算。对于我们之前介绍的分类问题，这里选择交叉熵误差（Cross Entropy Error）作为损失函数，就可以得到一个Softmax-with-Loss层，它包含了Softmax和Cross Entropy Loss两部分。

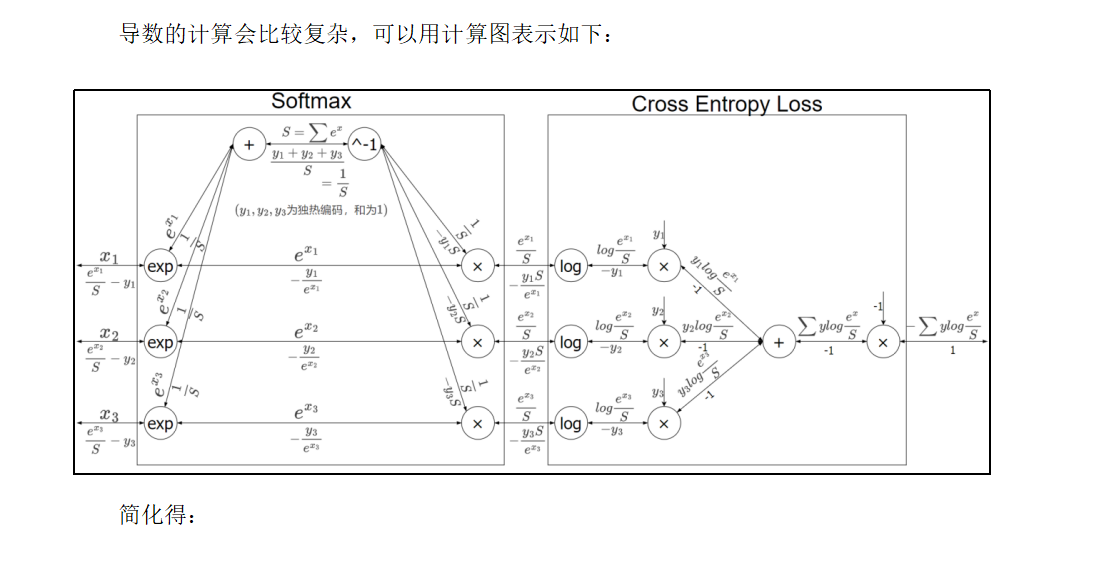
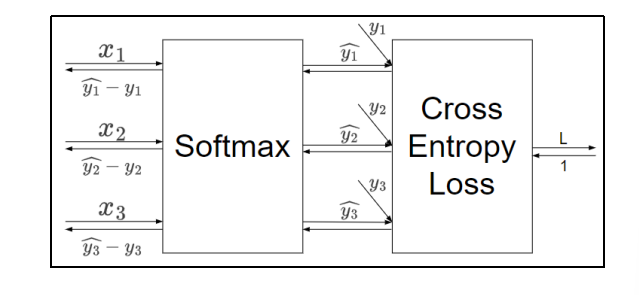
所以说这个损失函数Cross Entropy Loss就是为了softmax这个分类的函数专门设计的
回归问题的话，损失函数就是一个恒等函数，没有影响

class SoftmaxWithLoss:def __init__(self):self.loss = Noneself.y = None  # softmax的输出self.t = None  # 监督数据def forward(self, x, t):self.t = tself.y = softmax(x)self.loss = cross_entropy_error(self.y, self.t)return self.lossdef backward(self, dout=1):batch_size = self.t.shape[0]if self.t.size == self.y.size:  # 监督数据是one-hot-vector的情况dx = (self.y - self.t) / batch_sizeelse:dx = self.y.copy()dx[np.arange(batch_size), self.t] -= 1dx = dx / batch_sizereturn dx

总结