当前位置：首页 > news >正文

【Python】求解GPS未知及高斯噪声

news 2025/10/18 8:02:19

练习1：求解P点

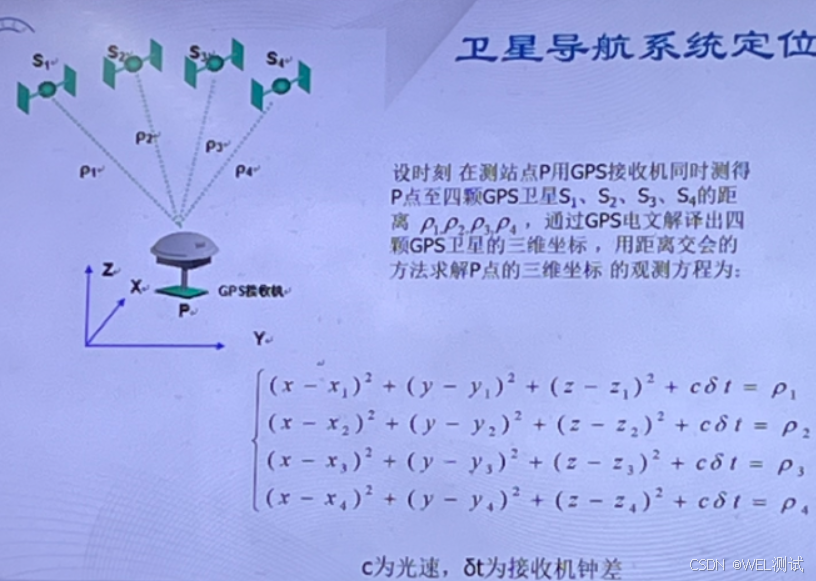
在这里插入图片描述

python编程源码

import numpy as np
from scipy.optimize import least_squaresdef residuals(x, satellites, distances, c):"""定义非线性方程组的残差（每个方程的“左边 - 右边”）x: 待求变量 [x, y, z, δt]satellites: 卫星坐标列表，每个元素为(xi, yi, zi)distances: 测量伪距列表 [ρ1, ρ2, ρ3, ρ4]c: 光速"""res = []for (sx, sy, sz), rho in zip(satellites, distances):# 计算球面方程的残差：(x-sx)² + (y-sy)² + (z-sz)² + c·δt - ρterm = (x[0]-sx)**2 + (x[1]-sy)** 2 + (x[2]-sz)** 2 + c * x[3]-rhores.append(term)return np.array(res)# ---------------------- 1. 输入已知数据 ----------------------
# 示例：4颗卫星的三维坐标（单位：米，实际由GPS电文提供）
satellites = [(15600000, 15600000, 20100000),   # 卫星S1坐标(18700000, 14600000, 18700000),   # 卫星S2坐标(17600000, 17600000, 19100000),   # 卫星S3坐标(19100000, 19100000, 18600000)    # 卫星S4坐标
]# 示例：测量得到的伪距（单位：米，实际由接收机测量）
distances = [20100000, 21200000, 21700000, 22200000]c = 299792458  # 光速（单位：m/s）# ---------------------- 2. 初始猜测值 ----------------------
# 初始值需尽量接近真实值（这里假设接收机在地面附近，钟差初始为0）
x0 = [0, 0, 0, 0]# ---------------------- 3. 求解非线性最小二乘问题 ----------------------
result = least_squares(residuals,          # 残差函数x0,                 # 初始猜测值args=(satellites, distances, c)  # 残差函数的额外参数
)# ---------------------- 4. 输出结果 ----------------------
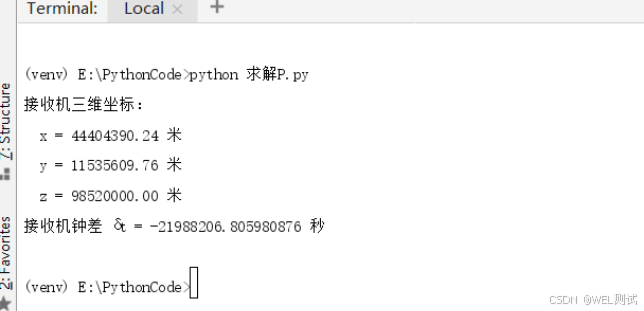
if result.success:x, y, z, dt = result.xprint(f"接收机三维坐标：")print(f"  x = {x:.2f} 米")print(f"  y = {y:.2f} 米")print(f"  z = {z:.2f} 米")print(f"接收机钟差 δt = {dt:.9f} 秒")
else:print("求解失败，原因：", result.message)

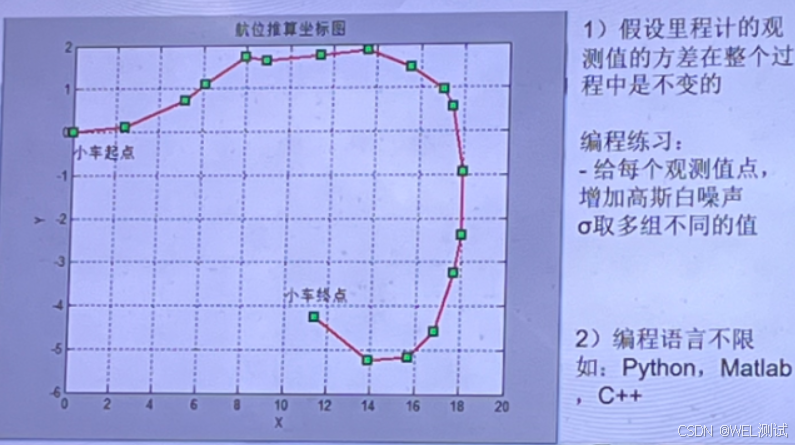
在这里插入图片描述

练习2：加噪声

在这里插入图片描述

问题1：航位退算坐标图python源码

import math
import matplotlib.pyplot as plt
# 指定Matplotlib使用系统中的中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 'SimHei'是黑体，你也可以尝试'SimSun'等
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号# 左轮和右轮单位时间内走过的距离（长度20）
Sr = [0, 3, 4, 2, 0, 0, 5, 0, 0, 2, 0, -4, 0, 0, 0, 0, 0, 0, 0, 0]
Sl = [0, 2, 2, 0, 5, 2, 0, 0, 5, 2, 3, 5, 3, 3, 2, 4, 3, 4, 5, 0]# 初始化参数（长度20，对应0-19时刻）
O = [0.0] * 20  # 小车相对于水平的角度（弧度）
X = [0.0] * 20  # 小车X坐标
Y = [0.0] * 20  # 小车Y坐标
L = 10  # 小车长度# 航位推算核心循环（Python中为0-18）
for i in range(19):# 计算下一时刻X坐标X[i+1] = X[i] + (Sr[i] + Sl[i]) * math.cos(O[i] + (Sr[i] - Sl[i])/(2 * L)) / 2# 计算下一时刻Y坐标Y[i+1] = Y[i] + (Sr[i] + Sl[i]) * math.sin(O[i] + (Sr[i] - Sl[i])/(2 * L)) / 2# 计算下一时刻角度O[i+1] = O[i] + (Sr[i] - Sl[i]) / L# 绘图
plt.figure(figsize=(8, 6))
plt.plot(X, Y, '-s',color='r',linewidth=2,markeredgecolor='k',markerfacecolor='g',markersize=8)# 添加图表元素
plt.grid(True)
plt.xlabel('X')
plt.ylabel('Y')
plt.text(0, -0.5, '小车起点')  # 起点坐标(0,0)
plt.text(10, -3.8, '小车终点') 
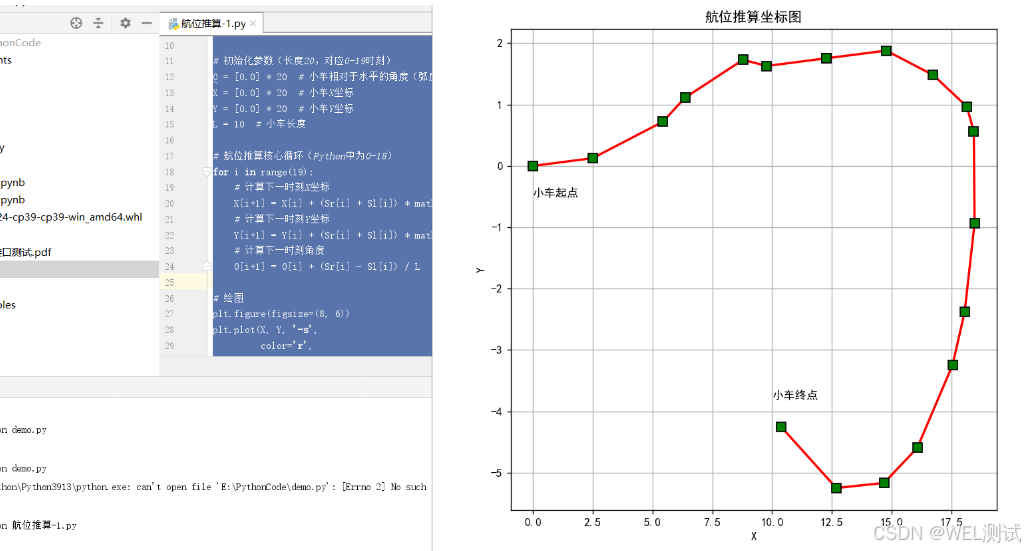
plt.title('航位推算坐标图')# 显示图像
plt.show()

代码运行效果截图：
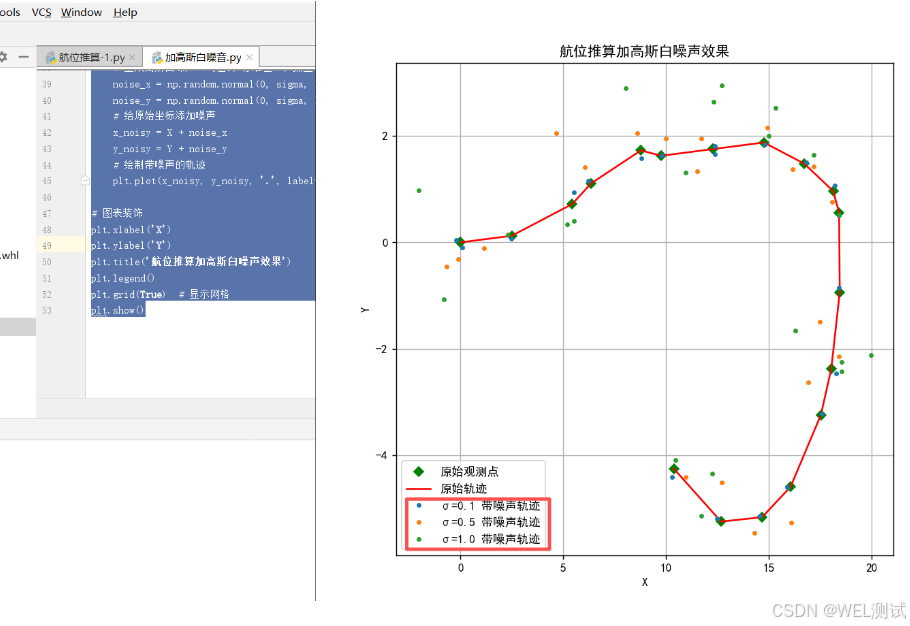
在这里插入图片描述

问题2：航位推算加高斯白噪声效果

import math
import matplotlib.pyplot as plt
import numpy as np
# 指定Matplotlib使用系统中的中文字体
plt.rcParams['font.sans-serif'] = ['SimHei']  # 'SimHei'是黑体，你也可以尝试'SimSun'等
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号# 左轮和右轮单位时间内走过的距离（长度20）
Sr = [0, 3, 4, 2, 0, 0, 5, 0, 0, 2, 0, -4, 0, 0, 0, 0, 0, 0, 0, 0]
Sl = [0, 2, 2, 0, 5, 2, 0, 0, 5, 2, 3, 5, 3, 3, 2, 4, 3, 4, 5, 0]# 初始化参数（长度20，对应0-19时刻）
O = [0.0] * 20  # 小车相对于水平的角度（弧度）
X = [0.0] * 20  # 小车X坐标
Y = [0.0] * 20  # 小车Y坐标
L = 10  # 小车长度# 定义多组不同的噪声标准差σ
sigma_values = [0.1, 0.5, 1.0]# 航位推算核心循环
for i in range(19):# 计算下一时刻X坐标X[i+1] = X[i] + (Sr[i] + Sl[i]) * math.cos(O[i] + (Sr[i] - Sl[i])/(2 * L)) / 2# 计算下一时刻Y坐标Y[i+1] = Y[i] + (Sr[i] + Sl[i]) * math.sin(O[i] + (Sr[i] - Sl[i])/(2 * L)) / 2# 计算下一时刻角度O[i+1] = O[i] + (Sr[i] - Sl[i]) / L# 创建画布
plt.figure(figsize=(10, 8))
# 绘制原始轨迹与观测点
plt.plot(X, Y, 'gD', label='原始观测点')  # 绿色方块：原始观测点
plt.plot(X, Y, 'r-', label='原始轨迹')    # 红色曲线：原始轨迹趋势# 对每组σ，添加噪声并绘制带噪声的轨迹
for sigma in sigma_values:# 生成高斯白噪声（均值0，标准差σ，数量与原始点一致）noise_x = np.random.normal(0, sigma, len(X))noise_y = np.random.normal(0, sigma, len(Y))# 给原始坐标添加噪声x_noisy = X + noise_xy_noisy = Y + noise_y# 绘制带噪声的轨迹plt.plot(x_noisy, y_noisy, '.', label=f'σ={sigma} 带噪声轨迹')# 图表装饰
plt.xlabel('X')
plt.ylabel('Y')
plt.title('航位推算加高斯白噪声效果')
plt.legend()
plt.grid(True)  # 显示网格
plt.show()