23ICPC杭州vp补题

原题链接
题解参考 1 2
感觉做起来很顺手，给我都打出拿牌幻想了（流泪

M 贪心

题意：给一个V图,求一个连续子序列平均值最大的V图
看样例发现选一边取到头，能达到最优，再从另外一边向外拓展

void solve(){int n;cin>>n;double ave=0;vector<int>a(n+1);int mn=1e9+10,mni=0;forr(i,1,n){cin>>a[i];if(a[i]<mn)mni=i,mn=a[i];}double lsm=0,rsm=0;double lc=mni+1,rc=n-mni+2;//选一边取到头forr(i,1,mni+1)lsm+=a[i];forr(i,mni-1,n)rsm+=a[i];ave=max(lsm/lc,rsm/rc);//另一边继续拓展reforr(l,1,mni-2)ave=max(ave,(rsm+a[l])/(rc+1)),rsm+=a[l],rc++;forr(r,mni+2,n)ave=max(ave,(lsm+a[r])/(lc+1)),lsm+=a[r],lc++;cout<<fixed<<setprecision(12)<<ave<<endl;
}

J 交互题 思维 图

题意：一棵树，可能是链或者菊花，每次询问一条边存在性，确定是链还是菊花。询问次数$\lceil \frac{n}{2}\rceil +3$
队友的思维成果。
从$\lceil \frac{n}{2}\rceil$想到可以问相邻数$(1,2),(3,4),(4,5)...$确定一部分链状

• 对于菊花图，所有其他点都连在一个点上，一定会有一个相邻数返回1
• 全答0，确定是像$2-3-1-4$这样的乱序链状
• 多个答1，确定不是菊花图，是链状

只答一个1有些扑朔迷离，使用另外三次询问次数确定

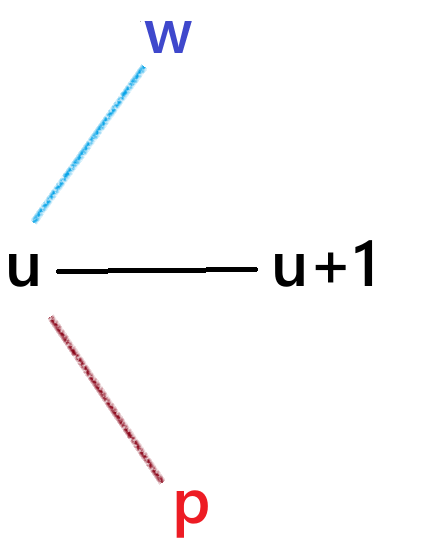
• 先询问唯一相连的$(u,u+1)$分别和w的连接性
  • 如果是菊花图，那么$(u,u+1)$其一是中心，w必和其中一个相连
  • 都不连，链
  • 和其中一个相连，再找一个p，看p是否也和那个疑似中心的相连，不相连就不是中心而是链
    

inline void ask(int a,int b){cout<<'?'<<' '<<(a)<<' '<<(b)<<endl;cout.flush();
}
inline void ans(int x){cout<<"! "<<x<<endl;cout.flush();}
void solve(){int n;cin>>n;int res=0;int cnt=0,u,v;//相邻问for(int i=1;i<n-1;i+=2){ask(i,i+1);cin>>res;if(res){u=i;break;}}if(!res){ask(n-1,n);cin>>res;if(res)u=n-1;}if(res){int w=(u==1?3:1);int p=(u==1?4:2);int tres;ask(u,w);cin>>res;//有一个相连 继续判断是不是菊花图if(res){ask(u,p);cin>>res;ans(res+1);return;}ask(u+1,w);cin>>res;if(res){ask(u+1,p);cin>>res;ans(res+1);return;}}ans(1);
}

D 构造

把中间的都构造成2-1=1

int main()
{int t,n,x,y,i;cin>>t;while(t--){cin>>n;//x=(2n-4+2y)/(1+(-1)^n*y)//注释是队友的思路 中间的和构造为-2+1=-1// if(n&1)// {//     x=-2*n;//     y=2;// }// else// {//     x=n-1;//     y=1;// }cout<<-2<<' ';for(i=1;i<n;i++)cout<<2<<' '<<-1<<' ';cout<<2*n<<endl;}return 0;
}

H 求期望 组合数学

题意： n 个数a1,a2…an，有 n 个事件，每个事件形如：如果 $a_i<a_{b_i}$，则$a_i=a_i+w_i$。事件随机顺序发生，问每个数的期望。

• 每个人糖的数量只有$a_i$、$a_i+w_i$两种情况，这两种情况的取舍只看$b_i$的糖数
• 如果$a_i<a_{b_i}$，一定能拿，$an{s}_i=a_i+w_i$
• $a_i>a_{b_i}+w_{b_i}$或者$i=b_i$，一定拿不了，$an{s}_i=a_i$
• $a_{b_i}\le a_i\le a_{b_i}+w_{b_i}$，如果$b_i$在$i$前面发生，那么$an{s}_i=a_i+w_i$，否则$an{s}_i=a_i$
  • 可以发现导致$an{s}_i=a_i+w_i$的前后顺序是一条长$d$的链，导致该情况的概率是$\frac{C_n^d\cdot (n-d)!}{n!}=\frac{1}{d!}$

const int N=5e5+5,mod=1e9+7,inf=1e9+10;
int fac[N],ifac[N];
int qpow(int a,int b){int res=1;for(;b;(a*=a)%=mod,b>>=1)if(b&1)(res*=a)%=mod;return res%mod;
}
int inv(int x){return qpow(x,mod-2)%mod;
}
void init(){fac[0]=1;forr(i,1,N-2){fac[i]=(fac[i-1]*i)%mod;}ifac[N-2]=inv(fac[N-2]);reforr(i,1,N-3){ifac[i]=(ifac[i+1]*(i+1))%mod;}
}
vector<int>e[N];
int dep[N];
void dfs(int now){for(auto x:e[now]){dep[x]=dep[now]+1;dfs(x);}
}
int C(int n,int m){if(n==m)return 1;if(n<m)return 0;return (fac[n]*ifac[n-m]%mod*ifac[m]%mod)%mod;
}
void solve(){int n;cin>>n;forr(i,1,n)e[i].clear(),dep[i]=0;vector<int>a(n+1),b(n+1),w(n+1),st(n+1,0);vector<int>ans(n+1);forr(i,1,n)cin>>a[i];forr(i,1,n)cin>>b[i];forr(i,1,n)cin>>w[i];forr(i,1,n){if(a[i]<a[b[i]])st[i]=1,ans[i]=(a[i]+w[i])%mod,dep[i]=1;//先后发生会有不一样的结果else if(a[b[i]]+w[b[i]]<=a[i])st[i]=1,ans[i]=a[i]%mod,dep[i]=0;//不会增加 先发生后发生都一样if(i==b[i])st[i]=1,ans[i]=a[i]%mod,dep[i]=0;}forr(i,1,n){if(st[i])continue;e[b[i]].push_back(i);}forr(i,1,n){if(st[i]&&dep[i])dfs(i);}forr(i,1,n){if(st[i])continue;// int gt=fac[n-dep[i]]*C(n,dep[i])%mod;// (ans[i]+=(a[i]+w[i])%mod*gt%mod*ifac[n]%mod)%=mod;// (ans[i]+=a[i]*((fac[n]-gt+mod)%mod)%mod*ifac[n]%mod)%mod;else ans[i]=(a[i]+w[i]*ifac[dep[i]]%mod)%mod;}forr(i,1,n)cout<<ans[i]%mod<<' ';cout<<endl;
}
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int _=1;init();cin>>_;while (_--){solve();}return 0;
}

G 最短路 堆优化Dij

题意：给定n×m地图上的一条长度为k的贪吃蛇。每次操作可以控制贪吃蛇移动一步或者缩短一格蛇身。对于每个位置，求从初始状态出发最少需要多少次操作使得蛇头到达该处。

每个操作都可以等价看作初始蛇身必然缩短1，并且同时控制蛇头移动一步或者不移动，因此蛇头到达每个位置的时间越早越好。

const int N=3e3+5,mod=1e9+7,inf=0x3f3f3f3f3f3f3f3f;
int fg[N][N],dis[N][N],vis[N][N];
string s[N];
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
void solve(){int n,m,k;cin>>n>>m>>k;memset(dis,0x3f,sizeof dis);priority_queue<piii,vector<piii>,greater<piii>>q;forr(i,1,k){int x,y;cin>>x>>y;fg[x][y]=k-i;//这个点还剩多长时间能用if(i==1){q.push({0,{x,y}});dis[x][y]=0;}}forr(i,1,n){cin>>s[i];s[i]=' '+s[i];}while (q.size()){auto [d,p]=q.top();q.pop();auto [x,y]=p;if(vis[x][y])continue;vis[x][y]=1;forr(i,0,3){int nx=x+dx[i],ny=y+dy[i];if(nx<1||nx>n||ny<1||ny>m||s[nx][ny]=='#'||vis[nx][ny])continue;int nd=max(fg[nx][ny]+1,dis[x][y]+1);//fg[nx][ny]是需要缩短蛇身或蛇头向前移动（这两种操作等价，都能让被占据的地方尽快能让开）if(dis[nx][ny]>nd){dis[nx][ny]=nd;q.push({nd,{nx,ny}});}}}unsigned int ans=0;forr(i,1,n){forr(j,1,m){if(dis[i][j]<inf)ans+=dis[i][j]*dis[i][j];}}cout<<ans<<endl;
}