数据结构——二十一、哈夫曼树(王道408)
文章目录
- 前言
- 一.带权路径长度
- 1.带权路径长度及相关概念
- 2.计算实例
- 二.哈夫曼树
- 1.哈夫曼树的定义
- 2.哈夫曼树的构造
- 1.总体方法
- 2.具体例子
- 3.哈夫曼树的性质
- 三.哈夫曼树的经典应用(哈夫曼编码)
- 1.固定长度编码
- 1.定义
- 2.例子
- 2.可变长度编码(哈夫曼编码)
- 1.定义
- 2.例子
- 3.相关概念
- 4.哈夫曼编码的应用
- 1.例子
- 四.知识回顾与重要考点
- 结语
前言
文章摘要
本文系统介绍了哈夫曼树及其应用。首先定义了带权路径长度(WPL)的计算方法,通过实例比较不同二叉树的WPL值。重点阐述哈夫曼树的构造算法:每次合并权值最小的两棵树,最终生成WPL最小的最优二叉树,其具有结点总数2n-1、无度为1结点等特点。经典应用为哈夫曼编码,通过将高频字符分配短编码实现数据压缩,相比固定长度编码可显著减少传输位数。文中还通过字母频率统计案例,展示了哈夫曼编码实现59.71%压缩率的过程,并强调前缀编码的无歧义特性。最后总结了哈夫曼树的核心考点,包括构造步骤、性质及编码应用。
代码在文章开头部分,需要自取🧐
哈夫曼树
一.带权路径长度
1.带权路径长度及相关概念
- 结点的权:有某种现实含义的数值(如:表示结点的重要性等)
- 结点的带权路径长度:从树的根到该结点的路径长度(经过的边数)与该结点上权值的乘积
- 树的带权路径长度:树中所有叶结点的带权路径长度之和(WPL, Weighted Path Length)
WPL=∑i=1nwiliWPL=\sum_{i=1}^{n}w_{i}l_{i}WPL=i=1∑nwili
2.计算实例
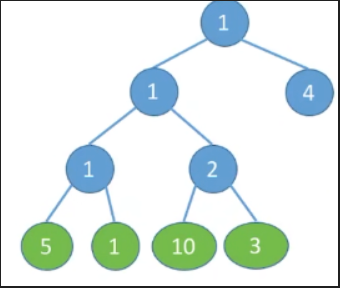
-
图一
-
WPL=2∗1+2∗3+2∗4+2∗5=26WPL=2*1+2*3+2*4+2*5=26WPL=2∗1+2∗3+2∗4+2∗5=26
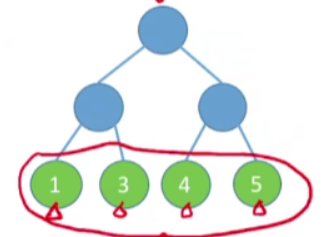
-
图二
-
WPL=1∗5+2∗4+3∗1+3∗3=25WPL=1*5+2*4+3*1+3*3=25WPL=1∗5+2∗4+3∗1+3∗3=25
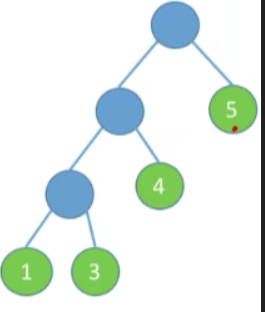
-
图三
-
WPL=1∗5+2∗4+3∗1+3∗3=25WPL=1*5+2*4+3*1+3*3=25WPL=1∗5+2∗4+3∗1+3∗3=25
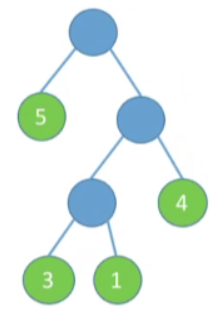
-
图四
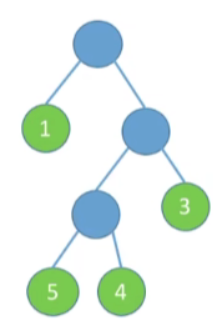
-
WPL=1∗1+2∗3+3∗5+3∗4=34WPL=1*1+2*3+3*5+3*4=34WPL=1∗1+2∗3+3∗5+3∗4=34
二.哈夫曼树
1.哈夫曼树的定义
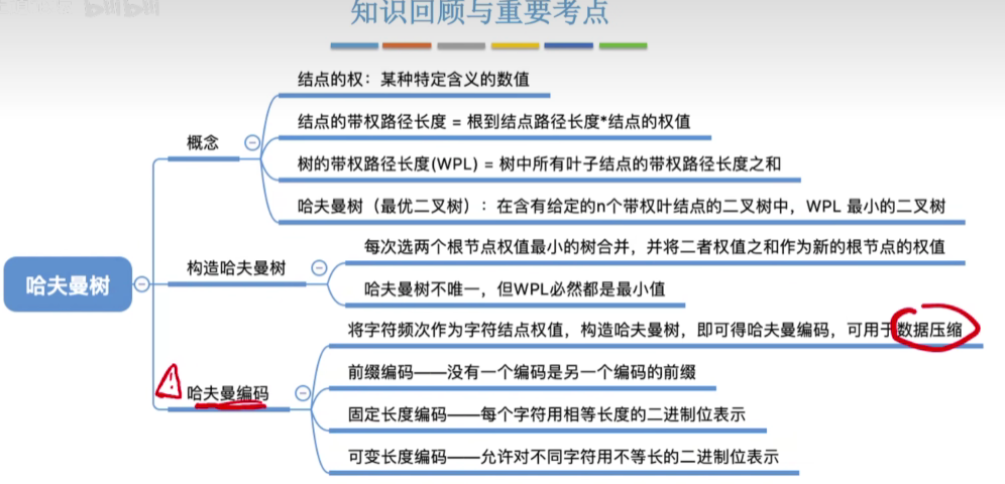
- 在含有n个带权叶结点的二叉树中,其中带权路径长度(WPL)最小的二叉树称为哈夫曼树,也称最优二叉树
2.哈夫曼树的构造
1.总体方法
- 给定 n 个权值分别为 w1,w2,…,wnw_{1},w_{2},\dotsc ,w_{n}w1,w2,…,wn 的结点,构造哈夫曼树的算法描述如下:
- 将这 n 个结点分别作为 n 棵仅含一个结点的二叉树,构成森林 F。
- 构造一个新结点,从 F 中选取两棵根结点权值最小的树作为新结点的左、右子树,并且将新结点的权值置为左、右子树上根结点的权值之和。
- 从 F 中删除刚才选出的两棵树,同时将新得到的树加入 F 中。
- 重复步骤 2 和 3,直至 F 中只剩下一棵树为止。
2.具体例子
- 将下图几个结点组成哈夫曼树,结点下的数字为其权值
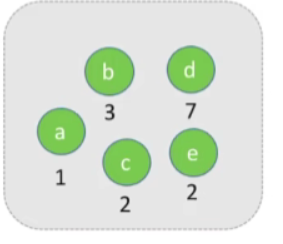
-
我们每一次要从这个集合当中选择两个权值最小的节点,让他们俩成为兄弟,这个例子中,我们可以选择权值最小的a节点和c节点,并且把刚刚选择的两个节点(也就是a和c结点)的权值之和作为这棵新树的根节点的权值
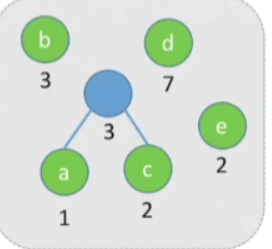
-
接下来做的事情是一样的,接着选择两个根节点的权值最小的两棵树让他们成为兄弟,这里我们可以选择e和刚才新生成的这棵树(当然你也可以选择e和b先结合)
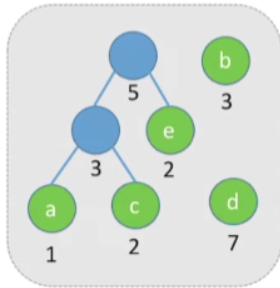
-
接下来操作与之前一样,不做赘述,最终结果如图
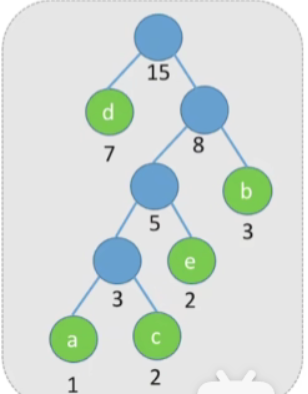
- 最终计算得出WPLmin=1∗7+2∗3+3∗2+4∗1+4∗2=31WPL_{\text{min}}=1*7+2*3+3*2+4*1+4*2=31WPLmin=1∗7+2∗3+3∗2+4∗1+4∗2=31
3.哈夫曼树的性质
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大
- 总共n个节点,我们要两两结合,让它们合并成一棵树,所以我们总共需要合并n-1次,每一次合并都会导致会增加一个分支节点,因此哈夫曼树的结点总数为2n-1
- 哈夫曼树中不存在度为1的结点
- 哈夫曼树并不唯一,但WPL必然相同且为最优
-
如刚刚的例子也可以构造出如下图的哈夫曼树
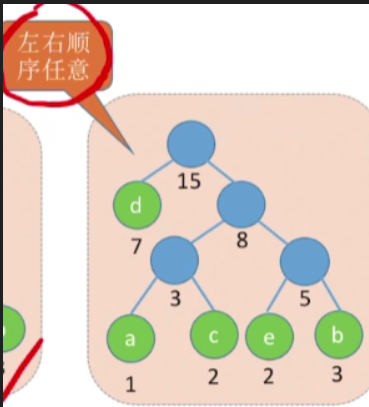
-
WPL=1∗7+3∗(1+2+2+3)=31WPL=1*7+3*(1+2+2+3)=31WPL=1∗7+3∗(1+2+2+3)=31
-
三.哈夫曼树的经典应用(哈夫曼编码)
补充小知识:电报——点、划两个信号(二进制0/1),接收电报或者窃听电报的人只需要把这些点和划的信息翻译成有意义的字符就可以了
1.固定长度编码
1.定义
- 固定长度编码——每个字符用相等长度的二进制位表示(如ASCII编码)
2.例子
- 每个字符用长度为2的二进制表示
- 假设要表示100个字符,其中80个字符为C,10个字符为A,8个字符为B,2个字符为D
| 字符 | A | B | C | D |
|---|---|---|---|---|
| 编码 | 00 | 01 | 10 | 11 |
-
所有字符的二进制长度=80∗2+10∗2+8∗2+2∗2=20080*2+10*2+8*2+2*2=20080∗2+10∗2+8∗2+2∗2=200 bit
-
用树表示
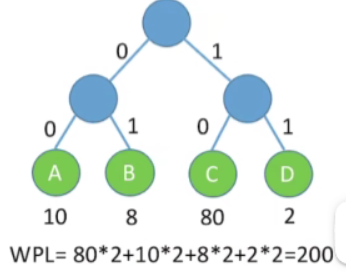
-
WPL=80∗2+10∗2+8∗2+2∗2=200WPL=80*2+10*2+8*2+2*2=200WPL=80∗2+10∗2+8∗2+2∗2=200
-
可以发现:刚才我们计算最终发送的这个二进制码的长度,其实就是计算了这棵树的一个带权路径长度
2.可变长度编码(哈夫曼编码)
1.定义
- 可变长度编码——允许对不同字符用不等长的二进制位表示
- 有哈夫曼树得到哈夫曼编码——字符集中的每个字符作为一个叶子结点,各个字符出现的频度作为结点的权值,根据之前介绍的方法构造哈夫曼树
- 哈夫曼编码就是一种可变长度编码
- 哈夫曼树不唯一,因此哈夫曼编码不唯一
2.例子
-
为了优化最终发送的二进制码的长度,我们可以采用将其转化为哈夫曼树的方法得到长度最优的编码方式
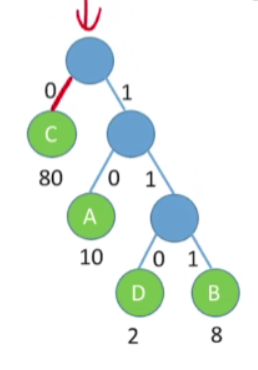
-
最终得到的四个字母的编码方案
| 字母 | A | B | C | D |
|---|---|---|---|---|
| 编码 | 10 | 111 | 0 | 110 |
- 这个编码方案发送100个字符的二进制长度,也就是这棵树的带权路径长度为WPL=80∗1+10∗2+2∗3+8∗3=130WPL=80*1+10*2+2*3+8*3=130WPL=80∗1+10∗2+2∗3+8∗3=130
3.相关概念
- 若没有一个编码是另一个编码的前缀,则称这样的编码为前缀编码
- 前缀码解码无歧义是一种不会出现歧义的编码方式
4.哈夫曼编码的应用
- 哈夫曼编码可用于数据压缩
1.例子
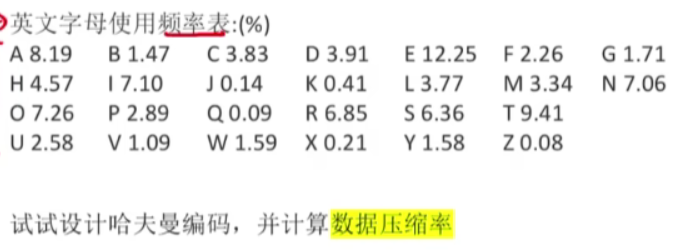
- 将每个字符视为一个节点,按频率从小到大排序。重复合并频率最小的两个节点,形成新节点,直到只剩一个根节点。分配编码时,左分支为0,右分支为1。
- 从根节点到每个叶节点的路径生成编码。
- 基于上述过程,得到的编码表如下(编码为二进制字符串):
| 字符 | 频率 (%) | 哈夫曼编码 | 字符 | 频率 (%) | 哈夫曼编码 | 字符 | 频率 (%) | 哈夫曼编码 |
|---|---|---|---|---|---|---|---|---|
| E | 12.25 | 010 | D | 3.91 | 111101 | P | 2.89 | 01111 |
| T | 9.41 | 000 | L | 3.77 | 110010 | B | 1.47 | 100100 |
| A | 8.19 | 11100 | C | 3.83 | 111100 | V | 1.09 | 001101 |
| O | 7.26 | 11000 | U | 2.58 | 01110 | K | 0.41 | 0011000 |
| I | 7.10 | 10111 | M | 3.34 | 10011 | J | 0.14 | 001100110 |
| N | 7.06 | 10110 | W | 1.59 | 1100110 | X | 0.21 | 00110010 |
| S | 6.36 | 0110 | F | 2.26 | 001111 | Q | 0.09 | 0011001111 |
| R | 6.85 | 10000 | G | 1.71 | 1100111 | Z | 0.08 | 0011001110 |
| H | 4.57 | 00110 | Y | 1.58 | 100101 |
- 假设每个字符使用8位ASCII编码,平均码长为8位
- 根据哈夫曼编码和频率计算加权平均码长:
- 计算公式:平均码长 = ∑(频率 × 码长) / 100
- 计算过程:根据上表,∑(频率 × 码长) = 477.69
- 平均码长 = 477.69 / 100 = 4.7769 位
- 数据压缩率:压缩后大小与原始大小之比
- 压缩率 = 平均码长 / 原始码长 = 4.7769 / 8 ≈ 0.5971
- 即压缩率为59.71%,表示压缩后数据大小约为原始数据的59.71%。
四.知识回顾与重要考点
结语
一更😉
如果想要看更多章节,请点击一、数据结构专栏导航页
