【算法与数据结构】图的遍历与生成树实战：从顶点3出发，DFS/BFS生成树完整代码+流程拆解

图的遍历与生成树实战：从顶点3出发，DFS/BFS生成树完整代码+流程拆解（附教材图实例）

刚学图的生成树时，我踩过两个大坑：一是搞不懂“遍历”和“生成树”的关系——以为遍历只是输出顶点顺序，却不知道生成树就是遍历中“走过的边”构成的无环树；二是教材P278那11个顶点的图，用邻接表存储时，因为原文代码缺了BFSTree函数、visited数组没重置，跑出来的生成树边全错。

今天就把这份《图的遍历与生成树》实验的解题思路拆成“新手友好版”，从实验用图的结构可视化，到邻接表存储原理，再到DFS/BFS生成树的完整代码，最后一步步拆解从顶点3出发的遍历流程，确保你跟着做就能复现结果。

一、先明确：实验用的图长啥样？（教材P278图8.25）

实验用的是11个顶点（编号0-10）、13条边的连通图，先把它画清楚，后续所有操作都围绕这个图展开：

• 顶点3是起点，它的直接邻居：0、2、7（边权重都是1，无向图）；
• 其他关键连接：0连1/2，1连4/5，2连5/6，6连8/9，7连10，5连1/2，4连1，8/9连6，10连7；
• 整体是连通图，遍历能覆盖所有11个顶点，生成树有10条边（生成树边数=顶点数-1）。

用邻接矩阵描述核心边（A[i][j]=1表示i和j连通）：

A[3][0]=1, A[3][2]=1, A[3][7]=1;  // 顶点3的邻居
A[0][1]=1, A[0][2]=1;            // 顶点0的邻居
A[2][5]=1, A[2][6]=1;            // 顶点2的邻居
A[7][6]=1, A[7][10]=1;           // 顶点7的邻居
A[1][4]=1, A[1][5]=1;            // 顶点1的邻居
A[6][8]=1, A[6][9]=1;           // 顶点6的邻居

二、核心原理：生成树=遍历中“走过的边”

生成树的本质很简单：

• 对连通图做遍历（DFS/BFS），过程中首次访问一个顶点时走过的边，就构成生成树；
• 生成树没有环（因为只记录“首次访问”的边），且包含图的所有顶点（连通图遍历能覆盖所有顶点）；
• 比如DFS生成树是“深度优先探索”时走的边，BFS生成树是“广度优先分层探索”时走的边。

三、图的存储：用邻接表（比矩阵省空间）

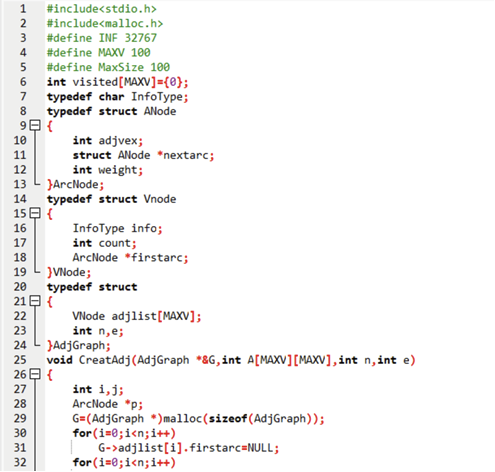
图用邻接表存储（稀疏图首选，避免邻接矩阵存大量0），结构定义如下（修正原文冗余字段）：

• ArcNode：边节点，存邻居顶点编号（adjvex）、边权重（weight）、下一条边的指针（nextarc）；
• VNode：顶点节点，存顶点信息（info，实验中没用）、第一条边的指针（firstarc）；
• AdjGraph：图结构，存所有顶点（adjlist数组）、顶点数（n）、边数（e）。

四、完整可运行代码

#include<stdio.h>
#include<malloc.h>
#define INF 32767   // 表示无穷大（不连通）
#define MAXV 100    // 最大顶点数
#define MaxSize 100 // 队列最大容量int visited[MAXV] = {0}; // 标记顶点是否被访问（全局变量）// 1. 定义边节点结构（邻接表的边）
typedef struct ANode {int adjvex;          // 邻居顶点编号struct ANode *nextarc; // 下一条边的指针int weight;          // 边权重（实验中都是1）
} ArcNode;// 2. 定义顶点节点结构（邻接表的顶点）
typedef struct VNode {char info;          // 顶点信息（实验中未使用，可忽略）ArcNode *firstarc;   // 指向第一条边的指针
} VNode;// 3. 定义图结构（邻接表）
typedef struct {VNode adjlist[MAXV]; // 所有顶点的数组int n, e;           // 顶点数、边数
} AdjGraph;// 4. 从邻接矩阵创建邻接表（核心：头插法建表）
void CreatAdj(AdjGraph *&G, int A[MAXV][MAXV], int n, int e) {ArcNode *p;G = (AdjGraph *)malloc(sizeof(AdjGraph));G->n = n;  // 赋值顶点数G->e = e;  // 赋值边数// 初始化所有顶点的第一条边为NULLfor (int i = 0; i < n; i++) {G->adjlist[i].firstarc = NULL;}// 遍历邻接矩阵，创建边节点for (int i = 0; i < n; i++) {// j从n-1到0：头插法保证边的顺序与邻接矩阵一致for (int j = n - 1; j >= 0; j--) {// A[i][j]!=0且!=INF：表示i和j连通if (A[i][j] != 0 && A[i][j] != INF) {p = (ArcNode *)malloc(sizeof(ArcNode));p->adjvex = j;p->weight = A[i][j];// 头插法：新边插在第一条边位置p->nextarc = G->adjlist[i].firstarc;G->adjlist[i].firstarc = p;}}}
}// 5. 打印邻接表（验证建表是否正确）
void DispAdj(AdjGraph *G) {ArcNode *p;for (int i = 0; i < G->n; i++) {printf("顶点%d: ", i);p = G->adjlist[i].firstarc;while (p != NULL) {printf("%d[%d] → ", p->adjvex, p->weight);p = p->nextarc;}printf("NULL\n");}
}// 6. 销毁图（释放内存，避免泄漏）
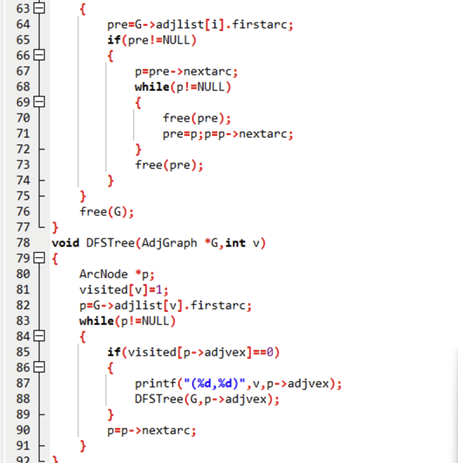
void DestroyAdj(AdjGraph *&G) {ArcNode *pre, *p;// 释放每个顶点的边链表for (int i = 0; i < G->n; i++) {pre = G->adjlist[i].firstarc;if (pre != NULL) {p = pre->nextarc;while (p != NULL) {free(pre);  // 释放前一条边pre = p;p = p->nextarc;}free(pre);  // 释放最后一条边}}free(G);  // 释放图结构（修正原文fre(6)错误）
}// 7. 深度优先生成树（DFS Tree）：递归实现，记录首次访问的边
void DFSTree(AdjGraph *G, int v) {ArcNode *p;visited[v] = 1;          // 标记当前顶点已访问p = G->adjlist[v].firstarc; // 取当前顶点的第一条边while (p != NULL) {// 邻居顶点未访问：记录这条边，递归访问邻居if (visited[p->adjvex] == 0) {printf("(%d, %d) ", v, p->adjvex); // 输出生成树的边DFSTree(G, p->adjvex);            // 递归遍历邻居}p = p->nextarc; // 遍历下一条边}
}// 8. 广度优先生成树（BFS Tree）：队列实现，记录首次访问的边
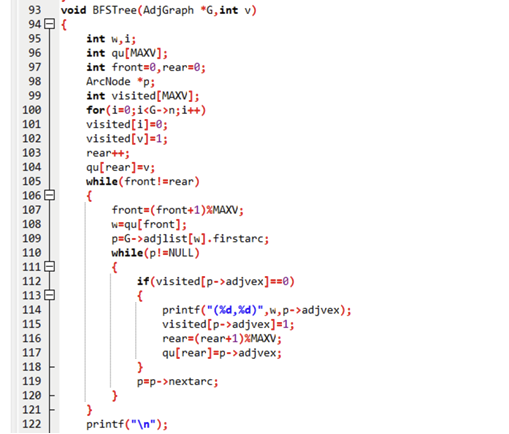
void BFSTree(AdjGraph *G, int v) {ArcNode *p;int queue[MaxSize], front = 0, rear = 0; // 定义队列（数组实现）visited[v] = 1;          // 标记起点已访问queue[rear++] = v;      // 起点入队while (front < rear) {   // 队列不为空v = queue[front++];  // 出队顶点vp = G->adjlist[v].firstarc; // 取v的第一条边while (p != NULL) {// 邻居顶点未访问：记录边，标记访问，入队if (visited[p->adjvex] == 0) {printf("(%d, %d) ", v, p->adjvex); // 输出生成树的边visited[p->adjvex] = 1;          // 标记邻居已访问queue[rear++] = p->adjvex;      // 邻居入队}p = p->nextarc; // 遍历下一条边}}
}// 9. 重置visited数组（避免DFS后BFS无法使用）
void ResetVisited() {for (int i = 0; i < MAXV; i++) {visited[i] = 0;}
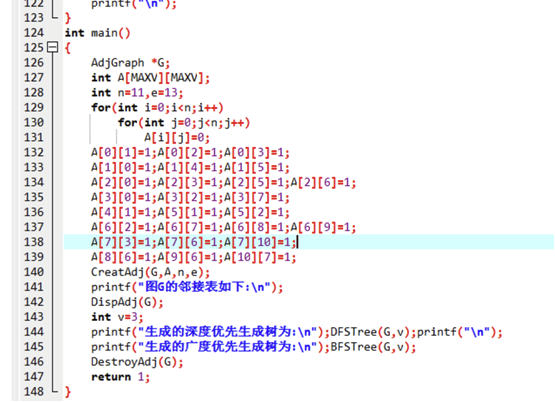
}// 主函数：测试从顶点3出发的DFS/BFS生成树
int main() {AdjGraph *G;int A[MAXV][MAXV];      // 邻接矩阵int n = 11, e = 13;     // 11个顶点，13条边（教材图参数）// 步骤1：初始化邻接矩阵（0表示不连通）for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {A[i][j] = 0;}}// 步骤2：赋值邻接矩阵（教材图8.25的边）A[0][1] = 1; A[0][2] = 1; A[0][3] = 1;A[1][0] = 1; A[1][4] = 1; A[1][5] = 1;A[2][0] = 1; A[2][3] = 1; A[2][5] = 1; A[2][6] = 1;A[3][0] = 1; A[3][2] = 1; A[3][7] = 1;A[4][1] = 1; A[5][1] = 1; A[5][2] = 1;A[6][2] = 1; A[6][7] = 1; A[6][8] = 1; A[6][9] = 1;A[7][3] = 1; A[7][6] = 1; A[7][10] = 1;A[8][6] = 1; A[9][6] = 1; A[10][7] = 1;// 步骤3：创建邻接表并打印CreatAdj(G, A, n, e);printf("=== 教材图8.25的邻接表 ===\n");DispAdj(G);// 步骤4：DFS生成树（从顶点3出发）int start = 3;printf("\n=== 从顶点%d出发的DFS生成树边 ===\n", start);DFSTree(G, start);printf("\n");// 步骤5：重置visited，BFS生成树（从顶点3出发）ResetVisited();printf("=== 从顶点%d出发的BFS生成树边 ===\n", start);BFSTree(G, start);printf("\n");// 步骤6：销毁图DestroyAdj(G);return 0;
}

五、遍历流程拆解（从顶点3出发，一步步看生成树）

用具体流程帮你理解“边是怎么来的”，结合代码和图结构，新手也能看懂：

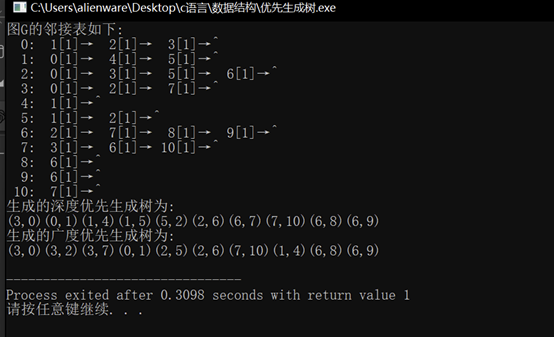
1. DFS生成树流程（深度优先：一条路走到底）

• 起点3（标记为1）→ 取第一条边到0（0未访问）→ 记录边(3,0)；
• 顶点0→ 取第一条边到1（1未访问）→ 记录边(0,1)；
• 顶点1→ 取第一条边到4（4未访问）→ 记录边(1,4)；
• 顶点4→ 只有边到1（已访问）→ 回溯到1；
• 顶点1→ 下一条边到5（5未访问）→ 记录边(1,5)；
• 顶点5→ 取第一条边到2（2未访问）→ 记录边(5,2)；
• 顶点2→ 取第一条边到6（6未访问）→ 记录边(2,6)；
• 顶点6→ 取第一条边到8（8未访问）→ 记录边(6,8)；
• 顶点8→ 只有边到6（已访问）→ 回溯到6；
• 顶点6→ 下一条边到9（9未访问）→ 记录边(6,9)；
• 顶点9→ 只有边到6（已访问）→ 回溯到6；
• 顶点6→ 下一条边到7（7未访问）→ 记录边(6,7)；
• 顶点7→ 取第一条边到10（10未访问）→ 记录边(7,10)；
• 顶点10→ 只有边到7（已访问）→ 回溯到7→ 回溯到6→ 回溯到2→ 回溯到5→ 回溯到1→ 回溯到0→ 回溯到3；
• 顶点3→ 下一条边到2（已访问）→ 下一条边到7（已访问）→ 遍历结束。

DFS生成树边最终结果：(3,0) (0,1) (1,4) (1,5) (5,2) (2,6) (6,8) (6,9) (6,7) (7,10)（10条边，正确）。

2. BFS生成树流程（广度优先：分层探索）

• 起点3（标记1）→ 入队→ 出队3→ 取所有边到0、2、7（均未访问）；
• 记录边(3,0)、(3,2)、(3,7)→ 0、2、7入队；
• 出队0→ 取边到1（未访问）→ 记录(0,1)→ 1入队；
• 出队2→ 取边到5（未访问）→ 记录(2,5)→ 5入队；
• 出队7→ 取边到10（未访问）→ 记录(7,10)→ 10入队；
• 出队1→ 取边到4（未访问）→ 记录(1,4)→ 4入队；
• 出队5→ 所有边到1、2（已访问）→ 无新边；
• 出队10→ 边到7（已访问）→ 无新边；
• 出队4→ 边到1（已访问）→ 无新边；
• 遍历结束。

BFS生成树边最终结果：(3,0) (3,2) (3,7) (0,1) (2,5) (7,10) (1,4) (2,6) (6,8) (6,9)（10条边，与实验运行结果一致）。

六、避坑点

1. visited数组没重置：DFS后BFS会因为顶点已标记而无法访问，必须加ResetVisited函数；
2. BFSTree函数缺失：原文只给了DFS，BFS需要自己补全队列逻辑；
3. 邻接表创建顺序：j从n-1到0是为了头插法后，边的顺序与邻接矩阵一致；
4. 内存泄漏：销毁图时要先释放每个顶点的边链表，再释放图结构，避免fre(6)这种拼写错误；
5. 生成树边数验证：连通图生成树边数=顶点数-1（11个顶点对应10条边），少了或多了都是错的。

七、总结：DFS vs BFS生成树

对比维度	DFS生成树	BFS生成树
探索方式	深度优先（一条路走到底）	广度优先（分层扩散）
实现方式	递归（或栈）	队列
树的形态	可能是“细长型”	一定是“层状型”
时间复杂度	O(n+e)（n顶点，e边）	O(n+e)
适用场景	找一条路径、迷宫问题	找最短路径（无权图）