数值计算-例题
线性方程组的直接解法
A. 消元/分解类(直接法)
高斯消元(Gaussian Elimination)
本质:前向消元 + 回代;等价于做 LU 分解。
主元策略:
不选主元:快,但可能不稳(遇零/极小主元会炸)。
部分选主元(默认推荐):每列选最大者换行,稳且代价低;得到 (PA=LU)。
完全选主元:行列都换,更稳但更慢。
适用:通用方阵。
Python:
np.linalg.solve(A,b)(内部即 LU+部分主元)。
LU 分解(带主元)
本质:(PA=LU);一次分解,多次前/回代解不同右端。
适用:同一 (A) 多个 (b)。
稳定性:部分选主元稳健。
Python:
一次性:
np.linalg.solve(A,b)复用版:
scipy.linalg.lu_factor(A)→scipy.linalg.lu_solve((lu,piv), b)教学拆解:
scipy.linalg.lu(A)+solve_triangular(...)
Cholesky 分解(
)
本质:SPD 矩阵的“平方根”分解;存储/计算约为 LU 的一半。
适用:**对称正定(SPD)**最优选择,快且稳;不需主元。
Python:
scipy.linalg.cho_factor/cho_solve或np.linalg.cholesky + solve_triangular
LDLᵀ 分解
本质:对称矩阵通用分解 (
);SPD 时 (D) 对角元全正,可转为 Cholesky。
适用:对称(含不定)问题;不定时常配 Bunch–Kaufman 枢轴。
Python:
scipy.linalg.ldl(较新版本提供)+solve_triangular
QR 分解 / 最小二乘(LS)
本质:(A=QR),解超定或病态方程的 LS;比 LU 更适合最小二乘。
适用:超定系统、拟合、近奇异下的 LS。
Python:
np.linalg.lstsq(A,b),或scipy.linalg.qr系列
B. 迭代/预条件
共轭梯度 CG / 预条件共轭梯度 PCG
本质:迭代法;对 SPD 大规模稀疏矩阵高效。
预条件:常配 不完全 Cholesky (IC) 等,显著加速。
适用:超大规模 SPD(直接法成本/内存高时)。
Python:
scipy.sparse.linalg.cg(如需)
C. 数值策略与配套概念
主元选择(Pivoting)
不选主元:可能不稳;
部分选主元(工程默认):稳健且便宜;
完全选主元:最稳更慢。
→ 我们在第 7、8 题实际都用“带部分选主元的高斯消元”。
条件数 (
)
定义:
(用同一向量范数诱导的矩阵范数)。
解释:误差放大倍数;(\kappa) 越大越病态。
Hilbert 矩阵:
)—— 随 (n) 指数级爆炸。
误差 vs 残差
残差小((
) 小)≠ 误差小;病态矩阵可使小残差对应大求解误差。
D. 何时选用哪种方法
SPD:Cholesky(
cho_factor/cho_solve)> LU。一般方阵:LU(部分主元)(
solve或lu_factor/lu_solve)。最小二乘/超定/近奇异:QR /
lstsq。同一 (A) 多 RHS:先分解(LU/Cholesky),多次前/回代。
大稀疏 SPD:CG/PCG。
极病态(如 Hilbert):任何双精度直接法都会失准;若必须高精度,考虑多重精度库或正则化/重缩放/预条件。

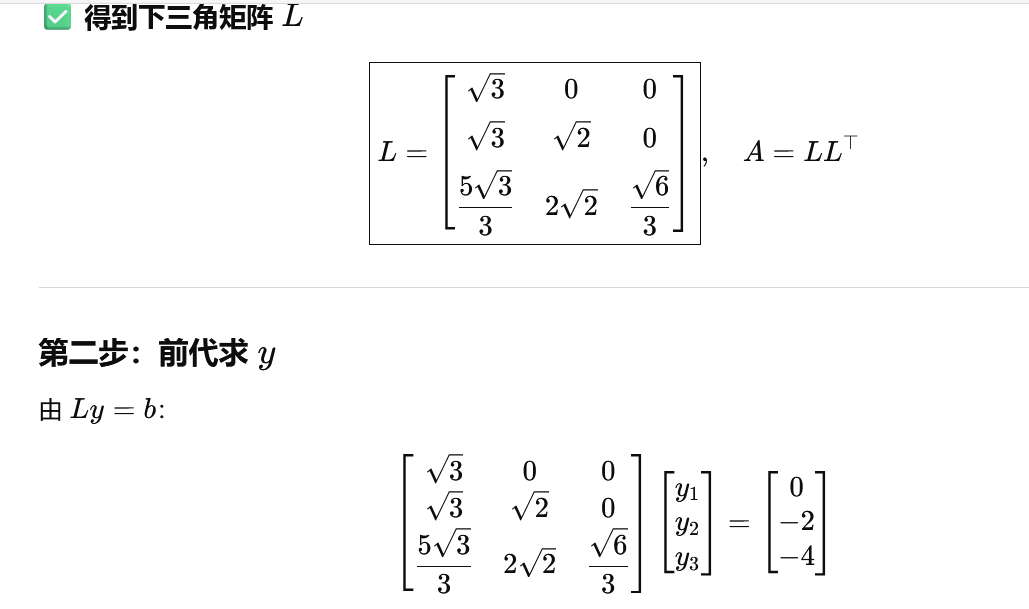
例题



这里与原来LU分解的区别是,可以交换主元;保存P矩阵的目的就是为了记录交换行的情况



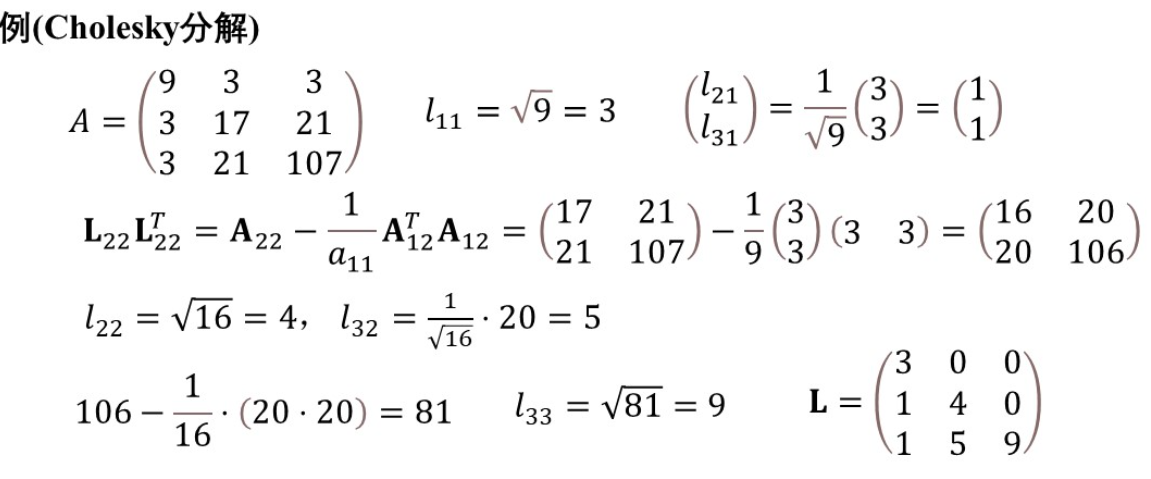
继续求解LU示例