整型数据与浮点型数据在内存中的存储方法

1、整型数据在内存中的存储方法

以int类型数据为例，整型数据在内存中以二进制序列的形式存储。

1.1、原码、反码、补码

正数原码、反码、补码相同，都是直接将数字转化为32位二进制序列。

以int类型数据-13为例，环境以x32为准。

对于负数：

类型	含义	13对应的序列
原码	直接将数字转化为二进制序列	10000000000000000000000000001101
反码	原码除符号位外，其余按位取反	11111111111111111111111111110010
补码	反码+1	11111111111111111111111111110011

而补码也可以不通过逆向方法得到原码，而是先取反，后==+1==。

1.2、大、小端

1.2.1、引子

#include<stdio.h>int main()
{int a = 0x11223344;return 0;
}

在内存窗口看看&a:

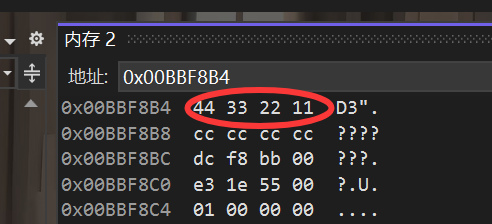
我们会发现，vs 2022中内存从低到高，排列依次为44 33 22 11。

为什么会这样，看起来是反着来的？

这个时候，就要了解大小端的概念。

1.2.2、概念

大端：数据的低位存储到内存的高地址处，数据的高位存储到内存的低地址处。
小端：数据的低位存储到内存的低地址处，数据的高位存储到内存的高地址处。

我们也可以设计一段代码，来判断当前机器是大端，还是小端：

#include<stdio.h>int sys_check()
{int a = 1;return *((char*)&a);
}int main()
{int ret = sys_check();if (1 == ret){printf("小端\n");}else{printf("大端\n");}return 0;
}

2、浮点型数据在内存中的存储方法

浮点型数据的存储方法，与整型不同。

2.1、存储的方法

根据国际标准IEEE（电气电子工程师学会）754，任意一个二进制浮点数V，可以表示成下面的形式：

$$V=(-1{)}^S\ast M\ast 2^E.$$

· S代表该数的正负，S = 0为正，S = 1为负。
· M的范围：1 <= M < 2。
· E代表数量级。

例如，-9.5，
转化为二进制：-1001.1，
用公式表达：(-1)^(1)*1.0011*2^3，
其中，S = 1 M = 1.0011 E = 3。

32位机器，从左往右，第一位符号位，后8位存E，剩余位存M。
64位机器，从左往右，第一位符号位，后11位存E，剩余位存M。

以32位的-9.5为例：

1. 负数，第32位1。

2. 第31~24位，并不是直接存储3的二进制序列，而是先3 + 127 = 130（64位，就加1023），存130，也就是说，存10000010。

3. 剩下位，去掉小数点左边1，也就是存0011，后面补19个0。

所以结果：

$$11000001000110000000000000000000$$

转化为十六进制数，为：
$$C1180000$$

是不是呢：

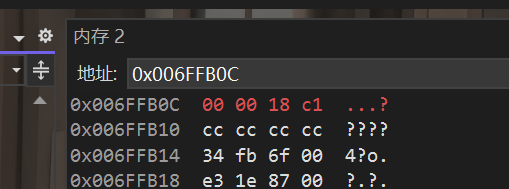
由于vs 2022为小端，所以看起来是反着来的。

2.2、取的方法

2.2.1、E不全为0，或E不全为1

就是常规方法，根据上面操作，反过来。

2.2.2、E全为0

这时，E就是1 - 127 = -126或1 - 1023 = 1022，M就不要加回1，而是0.xxxxxxxx。

这样做，是为了表示正负0，以及接近0的很小的值。

2.2.3、E全为1

此时，E就很大了，表示正负无穷。