当前位置：首页 > news >正文

【数据结构】基于Floyd算法的最短路径求解

news 2025/10/17 6:30:02

【实验目的】
1.掌握图的邻接矩阵表示法。
2.掌握求解最短路径的Floyd算法。
【实验内容】
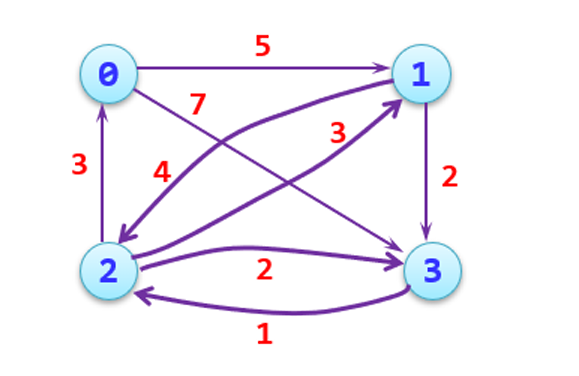
1、问题描述
一张地图包括n个城市，假设城市间有m条路径（有向图），每条路径的长度已知。利用Floyd算法求出各个城市之间的最短路径。
2、输入要求
多组数据，每组数据有m+3行。第一行为两个整数n和m，分别代表城市个数n和路径条数m。第二行有n个字符，代表每个城市的编号。第三行到第 m+2行每行有两个字符a和b和一个整数d，代表从城市a到城市b有一条距离为d的路。当n和m都等于0时，输入结束。
3、输出要求
第1行开始打印记录城市vi和vj之间的最短路径长度的二维数组，即D[i][j]。第2行开始打印最短路径上城市vj的前一城市编号的二维数组，即 Path[i][j]。

输入样例:

输出样例:

C++代码如下：

#include<iostream> 
using namespace std;
#define MaxInt 32767  //表示极大值 
#define MVNum 100  //最大顶点数 
typedef char VerTexType;   //设置顶点类型为字符型 
typedef int ArcType;    //设置权重为整型 
typedef struct
{VerTexType vexs[MVNum];    //顶点表 ArcType arcs[MVNum][MVNum];   //邻接矩阵 int vexnum, arcnum;  //顶点数和边数 
}AMGraph;
//从顶点表中查找顶点
int LocateVex(AMGraph G, VerTexType u);
//构造有向网
int CreateDN(AMGraph& G);
// 佛洛依德算法的实现
void floydWarshall(AMGraph G);
int main()
{while (1){AMGraph G;CreateDN(G);if (G.vexnum == 0 && G.arcnum == 0){break;}floydWarshall(G);}return 0;
}
//从顶点表中查找顶点
int LocateVex(AMGraph G, VerTexType u)
{int i;for (i = 0;i < G.vexnum;i++){if (u == G.vexs[i]){return i;}}return -1;
}
int CreateDN(AMGraph& G) 
{int i, j, k;cin >> G.vexnum >> G.arcnum;for (i = 0;i < G.vexnum;i++){cin >> G.vexs[i];}for (i = 0;i < G.vexnum;i++){for (j = 0;j < G.vexnum;j++){G.arcs[i][j] = MaxInt;}}for (k = 0;k < G.arcnum;k++){VerTexType v1, v2;ArcType w;cin >> v1 >> v2 >> w;i = LocateVex(G, v1);j = LocateVex(G, v2);G.arcs[i][j] = w;}return 1;
}
void floydWarshall(AMGraph G) 
{// 初始化最短路径矩阵int dist[MVNum][MVNum], i, j, k;for (i = 0; i < G.vexnum; i++){for (int j = 0; j < G.vexnum; j++){dist[i][j] = G.arcs[i][j];}}// 更新最短路径矩阵for (k = 0; k < G.vexnum; k++) {for (i = 0; i < G.vexnum; i++){for (j = 0; j < G.vexnum; j++) {if (dist[i][k] != MaxInt && dist[k][j] != MaxInt &&dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];}}}}for (i = 0;i < G.vexnum;i++){for (j = 0;j < G.vexnum;j++){if (i == j){dist[i][j] = 0;}if (dist[i][j] != MaxInt){cout << dist[i][j] << " ";}else{cout << "∞" << " ";}}cout << endl;}}

Python代码如下：

class AMGraph:def __init__(self):self.vexs = [''] * MVNum  # 顶点表，存储顶点字符self.arcs = [[MaxInt for _ in range(MVNum)] for _ in range(MVNum)]  # 邻接矩阵，存储边权self.vexnum = 0  # 实际顶点数量self.arcnum = 0  # 实际边数量MaxInt = 32767  # 表示极大值（不可达）
MVNum = 100     # 最大顶点数# 从顶点表中查找顶点对应的索引，未找到返回-1
def LocateVex(G, u):for i in range(G.vexnum):if G.vexs[i] == u:return ireturn -1# 构造有向网（读取输入初始化图结构，适配“一行内空格分隔”的输入格式）
def CreateDN(G):# 读取顶点数和边数vexnum, arcnum = map(int, input().split())G.vexnum = vexnumG.arcnum = arcnumif G.vexnum == 0 and G.arcnum == 0:return 0  # 输入“0 0”时退出循环# 读取一行内的所有顶点（空格分隔，如“0 1 2 3”）vertices = input().split()for i in range(G.vexnum):G.vexs[i] = vertices[i]# 初始化邻接矩阵为“极大值”（表示初始不可达）for i in range(G.vexnum):for j in range(G.vexnum):G.arcs[i][j] = MaxInt# 读取每条边的信息（一行内空格分隔，如“0 1 5”）for k in range(G.arcnum):v1, v2, w = input().split()w = int(w)i = LocateVex(G, v1)j = LocateVex(G, v2)G.arcs[i][j] = wreturn 1# Floyd-Warshall算法：求解所有顶点对之间的最短路径
def floydWarshall(G):# 初始化距离矩阵（复制邻接矩阵的初始值）dist = [[0 for _ in range(G.vexnum)] for _ in range(G.vexnum)]for i in range(G.vexnum):for j in range(G.vexnum):dist[i][j] = G.arcs[i][j]# 核心：通过中间顶点k，更新所有顶点对的最短路径for k in range(G.vexnum):for i in range(G.vexnum):for j in range(G.vexnum):# 若i→k和k→j都可达，且经过k的路径更短，则更新if dist[i][k] != MaxInt and dist[k][j] != MaxInt and dist[i][k] + dist[k][j] < dist[i][j]:dist[i][j] = dist[i][k] + dist[k][j]# 输出结果（处理自身到自身、不可达的情况）for i in range(G.vexnum):row = []for j in range(G.vexnum):if i == j:val = 0elif dist[i][j] != MaxInt:val = dist[i][j]else:val = "∞"  # 不可达用∞表示row.append(str(val))print(" ".join(row))def main():while True:G = AMGraph()if CreateDN(G) == 0:  # 输入“0 0”时退出循环breakfloydWarshall(G)if __name__ == "__main__":main()

Java代码如下：

import java.util.Scanner;public class FloydWarshall {static final int MaxInt = 32767; // 表示极大值（不可达）static final int MVNum = 100;    // 最大顶点数// 图的结构类，对应C++的AMGraph结构体static class AMGraph {char[] vexs = new char[MVNum];    // 顶点表，存储顶点字符int[][] arcs = new int[MVNum][MVNum]; // 邻接矩阵，存储边的权值int vexnum, arcnum;  // 实际顶点数和边数}// 从顶点表中查找顶点对应的索引，未找到返回-1static int LocateVex(AMGraph G, char u) {for (int i = 0; i < G.vexnum; i++) {if (G.vexs[i] == u) {return i;}}return -1;}// 构造有向网（读取输入初始化图，适配“一行内空格分隔”的输入格式）static int CreateDN(AMGraph G, Scanner scanner) {G.vexnum = scanner.nextInt();G.arcnum = scanner.nextInt();scanner.nextLine(); // 消耗当前行的剩余换行符，避免影响后续整行读取if (G.vexnum == 0 && G.arcnum == 0) {return 0; // 输入“0 0”时退出循环}// 读取一行内的所有顶点（空格分隔，如“A B C”）String[] vertices = scanner.nextLine().split(" ");for (int i = 0; i < G.vexnum; i++) {G.vexs[i] = vertices[i].charAt(0);}// 初始化邻接矩阵为“极大值”（表示初始不可达）for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {G.arcs[i][j] = MaxInt;}}// 读取每条边的信息（一行内空格分隔，如“A B 5”）for (int k = 0; k < G.arcnum; k++) {String[] edgeParts = scanner.nextLine().split(" ");char v1 = edgeParts[0].charAt(0);char v2 = edgeParts[1].charAt(0);int w = Integer.parseInt(edgeParts[2]);int i = LocateVex(G, v1);int j = LocateVex(G, v2);G.arcs[i][j] = w;}return 1;}// Floyd-Warshall算法：求解所有顶点对之间的最短路径static void floydWarshall(AMGraph G) {// 初始化距离矩阵（复制邻接矩阵的初始值）int[][] dist = new int[G.vexnum][G.vexnum];for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {dist[i][j] = G.arcs[i][j];}}// 核心逻辑：通过中间顶点k，更新所有顶点对的最短路径for (int k = 0; k < G.vexnum; k++) {for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {// 若i→k和k→j都可达，且经过k的路径更短，则更新i→j的距离if (dist[i][k] != MaxInt && dist[k][j] != MaxInt && dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];}}}}// 输出结果（处理“自身到自身”和“不可达”的情况）for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {if (i == j) {System.out.print("0 ");} else if (dist[i][j] != MaxInt) {System.out.print(dist[i][j] + " ");} else {System.out.print("∞ ");}}System.out.println();}}public static void main(String[] args) {Scanner scanner = new Scanner(System.in);while (true) {AMGraph G = new AMGraph();if (CreateDN(G, scanner) == 0) { // 输入“0 0”时退出循环break;}floydWarshall(G);}scanner.close();}
}