基于目标信息最大化的高分辨率雷达波形设计——论文阅读

基于目标信息最大化的高分辨率雷达波形设计

H. Xu, J. Zhang, W. Liu, S. Wang and C. Li, “High-Resolution Radar Waveform Design Based on Target Information Maximization,” in IEEE Transactions on Aerospace and Electronic Systems, vol. 56, no. 5, pp. 3577-3587, Oct. 2020, doi: 10.1109/TAES.2020.2976085.

1. 引言

雷达设计的核心目标是最大化目标信息的获取，从而实现高精度的检测、分类和最终识别。得益于高分辨率成像雷达，如合成孔径雷达（SAR），即使是微小、紧密间隔的目标也变得可见和可识别。发射的雷达波形决定了距离分辨率，可以将其视为雷达获取信息的信道。因此，如何设计更好的波形以最大化从目标获取的信息并同时获得高分辨率具有重要意义。

线性调频波形（LFMW）作为成像雷达中广泛使用的经典波形之一，在点目标的信噪比（SNR）最大化准则下是最优的，但对于扩展目标或空间分布目标，它并不表现出优越的信息获取能力。早在1964年，Woodward就指出盲目追求SNR可能会误导雷达设计和数据处理，因为没有理论表明最大化SNR可以确保最大信息获取。Bell也提出了类似的观点。因此，开发基于最大化目标信息准则（MTIC）的高分辨率波形设计方法将是重要且有益的。

2. 雷达信息获取模型

雷达信息获取过程可以用图1所示的无记忆信道模型来描述。目标散射特性函数$G(t)$是决定信息源的随机过程，它与波形函数$x(t)$相互作用进行空间传输。调制信号$Z(t)$随后被加性噪声$N(t)$破坏，通过理想带通滤波器$b_f(t)$形成接收信号$Y(t)$：

$$Y(t)=[G(t)\otimes x(t)+N(t)]\otimes b_f(t)$$

其中$\otimes$表示线性卷积算子。小写字母和大写字母分别用于表示确定性信号和随机过程。

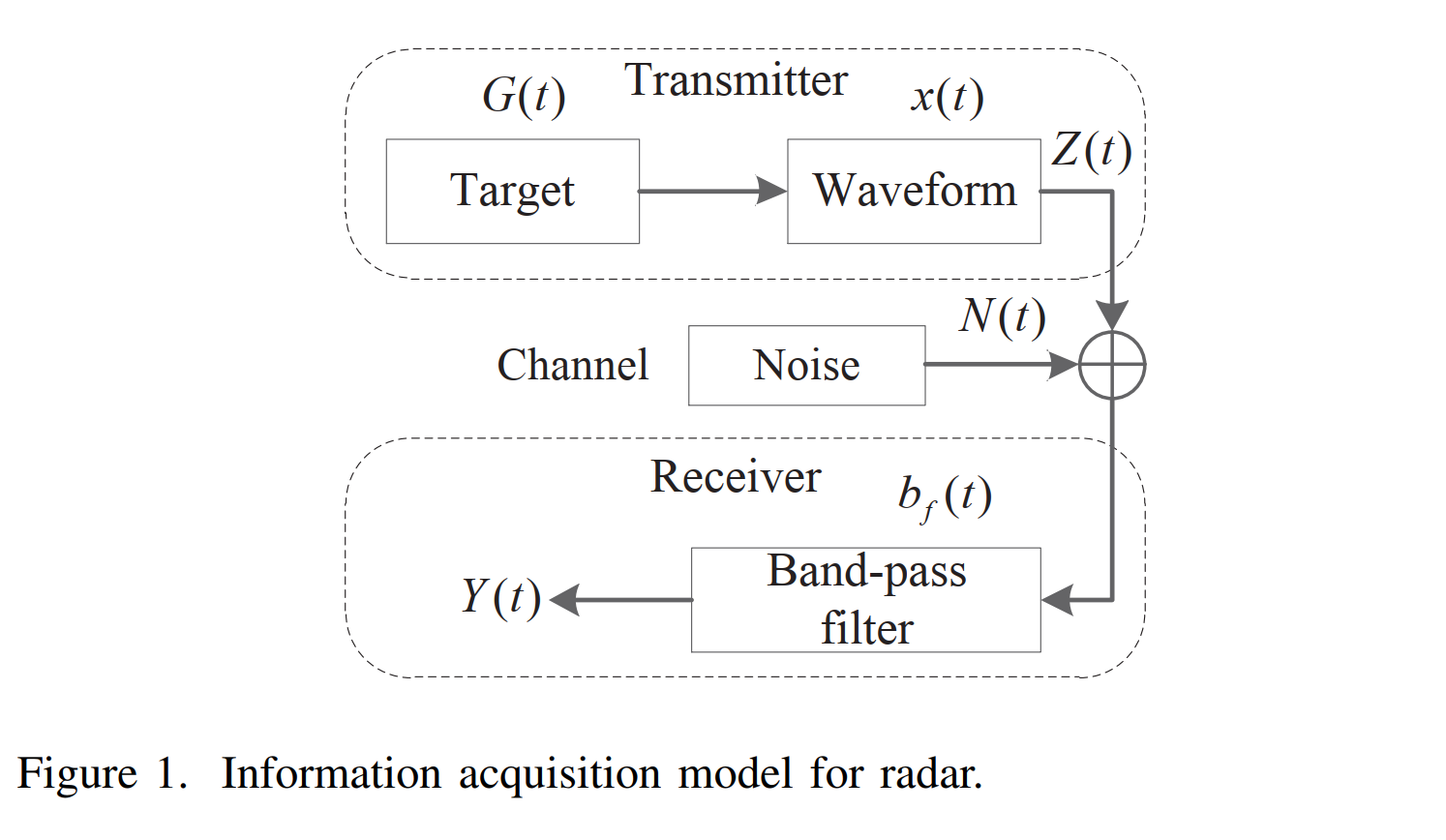
图1描述：信息获取模型框图显示了雷达系统的基本组成。左侧是发射机产生波形$x(t)$，中间是包含目标$G(t)$的信道和噪声$N(t)$，右侧是接收机通过带通滤波器$b_f(t)$处理得到输出信号$Y(t)$。

基于信息论，$G(t)$和$Y(t)$之间的互信息$I[Y(t);G(t)]$表示雷达从观测信号$Y(t)$中可以获得多少目标信息。因此，MTIC就是要最大化$I[Y(t);G(t)]$，目标函数建立为：

max⁡{I[Y(t);G(t)]}\max \{I[Y(t); G(t)]\}max{I[Y(t);G(t)]}

由于$x(t)$是确定性信号，max⁡{I[Y(t);G(t)]}\max\{I[Y(t); G(t)]\}max{I[Y(t);G(t)]}等价于max⁡{I[Y(t);Z(t)]}\max\{I[Y(t); Z(t)]\}max{I[Y(t);Z(t)]}。然而，找到max⁡{I[Y(t);Z(t)]}\max\{I[Y(t); Z(t)]\}max{I[Y(t);Z(t)]}的解是一个众所周知的困难任务，在大多数现实情况下是不可行的。因此，有必要将目标函数转换为等价的新形式。

在许多工程优化的实际问题中，最大化皮尔逊相关系数（PCC）$|{\rho }_{Y(t)Z(t)}|$是最大化互信息的一种方法，无论这些随机变量遵循何种分布：

max⁡{∣ρY(t)Z(t)∣}⇒max⁡{I[Y(t);Z(t)]}\max\{|\rho_{Y(t)Z(t)}|\} \Rightarrow \max\{I[Y(t);Z(t)]\}max{∣ρY(t)Z(t)​∣}⇒max{I[Y(t);Z(t)]}

因此，本文引入PCC来表示MTIC下的波形设计目标函数，相应的约束优化问题写为：

max⁡x(t){∣ρY(t)Z(t)∣}s.t.x(t)∈D\max_{x(t)} \{|\rho_{Y(t)Z(t)}|\} \quad \text{s.t.} \quad x(t) \in \mathcal{D}x(t)max​{∣ρY(t)Z(t)​∣}s.t.x(t)∈D

其中$\mathcal{D}$表示$x(t)$的约束集或可行集。由于雷达波形在大多数实际应用中必须限制能量或功率并提供高分辨率，因此恒功率和高分辨率约束被包含在集合$\mathcal{D}$中。

3. 恒功率约束下的最优波形推导

3.1 离散信号模型

连续时间信号的离散时间处理在带限系统中很常见。直接设计离散雷达波形可以避免与模拟波形相比在接收机信号处理中由模数转换引起的近似问题。因此，我们直接以信号模型的离散时间形式呈现波形设计。

考虑信号的离散版本，其中$\mathbf{g}\in {\mathbb{C}}^{l\times 1}$、$\mathbf{x}\in {\mathbb{C}}^{n\times 1}$、${\mathbf{n}}^{\prime }\in {\mathbb{C}}^{m\times 1}$、$\mathbf{n}\in {\mathbb{C}}^{m\times 1}$和$\mathbf{y}\in {\mathbb{C}}^{m\times 1}$分别表示离散化的目标散射、波形、加性噪声、带通滤波后的加性噪声和接收信号。对应于连续模型，离散信号模型可以表示为：

$$\mathbf{y}=[\mathbf{g}\otimes \mathbf{x}+{\mathbf{n}}^{\prime }]\otimes \mathbf{b}=\mathbf{g}\otimes \mathbf{x}+\mathbf{n}=\mathbf{z}+\mathbf{n}$$

线性卷积算子可以通过Toeplitz矩阵实现，定义为：

$$\mathbf{G}=\left[\begin{array}{ccccc}g(0)& 0& \cdots & \cdots & 0\\ g(1)& g(0)& \ddots & \cdots & 0\\ ⋮& ⋮& \ddots & \ddots & ⋮\\ g(l-1)& g(l-2)& \cdots & g(0)& 0\\ 0& g(l-1)& g(l-2)& \cdots & g(0)\\ ⋮& 0& g(l-1)& \cdots & g(1)\\ ⋮& ⋮& 0& \ddots & ⋮\\ 0& 0& \cdots & 0& g(l-1)\end{array}\right]$$

其中$\mathbf{G}\in {\mathbb{C}}^{m\times n}$是$\mathbf{g}$的Toeplitz矩阵。这样，离散模型变为：

$$\mathbf{y}=\mathbf{Gx}+\mathbf{n}=\mathbf{z}+\mathbf{n}$$

3.2 皮尔逊相关系数推导

设$m_y$和$m_z$分别表示$\mathbf{y}$和$\mathbf{z}$的均值，$E[\cdot ]$表示期望操作。假设噪声零均值且与目标相关的信号独立，因此$m_y=m_z$。$\mathbf{y}$和$\mathbf{z}$的PCC可以推导为：

$${\rho }_{YZ}=\frac{E[(\mathbf{y}-m_y{)}^H(\mathbf{z}-m_z)]}{\sqrt{E[(\mathbf{y}-m_y{)}^H(\mathbf{y}-m_y)]E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]}}$$

$$=\frac{\sqrt{{\mathbf{x}}^{H}E[{\mathbf{G}}^H\mathbf{G}]\mathbf{x}-|m_y{|}^2}}{\sqrt{{\sigma }_N^2+{\mathbf{x}}^{H}E[{\mathbf{G}}^H\mathbf{G}]\mathbf{x}-|m_y{|}^2}}$$

进一步简化为：

$$|{\rho }_{YZ}{|}^2=1-\frac{{\sigma }_N^2}{{\sigma }_N^2+{\mathbf{x}}^H{\mathbf{R}}_G\mathbf{x}}$$

其中${\sigma }_N^2=E[{\mathbf{n}}^H\mathbf{n}]$，${\mathbf{R}}_G=E[{\mathbf{G}}^H\mathbf{G}]-[E(\mathbf{G}){]}^{H}E(\mathbf{G})$定义为目标特征矩阵。如果同时对目标函数施加恒功率和高分辨率约束，约束优化问题将变得相当复杂。因此我们首先考虑恒功率约束，并给出放松版本：

max⁡x{xHRGx}s.t.xHx=1\max_{\mathbf{x}} \{\mathbf{x}^H\mathbf{R}_G\mathbf{x}\} \quad \text{s.t.} \quad \mathbf{x}^H\mathbf{x} = 1xmax​{xHRG​x}s.t.xHx=1

这可以视为特征向量问题，恒功率约束下的最优波形${\mathbf{x}}_{opt}$是${\mathbf{R}}_G$最大特征值对应的特征向量：

$${\mathbf{x}}_{opt}={\text{eig}}_{\max (\lambda )}({\mathbf{R}}_G)$$

4. 高分辨率波形设计

4.1 最优波形的带宽分析

${\mathbf{R}}_G$的特征向量${\mathbf{u}}_0,{\mathbf{u}}_1,\cdots ,{\mathbf{u}}_{n-1}$可以视为空间${\mathbb{C}}^n$的基向量，相应的特征值是实值且按降序排列：${\lambda }_0\ge {\lambda }_1\ge \cdots \ge {\lambda }_{n-1}\ge 0$。由于${\mathbf{R}}_G$是半正定Hermitian矩阵，可以进行特征分解：

$${\mathbf{R}}_G=\sum _{i=0}^{n-1}{\lambda }_i{\mathbf{u}}_i{\mathbf{u}}_i^H=\sum _{i=0}^d{\lambda }_i{\mathbf{u}}_i{\mathbf{u}}_i^H+\sum _{i=d+1}^{n-1}{\lambda }_i{\mathbf{u}}_i{\mathbf{u}}_i^H$$

对于一个小的正数${\delta }_1$，我们可以找到一个$d$，使得：

$${\Vert {\mathbf{R}}_G-\sum _{i=0}^d{\lambda }_i{\mathbf{u}}_i{\mathbf{u}}_i^H\Vert }_F^2\le {\delta }_1$$

其中$\Vert \cdot {\Vert }_F$表示Frobenius范数。

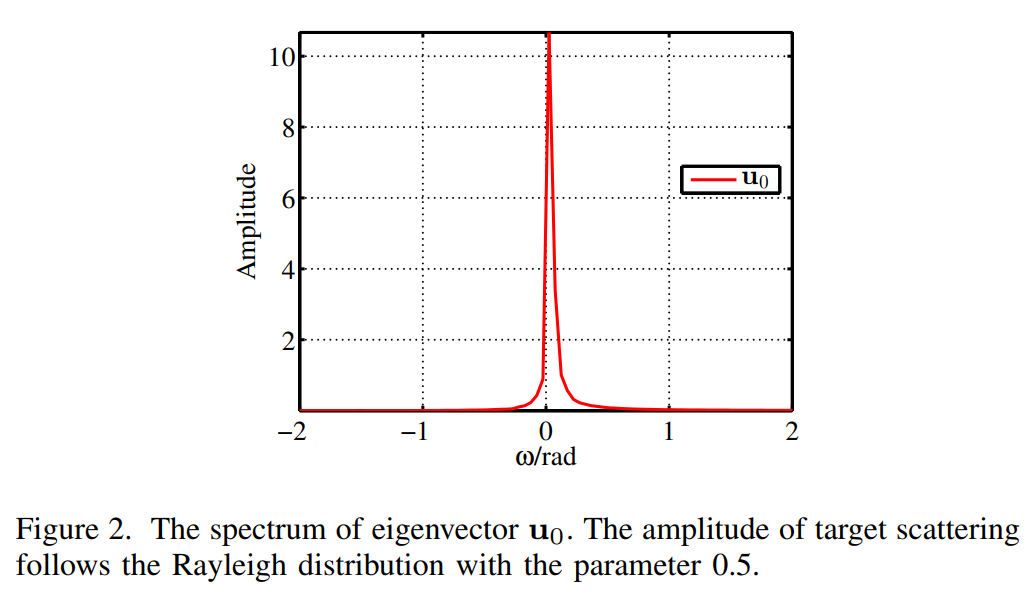
图2描述：特征向量${\mathbf{u}}_0$的频谱图。横轴为频率（rad），纵轴为幅度。图中显示了一个非常窄的主瓣，3dB带宽仅为0.0212rad，说明单个特征向量只能覆盖总频谱的一小部分。目标散射幅度服从参数为0.5的瑞利分布。

对${\mathbf{R}}_G$的列向应用离散傅里叶变换（DFT），通过分析可以发现，对应于大特征值的特征向量在低频傅里叶基上有强烈的响应，而在高频基上的投影系数很小。存在一个$v$（$0\le v<n-1$），对于所有$i=0,1,\cdots ,d$和$j=v,v+1,\cdots ,n-1$，有$\max |⟨{\mathbf{u}}_i,{\mathbf{w}}_j⟩|\le {\delta }_2$，其中${\delta }_2$是一个小的正数。

4.2 基于信息失真的高分辨率波形设计

为了克服最优波形${\mathbf{u}}_0$的有限带宽，采用与大特征值相关的多个特征向量的组合。虽然引入更多特征向量会增加带宽，但由于小特征值对应的特征向量的影响，信息获取将会减少。因此，这种组合需要在满足分辨率要求的同时不过多降低信息获取能力。

定义信息失真参数：

$$\Delta =\frac{{\mathbf{u}}_0^H{\mathbf{R}}_G{\mathbf{u}}_0-{\mathbf{x}}_{sopt}^H{\mathbf{R}}_G{\mathbf{x}}_{sopt}}{{\mathbf{u}}_0^H{\mathbf{R}}_G{\mathbf{u}}_0}=1-\frac{{\mathbf{x}}_{sopt}^H{\mathbf{R}}_G{\mathbf{x}}_{sopt}}{{\lambda }_0}$$

其中${\mathbf{x}}_{sopt}\in {\mathbb{C}}^{n\times 1}$表示同时满足功率和分辨率约束的次优波形。任何$n$维向量都可以投影到整个特征向量集上：

$${\mathbf{x}}_{sopt}=\sum _{i=0}^{n-1}{q}_i{\mathbf{u}}_i$$

其中$q_i\in \mathbb{C}$表示${\mathbf{u}}_i$的投影系数。将上式代入失真公式：

$${\Delta }_{sopt}=1-\frac{{\sum }_{i=0}^{n-1}{\lambda }_i|q_i{|}^2}{{\lambda }_0}$$

特征值直接用作相应特征向量的权重，即$q_i={\lambda }_i/\sqrt{{\sum }_{i=0}^{n-1}{\lambda }_i^2}$，得到次优波形：

$${\mathbf{x}}_{sopt}=\sum _{i=0}^{n-1}{q}_i{\mathbf{u}}_i=\frac{1}{\sqrt{{\sum }_{i=0}^{n-1}{\lambda }_i^2}}\sum _{j=0}^{n-1}{\lambda }_j{\mathbf{u}}_j$$

相应的失真为：

$${\Delta }_{{\mathbf{x}}_{sopt}}=1-\frac{1}{{\lambda }_0}\cdot \frac{{\sum }_{i=0}^{n-1}{\lambda }_i^2}{{\sum }_{j=0}^{n-1}{\lambda }_j^3}$$

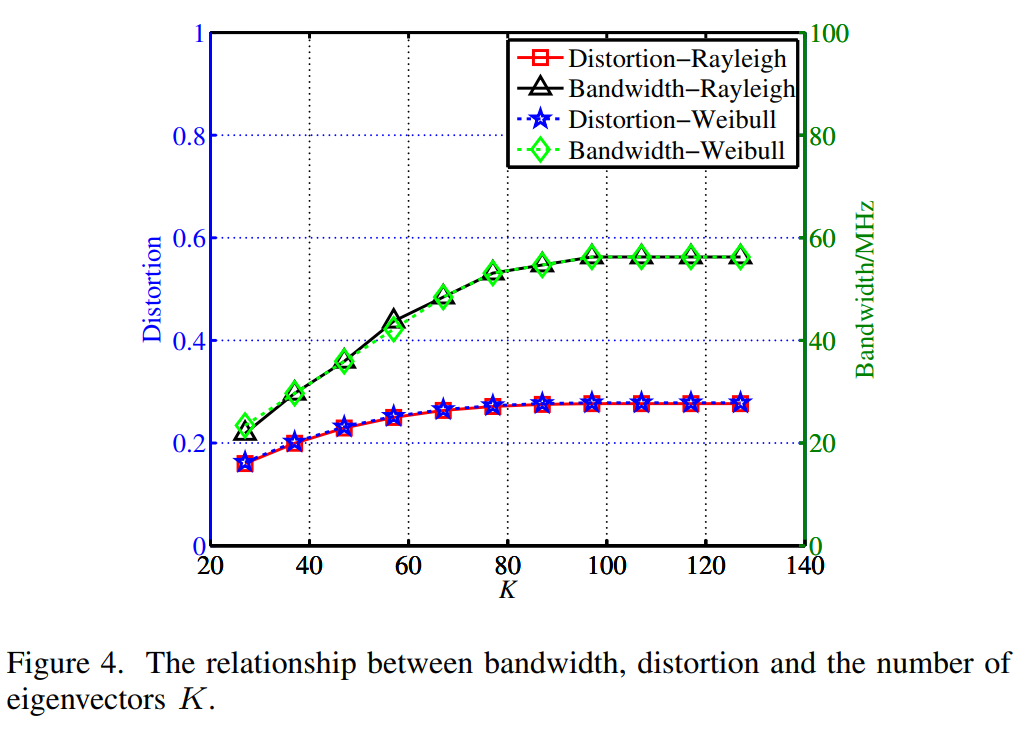
图4描述：带宽、失真与特征向量数量$K$之间的关系图。上方显示失真曲线，下方显示带宽曲线。横轴为$K$值（从20到140），左纵轴为失真（0到1），右纵轴为带宽（0到100MHz）。图中分别展示了瑞利分布和威布尔分布两种情况的结果。随着$K$增加，失真和带宽都单调增加。

通过移除几个与小特征值相关的不重要特征向量可以减少失真。令${\tilde{\mathbf{x}}}_{sopt}$表示修改后的波形：

$${\tilde{\mathbf{x}}}_{sopt}=\frac{1}{\sqrt{{\sum }_{i=0}^{K-1}{\lambda }_i^2}}\sum _{j=0}^{K-1}{\lambda }_j{\mathbf{u}}_j=\frac{1}{\sqrt{{\sum }_{i=0}^{K-1}|q_i{|}^2}}\sum _{j=0}^{K-1}{q}_j{\mathbf{u}}_j,1\le K<n-1$$

其信息失真为：

$${\Delta }_{{\tilde{\mathbf{x}}}_{sopt}}=1-\frac{1}{{\lambda }_0}\cdot \frac{{\sum }_{i=0}^{K-1}{\lambda }_i^2}{{\sum }_{j=0}^{K-1}{\lambda }_j^3}$$

5. 仿真结果与分析

5.1 理论分析验证

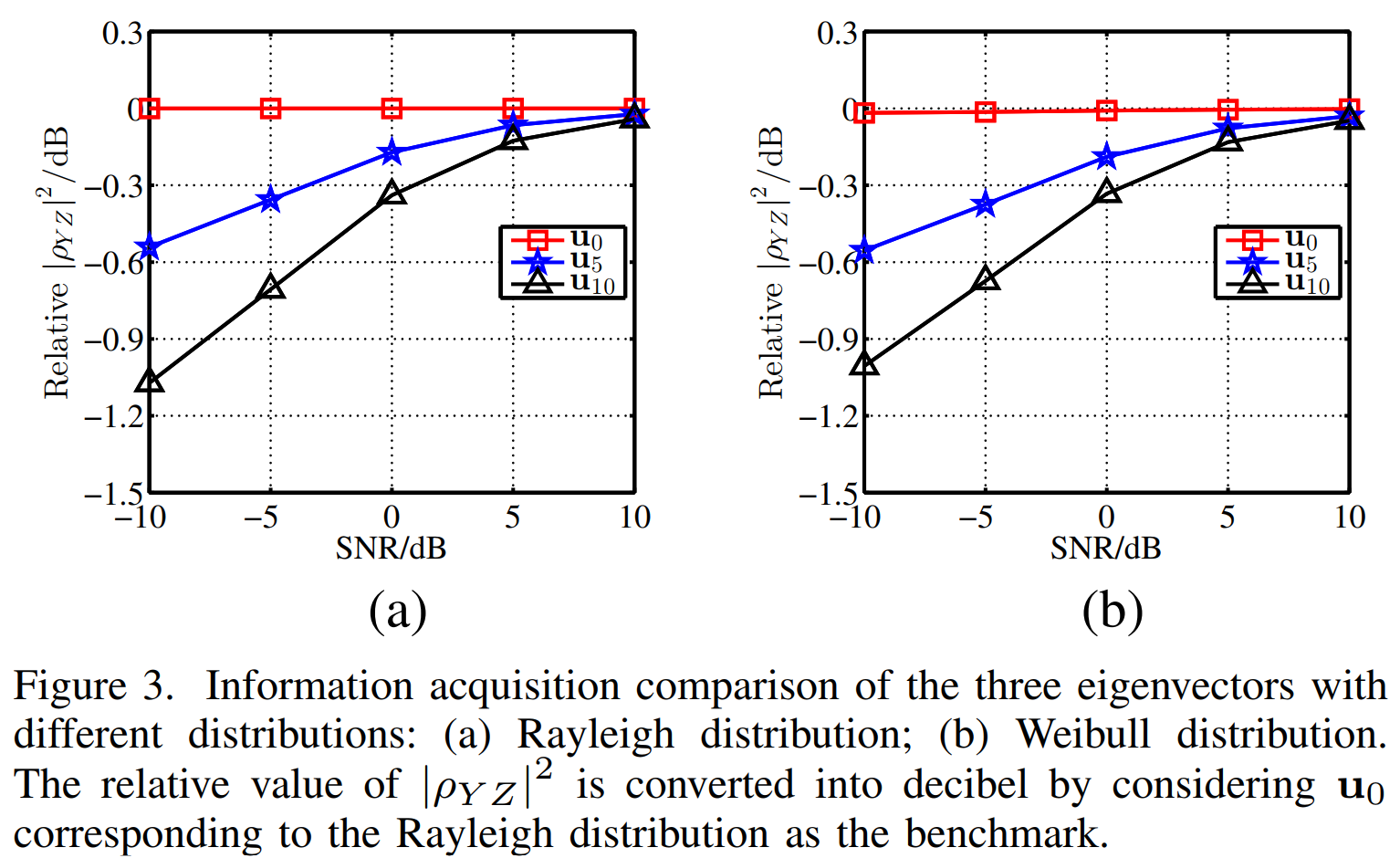
图3描述：三个特征向量的信息获取比较。(a)瑞利分布；(b)威布尔分布。横轴为SNR（dB），纵轴为相对$|{\rho }_{YZ}{|}^2$（dB）。三条曲线分别表示${\mathbf{u}}_0$、${\mathbf{u}}_5$和${\mathbf{u}}_{10}$的性能。${\mathbf{u}}_0$在所有SNR条件下都表现最佳，验证了其作为最优波形的理论分析。

5.2 性能评估

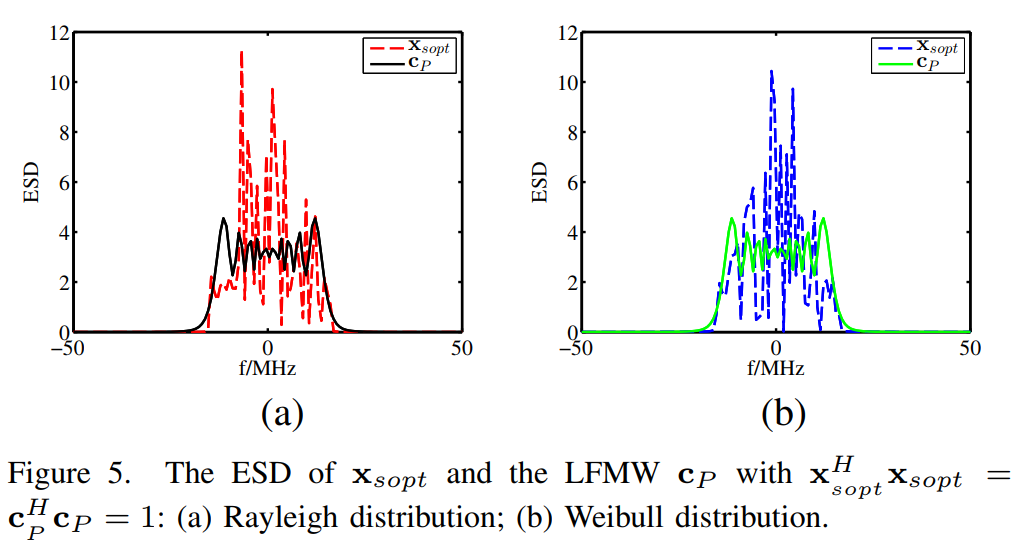
图5描述：次优波形${\mathbf{x}}_{sopt}$和LFMW的能量谱密度（ESD）比较。(a)瑞利分布；(b)威布尔分布。横轴为频率（MHz），纵轴为ESD。两种波形都满足${\mathbf{x}}_{sopt}^H{\mathbf{x}}_{sopt}={\mathbf{c}}_P^H{\mathbf{c}}_P=1$的功率归一化条件。

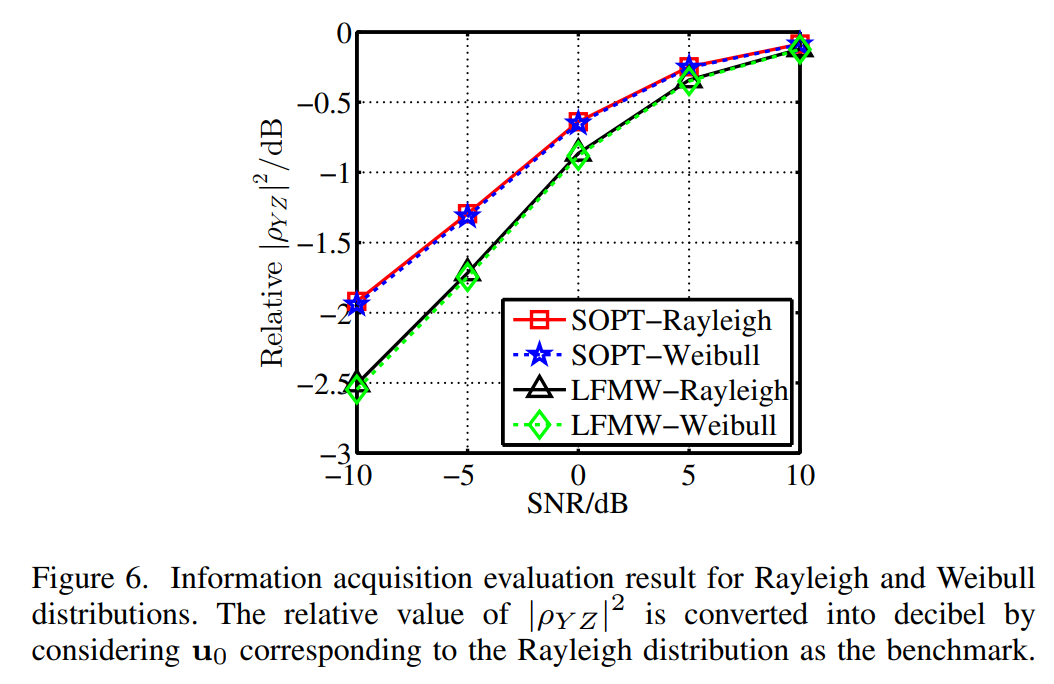
图6描述：瑞利和威布尔分布下次优波形和LFMW的信息获取评估结果。横轴为SNR（dB），纵轴为相对$|{\rho }_{YZ}{|}^2$（dB）。四条曲线分别表示SOPT-Rayleigh、SOPT-Weibull、LFMW-Rayleigh和LFMW-Weibull。次优波形在两种分布下都优于LFMW约0.6dB。

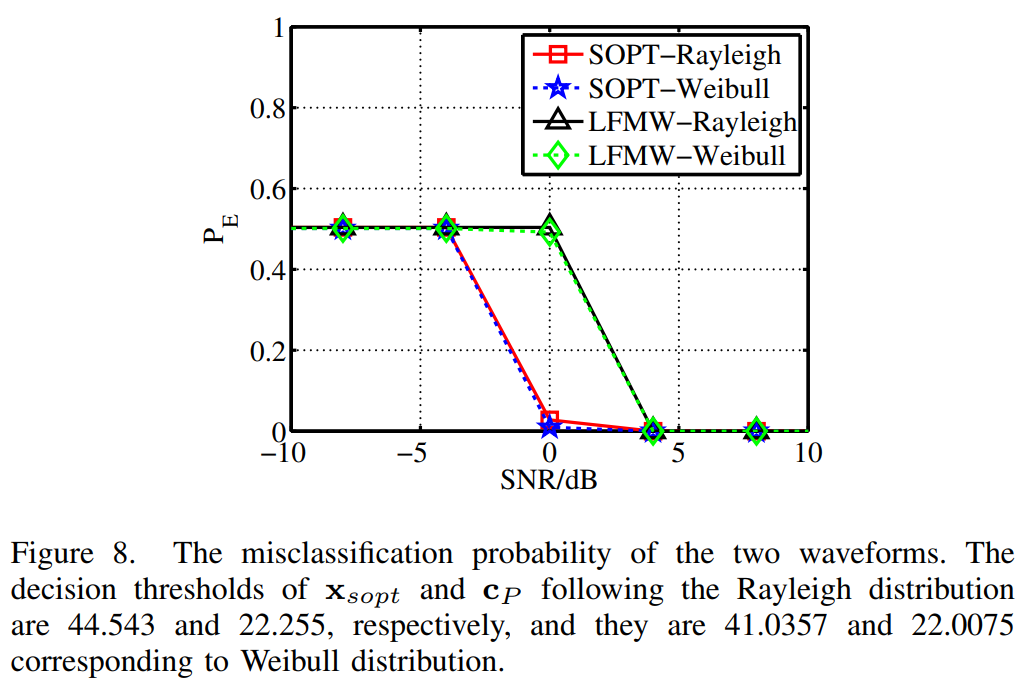
图8描述：两种波形的误分类概率。横轴为SNR（dB），纵轴为误分类概率$P_E$。结果显示次优波形的误分类概率低于LFMW，特别是在低SNR时优势明显。

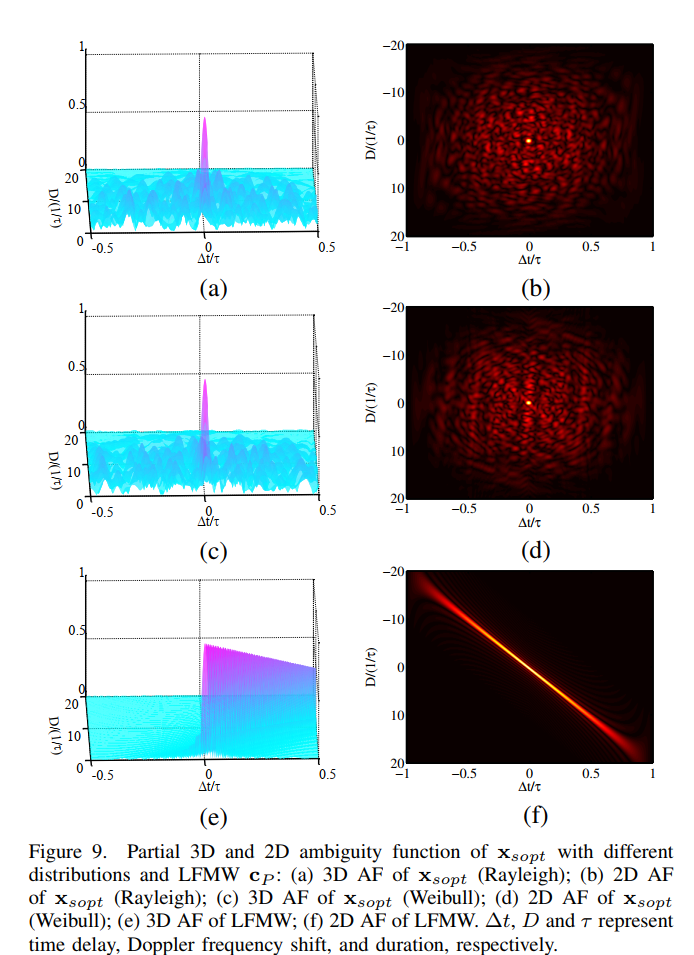
图9描述：部分3D和2D模糊函数。(a)(b)为${\mathbf{x}}_{sopt}$（瑞利）的3D和2D模糊函数；©(d)为${\mathbf{x}}_{sopt}$（威布尔）的3D和2D模糊函数；(e)(f)为LFMW的3D和2D模糊函数。${\mathbf{x}}_{sopt}$呈现针状，而LFMW呈现刀刃状。

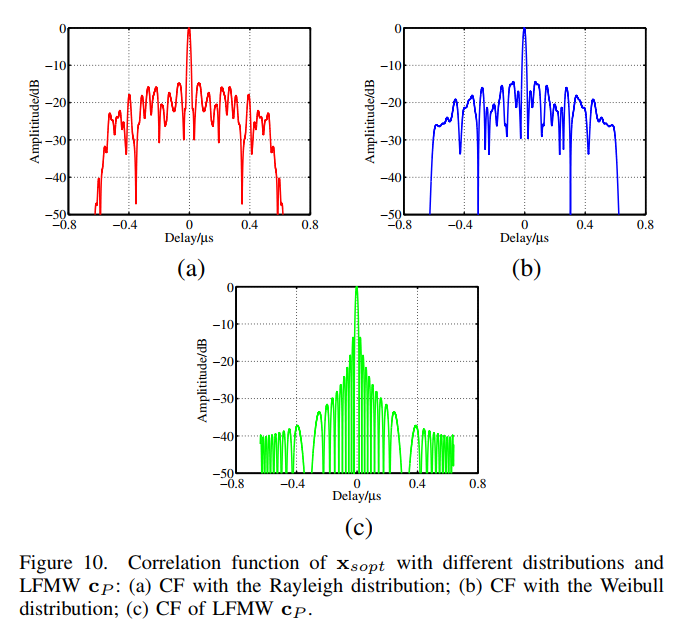
图10描述：相关函数比较。(a)瑞利分布下${\mathbf{x}}_{sopt}$的相关函数；(b)威布尔分布下${\mathbf{x}}_{sopt}$的相关函数；©LFMW的相关函数。横轴为延迟（μs），纵轴为幅度（dB）。

6. 结论

本文提出了一种基于最大化目标信息准则的高分辨率雷达波形设计新方法，该方法不对目标散射的统计分布做假设。通过最大化皮尔逊相关系数建立目标函数，设计被转换为优化问题并分两步求解。首先，在时域中推导了恒功率约束下离散波形的闭式表达式。其次，基于最优解的带宽分析，引入了考虑信息失真的分辨率改进方法，提出了在满足恒功率和分辨率要求的同时的次优波形。

性能分析表明，次优波形的分辨率略低于LFMW，但在峰值旁瓣比（PSLR）、信息获取和分类方面更加理想。仿真结果显示，在相同的功率和时间带宽积下，所设计的波形通过所提出的方法在MTIC下可以获取更高的目标信息量，并最终实现比经典LFMW更好的分类结果。基于分辨率评估指标的结果表明，次优波形也具有高分辨率。

---

附录A：皮尔逊相关系数的推导

从离散信号模型开始：
$$\mathbf{y}=\mathbf{Gx}+\mathbf{n}=\mathbf{z}+\mathbf{n}$$

计算$\mathbf{y}$和$\mathbf{z}$的皮尔逊相关系数：

$${\rho }_{YZ}=\frac{E[(\mathbf{y}-m_y{)}^H(\mathbf{z}-m_z)]}{\sqrt{E[(\mathbf{y}-m_y{)}^H(\mathbf{y}-m_y)]E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]}}$$

由于$\mathbf{y}=\mathbf{z}+\mathbf{n}$且噪声与信号独立，有：
$$E[(\mathbf{y}-m_y{)}^H(\mathbf{z}-m_z)]=E[(\mathbf{z}-m_z+\mathbf{n}{)}^H(\mathbf{z}-m_z)]$$
$$=E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]+E[{\mathbf{n}}^H(\mathbf{z}-m_z)]$$
$$=E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]$$

其中最后一步利用了噪声与信号独立的假设。

对于分母的第一项：
$$E[(\mathbf{y}-m_y{)}^H(\mathbf{y}-m_y)]=E[(\mathbf{z}-m_z+\mathbf{n}{)}^H(\mathbf{z}-m_z+\mathbf{n})]$$
$$=E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]+E[{\mathbf{n}}^H\mathbf{n}]$$
$$=E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]+{\sigma }_N^2$$

因此：
$${\rho }_{YZ}=\frac{E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]}{\sqrt{(E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]+{\sigma }_N^2)\cdot E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]}}$$

令${\sigma }_z^2=E[(\mathbf{z}-m_z{)}^H(\mathbf{z}-m_z)]$，则：
$${\rho }_{YZ}=\frac{{\sigma }_z^2}{\sqrt{({\sigma }_z^2+{\sigma }_N^2)\cdot {\sigma }_z^2}}=\frac{{\sigma }_z}{\sqrt{{\sigma }_z^2+{\sigma }_N^2}}$$

因此：
$$|{\rho }_{YZ}{|}^2=\frac{{\sigma }_z^2}{{\sigma }_z^2+{\sigma }_N^2}=1-\frac{{\sigma }_N^2}{{\sigma }_z^2+{\sigma }_N^2}$$

由于$\mathbf{z}=\mathbf{Gx}$，有：
$${\sigma }_z^2=E[(\mathbf{Gx}-m_z{)}^H(\mathbf{Gx}-m_z)]$$

当$E[\mathbf{G}]=0$时（零均值目标），$m_z=0$，因此：
$${\sigma }_z^2=E[{\mathbf{x}}^H{\mathbf{G}}^H\mathbf{Gx}]={\mathbf{x}}^{H}E[{\mathbf{G}}^H\mathbf{G}]\mathbf{x}={\mathbf{x}}^H{\mathbf{R}}_G\mathbf{x}$$

最终得到：
$$|{\rho }_{YZ}{|}^2=1-\frac{{\sigma }_N^2}{{\sigma }_N^2+{\mathbf{x}}^H{\mathbf{R}}_G\mathbf{x}}$$

附录B：失真减少的证明

比较${\Delta }_{{\mathbf{x}}_{sopt}}$和${\Delta }_{{\tilde{\mathbf{x}}}_{sopt}}$的差：

$${\Delta }_{{\mathbf{x}}_{sopt}}-{\Delta }_{{\tilde{\mathbf{x}}}_{sopt}}=\frac{1}{{\lambda }_0}\sum _{i=0}^{K-1}|q_i{|}^2\sum _{j=0}^{K-1}{\lambda }_j|q_j{|}^2-\frac{1}{{\lambda }_0}\sum _{i=0}^{n-1}{\lambda }_i|q_i{|}^2$$

由于${\lambda }_0\ge {\lambda }_1\ge \cdots \ge {\lambda }_{n-1}\ge 0$，我们有：

$${\lambda }_0({\Delta }_{{\mathbf{x}}_{sopt}}-{\Delta }_{{\tilde{\mathbf{x}}}_{sopt}})\ge \sum _{i=0}^{K-1}|q_i{|}^2\sum _{j=0}^{K-1}{\lambda }_j|q_j{|}^2-\left(\sum _{i=0}^{K-1}{\lambda }_i|q_i{|}^2+{\lambda }_K\sum _{i=K}^{n-1}|q_i{|}^2\right)$$

展开并重新排列：

$$=\sum _{j=0}^{K-1}{\lambda }_j\left(\frac{|q_j{|}^2}{{\sum }_{i=0}^{K-1}|q_i{|}^2}-|q_j{|}^2\right)-{\lambda }_K\left(1-\sum _{j=0}^{K-1}|q_j{|}^2\right)$$

由于${\sum }_{i=0}^{K-1}|q_i{|}^2\le 1$，上式变为：

$$\ge {\lambda }_K\left(\frac{{\sum }_{j=0}^{K-1}|q_j{|}^2}{{\sum }_{i=0}^{K-1}|q_i{|}^2}-\sum _{j=0}^{K-1}|q_j{|}^2\right)-{\lambda }_K\left(1-\sum _{j=0}^{K-1}|q_j{|}^2\right)=0$$

因此：
$${\Delta }_{{\mathbf{x}}_{sopt}}-{\Delta }_{{\tilde{\mathbf{x}}}_{sopt}}\ge 0$$

这证明了失真随着$K$的减小而减小。

附录C：特征向量频谱分析

对目标特征矩阵${\mathbf{R}}_G$的列向应用DFT：

$${\mathbf{W}}^H{\mathbf{R}}_G={\mathbf{W}}^H\sum _{i=0}^d{\lambda }_i{\mathbf{u}}_i{\mathbf{u}}_i^H+{\mathbf{W}}^{H}e({\delta }_1)$$

其中$\mathbf{W}$是DFT矩阵：

$$\mathbf{W}=[{\mathbf{w}}_0,{\mathbf{w}}_1,\cdots ,{\mathbf{w}}_{n-1}]$$
$$=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ 1& w^1& \cdots & w^{n-1}\\ ⋮& ⋮& \ddots & ⋮\\ 1& w^{n-1}& \cdots & w^{(n-1{)}^2}\end{array}\right]$$

其中$w=e^{j2\pi /n}$。

展开得：

$${\mathbf{W}}^H{\mathbf{R}}_G=\sum _{i=0}^d{\lambda }_i\left[\begin{array}{c}⟨{\mathbf{u}}_i,{\mathbf{w}}_0⟩\\ ⟨{\mathbf{u}}_i,{\mathbf{w}}_1⟩\\ ⋮\\ ⟨{\mathbf{u}}_i,{\mathbf{w}}_{n-1}⟩\end{array}\right]{\mathbf{u}}_i^H+{\mathbf{W}}^{H}e({\delta }_1)$$

由于${\mathbf{R}}_G$可以视为与目标散射频谱相关的二维基带信号，对应于大特征值的特征向量${\mathbf{u}}_i$（$i=0,1,\cdots ,d$）对低频傅里叶基有强烈响应，对高频基的投影系数很小。这解释了为什么最优波形${\mathbf{u}}_0$的带宽有限。