大模型前世今生（十四）：保持训练稳定性

Hessian 矩阵是观察性的，而非指令性的。它不控制或调整优化过程，它告诉你损失函数是如何围绕当前权重形成的，但不会主动干预。

所以，假设 Hessian 矩阵显示“哦，这部分损失函数非常陡峭，或者曲率是负的”，会发生什么？

1. 标准梯度下降无法明确地识别它

梯度下降只使用一阶导数（梯度），它只是沿着感觉上的坡度向下移动一步。如果坡度非常陡峭（Hessian 矩阵的特征值很大），则步骤可能会超出预期。如果斜率平坦（特征值较小），则进展缓慢。

梯度下降会持续进行，忽略 Hessian 矩阵；Hessian 矩阵仅用于诊断地形。

2. 高级优化器会隐式地使用 Hessian 矩阵信息

某些优化器（例如牛顿法）会考虑 Hessian 矩阵，逆 Hessian 矩阵会沿曲率方向重新调整梯度。在陡峭方向上，步长较小；在平坦方向上，步长较大。

 

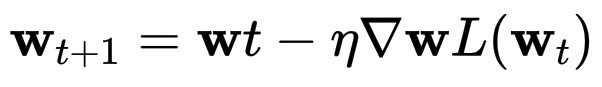
\mathbf{w}_{t+1} = \mathbf{w}t - H^{-1} \nabla{\mathbf{w}} L(\mathbf{w}_t)

但在像 Transformer 这样的大型模型中，计算完整的 Hessian 矩阵是不可能的，因为有数十亿个参数。因此，我们依赖一阶方法（Adam、SGD），并让随机噪声加上学习率策略自然地引导权重趋向平坦稳定的盆地。

3. 如果训练遇到困难该怎么办？

如果梯度下降步长表现不佳（损失停滞或发散），从业者可以采取间接干预措施，如：降低学习率（在陡峭方向上减小步长），应用梯度裁剪（避免在曲率较大的方向上出现过冲），添加正则化或归一化（平滑地形），更改批量大小（修改随机噪声，有助于避开尖锐的最小值）…

Hessian 矩阵会告诉你损失可能不稳定的原因，但“修复它”始终是通过调整优化器或训练设置来完成的，而不是 Hessian 矩阵本身。所以，Hessian 就像一面地形的镜子：它不会移动徒步者，但它能告诉你地面是滑的、陡的还是宽的。我们调整的是训练步伐来影响地形本身。