Lora原理介绍
Lora(Low-Rank Adaptation),低秩适应,是一种高效微调技术通过引入可训练的低秩矩阵来修改预训练大模型的部分参数,从而在保持模型核心能力的同时适配特定任务。
预训练模型中存在一个极小的内在维度(核心);在继续训练的过程中,权重的更新依然也有这种特点,也存在一个内在维度。
权重更新:
因此可以通过矩阵分解的方式,将原本要更新的大的矩阵变为两个小的矩阵。
权重更新:; 具体做法就是在矩阵计算中增加一个旁系分支,旁系分支由两个低秩矩阵A和B组成。
训练时,输入分别与原始权重和两个低秩矩阵进行运算,共同得到最终结果,优化仅优化A和B。
训练完成后,可以将两个低秩矩阵与原始模型中的权重进行合并,合并后的模型与原始模型无异,避免了推理期间Prompt系列方法带来的额外计算量。
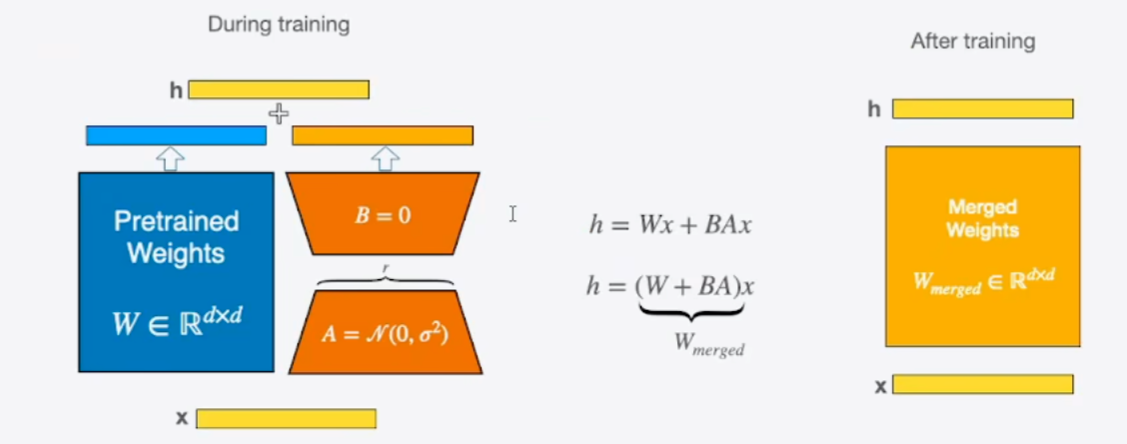
LoRA 的核心原理:用 “低秩矩阵” 替代 “全量权重更新”
预训练模型(如 Transformer)的核心是大量的权重矩阵(例如注意力层的W_q/W_k/W_v,前馈网络的线性层权重等)。全量微调时,我们会更新这些权重矩阵的所有参数,但这会导致:
- 参数数量爆炸(比如 100 亿参数的模型,全量微调需更新所有 100 亿参数);
- 训练成本高(显存、计算资源需求大);
- 过拟合风险(小数据集上容易记住噪声)。
LoRA 的解决思路是:不直接更新原权重矩阵,而是为其添加一个 “低秩扰动矩阵”,只训练这个扰动矩阵。具体来说:
-
低秩分解的本质对于模型中的一个预训练权重矩阵
W(形状为d×d,d是隐藏层维度),LoRA 假设 “任务相关的权重更新” 可以用两个低秩矩阵的乘积来表示:ΔW = A × B其中:A是随机初始化的矩阵(形状d×r),B是初始化为 0 的矩阵(形状r×d),r是 “秩”(远小于d,通常取 8、16、32),称为 “低秩维度”。
由于
r很小(比如d=4096,r=16),A和B的总参数是d×r + r×d = 2×d×r,远小于原矩阵的d×d参数(例如4096×4096≈1600万vs2×4096×16≈131072,参数减少 99% 以上)。 -
训练时的前向传播训练时,原权重矩阵
W被冻结(不更新),只训练A和B。模型的实际输出由两部分叠加而成:输出 = W × x + (A × B) × x其中x是输入向量。这样,模型既保留了预训练的知识(W × x),又能通过A×B学习任务相关的调整((A×B)×x)。 -
推理时的权重合并训练完成后,将
A×B的结果加到原权重矩阵W中:W_new = W + A × B此时,LoRA 的扰动被 “合并” 到原权重中,推理时模型结构与原始预训练模型完全一致,不会增加额外的推理延迟(这是 LoRA 相比其他参数高效方法的重要优势)。
LoRA 的优势
- 参数效率极高:仅训练低秩矩阵
A和B,参数数量通常是原模型的 0.1%~1%,大幅降低显存和计算需求。 - 效果接近全量微调:在多数任务上(尤其是大模型),LoRA 的性能可媲美全量微调,甚至在小数据集上更稳定(不易过拟合)。
- 不影响推理速度:训练后合并权重,推理时无需额外计算低秩矩阵,与原模型速度相同。
- 支持多任务切换:不同任务的
A和B可以单独保存,切换任务时只需加载对应任务的低秩矩阵,无需重新加载整个模型。
