当前位置：首页 > news >正文

解决拓扑排序

news 2025/10/15 10:47:52

拓扑排序简介

拓扑排序（Topological Sorting）是对有向无环图（DAG, Directed Acyclic Graph）顶点的一种排序方式，核心是让图中任意一条有向边对应的 “前驱顶点” 始终排在 “后继顶点” 之前，最终得到一个满足所有边的方向约束的顶点序列。它不是唯一的 —— 一个 DAG 可能存在多个合法的拓扑序列。
入度：有多少边指向我，作用是判断顶点是否具备开始条件，入度 = 0：无任何前置边，是 “无依赖的起点”（如拓扑排序的初始节点、项目中的 “启动任务”）
出度：我有多少边指向别人，作用是判断顶点的后续影响范围，出度 = 0：无任何后续边，是 “无影响的终点”（如项目中的 “收尾任务”、课程链中的 “最终课程”）
有向无环图(DAG图)

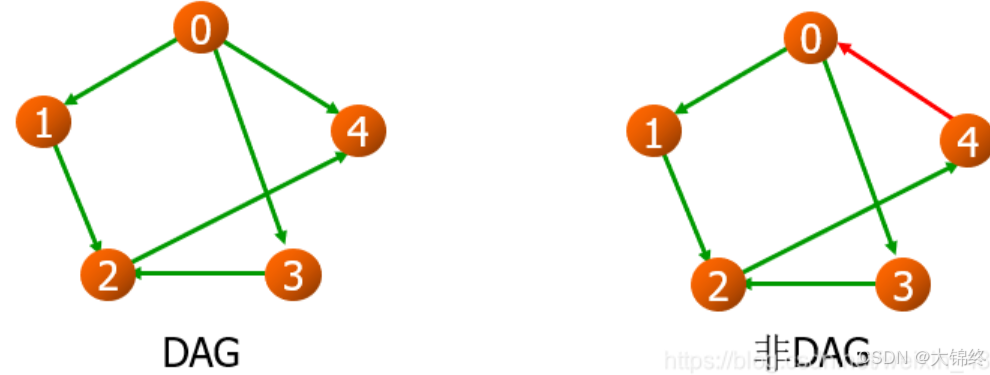
其中非DAG就是有环的
AOV网：顶点活动圈
在有向无环图中，用顶点来表示一个活动，用边来表示活动的先后顺序的图结构。价值是通过拓扑排序，将复杂的依赖关系转化为可执行的活动顺序，是解决 “依赖排序” 问题的经典模型
拓扑排序：
感性理解：找到做事情的先后顺序，排序的结果可能不是唯一的，因为入度为零的点不止一个
排序过程：
1.找出图中入度为0的点，然后输出
2.删除与该点连接的边
3.重复1、2操作，直到图中没有点或者没有入度为0(可能有环)的点为止
重要应用：判断有向图中是否有环
实现拓扑排序
借助队列来一次bfs即可
1.初始化：把所有入度为0的点加入到队列中
2.当队列不为空的时候：
拿出队头元素，加入到最终的结果当中
删除与该元素相连的边
判断：与删除边相连的点，是否入度变成0，如果入度变为0，加入到队列当中
如何建图

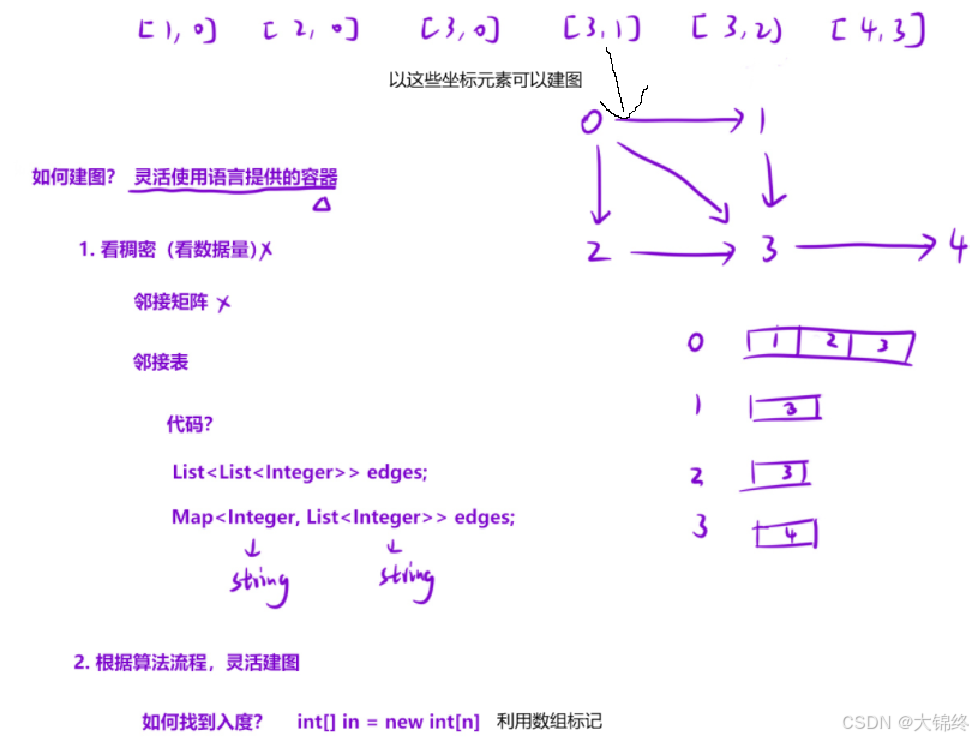
一. (207.) 课程表

在这里插入图片描述
原问题可以转换成⼀个拓扑排序问题。⽤ BFS 解决拓扑排序即可。

拓扑排序流程：
建图
将所有⼊度为 0 的点加⼊到队列中；
当队列不空的时候，⼀直循环：
i. 取出队头元素；
ii. 将于队头元素相连的顶点的⼊度 - 1；
iii. 然后判断是否减成 0,。如果减成 0，就加⼊到队列中。

class Solution {
public:bool canFinish(int n, vector<vector<int>>& p) {unordered_map<int,vector<int>> hash;//键图容器vector<int> in(n);//标识入度//1.建图for(auto &e:p){int x=e[0],y=e[1];//y是x的前置结点hash[y].push_back(x);in[x]++;}//2.拓扑排序bfsqueue<int>q;//把所有入度为0的点加入到队列中for(int e=0;e<n;e++)//注意这里要遍历的是元素的下标if(in[e]==0) q.push(e);//层序遍历while(q.size()){auto t=q.front();q.pop();//修改相连的边for(auto e:hash[t]){in[e]--;if(in[e]==0) q.push(e);}}//3.判断是否有环for(int i=0;i<n;i++){if(in[i]) return false;}return true;}
};

二. (210.) 课程表 II

在这里插入图片描述
和上题一样，多了一个返回执行顺序的最终数组

class Solution {
public:vector<int> findOrder(int n, vector<vector<int>>& p) {unordered_map<int,vector<int>> hash;vector<int> in(n);vector<int> ret;//建图for(auto &e:p){int x=e[0],y=e[1];hash[y].push_back(x);in[x]++;}//将前度为空的点入队列queue<int> q;for(int i=0;i<n;i++){if(in[i]==0) q.push(i);}//bfswhile(q.size()){int t=q.front();q.pop();//消除不相连的边并且加入最终队列ret.push_back(t);for(auto e:hash[t]){in[e]--;if(in[e]==0)  q.push(e);}}if(ret.size()==n) return ret;//返回数组元素大小等于原数组时证明可以拓扑排序else return {};}
};

三. (LCR 114.) 火星词典

在这里插入图片描述
题目意思是，假设火星词典中有a、b两个字符串，a在词典中排在b前面，遍历ab时出现不同的第一个位置的字符就是a中的小于b中的，特殊情况是a比b长，b长度内的字符都相等，就返回空。

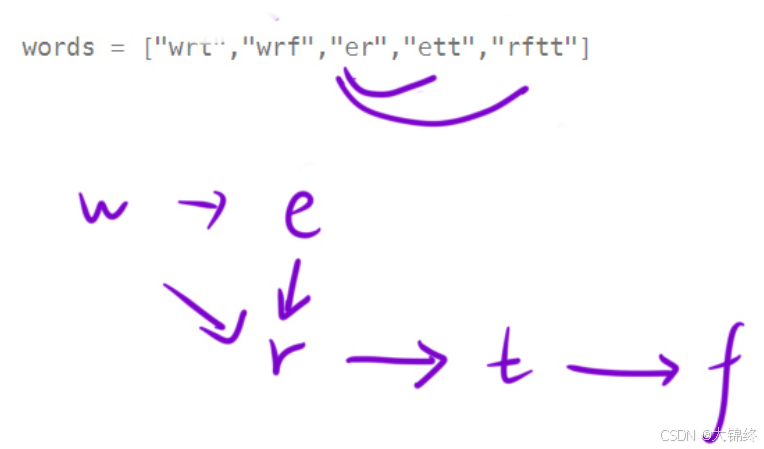
可以将每个字符的指向关系建图来表示，再通过拓扑排序

class Solution {unordered_map<char,unordered_set<char>> hash;//邻接表建图unordered_map<char,int> in;//统计入度bool check;
public:string alienOrder(vector<string>& words) {int n=words.size();//将出现过的元素入度初始化为0for(auto &e:words)//遍历每一个字符串{for(auto c:e)//遍历每一个字符{in[c]=0;}}//建图for(int i=0;i<n;i++)for(int j=i+1;j<n;j++){add(words[i],words[j]);if(check) return "";}//拓扑排序queue<char>q;string ret;//记录返回排序字符串for(auto &[a,b]:in){if(b==0) q.push(a);}while(q.size()){auto c=q.front();q.pop();ret+=c;for(auto e:hash[c]){if(--in[e]==0)q.push(e);}}//检查拓扑排序是否成功for(auto e:in){if(e.second!=0) return "";}return ret;}void add(const string&s1,const string &s2){int n=min(s1.size(),s2.size());//统计两字符串最小长度int i=0;for(;i<n;i++){if(s1[i]!=s2[i]){if(!hash.count(s1[i])||!hash[s1[i]].count(s2[i])){hash[s1[i]].insert(s2[i]);in[s2[i]]++;}break;}}//边界条件判断if(i==s2.size()&&s1.size()>s2.size()) check=true;}
};