当前位置：首页 > news >正文

数据结构系列之堆

news 2025/10/15 10:02:20

前言

堆是一种比较重要的数据结构,可以解决Top- K 问题，它也是优先级队列priority_queue的底层原理.

一、什么是堆？？？？

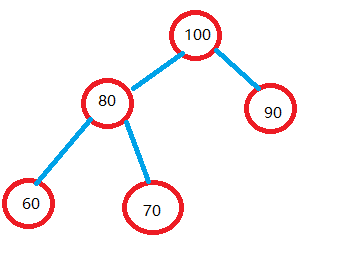
堆本质是一颗二叉树，并且是一棵完全二叉树 ! ! ! ! （其结点编号与相同深度的满二叉树对应位置一致）其中又分为大根堆和小根堆，大根堆—顾名思义:根比左孩子和右孩子的节点值都要大,小根堆相反.下面默认讲解的都是大根堆，因为堆的这个性质，根节点就是最大的节点.同时在每一颗子树中根节点都是最大的，由于这个性质,之后的排序算法之一就有一个堆排序(排序中讲).
对于下标：假如根节点的下标是i,左孩子的下标是2 * i + 1,右孩子的下标是2 * i + 2,孩子的节点的下标是i,父亲就是(i - 1) / 2
大根堆：
在这里插入图片描述

二、堆的操作

建堆（大堆）

给你一组数字,怎么建堆？？？核心操作：从第一个不为叶子的节点倒着向下调整,调整到根节点为止，什么是向下调整？堆的最核心条件是什么？？？父节点比子节点要大！所以,向下调整的思想就是：先找出左右孩子中比较大的那个，如果这个节点比父节点要大，就交换，然后继续往下走！否则直接break，一直调整到child >= n为止。
怎么找到第一个不为叶子的节点? ? ?
由于是完全二叉树，最后一个节点的父亲就一定是第一个不为叶子的节点，一共n个元素，最后一个节点的下标: n - 1 所以这个节点的下标就是(n - 1 - 1) / 2
比如拿1 5 3 8 7 6来建堆

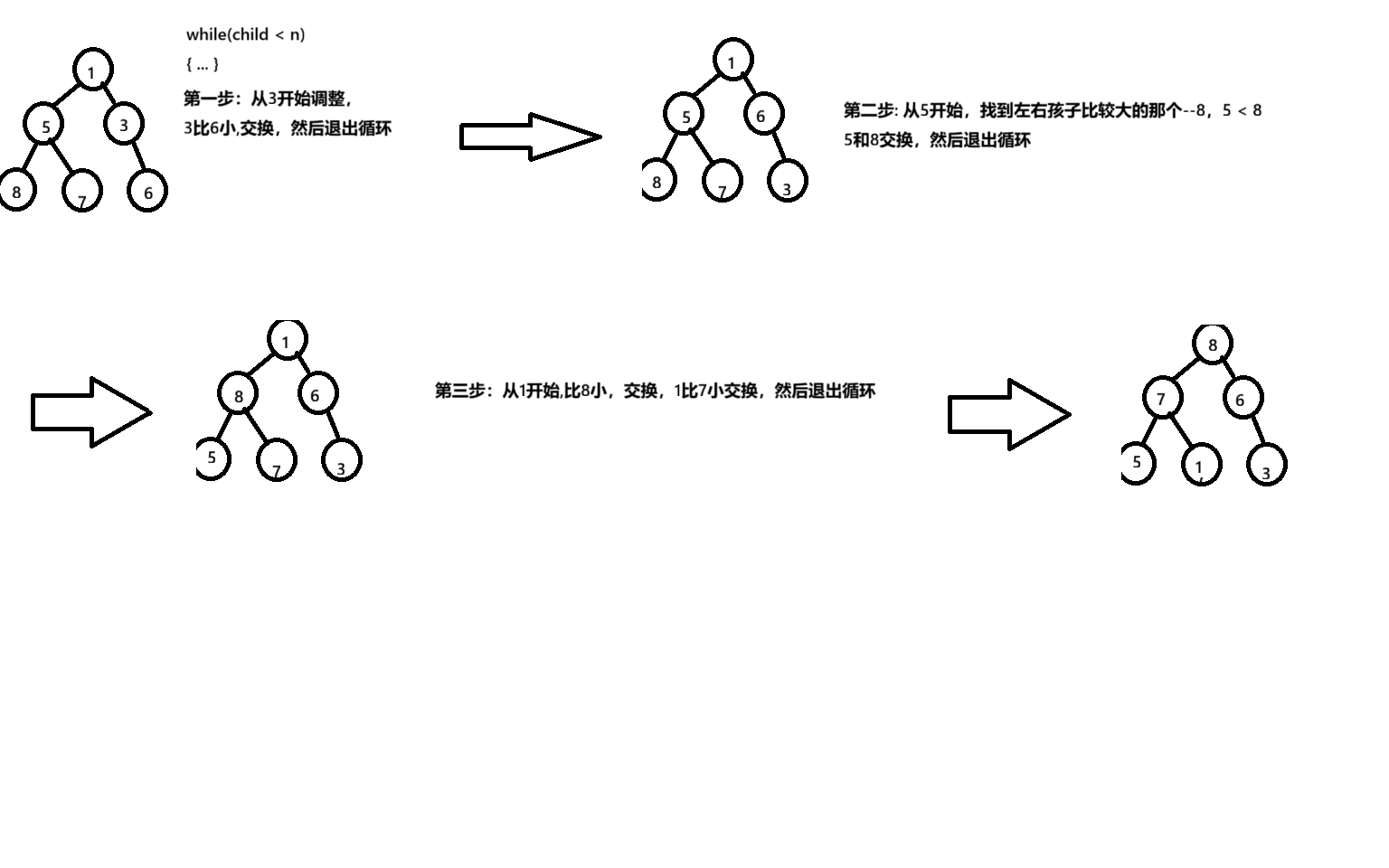
在这里插入图片描述

向下调整代码实现

void downAdjust(int* a,int n, int parent)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}

建堆代码实现

void HeapInitArray(HP* php, int* a, int n)
{assert(php);php->a = (int*)malloc(sizeof(int) * n);if (php->a == NULL){perror("malloc");return;}php->capacity = n;php->size = n;for (int i = (n - 2) / 2; i >= 0; i--){downAdjust(php->a, php->size, i);}
}

插入

push进去数据,向上调整即可，什么是向上调整，很好理解,向下调整反过来即可,从该节点往上比较，比父亲大就交换，然后继续向上,否则直接break；
这里不画图了,很好理解。

向上调整代码

void upAdjust(int* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] < a[child])//此处改为>即可变为小堆{Swap(&a[parent], &a[child]);child = parent;parent = (child - 1) / 2;}else{break; }}
}

插入代码

这里如果用容器适配器就简单的多了，调用一下vector的push_back()即可，用C实现的就是和顺序表一样的插入逻辑

void HeapPush(HP* php, int x)
{assert(php);if (php->size == php->capacity){int* tmp = (int*)realloc(php->a, sizeof(int) * php->capacity * 2);if (tmp == NULL){perror("realloc");return ;}php->a = tmp;php->capacity *= 2;}php->a[php->size] = x;php->size++;upAdjust(php->a,php->size - 1);
}

删除

删除操作指的是删除堆顶,直接删除合适吗？？？当然不合适，一删除所有的关系全都乱了，所以这里我们采用交换删除法，将堆顶和最后一个元素交换，出掉，然后向下调整堆顶。

删除代码

void HeapPop(HP* php)
{assert(php);assert(!HeapEmpty(php));Swap(&php->a[0], &php->a[php->size-1]);  //不取地址就去传引用php->size--;downAdjust(php->a,php->size, 0);
}