前端js 常见算法面试题目详解

一.哈希表法（两数之和）
哈希表法定义：
哈希表法 （Hash Table Method）是一种通过 哈希函数 将键值映射到数组索引的数据结构，支持快速插入、删除和查找操作，其时间复杂度接近O(1)（表示算法的执行时间与输入数据规模无关，即无论数据量大小，算法所需时间保持固定。）。 ‌
核心原理
哈希表通过哈希函数将键值映射到数组的特定位置，实现快速访问。例如，通过hash(key) = key % capacity（其中capacity为数组容量）计算位置，将数据存入对应索引。 ‌
题目：
找出数组目标值的索引？

const testArr = [12, 1, 7, 2, 5];
const twoSum = (nums, target) => {const map = new Map(); // 构建map键值对 对象for (let i = 0; i < nums.length; i++) { // 遍历目标数组const complement = target - nums[i]; // 7,17,12 //算出目标值与当前值相减的补数console.log(complement, map.has(complement), map.get(complement), map, 'complementcomplement');if (map.has(complement)) return [map.get(complement), i]; // 当条件为true时 返回索引和当前值的索引即为两数之和的索引map.set(nums[i], i); // 不满足条件则存储数值与索引的映射关系{12: 0, 1: 1, 7: 2}}
};console.log(twoSum(testArr, 9), '9为目标值');
// 打印结果[2,3]
// 时间复杂度 O(n)，空间复杂度 O(n)‌:ml-citation{ref="1" data="citationList"}

二.字母异位词分组
题目：
给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。
思路：

1. 创建一个空对象来存储每个字母异位词组。
2. 用for of 遍历字符串数组，对每个字符串进行排序（因为排序后的字符串是相同的，可以用来作为键）。
3. 使用排序后的字符串作为键，原始字符串作为值，存储到哈希表中。
4. 收集所有具有相同键的值，即为同一组字母异位词。
5. 返回这些分组。

function groupAnagrams(strs) {const anagramGroups = {};for (const str of strs) {// 将数组中每个字符串转换为字符数组，排序，再转回字符串作为键const sortedStr = str.split('').sort().join('');// 如果该键尚不存在于对象中，初始化一个空数组if (!anagramGroups[sortedStr]) {anagramGroups[sortedStr] = [];}// 将原始字符串添加到排序后相同的键值对应组的数组中anagramGroups[sortedStr].push(str);}// 返回所有组的数组形式return Object.values(anagramGroups);
}// 示例使用
const strings = ["eat", "tea", "tan", "ate", "nat", "bat"];
console.log(groupAnagrams(strings));
输出结果：[["bat"], ["eat", "tea", "ate"], ["tan", "nat"]]

总结
这段代码首先创建了一个空对象anagramGroups来存储字母异位词组。然后，它遍历输入的字符串数组，对每个字符串进行排序，并以排序后的字符串作为键存储到哈希表中。最后，它使用Object.values()方法获取所有值（即所有字母异位词组），并返回这些值。
三.最长连续序列
题目：
给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。
请你设计并实现时间复杂度为 O(n) (算法的执行时间随输入数据规模n的增大而呈线性增长)的算法解决此问题。
线性增长特性‌：当输入数据量n增加时，算法的执行时间（或基本操作次数）以相同比例增加。例如，若n增大10倍，执行时间也近似增大10倍
思路：

1. 排序数组‌：使用Arrays.sort(nums)对数组进行排序，确保数字按升序排列。 ‌
2. 初始化变量‌：设置longestLen为1（初始序列长度），len为当前连续序列长度。 ‌ ‌遍历数组‌：从第二个元素开始（i =1），比较当前元素与前一个元素的大小：
   若相等（nums[i] === nums[i-1]），则连续性中断，重置len = 1； 若相差1（nums[i] - nums[i-1] =1），则len++；
3. 每次循环更新longestLenMath.max(longestLen, len)，保留最长序列。 ‌ ‌返回结果‌：最终longestLen即为最长连续序列的长度。

function longestConsecutive(numsArr) {if (numsArr.length === 0) return 0;const nums = numsArr.sort((a, b) => a - b);let longestLen = 1;let len = 1;for (let i = 1; i <= nums.length; i++) {if (nums[i] === nums[i-1]) continue; // 相同数字不增加连续性const numValue = nums[i] - nums[i - 1];if (numValue === 1){len = len + 1;} else {len = 1;}longestLen = Math.max(longestLen, len); // 两数相比取大值}return longestLen;
}const nums = [100,4,200,1,3,2]
const longLength = longestConsecutive(nums) // 4// 输入：nums = [100,4,200,1,3,2]
// 输出：4
// 最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

四.双指针（移动零）
双指针定义：
双指针法是一种通过设置两个指针（或索引）遍历数据结构，利用指针移动规则优化算法效率的通用算法思想，主要用于减少不必要的循环次数，降低时间复杂度，降低空间复杂度。
核心思想
双指针法通过两个指针同步或异步移动来解决问题，适用于有序数据结构（如数组、链表）。常见类型包括：

• ‌对撞指针‌：从两端向中间移动（如反转字符串或查找元素对） ‌
• 快慢指针‌：以不同速度移动（如检测环形链表或数组去重）
  题目：
  给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。
  请注意 ，必须在不复制数组的情况下原地对数组进行操作。
  思路：
  使用两个指针，一个用于遍历原数组，另一个用于在遍历过程中填充非零元素到正确的位置
  1.定义上一个非零元素的索引位置为0
  2.遍历数组如果元素不为0将非零元素移到前面，并更新lastNonZeroFoundAt的位置
  [nums[i], nums[lastNonZeroFoundAt]] = [nums[lastNonZeroFoundAt], nums[i]];
  3.不为0索引+1
  4.直接返回原数组

//列子：const nums = [0, 1, 0, 3, 12];
function moveZerosToEnd(nums) {let lastNonZeroFoundAt = 0; // 上一个非零元素的索引位置for (let i = 0; i < nums.length; i++) { //i 为当前索引位置if (nums[i] !== 0) {//i: 1,3,4// 将非零元素移到前面，并更新lastNonZeroFoundAt的位置[nums[i], nums[lastNonZeroFoundAt]] = [nums[lastNonZeroFoundAt], nums[i]]; // =号前面为交换后新位置 =后面为原始位置,移动到前面的元素的原位置需要0来补位// [1,0]=[0,1] [1,0,0,3,12] 索引1放索引0 原索引1补0// [3,0]=[0,3] [1,3,0,0,12] 索引3放索引1 原索引3补0// [12,0]=[0,12] [1,3,12,0,0] 索引4方索引2 原索引4补0lastNonZeroFoundAt++; //0,1,2}}return nums; // 直接修改原数组并返回
}
console.log(moveZerosToEnd(nums))
//打印结果 [1,3,12,0,0]

五.盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

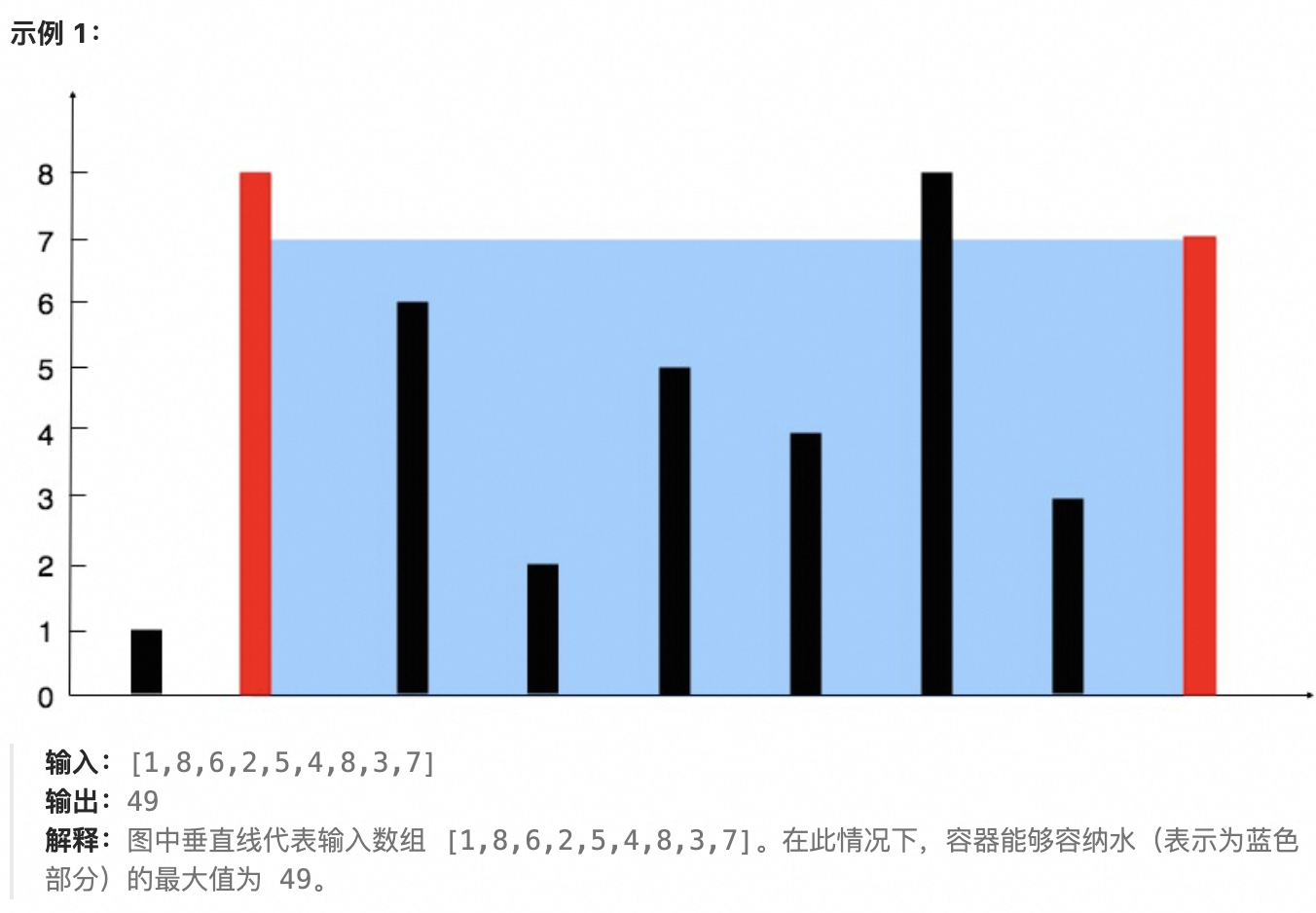
思路：
1.积水面积Math.abs(Math.min(height[left], height[right]) * (left - right))，左指针 left 指向数组起始（索引 0 ），右指针 right 指向数组末尾（索引 height.length - 1 ）。 //Math.abs:绝对值
水容量 = 两条线段中较矮的高度 × 线段间水平距离
2. 每次取 left 和 right 对应高度的较小值（矮的柱子决定了容器的高度 ），乘以指针间距（水平距离（ 宽度）），得到当前容器容量，再和历史最大容量 res 比较，更新 res。
3.若 height[left] < height[right]，说明左指针对应的线段更矮，固定右指针时，左指针右移可能找到更高线段，让容量更大，所以 left++；反之，right-- 。重复此过程，直到 left >= right ，遍历结束，此时 res 就是最大容量。

function maxArea(height) {let left = 0;//[1,8,6,2,5,4,8,3,7]let right = height.length - 1; //8,7,6,5,4,3,2,1let res = 0; // 历史最大容量while (left < right) {res = Math.max(res, Math.abs(Math.min(height[left], height[right]) * (left - right)));// 历史最大容量，当前遍历到的两个柱子的容量console.log(res,'resssssssss');if (height[left] < height[right]) {left++;// 左指针右移动} else {right--; // 右指针左移}}return res;
}console.log(maxArea([1,8,6,2,5,4,8,3,7]),'kkkkkkk')
// 49

总结：算出每两条柱子的容量，最后取最大值