算法9.0

209. 长度最小的子数组 - 力扣（LeetCode）

开始滑动窗口专题：

什么是 什么时候用：  同向双指针 暴力解法时发现两个指针都是同一个方向移动的时候

正确性：单调性  规避了许多不必要的枚举

滑动窗口的时间复杂度 ： 最差是n方 根据实际情况分析时间复杂度  

如何使用代码：实际情况分析

做题的目标是把暴力解法优化

解法一：

暴力解法：枚举所有的子数组 然后求和  然后判断 （时间复杂度很高 n的立方）

如何优化暴力解法呢

发现的规律一：

单调性  ：先固定一个左区间  sum统计以left为左区间的和(sum省去从前往后的区间）

                 右区间一直走  同时看sum的值如果大于了target  就已经找到一个结果

               （要长度最小的子数组 长度这关就卡住了 所以这个右区间就可以停了）

 

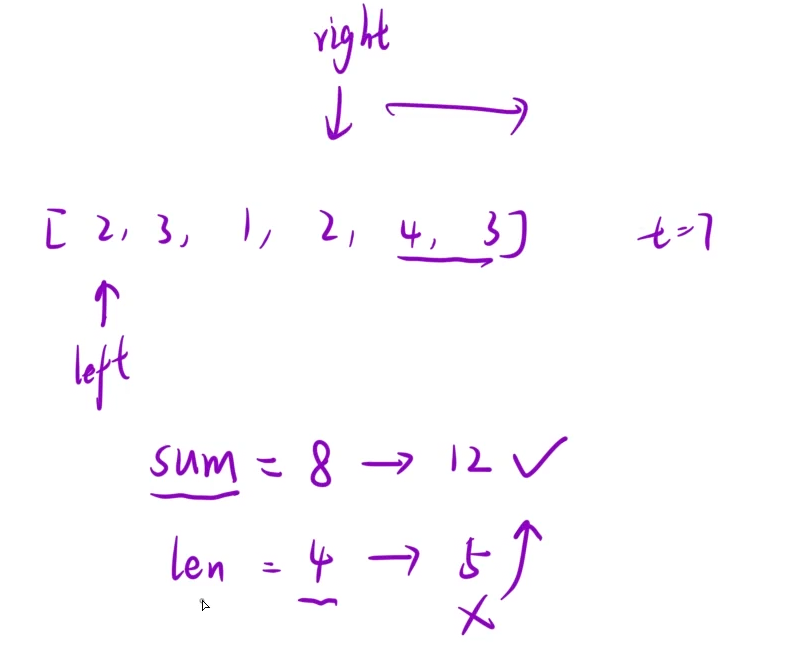
发现的规律二：

left移动后  sum有前面的值  只需要将sum减去left移动前的数字 就是当下真正的sum

不用把right拉回去重新一次次计算

解法二：利用单调性 使用同向双指针 来优化

同向双指针 ：双指针往同一个方向移动  同向窗口也称为"滑动窗口"

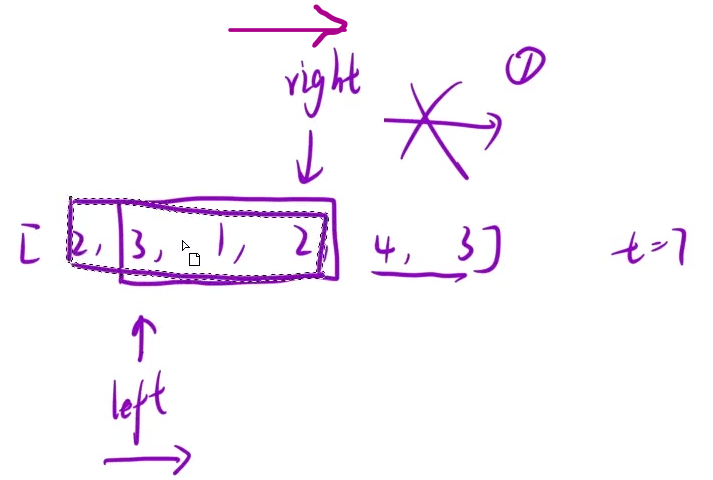
进窗口是维护窗口的信息   在这里指的是sum的值   sum和target判断   合适了就出窗口

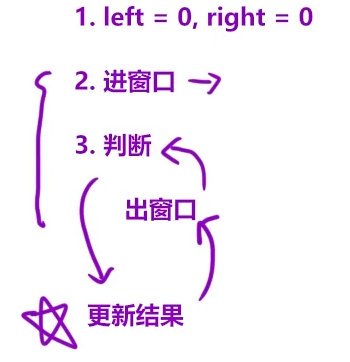
2 3步是循环 进窗口是right++   出窗口是left++

正确性：为什么滑动窗口这个过程能更新出来最终结果？

隐秘的点在单调性里面 

虽然没有枚举了所有情况 但是利用单调性规避了很多没有必要的枚举行为

下面是效果图和代码：

class Solution {public int minSubArrayLen(int target, int[] nums) {//排序//Arrays.sort(nums); 题目要求的是原始数组的连续子数组 排序后数组顺序改变 导致子数组不连int n = nums.length;int len= Integer.MAX_VALUE;//因为要求的是len的最小值 如果初始化定义为0可能返回0  //所以修改为 int len = Integer.Max_Value;//right-left+1; 后面需要更新就补药写到外面 写到循环里面int sum=0; //nums[left] + nums[right] ;for(int left=0,right=0;right<n;right++){sum += nums[right] ;//进窗口while(sum>=target){//判断len= Math.min(len,right-left+1);//更新结果sum -= nums[left++];//顺便出窗口}}return len == Integer.MAX_VALUE ? 0:len;}
}
//xiyu20251014&1#2*1//定义len的细节问题
//进窗口的循环条件 right<n  不是我想的那样固定一个数遍历完数组然后固定数++的
//更新len的时候 直接用math的那个函数就可以了  不用自己写一个求最小的方法
//返回len的时候 注意特殊情况