Java优选算法——位运算
常见位运算总结
1.基础位运算
<<:表示左移
>>:表示右移
~:表示每一位取反
&:表示“且”,有0则0
|:表示“或”,有1则1
^:异或操作,相同为0,相异为1(无进位相加)
2.给一个数,确定它的二进制表示中的第x位是0还是1
计算(n>>x)&1
- 为1:第x位是1
- 为0:第x位是0
3.将一个数n的二进制表示的第x位修改成1
n=n|(1<<x)
4.将一个数n的二进制表示的第x位修改成0
n=n&(~(1<<x))
5.提取一个数n二进制表示中最右侧的1
只提取出最右边的1,说明左边的可以不要(为0)
n&-n
6.去掉一个数n二进制表示中最右侧的1
只去掉最右边的1,说明左边的不变
n&(n-1)
一、判断字符是否唯一
题目链接:https://leetcode.cn/problems/is-unique-lcci/description/
题目:
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:输入:s = "leetcode"输出:false
示例 2:输入:s = "abc"输出:true
限制:
- 0<=len(s)<=100
- s [i] 仅包含小写字母
- 如果你不使用额外的数据结构,会很加分。
思路:
这道题使用了位图的思想。
我们需要一个数bitmap=0,让它的每一个二进制位的数字来表示字母是否出现过。
首先:如果字符串的长度大于26,那必定有重复的字符出现。
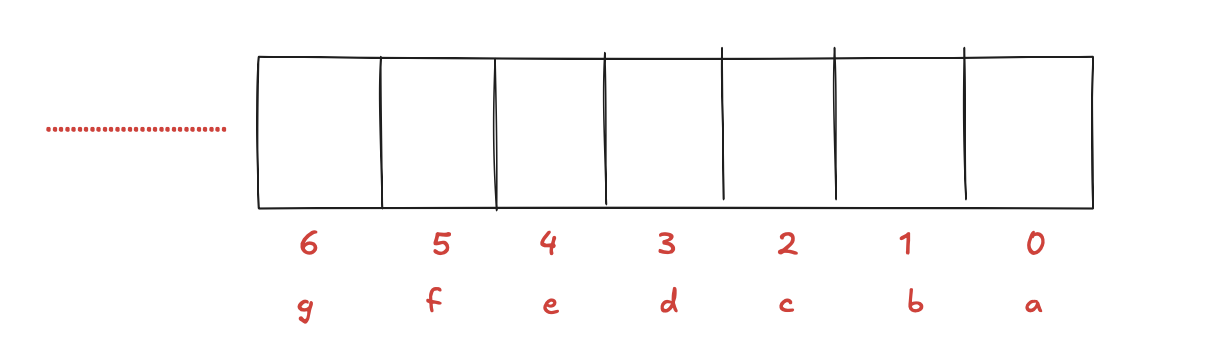
当我们遍历字符串时,拿出对应的字符找到在位图中对应的位置,判断该位置是否为1,如果为1,说明这个字符串是重复了的,返回false;如果为0,则将位图中对应的位置修改为1,直到遍历完整个字符串。
代码及结果:
class Solution {public boolean isUnique(String astr) {if(astr.length()>26) return false;int bitmap=0;//建立一个位图,有32位//对应字符位置的元素为1,则说明有该字符for(int i=0;i<astr.length();i++){int x=astr.charAt(i)-'a';//判断位图中是否有该字符if(((bitmap>>x)&1)==1) return false;//将该字符加入到位图中bitmap|=1<<x;}return true;}
}二、
题目链接:https://leetcode.cn/problems/missing-number/
题目:
给定一个包含 [0,n] 中 n 个数的数组 nums,找出 [0,n] 这个范围内没有出现在数组中的那个数。
示例 1:
输入:nums=[3,0,1]
输出:2
解释:n=3,因为有 3 个数字,所以所有的数字都在范围 [0,3] 内。2 是丢失的数字,因为它没有出现在 nums中。
示例 2:
输入:nums=[0,1]
输出:2
解释:n=2,因为有 2 个数字,所以所有的数字都在范围 [0,2] 内。2 是丢失的数字,因为它没有出现在 nums中。
示例 3:
输入:nums=[9,6,4,2,3,5,7,0,1]
输出:8
解释:n=9,因为有 9 个数字,所以所有的数字都在范围 [0,9] 内。8 是丢失的数字,因为它没有出现在 nums中。
思路:
使用位运算中的异或运算(无进位相加)。
把数组中所有元素异或起来,再将0~n的所有数也异或起来,就能两两消除相同的数。
代码及结果:
class Solution {public int missingNumber(int[] nums) {int sum=0;for(int i=0;i<nums.length;i++){sum=sum^(nums[i]^i);}sum=sum^nums.length;return sum;}
}三、两整数之和
题目链接:https://leetcode.cn/problems/sum-of-two-integers/
题目:
给你两个整数 a 和 b,不使用运算符 + 和 -,计算并返回两整数之和。
示例 1:输入:a = 1,b = 2输出:3
示例 2:输入:a = 2,b = 3输出:5
思路:
本题要求不能使用运算符,所以使用位运算解决。
首先,使用无进位相加a^b,
至于进位操作:在异或结果的基础上找出哪些是需要进位的(a&b)<<1,
将a^b作为新的a,将(a&b)<<1作为新的b,继续重复以上操作,直到不需要进位,即b为0。
代码及结果:
class Solution {public int getSum(int a, int b) {while(b!=0){int x=a^b;//先计算出a和b无进位相加结果b=(a&b)<<1;a=x;}return a;}
}四、只出现一次的数字Ⅱ
题目链接:https://leetcode.cn/problems/single-number-ii/description/
题目:
给你一个整数数组 nums,除某个元素仅出现一次外,其余每个元素都恰出现三次。请你找出并返回那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。
示例 1:输入:nums = [2,2,3,2]输出:3
示例 2:输入:nums = [0,1,0,1,0,1,99]输出:99
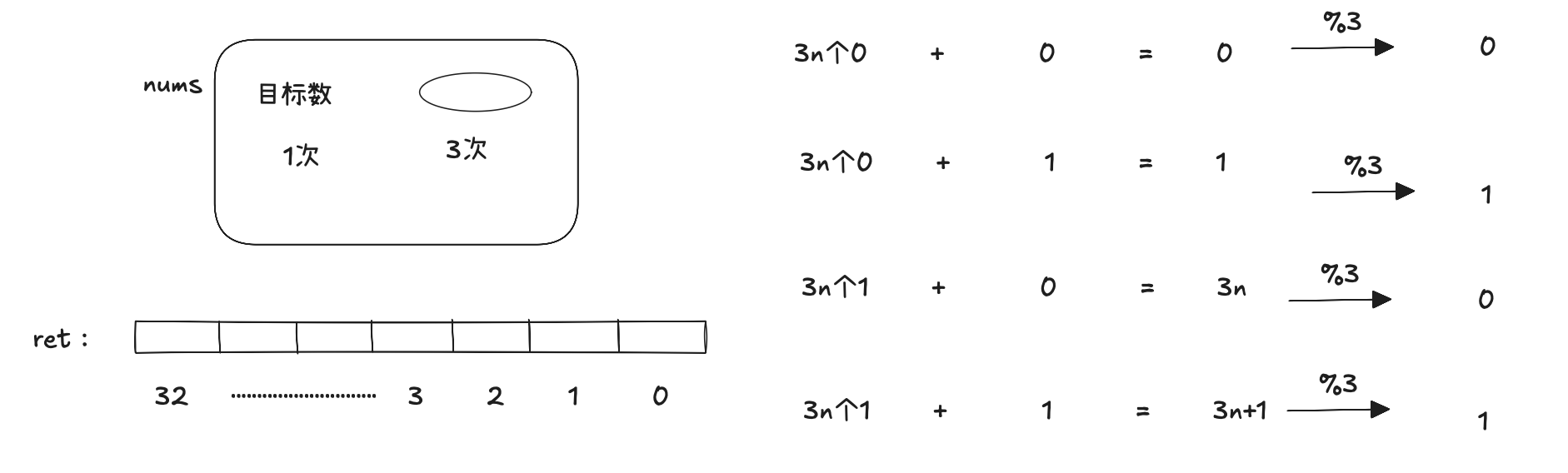
思路:
除目标数外,每一个数的二进制的每一位要么为0要么为1,则所有数的对应的二进制位数相加,应该为3n个0或者3n个1(n表示整数),将其与目标数的对应二进制位相加后%3:
当结果为0,则目标数该位数为0;
当结果为1,则目标数该位数为1;
代码及结果:
class Solution {public int singleNumber(int[] nums) {int ret=0;//要查找的那个数字for(int i=0;i<32;i++){//依次遍历位图的每一位int sum=0;//用于存放所有数字第i位之和for(int x:nums){if(((x>>i)&1)==1){sum++;}}ret=ret^((sum%3)<<i);}return ret;}
}
五、消失的两个数字
题目链接:https://leetcode.cn/problems/missing-two-lcci/
题目:
给定一个数组,包含从 1 到 N 所有的整数,但其中缺了两个数字。你能在 O (N) 时间内只用 O (1) 的空间找到它们吗?
以任意顺序返回这两个数字均可。
示例 1:输入:[1]输出:[2,3]
示例 2:输入:[2,3]输出:[1,4]
思路:
这道题依旧使用位运算的思想,我们将数组和1~N之间的数都异或起来,这时得到的数为x1和x2的异或。
首先x1和x2一定不相等,所以x1和x2异或的结果的二进制位中一定有“1”,假设1在第x位,则x1在x位的数是与x2的不同的。
假设x1在x位为0,x2在x位为1,我们再将所有的数分为两类:
一类在x位为0,它们异或之后结果就为x1;
一类在x位为1,它们异或之后结果就为x2.
代码及结果:
class Solution {public int[] missingTwo(int[] nums) {int ans[]=new int[2];//转化为:只出现一次的数字3int ret=0;//存放x1^x2int n=nums.length;for(int x:nums){ret^=x;}for(int i=1;i<=n+2;i++){ret^=i;}//此时ret=x1^x2;//在nums中和1到N的所有数中找到x1和x2//1 先找到ret中最右边的1所在位置ret=ret&(-ret);int x1=0,x2=0;//说明x1和x2在这个位置的值不一样,假如x1此处为0,x2此处为1for(int x:nums){if((x&ret)==0){//说明x在这个位置的数为0,与x1分为一类x1^=x;}else{x2^=x;}}for(int i=1;i<=n+2;i++){if((i&ret)==0){//说明x在这个位置的数为0,与x1分为一类x1^=i;}else{x2^=i;}}ans[0]=x1;ans[1]=x2;return ans;}
}