5. 神经网络的学习
1.从数据中学习
神经网络的特征就是可以从数据中学习。所谓“从数据中学习”,是指
可以由数据自动决定权重参数的值。这是非常了不起的事情!因为如果所有
的参数都需要人工决定的话,工作量就太大了。在第2章介绍的感知机的例
子中,我们对照着真值表,人工设定了参数的值,但是那时的参数只有3个。
而在实际的神经网络中,参数的数量成千上万,在层数更深的深度学习中,
参数的数量甚至可以上亿,想要人工决定这些参数的值是不可能的。本章将
介绍神经网络的学习,即利用数据决定参数值的方法,并用Python实现对
MNIST手写数字数据集的学习。
机器学习中,一般将数据分为训练数据和测试数据两部分来进行学习和
实验等。首先,使用训练数据进行学习,寻找最优的参数;然后,使用测试
数据评价训练得到的模型的实际能力。为什么需要将数据分为训练数据和测
试数据呢?因为我们追求的是模型的泛化能力。为了正确评价模型的泛化能
力,就必须划分训练数据和测试数据。另外,训练数据也可以称为监督数据。
泛化能力是指处理未被观察过的数据(不包含在训练数据中的数据)的
能力。获得泛化能力是机器学习的最终目标。比如,在识别手写数字的问题
中,泛化能力可能会被用在自动读取明信片的邮政编码的系统上。此时,手
写数字识别就必须具备较高的识别“某个人”写的字的能力。注意这里不是“特
定的某个人写的特定的文字”,而是“任意一个人写的任意文字”。如果系统
只能正确识别已有的训练数据,那有可能是只学习到了训练数据中的个人的
习惯写法。
因此,仅仅用一个数据集去学习和评价参数,是无法进行正确评价的。
这样会导致可以顺利地处理某个数据集,但无法处理其他数据集的情况。顺
便说一下,只对某个数据集过度拟合的状态称为过拟合(over fitting)。避免
过拟合也是机器学习的一个重要课题。
2.损失函数
神经网络的学习中所用的指标称为损失函数(loss function)。这个损失函数可以使用任意函数,但一般用均方误差和交叉熵误差等。
损失函数是表示神经网络性能的“恶劣程度”的指标,即当前的
神经网络对监督数据在多大程度上不拟合,在多大程度上不一致。
以“性能的恶劣程度”为指标可能会使人感到不太自然,但是如
果给损失函数乘上一个负值,就可以解释为“在多大程度上不坏”,
即“性能有多好”。并且,“使性能的恶劣程度达到最小”和“使性
能的优良程度达到最大”是等价的,不管是用“恶劣程度”还是“优
良程度”,做的事情本质上都是一样的。

比如,在3.6节手写数字识别的例子中, yk、 tk是由如下10个元素构成的数据。
>>> y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
>>> t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
数组元素的索引从第一个开始依次对应数字“0”“1”“2”…… 这里,神
经网络的输出y是softmax函数的输出。由于softmax函数的输出可以理解为
概率,因此上例表示“0”的概率是0.1,“1”的概率是0.05,“2”的概率是0.6
等。 t是监督数据,将正确解标签设为1,其他均设为0。这里,标签“2”为1,
表示正确解是“2”。将正确解标签表示为1,其他标签表示为0的表示方法称
为one-hot表示。
如式(4.1)所示,均方误差会计算神经网络的输出和正确解监督数据的各个元素之差的平方,再求总和。现在,我们用Python来实现这个均方误差,实现方式如下所示。
# 1_mean_squared_error.py
import numpy as np
import matplotlib.pyplot as pltdef mean_squared_error(y, t):return 0.5 * np.sum((y-t)**2)t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]# 例1: “2”的概率最高的情况(0.6)
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
error = mean_squared_error(np.array(y), np.array(t))
print(error) # 0.09750000000000003# 例2: “7”的概率最高的情况(0.6)
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
error = mean_squared_error(np.array(y), np.array(t))
print(error) # 0.5975
发现第一个例子的损失函数的值更小,和监督数据之间的
误差较小。也就是说,均方误差显示第一个例子的输出结果与监督数据更加吻合。
交叉熵误差
除了均方误差之外, 交叉熵误差(cross entropy error)也经常被用作损
失函数。交叉熵误差如下式所示。
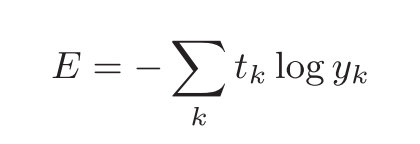
这里, log表示以e为底数的自然对数(log e)。 yk是神经网络的输出, tk是
正确解标签。并且, tk中只有正确解标签的索引为1,其他均为0(one-hot表示)。
因此,式(4.2)实际上只计算对应正确解标签的输出的自然对数。比如,假设
正确解标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差
是-log 0.6 = 0.51;若“2”对应的输出是0.1,则交叉熵误差为-log 0.1 = 2.30。
也就是说,交叉熵误差的值是由正确解标签所对应的输出结果决定的。
自然对数的图像如图4-3所示。
式(4.2)实际上只计算对应正确解标签的输出的自然对数。比如,假设
正确解标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差
是-log 0.6 = 0.51;若“2”对应的输出是0.1,则交叉熵误差为-log 0.1 = 2.30。
也就是说,交叉熵误差的值是由正确解标签所对应的输出结果决定的。
# 2_log.py
import numpy as np
import matplotlib.pyplot as pltx = np.arange(0,1,0.01)
y = np.log(x)plt.plot(x,y,label="log")
plt.xlabel("x")
plt.ylabel("y")
plt.title('y=logx')
plt.legend()
plt.show()
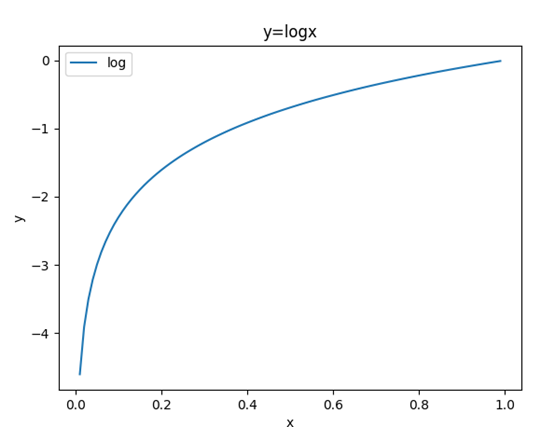
x: 表示正确解标签对应的神经网络的输出
y: 是对应的logx,
神经网络的输出越趋近于1(即概率越大),则输出趋于0,交叉熵
误差为0
如果神经网络的输出趋近于0,则输出趋近于无穷大。
下面,我们来用代码实现交叉熵误差。
# 3_cross_entropy_error.py
import numpy as np
import matplotlib.pyplot as pltdef cross_entropy_error(y, t):delta = 1e-7return -np.sum(t * np.log(y+delta))t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]# 例1: “2”的概率最高的情况(0.6)
y = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
error = cross_entropy_error(np.array(y), np.array(t))
print(error) # 0.510825457099338# 例2: “7”的概率最高的情况(0.6)
y = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
error = cross_entropy_error(np.array(y), np.array(t))
print(error) # 2.302584092994546
这里,参数y和t是NumPy数组。函数内部在计算np.log时,加上了一
个微小值delta。这是因为,当出现np.log(0)时, np.log(0)会变为负无限大的-inf,这样一来就会导致后续计算无法进行。作为保护性对策,添加一个微小值可以防止负无限大的发生。
正确解标签对应的输出为0.6,此时的交叉熵误差大约
为0.51。第二个例子中,正确解标签对应的输出为0.1的低值,此时的交叉
熵误差大约为2.3。由此可以看出,这些结果与我们前面讨论的内容是一致的。
3.mini-batch学习
机器学习使用训练数据进行学习。使用训练数据进行学习,严格来说,
就是针对训练数据计算损失函数的值,找出使该值尽可能小的参数。因此,
计算损失函数时必须将所有的训练数据作为对象。也就是说,如果训练数据
有100个的话,我们就要把这100个损失函数的总和作为学习的指标。
前面介绍的损失函数的例子中考虑的都是针对单个数据的损失函数。如果要求所有训练数据的损失函数的总和,以交叉熵误差为例,可以写成下面
的式(4.3)。
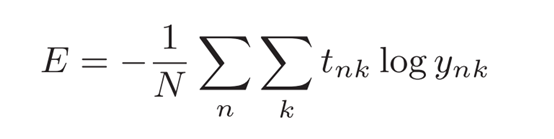
这里,假设数据有N个, tnk表示第n个数据的第k个元素的值(ynk是神
经网络的输出, tnk是监督数据)。式子虽然看起来有一些复杂,其实只是把
求单个数据的损失函数的式(4.2)扩大到了N份数据,不过最后还要除以N
进行正规化。通过除以N,可以求单个数据的“平均损失函数”。通过这样的
平均化,可以获得和训练数据的数量无关的统一指标。比如,即便训练数据
有1000个或10000个,也可以求得单个数据的平均损失函数。
另外, MNIST数据集的训练数据有60000个,如果以全部数据为对象
求损失函数的和,则计算过程需要花费较长的时间。再者,如果遇到大数据,
数据量会有几百万、几千万之多,这种情况下以全部数据为对象计算损失函
数是不现实的。因此,我们从全部数据中选出一部分,作为全部数据的“近
似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch,小
批量),然后对每个mini-batch进行学习。比如,从60000个训练数据中随机
选择100笔,再用这100笔数据进行学习。这种学习方式称为mini-batch学习。
下面我们来编写从训练数据中随机选择指定个数的数据的代码,以进行
mini-batch学习。在这之前,先来看一下用于读入MNIST数据集的代码。
# 4_mini_batch.py
import sys, os
import pickle
import numpy as np
sys.path.append(os.pardir)
from dataset.mnist import load_mnist(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape)
print(t_train.shape)
train_size = x_train.shape[0]
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
print(batch_mask)
print(x_batch)
print(t_batch)
4.mini-batch版交叉熵误差的实现
如何实现对应mini-batch的交叉熵误差呢?只要改良一下之前实现的对
应单个数据的交叉熵误差就可以了。这里,我们来实现一个可以同时处理单
个数据和批量数据(数据作为batch集中输入)两种情况的函数。
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
当监督数据是标签形式(非one-hot表示,而是像“2”“7”这样的标签)时,交叉熵误差可通过如下代码实现

5. 为何要设定损失函数
在神经网络的学习中,寻找最优参数(权重和偏置)时,
要寻找使损失函数的值尽可能小的参数。为了找到使损失函数的值尽可能小
的地方,需要计算参数的导数(确切地讲是梯度),然后以这个导数为指引,
逐步更新参数的值。
6.数值微分
利用微小的差分求导数的过程称为数值微分(numerical differentiation)。
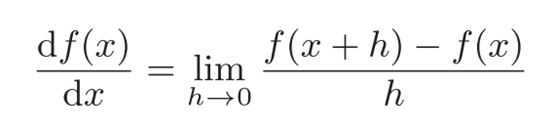
x的“微小变化”将导致函数f(x)的值在多大程度上发生变化。
def numerical_diff(f, x):h = 1e-4 # 0.0001return (f(x+h) - f(x-h)) / (2*h)
y = 0.01x2 + 0.1x
def function_1(x):return 0.01*x**2 + 0.1*x
x = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
plt.show()
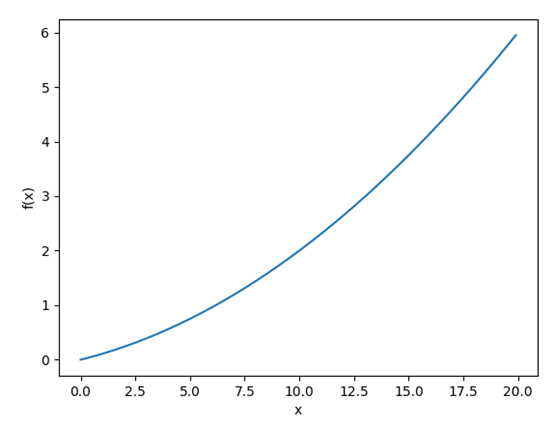
计算一下这个函数在x = 5和x = 10处的导数。
# 6_numerical_diff.py
import numpy as np
import matplotlib.pyplot as pltdef numerical_diff(f, x):h = 1e-4 # 0.0001return (f(x+h) - f(x-h)) / (2*h)def function_1(x):return 0.01*x**2 + 0.1*xx = np.arange(0.0, 20.0, 0.1)
y = function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
plt.show()d1 = numerical_diff(function_1, 5)
d2 = numerical_diff(function_1, 10)
print(d1) # 0.1999999999990898
print(d2) # 0.2999999999986347
7.偏导数
f(x0,x1) = x02+x12
def function_2(x):return x[0]**2 + x[1]**2
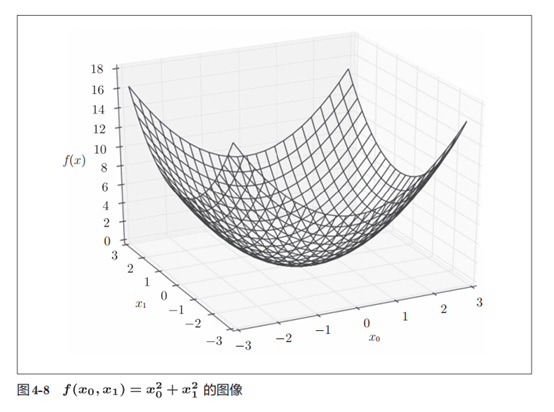

# 或者 return np.sum(x**2)def function_2(x):return x[0]**2 + x[1]**2
# 或者 return np.sum(x**2)def function_tmp1(x0):return x0*x0 + 4.0**2.0def function_tmp2(x1):return 3.0**2.0 + x1*x1d3 = numerical_diff(function_tmp1, 3)
d4 = numerical_diff(function_tmp2, 4)
print(d3) # 6.00000000000378
print(d4) # 7.999999999999119
8.梯度

# 7_numerical_gradient.py
import numpy as np
import matplotlib.pyplot as pltdef function_2(x):return x[0]**2 + x[1]**2
# 或者 return np.sum(x**2)def numerical_gradient(f, x):h = 1e-4 # 0.0001grad = np.zeros_like(x) # 生成和形状相同的数组print(x.shape)print(x.size)for idx in range(x.size):tmp_val = x[idx]x[idx] = tmp_val + hfxh1 = f(x)x[idx] = tmp_val - hfxh2 = f(x)grad[idx] = (fxh1 - fxh2) / (2*h)x[idx] = tmp_val # 还原值return gradd1 = numerical_gradient(function_2,np.array([3.0, 4.0]))
d2 = numerical_gradient(function_2,np.array([0.0, 2.0]))
d3 = numerical_gradient(function_2,np.array([3.0, 0.0]))
print(d1) # [6. 8.]
print(d2) # [0. 4.]
print(d3) # [6. 0.]
我们可以计算(x0, x1)在各点处的梯度。上例中,点(3, 4)处的
梯度是(6, 8)、点(0, 2)处的梯度是(0, 4)、点(3, 0)处的梯度是(6, 0)。这个
梯度意味着什么呢?
梯度指示的方向是各点处的函数值减小最多的方向。
9.梯度法
机器学习的主要任务是在学习时寻找最优参数。同样地,神经网络也必
须在学习时找到最优参数(权重和偏置)。这里所说的最优参数是指损失函数 取最小值时的参数。但是,一般而言,损失函数很复杂,参数空间庞大,我
们不知道它在何处能取得最小值。而通过巧妙地使用梯度来寻找函数最小值
(或者尽可能小的值)的方法就是梯度法。
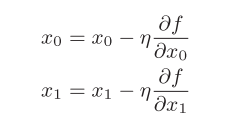
η表示更新量,在神经网络的学习中,称为学习率(learning
rate)。学习率决定在一次学习中,应该学习多少,以及在多大程度上更新参数。
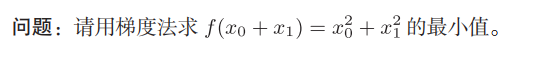
# 8_gradient_descent.py
import numpy as np
import matplotlib.pyplot as pltdef function_2(x):return x[0]**2 + x[1]**2
# 或者 return np.sum(x**2)# 梯度
def numerical_gradient(f, x):h = 1e-4 # 0.0001grad = np.zeros_like(x) # 生成和形状相同的数组print(x.shape)print(x.size)for idx in range(x.size):tmp_val = x[idx]x[idx] = tmp_val + hfxh1 = f(x)x[idx] = tmp_val - hfxh2 = f(x)grad[idx] = (fxh1 - fxh2) / (2*h)x[idx] = tmp_val # 还原值return grad# 梯度下降
def gradient_descent(f, init_x, lr=0.01, step_num=100):x = init_xfor i in range(step_num):grad = numerical_gradient(f, x)x -= lr * gradreturn xinit_x = np.array([-3.0, 4.0])
d1 = gradient_descent(function_2, init_x, 0.1, 100)
print(d1) # [-6.11110793e-10 8.14814391e-10]
参数 f是要进行最优化的函数, init_x是初始值, lr是学习率learning
rate, step_num是梯度法的重复次数。 numerical_gradient(f,x)会求函数的
梯度,用该梯度乘以学习率得到的值进行更新操作,由step_num指定重复的
次数。
实验结果表明,学习率过大的话,会发散成一个很大的值;反过来,学
习率过小的话,基本上没怎么更新就结束了。也就是说,设定合适的学习率
是一个很重要的问题。
超参数
像学习率这样的参数称为超参数。这是一种和神经网络的参数(权重
和偏置)性质不同的参数。相对于神经网络的权重参数是通过训练
数据和学习算法自动获得的,学习率这样的超参数则是人工设定的。
一般来说,超参数需要尝试多个值,以便找到一种可以使学习顺利
进行的设定。
10.神经网络的梯度


