当前位置：首页 > news >正文

详解AVL树旋转操作实现

news 2025/10/14 13:53:42

一、AVL树概念

AVL树是最先发明的自平衡⼆叉查找树，AVL是⼀颗空树，或者具备下列性质的二叉搜索树：它的左右子树都是AVL树，且左右子树的高度差的绝对值不超过1AVL树是⼀颗高度平衡搜索⼆叉树，通过控制高度差去控制平衡。

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis是两个前苏联的科学家，他们在1962年的论文《An algorithm for the organization of information》中发表了它。
AVL树实现这里我们引入⼀个平衡因子(balance factor)的概念，每个结点都有⼀个平衡因子，任何结点的平衡因子等于右子树的高度减去左子树的高度，也就是说任何结点的平衡因子等于0/1/-1，AVL树并不是必须要平衡因子，但是有了平衡因子可以更方便我们去进行观察和控制树是否平衡，就像⼀个风向标⼀样。
思考⼀下为什么AVL树是高度平衡搜索⼆叉树，要求高度差不超过1，而不是高度差是0呢？0不是更好的平衡吗？画画图分析我们发现，不是不想这样设计，而是有些情况是做不到高度差是0的。⽐如⼀棵树是2个结点，4个结点等情况下，高度差最好就是1，无法做到高度差是0
AVL树整体结点数量和分布和完全二叉树类似，高度可以控制在，那么增删查改的效率也可以控制在，相比二叉搜索树有了本质的提升

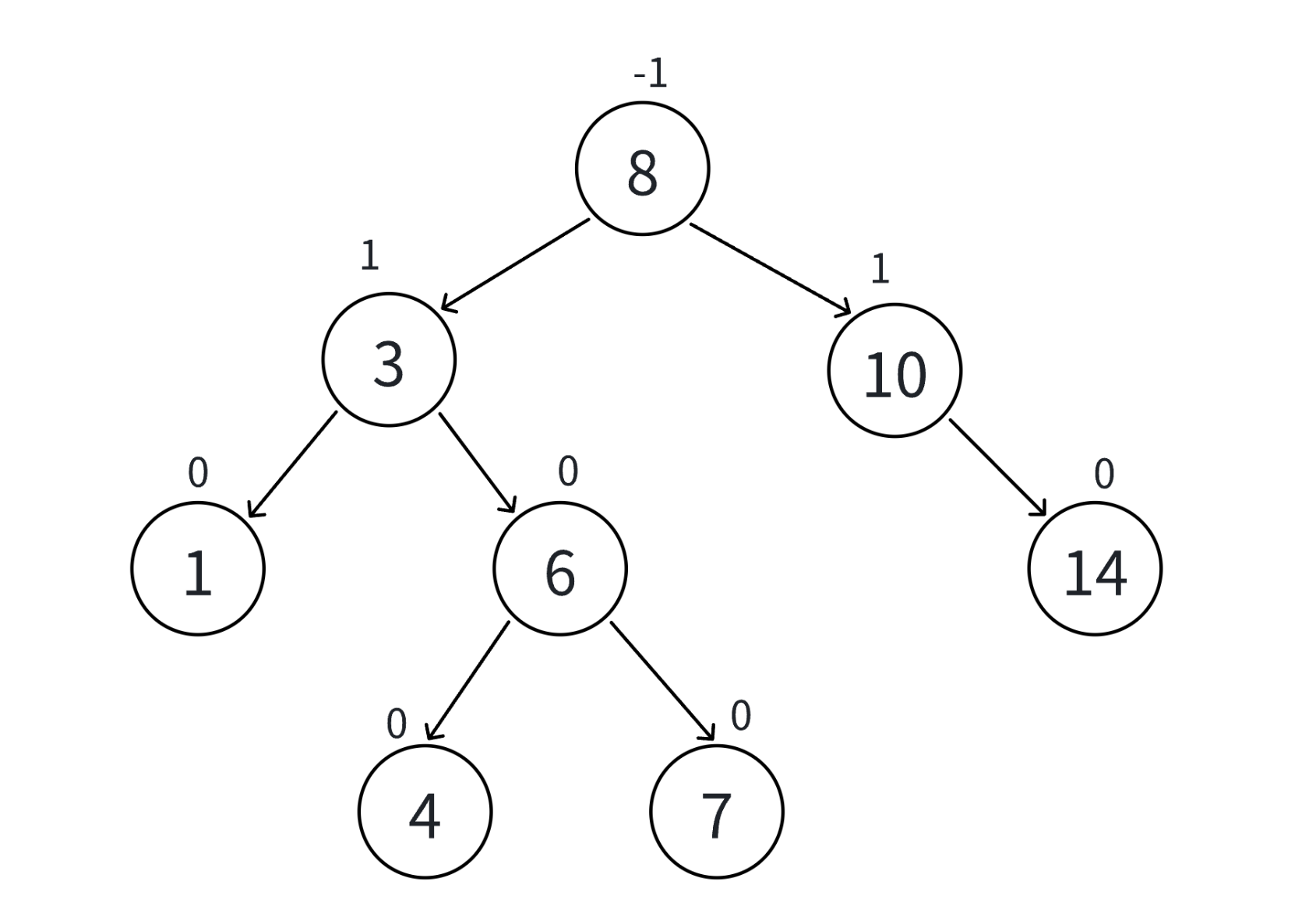
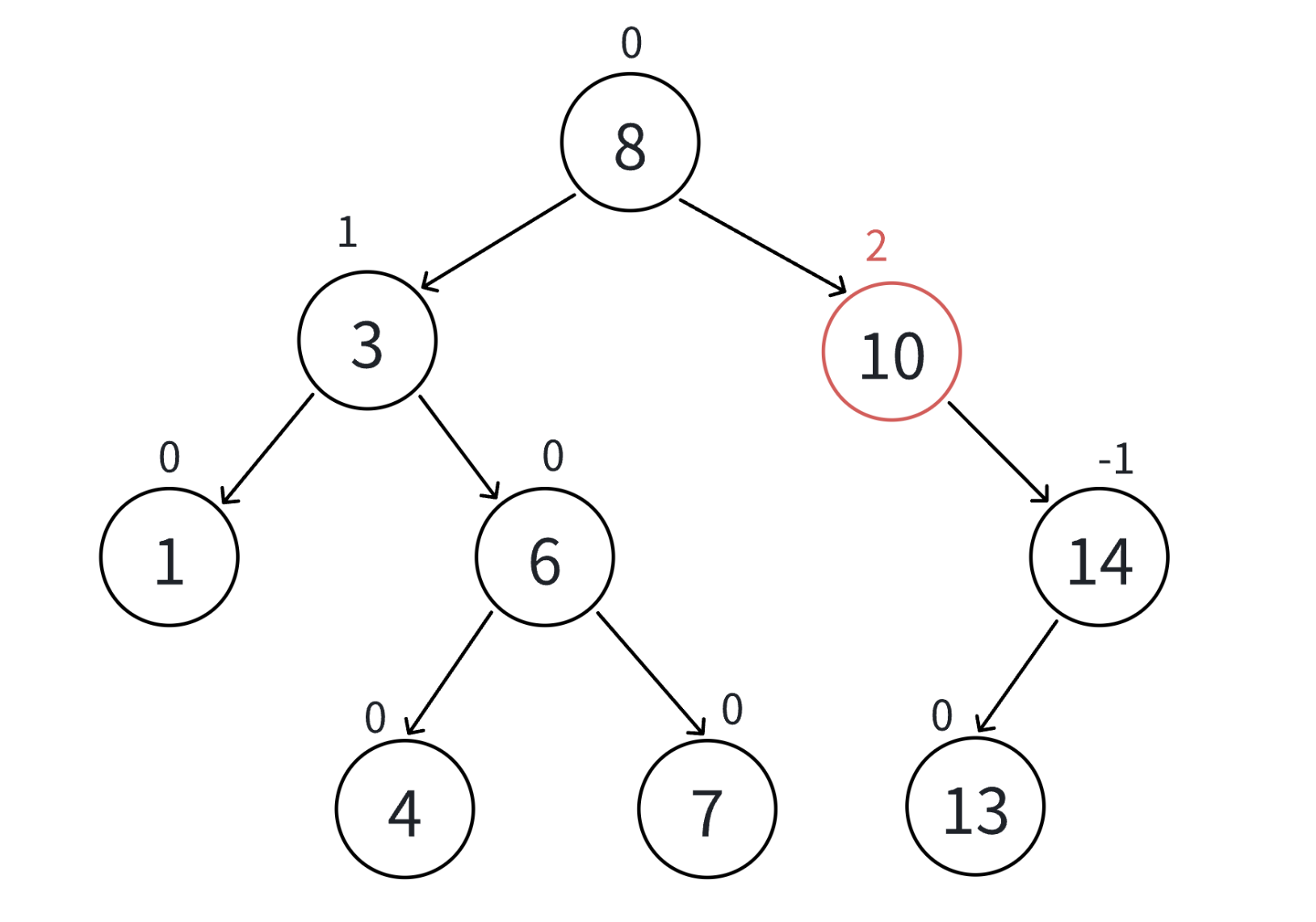
在这里插入图片描述

创建一个树节点和一个树的结构如下：(需要parent指针，后续更新平衡因子可以看到)

template<class K, class V>
struct AVLTreeNode
{pair<K, V> _kv;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;AVLTreeNode<K, V>* _parent;int _bf;AVLTreeNode(const pair<K, V>& kv):_kv(kv),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}
};

旋转的原则

保持搜索树的规则
让旋转的树从不满足变平衡，其次降低旋转树的高度旋转总共分为四种，左单旋/右单旋/左右双旋/右左双旋。说明：下面的图中，有些结点我们给的是具体值，如10和5等结点，这里是为了方便讲解，实际中是什么值都可以，只要大小关系符合搜索树的性质即可。

在旋转操作实现前先完成插入操作，其实和前面写的二叉平衡树大差不差：

	bool Insert(const pair<K, V>& kv){//查找对应位置，这里跟二叉平衡树一样if (_root == nullptr){_root = new Node(kv);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}//插入节点cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}//这里跟二叉平衡树不一样的地方，这里要记录parent方便后续调整位置cur->_parent = parent;//更新平衡因子while (parent){if (cur == parent->left) parent->_bf--;else parent->_bf++;}if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){//往上更新cur = parent;parent = parent->parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转if (parent->_bf == -2 || parent->_bf == -1){//右单旋RotateR(node * parent);}if (parent->_bf == 2 || parent->_bf == 1){//左单旋RotateL(node * parent);}if (parent->_bf == -2 || parent->_bf == 1){//右左双旋RotateLR(node * parent);}if (parent->_bf == 2 || parent->_bf == -1){//左右双旋RotateRL(node* parent);}break;}else{assert(false);}}

右单旋

1、在a子树中插入⼀个新结点，导致a子树的高度从h变成h+1，不断向上更新平衡因子，导致10的平衡因子从-1变成-2，10为根的树左右高度差超过1，违反平衡规则。10为根的树左边太高了，需要往右边旋转，控制两棵树的平衡。
2、旋转核心步骤，因为5 < b子树的值 < 10，将b变成10的左子树，10变成5的右子树，5变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的高度恢复到了插入之前的h+2，符合旋转原则。如果插入之前10整棵树的⼀个局部子树，旋转后不会再影响上⼀层，插入结束了。
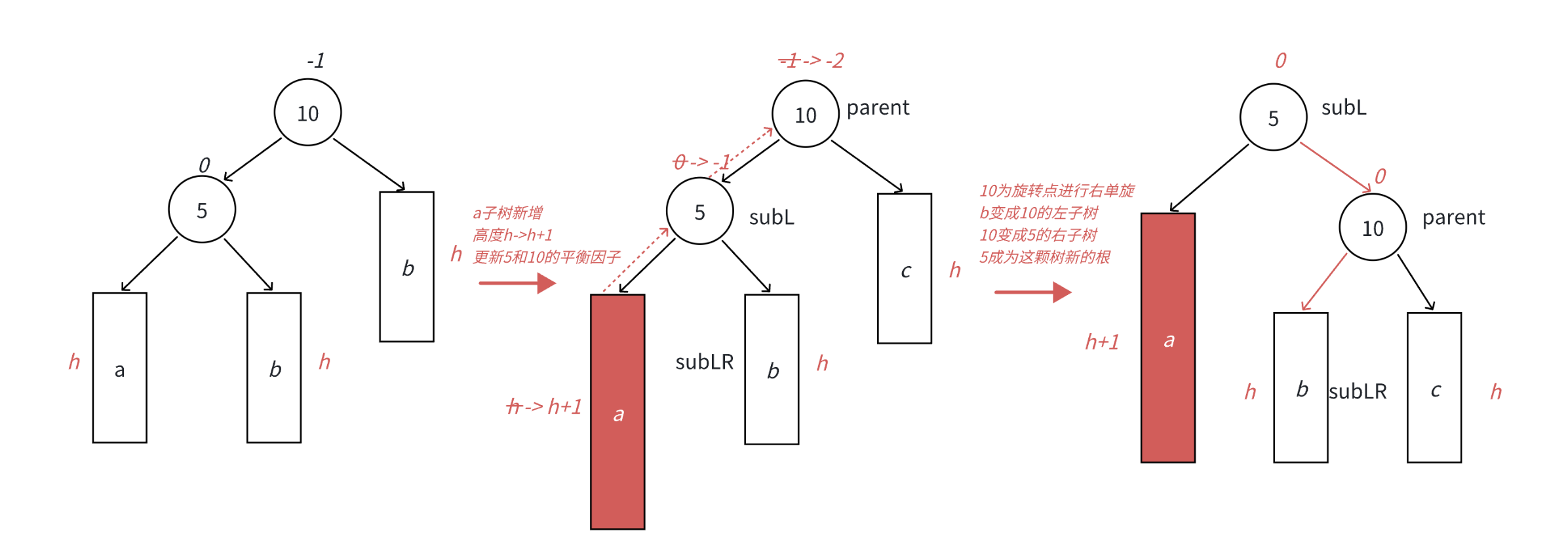
在这里插入图片描述
具体实现：

void RotateR(node* parent)
{node* subl = parent->_left;node* sublr = subl->_right;//旋转parent->_left = sublr;if (sublr) sublr->_parent = parent;//记录parentparentnode* parentparent = parent->_parent;subl->_right = parent;parent->_parent = subl;//我们不知道parentparent是根节点还是空所以判断if (parentparent == nullptr){_root = subl;subl->_parent = nullptr;}else{if (parentparent->_left == parent) parentparent->_left = subl;else parentparent->_right = subl;//记录parent方便调整subl->_parent = parentparent;}//更改平衡因子parent->_bf = subl->_bf = 0;
}

左单旋

1、在a子树中插入一个新结点，导致a子树的高度从h变成h+1，不断向上更新平衡因子，导致10的平衡因子从1变成2，10为根的树左右高度差超过1，违反平衡规则。10为根的树右边太高了，需要往左边旋转，控制两棵树的平衡。
2、旋转核心步骤，因为10 < b子树的值 < 15，将b变成10的右子树，10变成15的左子树，15变成这棵树新的根，符合搜索树的规则，控制了平衡，同时这棵的高度恢复到了插入之前的h+2，符合旋转原则。如果插入之前10整棵树的⼀个局部子树，旋转后不会再影响上⼀层，插入结束了。
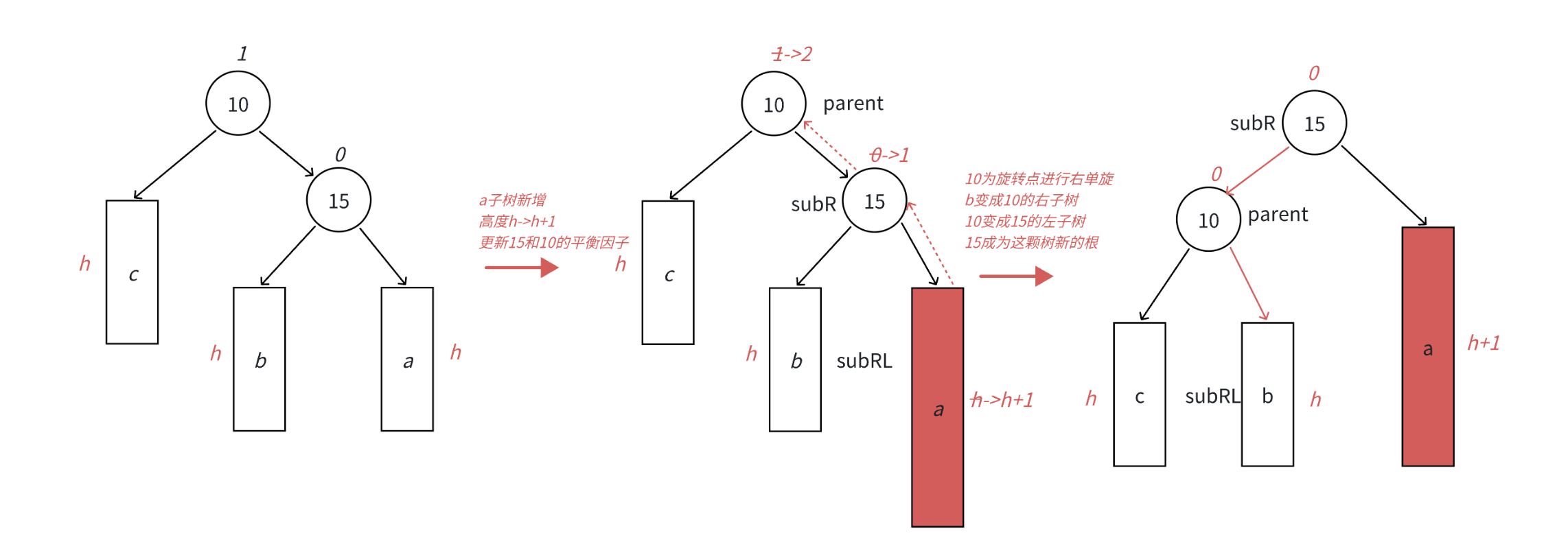
在这里插入图片描述

代码实现：

void RotateL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;Node* parentParent = parent->_parent;subR->_left = parent;parent->_parent = subR;if (parentParent == nullptr){_root = subR;subR->_parent = nullptr;}else{if (parent == parentParent->_left){parentParent->_left = subR;}else{parentParent->_right = subR;}subR->_parent = parentParent;}parent->_bf = subR->_bf = 0;
}

左右双旋

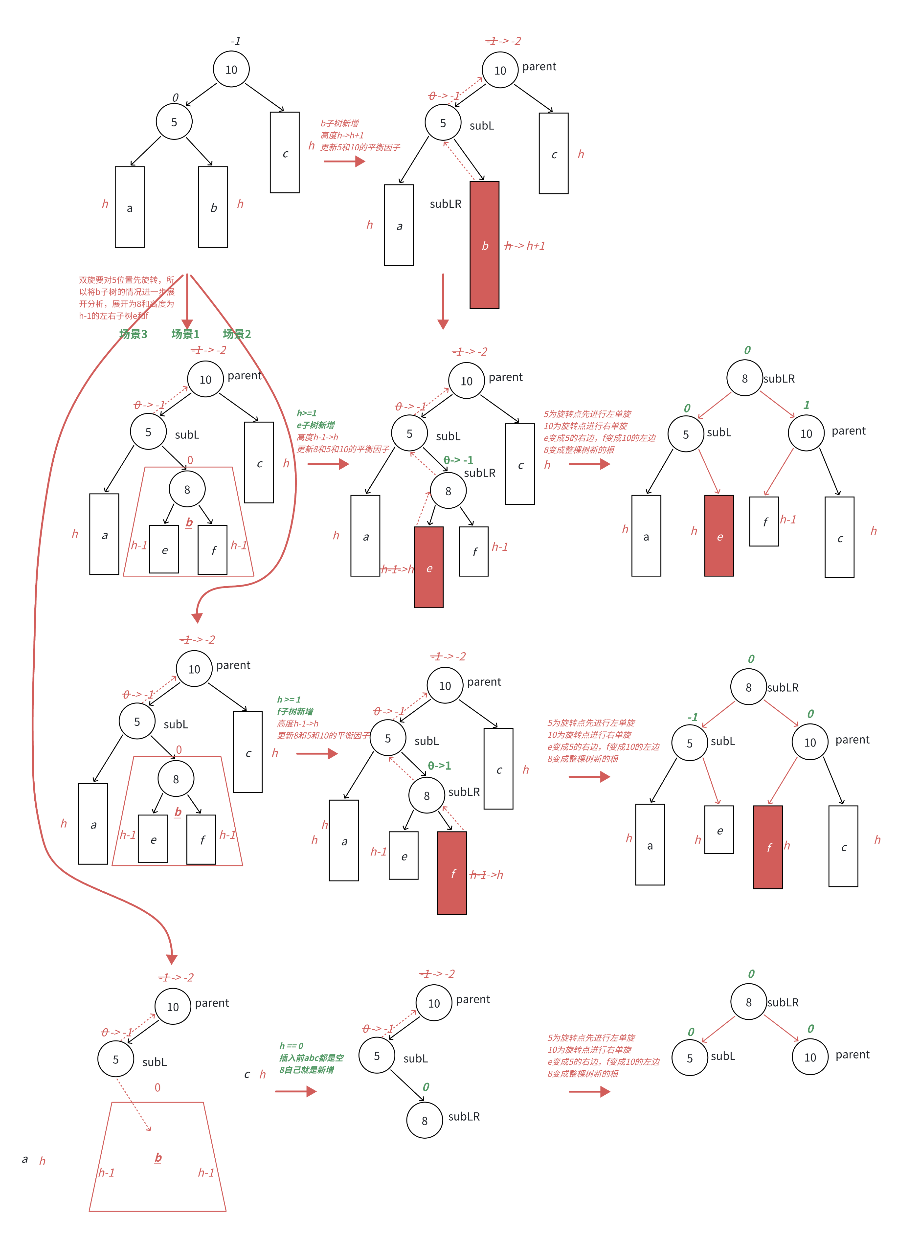
在这里插入图片描述

场景1：h >= 1时，新增结点插入在e子树，e子树高度从h-1并为h并不断更新8->5->10平衡因子，引发旋转，其中8的平衡因子为-1，旋转后8和5平衡因子为0，10平衡因子为1。
场景2：h >= 1时，新增结点插入在f子树，f子树高度从h-1变为h并不断更新8->5->10平衡因子，引发旋转，其中8的平衡因子为1，旋转后8和10平衡因子为0，5平衡因子为-1。
场景3：h == 0时，a/b/c都是空树，b自己就是⼀个新增结点，不断更新5->10平衡因子，引发旋转，其中8的平衡因子为0，旋转后8和10和5平衡因子均为0。

代码实现（这里直接复用上面左右单旋的代码就能更加简洁）

void RotateLR(node* parent)
{node* subl = parent->_left;node* sublr = subl->_right;int bf = sublr->_bf;//复用RotateL(parent->_left);RotateR(parent);//更新平衡因子if (bf == 0){sublr->_bf = 0;subl->_bf = 0;parent->_bf = 0;}else if (bf == 1){sublr->_bf = 0;subl->_bf = -1;parent->_bf = 0;}else if (bf == -1){sublr->_bf = 0;subl->_bf = 0;parent->_bf = 1;}else{assert(false);}
}

右左双旋

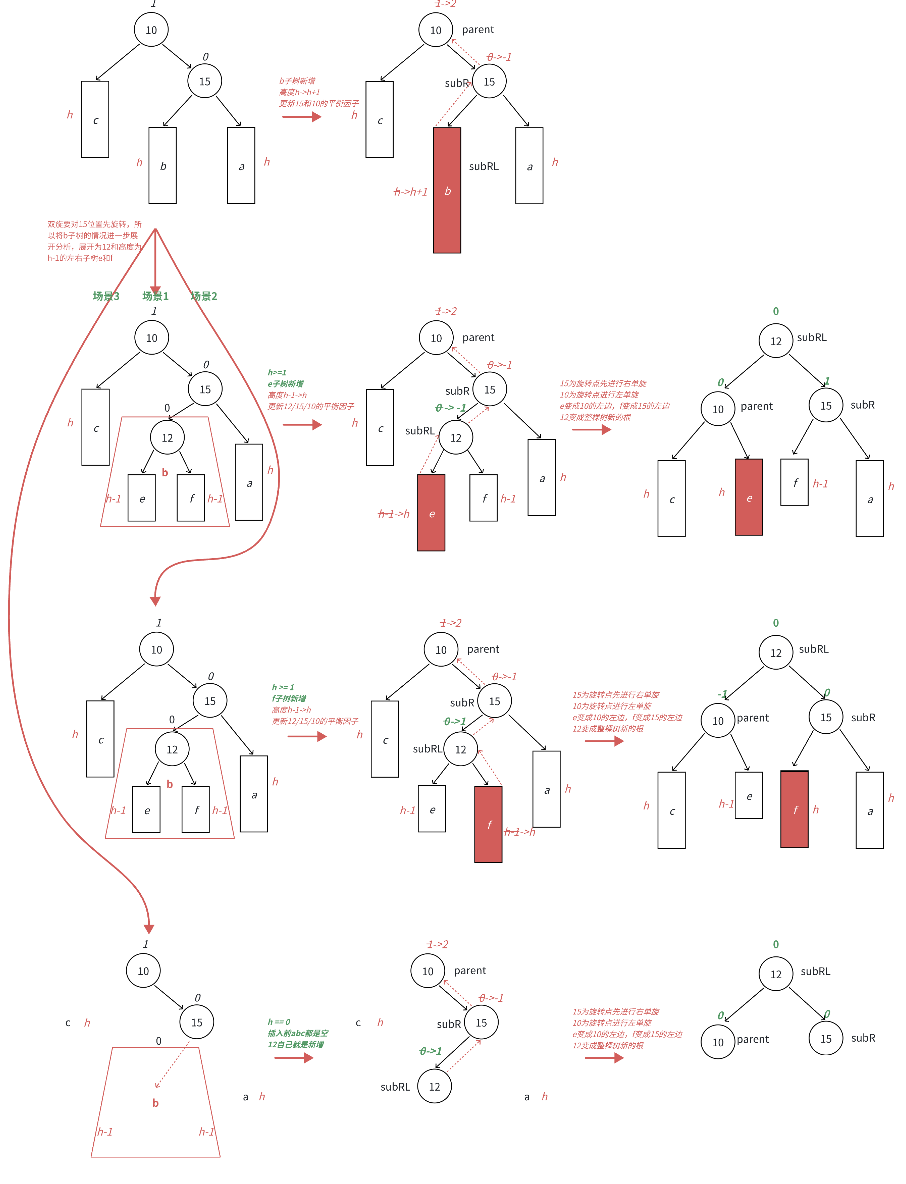
在这里插入图片描述

场景1：h >= 1时，新增结点插入在e子树，e子树高度从h-1变为h并不断更新12->15->10平衡因子，引发旋转，其中12的平衡因子为-1，旋转后10和12平衡因子为0，15平衡因子为1。
场景2：h >= 1时，新增结点插入在f子树，f子树高度从h-1变为h并不断更新12->15->10平衡因子，引发旋转，其中12的平衡因子为1，旋转后15和12平衡因子为0，10平衡因子为-1。
场景3：h == 0时，a/b/c都是空树，b自己就是⼀个新增结点，不断更新15->10平衡因子，引发旋转，其中12的平衡因子为0，旋转后10和12和15平衡因子均为0。

代码实现：

void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(parent->_right);RotateL(parent);if (bf == 0){subR->_bf = 0;subRL->_bf = 0;parent->_bf = 0;}else if (bf == 1){subR->_bf = 0;subRL->_bf = 0;parent->_bf = -1;}else if (bf == -1){subR->_bf = 1;subRL->_bf = 0;parent->_bf = 0;}else{assert(false);}
}