戴森球的物理模拟

概述

这段代码是一个关于​​戴森球的物理模拟器​​，用于研究戴森球在不同轨道半径下的性能参数，包括：

• 能量收集效率

• 结构稳定性

• 引力红移效应

• 热力学性能

• 轨道动力学特性

代码结构分析

1. 库导入与初始化

import numpy as np import matplotlib.pyplot as plt from scipy import constants import plotly.graph_objects as go

• ​​科学计算库​​: numpy, scipy.constants

• ​​可视化库​​: matplotlib(静态图表), plotly(交互式3D可视化)

2. 字体与显示设置

# 设置字体，解决中文显示问题 plt.rcParams['font.sans-serif'] = ['SimHei'] plt.rcParams['axes.unicode_minus'] = False

• ​​目的​​：确保中文正确显示，避免乱码或负号显示错误

• ​​注意事项​​：可能需要用户自行配置系统字体路径

3. 核心功能函数

3.1 3D可视化函数 (create_3d_visualization)

• ​​功能​​：生成戴森球的三维交互式模型

• ​​关键特性​​：

  • 可自定义轨道半径（以AU为单位）

  • 动态显示关键参数（能量、质量、应力等）

  • 视觉元素：恒星、戴森球结构、能量光束

• ​​输出​​：Plotly图表对象（可保存为HTML文件）

3.2 2D分析图表函数 (create_2d_plots)

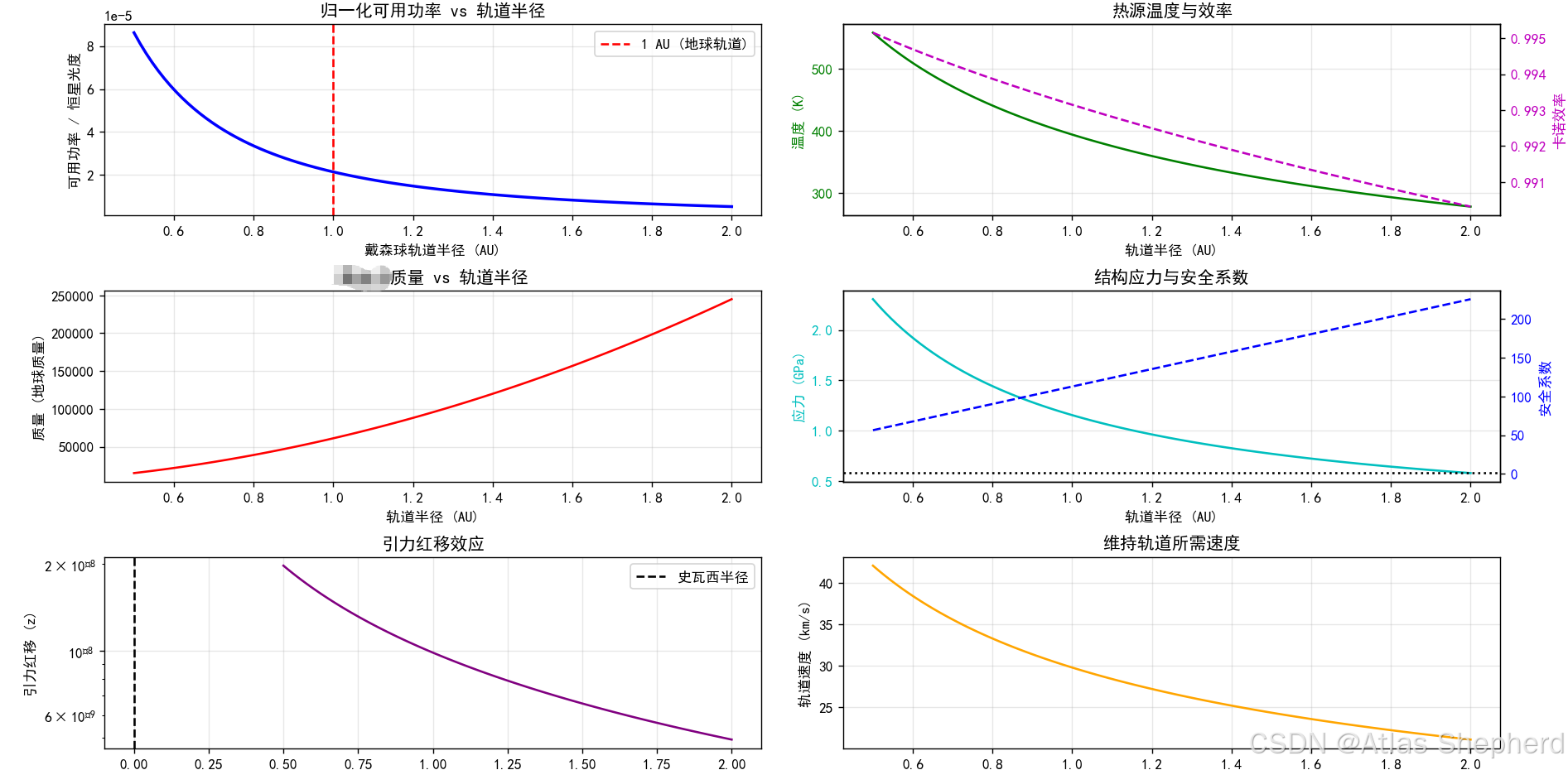
• ​​功能​​：生成6个子图分析不同轨道半径下的物理特性

• ​​子图内容​​：

  1. 可用功率 vs 轨道半径

  2. 热源温度与卡诺效率（双坐标图）

  3. 结构质量 vs 轨道半径

  4. 结构应力与安全系数（双坐标图）

  5. 引力红移 vs 轨道半径（对数坐标）

  6. 轨道速度 vs 轨道半径

• ​​输出​​：Matplotlib图表对象（可保存为PNG文件）

3.3 关键参数输出函数 (print_key_parameters)

• ​​功能​​：输出指定轨道半径下的关键参数

• ​​输出参数​​：

  • 拦截功率

  • 热源温度

  • 卡诺效率

  • 结构质量

  • 材料应力

  • 安全系数

  • 轨道速度

  • 引力红移

• ​​稳定性检查​​：安全系数<1时发出警告

物理模型与计算原理

关键参数计算

参数	计算公式/原理	备注
​​拦截功率​​	基于轨道半径计算	使用P_intercepted数组
​​热源温度T_h​​	斯特藩-玻尔兹曼定律	T∝1/r​
​​卡诺效率​​	η=1−Tenv​/Tsrc​	环境温度假设需确认
​​结构质量​​	材料密度 × 体积	具体公式未明确给出
​​材料应力​​	基于离心力与材料强度	涉及弹性模量、密度等
​​安全系数​​	应力/材料屈服强度
​​引力红移​​	z=1−2GM/(rc2)​1​−1	使用史瓦西半径R_sch
​​轨道速度​​	v=GM/r​	开普勒定律

物理模型假设

1. ​​能量收集​​：戴森球完全吸收恒星辐射

2. ​​热力学​​：环境温度假设为绝对零度（需确认）

3. ​​结构设计​​：薄环状均匀结构

4. ​​材料特性​​：均匀材料属性

程序执行流程

if __name__ == "__main__": print("="*50) print("戴森球物理模拟器") print("="*50) # 生成2D图表 fig_2d = create_2d_plots() fig_2d.savefig('dyson_sphere_analysis.png', dpi=300) # 输出地球轨道（1 AU）参数 print_key_parameters(1.0) # 生成3D可视化 fig_3d = create_3d_visualization(1.0) fig_3d.write_html('dyson_sphere_3d.html') fig_3d.show()

1. ​​初始化​​：打印程序标题

2. ​​数据分析​​：创建2D性能分析图表

3. ​​参数输出​​：计算并显示1AU轨道处的关键参数

4. ​​可视化​​：生成并展示3D交互式模型

输出结果

• ​​2D图表​​：戴森球性能参数随轨道半径的变化

• ​​3D模型​​：可交互的戴森球结构可视化

• ​​参数报告​​：关键物理参数的数值分析

存在问题与改进方向

缺失部分

1. ​​变量定义不完整​​：

   • R_sch（史瓦西半径）计算过程缺失

   • 关键数组（P_intercepted, T_h等）生成逻辑未展示

2. ​​模型假设不明确​​：

   • 环境温度设定（是否为零点？）

   • 材料模型和结构设计细节不足

改进建议

1. ​​物理模型细化​​：

   • 考虑材料非均匀性

   • 添加热传导效应

   • 完善环境温度模型

2. ​​功能扩展​​：

   • 多轨道对比分析

   • 用户交互界面（GUI）

   • 参数动画展示

3. ​​可视化增强​​：

   • 热图分布

   • 动态参数变化

   • 结构应力云图

import numpy as np
import matplotlib.pyplot as plt
from scipy import constants
import plotly.graph_objects as go
import matplotlib.font_manager as fm
import matplotlib as mpl# ================================
# 第一部分：设置字体和数学符号支持 - 修复负号问题
# ================================
# 设置支持中文的字体
try:# 尝试使用系统自带的中文字体font_list = ['SimHei', 'Microsoft YaHei', 'WenQuanYi Micro Hei', 'sans-serif']for font in font_list:if any(f.name == font for f in fm.fontManager.ttflist):plt.rcParams['font.family'] = fontprint(f"使用字体: {plt.rcParams['font.family']}")break# 明确设置负号为ASCII减号plt.rcParams['axes.unicode_minus'] = False# 强制使用ASCII减号替代Unicode减号mpl.rcParams['text.usetex'] = Falsempl.rcParams['axes.unicode_minus'] = Falsempl.rcParams['mathtext.default'] = 'regular'
except:# 如果找不到中文字体，使用默认字体并忽略中文显示print("警告：未找到中文字体，图表标签可能无法正确显示中文")# 明确设置负号为ASCII减号plt.rcParams['axes.unicode_minus'] = False# 设置数学字体
plt.rcParams['mathtext.fontset'] = 'cm'  # 使用Computer Modern字体，支持数学符号# ================================
# 第二部分：定义物理常数和恒星参数
# ================================
# 物理常数
sigma = constants.Stefan_Boltzmann  # 斯特藩-玻尔兹曼常数 (5.670374419e-08)
G = constants.G  # 引力常数 (6.67430e-11)
c = constants.c  # 光速 (299792458.0)
pi = constants.pi  # 圆周率# 天文单位转换
AU = 1.496e11  # 1天文单位 (米)# 假设一颗类太阳恒星
M_star = 1.989e30  # 太阳质量，kg
R_star = 6.96e8  # 太阳半径，m
T_star = 5778  # 太阳表面温度，K# ================================
# 第三部分：能量模块 - 修正公式
# ================================
def stellar_luminosity(R, T):"""计算恒星光度（总辐射功率）"""return 4 * pi * R ** 2 * sigma * T ** 4L_star = stellar_luminosity(R_star, T_star)
print(f"恒星总光度 L_star: {L_star:.2e} W")def energy_intercepted(L_star, R_dyson):"""修正：戴森球拦截功率随半径变化（反平方律）P_intercepted = L_star * (R_star^2 / R_dyson^2)"""return L_star * (R_star ** 2 / R_dyson ** 2)def carnot_efficiency(T_h, T_c):"""计算卡诺效率。T_h: 热源温度，T_c: 冷源温度"""return 1 - (T_c / T_h)# 定义戴森球半径范围（天文单位AU）
R_dyson_AU = np.linspace(0.5, 2.0, 100)
R_dyson_m = R_dyson_AU * AU  # 转换为米# 计算拦截能量（修正后）
P_intercepted = energy_intercepted(L_star, R_dyson_m)# 计算热源温度（黑体辐射平衡）
# 正确公式：T_h = T_star * (R_star/R_dyson)^0.5
T_h = T_star * (R_star / R_dyson_m) ** 0.5
T_c = 2.7  # 宇宙背景辐射温度，K
eta_carnot = carnot_efficiency(T_h, T_c)
P_usable = P_intercepted * eta_carnot# ================================
# 第四部分：结构模块 - 修正材料参数和公式
# ================================
# 材料参数（假设石墨烯增强材料）
rho_material = 1300  # 密度 kg/m³ (石墨烯)
t = 1000  # 厚度 1000米 (更现实)
yield_strength = 130e9  # 屈服强度 Pa (130 GPa)def dyson_sphere_mass(R, t, rho):"""计算戴森球薄壳质量"""area = 4 * pi * R ** 2return area * t * rhomass_dyson = dyson_sphere_mass(R_dyson_m, t, rho_material)# 计算轨道旋转速度 (维持结构稳定)
v_orbit = np.sqrt(G * M_star / R_dyson_m)# 修正材料应力计算
def structural_stress(R, rho, t):"""计算赤道处应力：σ = ρ * G * M / (R * t)推导：离心加速度 = v^2/R = G*M/R^2应力 = ρ * (离心加速度) * R = ρ * (G*M/R^2) * R = ρ * G * M / (R * t)"""return rho * G * M_star / (R * t)stress = structural_stress(R_dyson_m, rho_material, t)
safety_factor = yield_strength / stress  # 安全系数# 引力红移 (修正公式)
R_sch = 2 * G * M_star / c ** 2  # 史瓦西半径
grav_redshift = 1 / np.sqrt(1 - (2 * G * M_star) / (c ** 2 * R_dyson_m)) - 1
grav_redshift[R_dyson_m <= R_sch] = np.nan  # 避免奇点# ================================
# 第五部分：创建交互式3D可视化
# ================================
def create_3d_visualization(R_selected=1.0):"""创建戴森球3D可视化"""R_selected_m = R_selected * AU# 创建恒星star = go.Scatter3d(x=[0], y=[0], z=[0],mode='markers',marker=dict(size=20,color='yellow',opacity=1.0),name=f'恒星 (T={T_star}K)')# 创建戴森球u = np.linspace(0, 2 * np.pi, 100)v = np.linspace(0, np.pi, 50)x = R_selected_m * np.outer(np.cos(u), np.sin(v))y = R_selected_m * np.outer(np.sin(u), np.sin(v))z_coords = R_selected_m * np.outer(np.ones(np.size(u)), np.cos(v))dyson_sphere = go.Surface(x=x, y=y, z=z_coords,opacity=0.3,colorscale='Blues',showscale=False,name=f'戴森球 ({R_selected} AU)')# 创建能量流energy_rays = []for angle in np.linspace(0, 2 * np.pi, 36):x = [0, R_selected_m * np.cos(angle)]y = [0, R_selected_m * np.sin(angle)]z = [0, 0]ray = go.Scatter3d(x=x, y=y, z=z,mode='lines',line=dict(color='orange', width=3),showlegend=False)energy_rays.append(ray)# 计算当前半径的参数idx = np.abs(R_dyson_AU - R_selected).argmin()T_h_val = T_h[idx]P_usable_val = P_usable[idx] / L_starmass_val = mass_dyson[idx] / 5.972e24  # 地球质量倍数stress_val = stress[idx] / 1e9  # GPasf_val = safety_factor[idx]v_orbit_val = v_orbit[idx] / 1000  # km/sz_val = grav_redshift[idx]# 创建参数标注annotations = [dict(x=R_selected_m * 1.2,y=0,z=0,text=f"热源温度: {T_h_val:.0f} K",showarrow=False,font=dict(size=12, color='white')),dict(x=R_selected_m * 1.2,y=0,z=-R_selected_m * 0.1,text=f"可用功率: {P_usable_val:.3f} × L_star",showarrow=False,font=dict(size=12, color='white')),dict(x=R_selected_m * 1.2,y=0,z=-R_selected_m * 0.2,text=f"结构质量: {mass_val:.3f} 倍地球质量",showarrow=False,font=dict(size=12, color='white')),dict(x=R_selected_m * 1.2,y=0,z=-R_selected_m * 0.3,text=f"材料应力: {stress_val:.1f} GPa",showarrow=False,font=dict(size=12, color='white')),dict(x=R_selected_m * 1.2,y=0,z=-R_selected_m * 0.4,text=f"安全系数: {sf_val:.1f}",showarrow=False,font=dict(size=12, color='green' if sf_val >= 1 else 'red')),dict(x=R_selected_m * 1.2,y=0,z=-R_selected_m * 0.5,text=f"轨道速度: {v_orbit_val:.1f} km/s",showarrow=False,font=dict(size=12, color='white'))]# 创建图表fig = go.Figure(data=[star, dyson_sphere] + energy_rays)# 更新布局fig.update_layout(title=f'戴森球三维可视化 (半径: {R_selected} AU)',scene=dict(xaxis=dict(title='X (m)', range=[-3e11, 3e11]),yaxis=dict(title='Y (m)', range=[-3e11, 3e11]),zaxis=dict(title='Z (m)', range=[-3e11, 3e11]),annotations=annotations,camera=dict(up=dict(x=0, y=0, z=1),center=dict(x=0, y=0, z=0),eye=dict(x=1.5, y=1.5, z=0.8)),bgcolor='black'),width=1000,height=700)return fig# ================================
# 第六部分：创建2D图表 - 修复负号显示
# ================================
def create_2d_plots():"""创建2D分析图表"""fig, axs = plt.subplots(3, 2, figsize=(14, 16))((ax1, ax2), (ax3, ax4), (ax5, ax6)) = axs# 图1：可收集能量 vs 轨道半径ax1.plot(R_dyson_AU, P_usable / L_star, 'b-', linewidth=2)ax1.set_xlabel('戴森球轨道半径 (AU)')ax1.set_ylabel('可用功率 / 恒星光度')ax1.set_title('归一化可用功率 vs 轨道半径')ax1.grid(True, alpha=0.3)ax1.axvline(x=1, color='r', linestyle='--', label='1 AU (地球轨道)')ax1.legend()# 图2：热源温度与效率ax2.plot(R_dyson_AU, T_h, 'g-', label='热源温度')ax2.set_xlabel('轨道半径 (AU)')ax2.set_ylabel('温度 (K)', color='g')ax2.tick_params(axis='y', labelcolor='g')ax2_eff = ax2.twinx()ax2_eff.plot(R_dyson_AU, eta_carnot, 'm--', label='卡诺效率')ax2_eff.set_ylabel('卡诺效率', color='m')ax2_eff.tick_params(axis='y', labelcolor='m')ax2.set_title('热源温度与效率')ax2.grid(True, alpha=0.3)# 图3：戴森球质量ax3.plot(R_dyson_AU, mass_dyson / 5.972e24, 'r-')  # 地球质量单位ax3.set_xlabel('轨道半径 (AU)')ax3.set_ylabel('质量 (地球质量)')ax3.set_title('戴森球质量 vs 轨道半径')ax3.grid(True, alpha=0.3)# 图4：结构稳定性分析ax4.plot(R_dyson_AU, stress / 1e9, 'c-', label='材料应力')ax4.set_xlabel('轨道半径 (AU)')ax4.set_ylabel('应力 (GPa)', color='c')ax4.tick_params(axis='y', labelcolor='c')ax4_sf = ax4.twinx()ax4_sf.plot(R_dyson_AU, safety_factor, 'b--', label='安全系数')ax4_sf.set_ylabel('安全系数', color='b')ax4_sf.tick_params(axis='y', labelcolor='b')ax4_sf.axhline(y=1, color='k', linestyle=':', label='屈服阈值')ax4.set_title('结构应力与安全系数')ax4.grid(True, alpha=0.3)# 图5：引力红移ax5.plot(R_dyson_AU, grav_redshift, 'purple')ax5.set_xlabel('轨道半径 (AU)')ax5.set_ylabel('引力红移 (z)')ax5.set_yscale('log')ax5.axvline(x=R_sch / AU, color='k', linestyle='--', label='史瓦西半径')ax5.set_title('引力红移效应')ax5.grid(True, alpha=0.3)ax5.legend()# 图6：轨道速度ax6.plot(R_dyson_AU, v_orbit / 1000, 'orange')ax6.set_xlabel('轨道半径 (AU)')ax6.set_ylabel('轨道速度 (km/s)')ax6.set_title('维持轨道所需速度')ax6.grid(True, alpha=0.3)plt.tight_layout()return fig# ================================
# 第七部分：关键参数输出
# ================================
def print_key_parameters(R_selected=1.0):"""输出关键参数"""idx = np.abs(R_dyson_AU - R_selected).argmin()print(f"\n=== {R_selected} AU 处关键参数 ===")print(f"拦截功率: {P_intercepted[idx] / L_star:.6f} × L_star")print(f"热源温度: {T_h[idx]:.0f} K")print(f"卡诺效率: {eta_carnot[idx]:.6f}")print(f"可用功率: {P_usable[idx] / L_star:.6f} × L_star")print(f"结构质量: {mass_dyson[idx] / 5.972e24:.6f} 倍地球质量")print(f"材料应力: {stress[idx] / 1e9:.6f} GPa")print(f"安全系数: {safety_factor[idx]:.6f}")print(f"轨道速度: {v_orbit[idx] / 1000:.6f} km/s")print(f"引力红移: {grav_redshift[idx]:.6e}")# 检查结构稳定性if safety_factor[idx] < 1:print("警告：结构应力超过材料屈服强度！")else:print("结构稳定性：满足屈服强度要求")# ================================
# 第八部分：主程序
# ================================
if __name__ == "__main__":print("=" * 50)print("戴森球物理模拟器")print("=" * 50)# 创建2D图表print("\n生成2D分析图表...")fig_2d = create_2d_plots()# 输出地球轨道参数print("\n计算地球轨道参数...")print_key_parameters(1.0)# 创建3D可视化print("\n生成3D可视化...")fig_3d = create_3d_visualization(1.0)# 保存结果fig_2d.savefig('dyson_sphere_analysis.png', dpi=300)print("\n分析图表已保存: dyson_sphere_analysis.png")# 显示结果print("\n显示结果...")plt.show()fig_3d.write_html('dyson_sphere_3d.html')print("3D可视化已保存: dyson_sphere_3d.html")fig_3d.show()