codeforces round1057(div2)AB题解
1.Circle of Apple Trees(苹果树圈)

题意:有n个苹果,第i个苹果的美丽程度是bi,你去吃苹果,在每棵树前可以吃也可以不吃,前提是所吃的这个苹果的bi值必须大于上一个所吃的,而且这个个圈,可以循环,问最多可以吃多少个苹果
思路:求一个数组中不同元素的个数(由题意很容易想到美丽程度相同的苹果不能吃两次,而其他的苹果可以循环吃,可以每一轮都吃美丽程度最小的那个)
int main()
//{
// int t = 0;
// cin >> t;
// while (t--)
// {
// int n = 0;
// cin >> n;
// vector<int>v;
// for (int i = 0; i < n; i++)
// {
// int num;
// cin >> num;
// v.push_back(num); // 正确添加元素的方式
// }
// sort(v.begin(), v.end());
// int cnt = 1;
// for (int i = 0; i < n - 1; i++)
// {
// if (v[i] == v[i + 1])
// {
// continue;
// }
// else
// {
// cnt++;
// }
// }
// cout << cnt << "\n";
// }
// return 0;
//}2. Bitwise Reversion(比特翻转)

题意: 已知x,y,z,且他们是由abc分别按位与得到的,求是否存在这样的abc
思路:1.首先明确按位与&:两个比特位上同时为1才能得到1,否则为0;
2.可以先简单举个例子观察一下规律
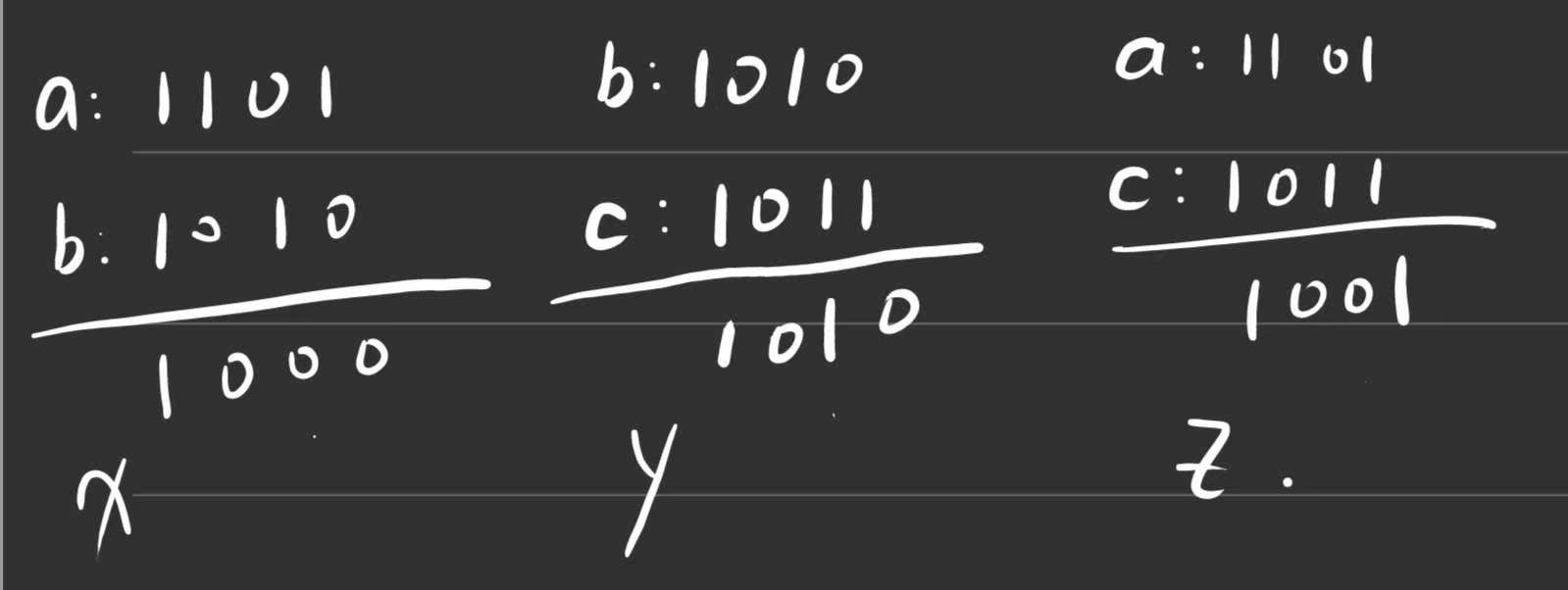
3.观察上图可以发现,x,y,z三者同一位上,要么是3个1,要么是1个1,绝对不能出现2个1的情况,由此即为核心逻辑。(a,b,c的同一位上如果有3个1,那么x,y,z的同一位上则有3个1;a,b,c的同一位上如果有2个1,那么x,y,z的同一位上则有1个1;a,b,c的同一位上如果有1个1,那么x,y,z的同一位上则有0个1)
int main()
{int x, y, z;cin >> x >> y >> z;for (int i = 0; i < 30; i++){if ((x >> i & 1) + (y >> i & 1) + (z >> i & 1) == 2)cout << "NO\n";}cout << "YES\n";return 0;
}3.Symmetrical Polygons(对称多边形)
 题意:有n 个小棒来拼对称凸多边形,问最大周长
题意:有n 个小棒来拼对称凸多边形,问最大周长
思路:1.初步:要想是对称,肯定有一个对称轴,我们往左右两边仍长度一样的小棒,剩下长度不一样的小棒,可以做边;所以先找出长度相同的小棒(两根为一组),看看剩余几条出现奇数的边长:
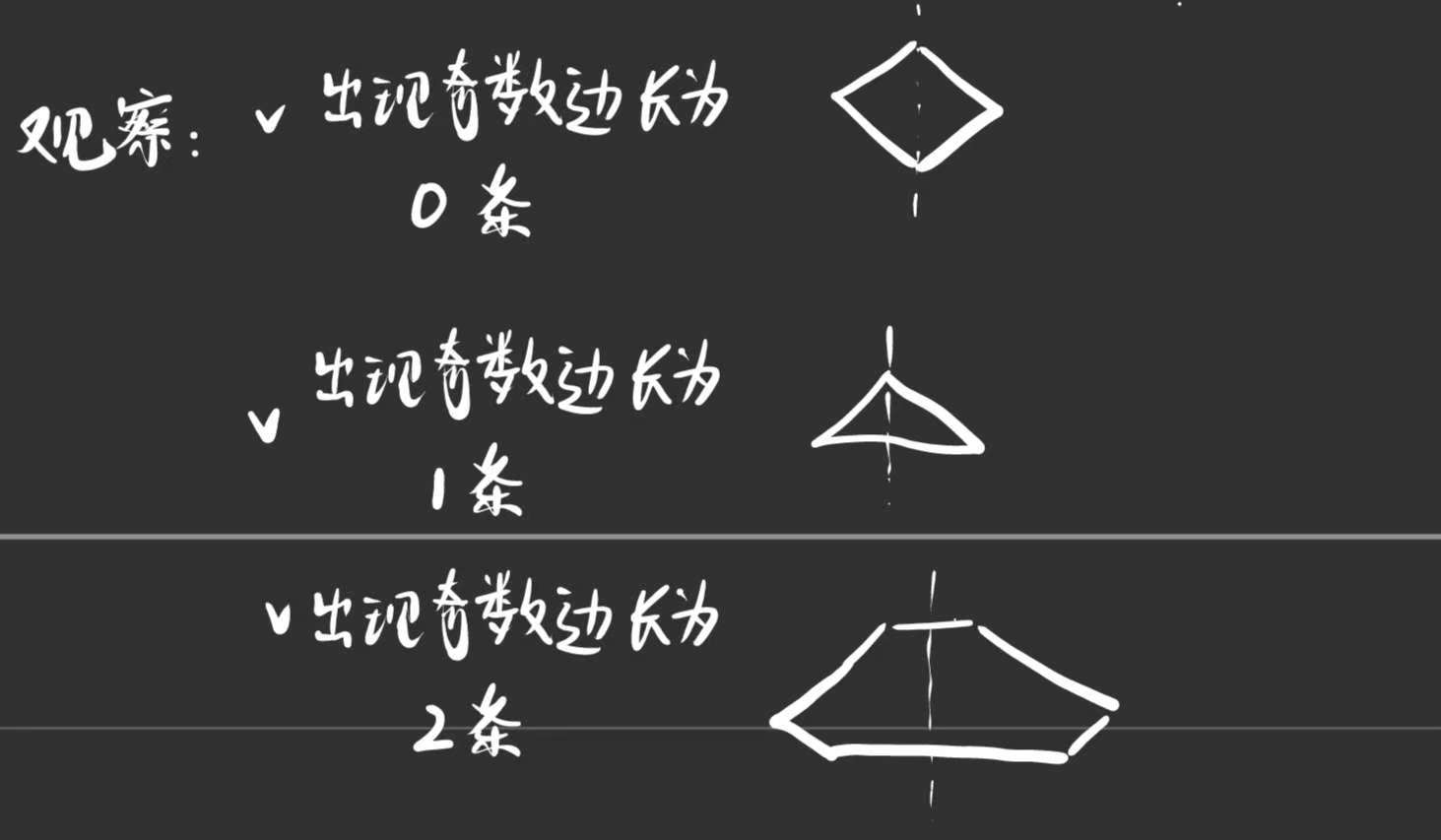
2.但是多边形的边需要 “首尾相连围成封闭图形”,如果某一条边太长,其余边的长度之和不足以 “包住” 这条长边,就无法形成封闭的多边形。
多边形存在的关键是:任意一条边的长度,都必须小于其余所有边的长度之和。
所以 最长边<其余所有边的和==>最长边<(所有边-最长边)==>最长边<所有边总和的一般
