LeetCode——双指针（进阶）

相关例题

快乐数

题目描述

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

提示：

• 1 <= n <= 231 - 1

题目分析

我们这里初看这个题目还是比较的新奇的，因为这个题目不是一看就可能会有思路的（除非你之前见过类似的题目），我们这里其实可以从题目中知道了一点实现的思路，因为题目中明确地指出了我们找不到1，那么我们最后就会出现循环的情况，这里我们也给出其中一种出现循环的情况：

2 -> 4 -> 16 ->37 ->58 -> 89 -> 145 -> 42 -> 20 -> 2 -> 4

我们这里可以看到我们这里出现了循环，其实我们这里实现的时候就只要关注于两件事情，第一个就是我们是不是算到1了，第二个就是我们这里是不是出现了循环的情况。

实现思路

其实这个题目很明显就是考察的我们的快慢指针的算法了，我们之前就讲过了，我们出现了循环的情况很可能就是要使用我们的快慢指针来实现了，这里我们也可以往这个方向上来写。于是我们这里就有了下面这个步骤：

1、定义一个快指针和一个慢指针，慢指针就是初始化成一开始的值，快指针就先做一次题目中要求的那么每个数的平方和的操作。

2、定义一个死循环，中间加上我们的判断（一个就是是不是算到了1，一个就是我们的慢指针是不是和快指针相等了（说明绕了圈之后相遇）），同时我们快指针走两步（计算两次），慢指针走一步（计算一次）即可，这个循环总有退出的时候。

实现代码

class Solution {
public:int slove(int t) {int sum = 0;while(t){int temp = t % 10;sum += temp * temp;t /= 10;}return sum;}bool isHappy(int n) {int a = slove(n);int b = slove(slove(n));while(true) {if(a == 1 || b == 1) {return true;}if(a == b){return false;}a = slove(a);b = slove(slove(b));}}
};

这个代码并不是我们的唯一写法，官方给出了哈希集合检测循环和纯数学找规律的写法（感觉自己不可能想到）。

盛最多水的容器

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

示例 1：

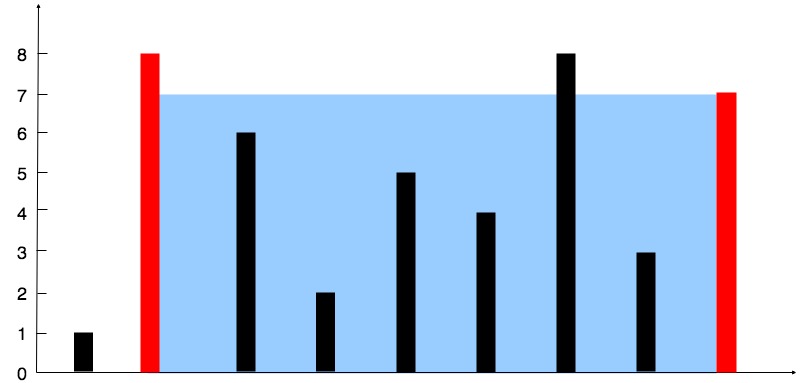
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

题目分析

其实这个题目也是一个考察双指针的题目，但是我当时写的时候死活想不到是怎么用的（QWQ），但是我们还是可以分析到一些东西的，我们首先要知道的是跟据木桶效应，我们的容量是根据矮的那个来计算的。

实现思路

我们这里的实现其实是有贪心的成分在的，我们可以极端的想，底最长的时候是容量最多的，那么什么时候可以改变我们的容量的最大值呢，那就只能左边或是右边往里面移动的时候了，这个时候就有了我们要贪心的地方了，分了两种情况：

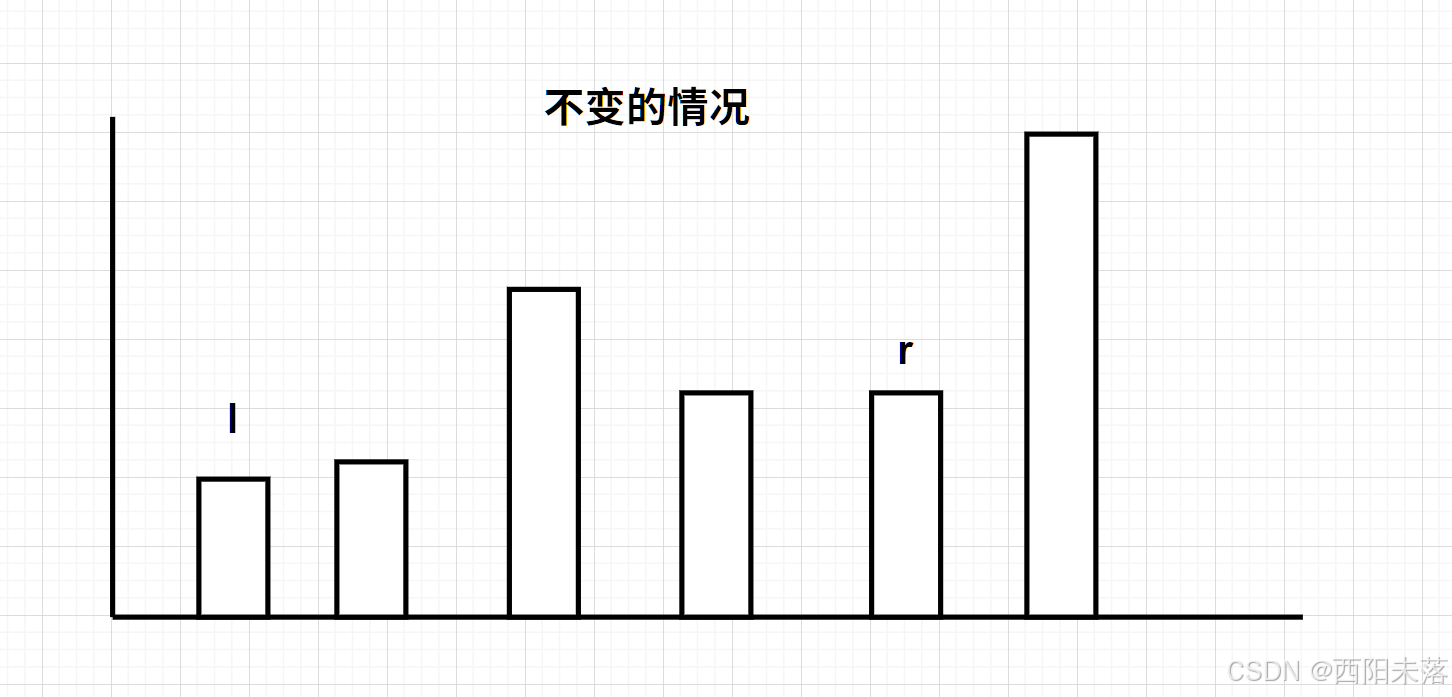
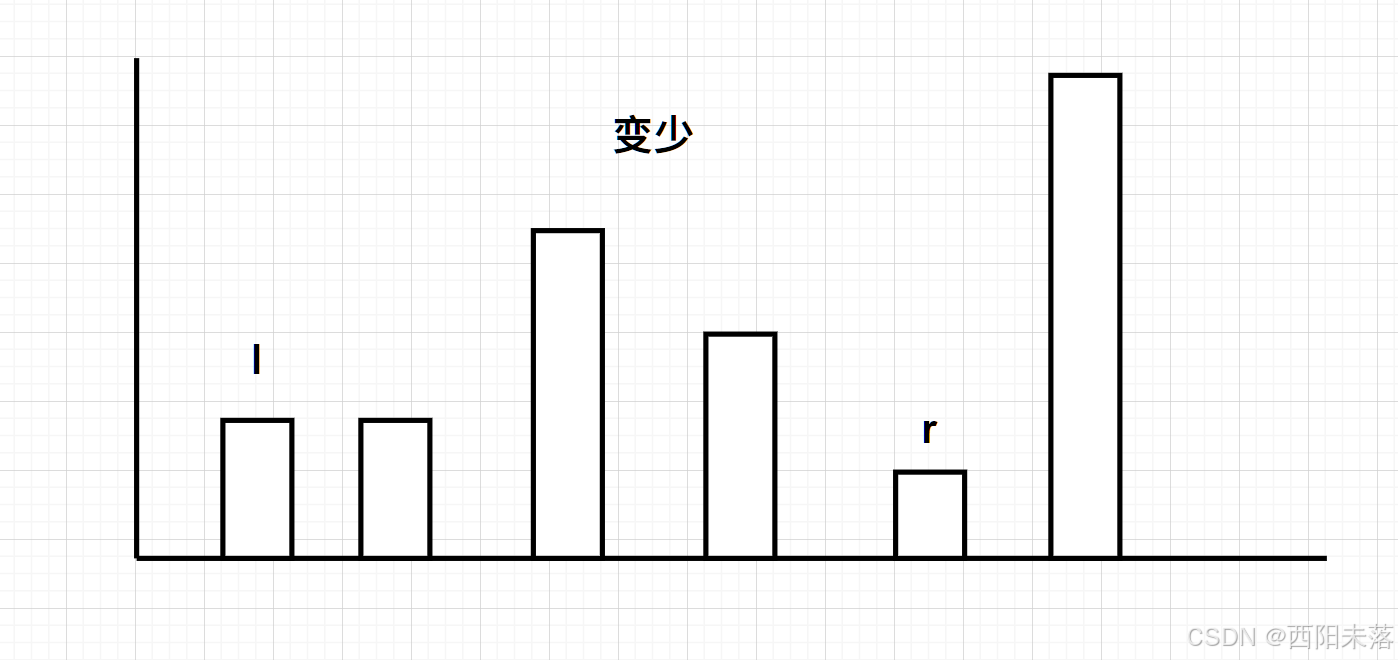
1、当我们的当前最左端要小于当前最右端的时候，是移动左好还是右好呢，其实是左更好，因为移动右边只可能是不变或是下降。如图：

所以我们这里要的是左指针右移

2、当我们的当前最左端要大于等于当前最右端的时候，其实是选择右端左移更好（和上面类似的逻辑）。

于是我们就有了我们的实现步骤了：

1、定义两个指针，一个指向了开头，一个指向了结尾处并且定义一个最大值给成负值。

2、设置循环逻辑（左指针不能大于我们的右指针），计算我们的当前最大值，然后进行左右的判断，当左边更高的时候就是我们的右指针左移，当是我们的右边更高的时候就是我们的左指针右移了，最后我们返回我们的最大值。

实现代码

class Solution {
public:int maxArea(vector<int>& a) {int l = 0, r = a.size() - 1;int Max = -1;while(l < r) {Max = max((r - l) * min(a[l], a[r]), Max);if(a[r] > a[l]) {l++;}else {r--;}}return Max;}
}; 

有效三角形的个数

题目描述

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

示例 2:

输入: nums = [4,2,3,4]
输出: 4

提示:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000

题目分析

其实这个题目和上面一个题目可以说是非常的像，首先我们还是给出我们一开始就能想到的写法吧，那就是写暴力，时间复杂度是O(n^3)

，很明显是过不了的。这里其实可以对题目做一个有技巧的拆分，那就是我们的考虑三个数不太好算，那么我们就先固定一个数，再考虑其他的。

实现思路

首先我们要知道我们的三角形的构成条件是任意两边之和都是要大于第三边的，我们这里为了不进行多次的判断可以将数组排个序，这样我们判断的时候就只要判断前面两个数大于第三边即可了，我们这里可以固定我们的最大的那么数，从比它小的数里面选出来两个，这个地方我们就可以用到我们的双指针了，因为我们这里就是要找到区间这个区间是从小到大的并且这个区间的左值和右值的和是大于我们的固定值的（区间符合的值就是我们的额区间长度-1（固定最右端的值，我们和前面的值组成一对即可）），实现步骤如下：

1、我们首先要做的就是对我们的数组进行排序。

2、固定我们的最大值，然后将次大值和最小值分别定义成右指针和左指针，遍历的时候分了两种情况：

a、左值加上右值大于我们的固定值，说明这个区间符合题意，进行我们的计算并加入结果，然后我们这里需要将右指针左移，因为我们这里计算包含右值的可能。

b、左值加上们的右值要小于等于我们的固定值，说明左值小了，我们将左指针右移。

实现代码

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(), nums.end());int r = nums.size() - 1;int ret = 0;for(int i = r; i >= 2; i--) {int l = 0, r = i - 1;while(l < r) {if(nums[l] + nums[r] > nums[i]) {ret += r - l;r--;}else {l++;}}}return ret;}
};

查找总价格为目标值的两个商品

题目描述

购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况，返回任一结果即可。

示例 1：

输入：price = [3, 9, 12, 15], target = 18
输出：[3,15] 或者 [15,3]

示例 2：

输入：price = [8, 21, 27, 34, 52, 66], target = 61
输出：[27,34] 或者 [34,27]

提示：

• 1 <= price.length <= 10^5
• 1 <= price[i] <= 10^6
• 1 <= target <= 2*10^6

题目分析

这个题目其实还是比较好做的，因为这个题目和上面几道题目还是很类似的，并且这个题目要比上面那几个简单，这个题目实际上就是我们双指针的常见套路，就是一个大区间缩小范围，这里的区间就是左值和右值之和是目标值。

实现思路

我们这里其实就是定义两个指针，一个左指针指向数组打开头，一个尾指针指向数组的结尾，然后在左指针不大于等于右指针的条件下循环即可，这里总共有三种可能：

1、我们的左值和右值和要大于我们的目标值，这个时候我们需要减小这个左右的和，于是我们可以将我们的右指针左移即可。

2、我们的左值和右值和要小于我们的目标值，这个时候我们就要加大我们的左右和，于是我们可以将左指针右移。

3、我们的左值和右值和等于了我们的目标值，这个时候我们直接返回即可了。

实现代码

class Solution {
public:vector<int> twoSum(vector<int>& price, int target) {sort(price.begin(), price.end()); // 这里可以无视掉，当时没看到说了是升序（bushi）int l = 0, r = price.size() - 1;while(l < r) {if(price[l] + price[r] > target) {r--;}else if(price[l] + price[r] < target){l++;}else {return {price[l], price[r]};}}return {-1, -1}; // 虽然题目没说有这个情况，但是我们为了代码有返回值还是象征性的写一下}
};

四数之和

题目描述

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案 。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

提示：

• 1 <= nums.length <= 200
• -109 <= nums[i] <= 109
• -109 <= target <= 109

题目分析

这个题目其实是三数之和的拓展题，感兴趣的朋友可以去看看，逻辑是类似的，但是我们这个题目更难一点。这个题目其实难的不是写的思路，这个思路想到了还是很好写的，最难的是这里的边界情况的处理，可以说是非常的恶心，感觉面试喜欢考这种题（bushi）。其实这个题目还是要有做三数之和题目的整体思路，因为这个题目相比三数之和就是多出来了一层循环，所以这个题目的数量级也是要比我们的三数之和要低的，这里我们基本思路就是将两个数固定下来，然后处理剩下的两个数即可。

实现思路

首先我们这里需要固定两个值，这两个值是数组中较小的值，然后我们的目标就变成了在剩下的后面的区间里面找到和为target - a - b的值，寻找这个值就成了我们之前查找总价格为目标值的两个商品这个题目的流程了，所以我们这里的思路还是比较简单的，但是我们这里题目中要求了不能重复，所以我们这里会有很多的边界条件的处理，首先我们这里来说两个简单发现的去重逻辑，分别是固定第一个数的时候和固定第二个数的时候我们的后续不能和之前的值有重复，接下来就是我们后两个数的处理了，我们这里的处理思路如下：

1、我们到了统计答案的时候，我们处理完了是会将左右指针向里收缩的，所以我们这里处理的方向一定要搞清楚

a、当我们的右值和前面的值重复的时候，我们需要将右指针向左移动，前提是右指针左边的那个指针要大于我们的左指针。

b、当我们的左值和后面的值重复的时候，我们需要将左指针向右移动，前提是左指针右边的那个指针要小于我们的右指针。

2、收缩区间，将我们的右指针左移，左指针右移。

实现代码

class Solution 
{
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> temp;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n - 3; i++) {if (i > 0 && nums[i] == nums[i - 1]) continue;for (int j = i + 1; j < n - 2; j++) {if (j > i + 1 && nums[j] == nums[j - 1]) continue;long long k = (long long)((long long)(target - nums[i]) - nums[j]);int l = j + 1, r = n - 1;while (l < r) {if (nums[l] + nums[r] < k) {l++;} else if (nums[l] + nums[r] > k) {r--;} else {temp.push_back({nums[i], nums[j], nums[l], nums[r]});while (r - 1 > l && nums[r] == nums[r - 1]) {r--;}while (l + 1 < r && nums[l] == nums[l + 1]) {l++;}r--, l++;}}}}return temp;}
};