机器学习实践项目(一)- Rossman商店销售预测 - 模型训练
由于本项目预测的是商店的销售价格,属于“连续”数值,因此是“回归(Regression)”类型的问题,常用的算法为线性回归、随机森林回归、XGBoost、神经网络,我们用的是XGBoost,对应的评估训练效果的方法为 均方根百分比误差(Root Mean Square Percentage Error (RMSPE)),下面给出Python实现。
def rmspe(y, yhat):return np.sqrt(np.mean(1 - yhat/y)**2)def rmspe_xg(yhat, y):y = np.expm1(y.get_label())yhat = np.expm1(yhat)return 'rmspe', rmspe(y, yhat)
评估函数定义完了以后,就开始配置参数进行训练。
params = {'objective':'reg:linear', # 目标任务:线性回归'booster':'gbtree', # 基学习器:梯度提升树(默认)'eta':0.03, # 学习率:控制每棵树的权重,防止过拟合'max_depth': 10, # 树的最大深度:控制模型复杂度'subsample': 0.9, # 样本采样率:每棵树使用90%的样本'colsample_bytree': 0.7, # 特征采样率:每棵树使用70%的特征'silent': 1, # 静默模式,不输出训练过程信息'seed': 10} # 随机种子
num_boost_round = 6000 # 最大 boosting 轮次
dtrain = xgb.DMatrix(X_train, y_train) # 训练数据
dvalid = xgb.DMatrix(X_validate, y_validate) # 验证数据
validationlist = [(dtrain, 'train'), (dvalid, 'eval')] # 监控数据集print('模型训练开始...')
start = time.time()
gbm = xgb.train(params,dtrain,num_boost_round,evals = validationlist,early_stopping_rounds = 100, # 早停轮次:验证集性能100轮无改善则停止custom_metric=rmspe_xg, # 自定义评估指标verbose_eval = True)
end = time.time()
print('Training time: %.3f' % (end - start))
训练完毕后,可以保存模型参数,以利于下次使用。
gbm.save_model('./train_model.json')
模型训练结束后,就可以用验证集X_validate作为参数丢给模型,预测出yhat,并利用yhat和验证集的真实值y_validate进行比较,看预测的效果。
print('验证数据表现:')
# 排序的目的是确保验证集中的参数部分X_validate和结果部分y_validate保持排序一致
X_validate.sort_index(inplace = True)
y_validate.sort_index(inplace = True)# 利用训练完的模型进行验证
yhat = gbm.predict(xgb.DMatrix(X_validate)) # yhat变量存放的是对验证集进行预测的销售金额
# 计算均方误差
error = rmspe(np.expm1(y_validate), np.expm1(yhat)) # y_validate是验证集中真实的销售金额,这里计算预测的值和真实值之间的均方误差
print('rmspe:', error)
打印出来的rmspe的值约小说明预测结果越接近真实值。

为了直观地观察结果,我们把X_validate, y_validate, yhat合并起来,并计算一些指标(Ratio/Error/Weight等),然后用折线图画出来。
res = pd.DataFrame(data = y_validate) # 把y_validate放在一个新数据集
res['Prediction'] = yhat # 把预测的yhat和y_validate放在一个数据集中res = pd.merge(X_validate, res, left_index = True, right_index = True) # 把res合并到X_validate中,这时,验证集中就包含了真实的销售金额和预测的销售金额res['Ratio'] = res['Prediction'] / res['Sales'] # 预测金额除以真实金额,大于1则预测金额偏大,小于1则预测金额偏小
res['Error'] = abs(1 - res['Ratio']) # 求预测金额和真实金额差距比率的绝对值
res['weight'] = res['Sales'] / res['Prediction'] # 真实金额除以预测金额得出权重,权重大于1则预测金额偏小,权重小于1则预测金额偏大plt.rcParams['font.family'] = 'STFangsong' #设置字体
col_1 = ['Sales', 'Prediction']
col_2 = ['Ratio']shops = np.random.randint(1, 1116, size = 3) # 随机在1~1115之间生成3个商店编号print('全部商店预测值和真实销量的比率是%0.3f' % res['Ratio'].mean()) # 打印全部商店平均的预测值和真实值的比率for shop in shops:cond = res['Store'] == shop # 根据随机生成的门店编号,抽取该门店所有数据df1 = pd.DataFrame(data = res[cond], columns = col_1)df2 = pd.DataFrame(data = res[cond], columns = col_2)df1.plot(title = '%d商店的预测数据和真实销量的对比' % shop, figsize = (12, 4))
所有门店平均的Ratio如下:

3个门店在验证集上的预测值和实际值的折线图如下:
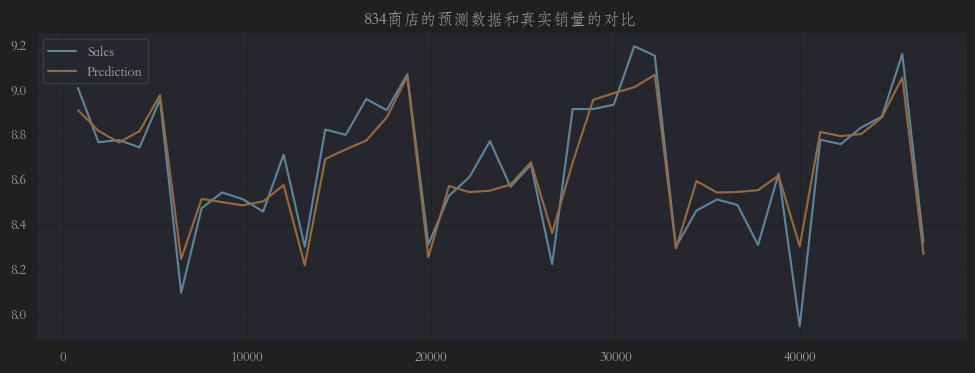
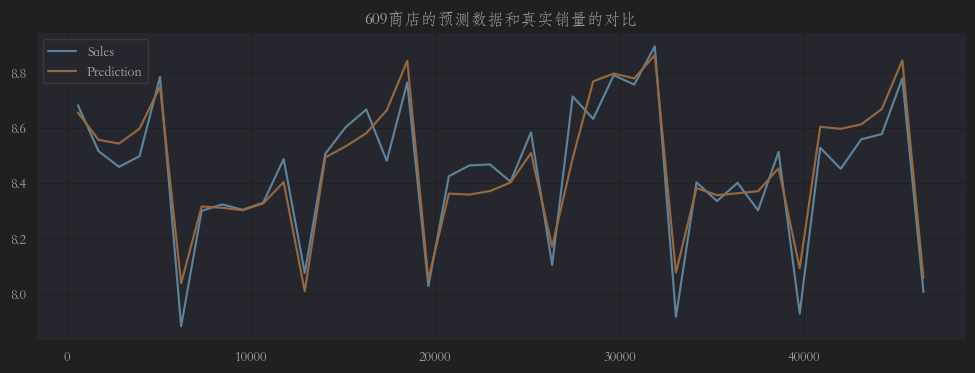
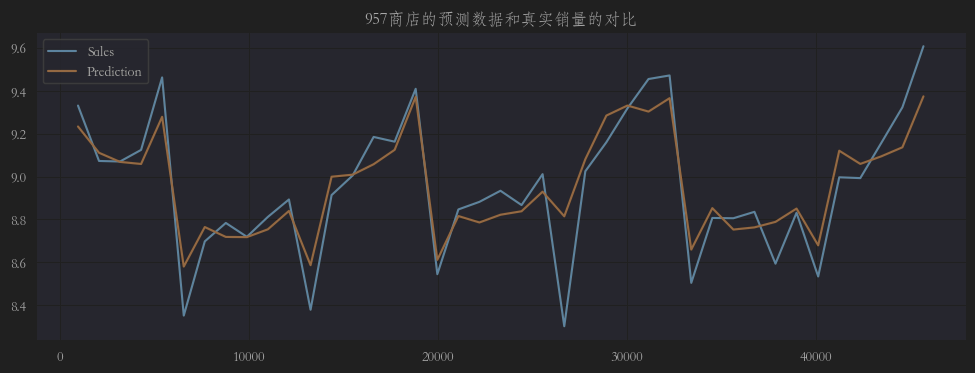
从图上可以看出,预测值和真实值还是有那么点偏差的,且整体比实际值高了那么一点点(1.001),所以我们最好需要对预测结果进行微调。
