从零复现论文(2)——:基于启发式优化的无线传感器网络WSN功率分配策略
1.主题
文章来自于一个2015年的会议,有点水,因此笔者在文章的基础上进行了进一步地实验,文章短小精悍,思路清晰,结合代码很容易让人理解,适合新手入门。
文章题目:Particle swarm optimization implementation for minimal transmission power providing a fully-connected cluster for the Internet of Things
文章链接:http://ieeexplore.ieee.org/abstract/document/7224573/

这篇论文聚焦物联网(IoT)中无线传感器网络(WSN)的能量优化问题,通过设计粒子群优化(PSO)算法,在保证传感器集群 “全连接” 的前提下,为每个节点计算最小传输功率,最终实现能量节省。
2.创新点
文章的创新点比较薄弱,方法老旧,但是处理问题的流程很值得借鉴,提供了一种典型的功率优化的问题范式!姑且一看罢!
1.首次将 PSO 用于 “单集群 WSN 的个性化传输功率优化”
2.提供了 “可复现的技术框架”(包括连通性判断、PSO 参数、实验场景)
本文再此基础上对比了不同的优化算法解决此类问题,提供了第3个创新点:
3.利用改进的PSA优化算法(APSA),并将这种方法和GWO,PSO优化进行对比,在这种功率优化问题下给出了更高效鲁棒的方案。
3.文章内容
要找到无线传感器网络中每个节点连接所需的最小功率,最理想的解决方案是:对于位于网络边缘的传感器节点,计算其仅需达到最近邻节点的最小功率;对于中间节点,则计算其连接边节点所需的最小功率。然而,随着集群内节点数量的增加,持续检查最近邻节点并保持全网连通将导致计算开销激增。因此,可以采用次优但计算强度较低的解决方案。粒子群优化算法(PSO)就是其中一种可行方案,本提案将对此进行探讨。
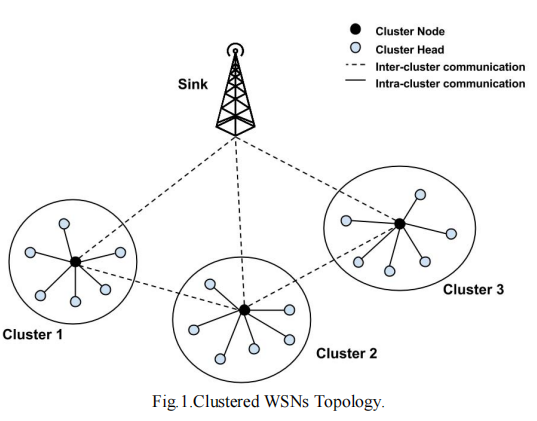
3.1系统模型
粒子群的过程不再赘述,本文令每个节点的当前功率作为粒子进行迭代,目标是网络整体消耗功率最低。
接收和发射功率用以下公式表示:
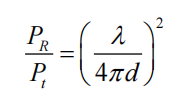
代码表示为:(其实就是计算路损的)
function [ATTdb] = friss(Gt, Gr, freq, Txp, Rxp)c = (3.*10.^8);
lambda = c ./ (freq.*10.^6);dist = (((Rxp(1) - Txp(1)).^2) + ((Rxp(2) - Txp(2)).^2)).^0.5;ATT = Gt.*Gr.*(lambda./(4.*pi.*dist)).^2;
ATTdb = 10.*log10(ATT);
end
粒子更新的核心公式:
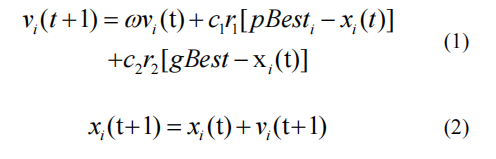
3.2提出问题
问题构建为一个优化问题,将整体节点的消耗的总功率变得最小
初始化场景中20个节点,作为随机生成的节点,具有随机的位置和功率
(1)求解传播损耗
根据上述FRISS进行路损的计算,每次都按照距离来计算节点间通信所消耗的功率
(2)求邻接矩阵,初步判断网络连通性
当节点的消耗功率过大,则视为这个节点成为空洞节点,整个网络不能联通
(3)构建网络的拉普拉斯矩阵,根据Fiedler准则,用第二小特征值判断网络连通性
即使所有节点都有邻居(D(i)≠0),网络仍可能不连通(如分成多个独立子集群),就是相当于各立山头的感觉。此处用代码表示:
% 步骤1:构建网络的拉普拉斯矩阵L(用于特征值分析)% 拉普拉斯矩阵定义:L(i,j) = 节点i的度(D(i)),当i=j;L(i,j) = -1,当i≠j且A(i,j)=1;否则L(i,j)=0for i = 1:Nfor j = 1:Nif i == j % 对角线元素:节点i的度(邻居数)L(i,j) = D(i);elseif A(i,j) == 1 % 非对角线且有连接:-1L(i,j) = -1;else % 非对角线且无连接:0L(i,j) = 0;endendendend
% 步骤2:计算拉普拉斯矩阵的所有特征值(eig(L)返回矩阵L的特征值向量)autovetor = eig(L); % autovetor(葡萄牙语:特征值向量,变量名可能是笔误,应为autovalor)% 步骤3:根据Fiedler理论判断连通性% Fiedler准则:拉普拉斯矩阵的第二小特征值(Fiedler值)>0 → 网络完全连通;否则不连通% 注:eig(L)返回的特征值默认无序,需注意"第二小"的判断(此处默认特征值已按升序排列,实际可加sort排序)if autovetor(2) > 0 % 第二小特征值>0,网络连通% 计算总传输功率(dBm):先求瓦特总和,再转dBm% 公式:总功率(dBm) = 10×log10(总功率(W)/1e-3) (W转dBm的标准公式)soma = 10.*log10((sum(power_vector_watt))/(1e-3));else % 第二小特征值≤0,网络不连通soma = Inf; % 返回无穷大惩罚end此处soma就是目标函数的输出,也就是优化目标
用数学语言描述的话就是:
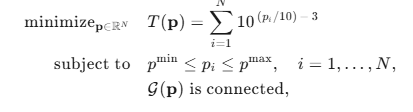
连通条件是一个二院假设检验条件
3.3实验方法
相关的约束目标函数的代码为:
%#################################################################################################################################################################################
% 该函数是WSN传输功率优化的核心辅助函数,用于:
% 1. 计算节点间的通信链路质量(基于Friss传播模型)
% 2. 判断网络是否完全连通(通过邻接矩阵、拉普拉斯矩阵特征值分析)
% 3. 若网络连通,返回总传输功率(dBm);若不连通,返回无穷大(Inf)作为惩罚
% 论文来源:"Particle swarm optimization implementation for minimal transmission power providing a fully-connected cluster for the Internet of Things"
% 论文访问:http://ieeexplore.ieee.org/abstract/document/7224573/
% 作者:Gabriel Lobão, Felipe Reis, Jonathan de Carvalho 和 Lucas Mendes
%#################################################################################################################################################################################% 函数定义:输入节点坐标矩阵和传输功率向量,输出总功率(连通时)或Inf(不连通时)
% X: 节点坐标矩阵,格式为[维度×节点数](如2×20表示20个节点的二维坐标)
% power_vector: 每个节点的传输功率向量(单位:dBm),长度=节点数(如[P1, P2, ..., PN])
% soma: 输出结果,连通时为总传输功率(dBm),不连通时为Inf
function [soma] = connect_report(X,power_vector)% 输入参数说明(补充注释,方便理解)
% X 节点坐标矩阵
% power_vector 每个节点的传输功率向量
% power_vector = [ P1 P2 P3 ... PN ] (功率向量格式示例)% 获取节点总数:X的列数=节点数(size(X,2)表示矩阵X的第二维度长度)
N = size(X,2); % 节点数量% N = 20;
freq = 915; % 固定通信频率为915MHz,WSN常用免授权频段% 初始化链路损耗矩阵:N×N矩阵,cost(l,c)表示节点l到节点c的信号传播损耗(单位:dB)
cost = zeros(N); % matriz de N-por-N posições (N×N维度的损耗矩阵)% 双重循环计算每个节点对(l→c)的传播损耗
for l=1:N % l:发送节点(transmitter)for c=1:N % c:接收节点(receiver)% 若发送节点=接收节点(自身到自身),损耗设为负无穷(无实际通信意义)if l == ccost(l,c) = -Inf;else% 调用Friss传播模型计算l到c的损耗(Friss模型是无线通信常用的远距离损耗模型)% FRISS(1,1,freq, X(:,l), X(:,c)):假设发射/接收天线增益=1,输入频率和节点坐标cost(l,c) = FRISS(1,1,freq, X(:,l), X(:,c));endend
end% 创建本地测试用的功率向量
% for i = 1:N
% % power_vector(i) = (randi(50,1,1)/10)-10.5; (随机生成功率)
% power_vector(i) = -20.371; (固定功率值测试)
% % % 原因:dBm是相对功率(便于计算损耗),但总功率求和需用绝对功率(瓦特),故需转换
% 转换公式:P(W) = 10^[(P(dBm)/10) - 3] (dBm转W的标准公式,1 dBm = 10^-3 W × 10^(P(dBm)/10))
for i = 1:Npower_vector_watt (i) = 10.^((power_vector(i)./10)-3);
end% 计算每个节点的接收功率
% 说明:PR(l,c)表示"节点l发送,节点c接收"时的接收功率(单位:dBm)
% 接收功率公式:PR = 发射功率(dBm) - 传播损耗(dB)(损耗是信号衰减,故用减法)
% 该循环计算发送节点为l时,各接收节点(列)的接收功率
PR = zeros(N); % PR - matriz de potência recebida. (N×N接收功率矩阵)% 双重循环计算所有节点对的接收功率
for l = 1: N % l:发送节点for c = 1 : N % c:接收节点% 接收功率 = 发送节点l的功率 + 损耗(cost(l,c)为负,等效于"发射功率 - |损耗|")PR(l,c) = power_vector(l) + cost(l,c);end
end% 分析节点间是否存在有效通信连接
% 邻接矩阵A:A(l,c)=1表示节点l和c可通信,A(l,c)=0表示不可通信
A = zeros(N); % Matriz adjacencia (N×N邻接矩阵,描述网络拓扑连接关系)
for l = 1:N % l:发送节点for c = 1: N % c:接收节点% 通信阈值:接收功率≥-60 dBm(WSN常用的最小接收灵敏度,低于该值无法正确解调信号)if PR(l,c) >= -60 A (l,c) = 1; % 接收功率达标,标记为"可通信"elseA (l,c) = 0; % 接收功率不达标,标记为"不可通信"endend
end% 计算每个节点的"出度":D(i)表示节点i能直接通信的邻居节点数量(A(i,:)是节点i的所有出边)
for i=1:ND(i) = sum(A(i,:)); % sum(A(i,:)):求和节点i的邻接行,得到邻居数
end% 初步判断网络连通性:connect为0表示不连通,为1表示暂未发现孤立节点(需进一步验证)
connect = 1;
for i = 1:N% 若任一D(i)=0,connect会被乘为0(逻辑:只要有一个节点孤立,connect=0)connect = D(i).*connect;
end% (关键说明:即使所有节点都有邻居(D(i)≠0),网络仍可能不连通(如分成多个独立子集群);
% 需用Miroslav Fiedler的理论:通过拉普拉斯矩阵的第二小特征值判断网络连通性——第二小特征值>0则连通)% 分情况计算输出结果soma
if connect == 0 % 情况1:存在孤立节点(D(i)=0),网络不连通% 计算“不连通程度”:孤立节点数量(越多,损失越大)isolated_num = sum(D == 0); % D(i)=0 表示节点i孤立% 基础惩罚值(足够大的有限值,确保连通配置更优) + 孤立节点损失soma = 100 + isolated_num * 10; % 孤立节点越多,soma越大
else % 情况2:所有节点都有邻居,需进一步用拉普拉斯矩阵验证连通性% 步骤1:构建网络的拉普拉斯矩阵L(用于特征值分析)% 拉普拉斯矩阵定义:L(i,j) = 节点i的度(D(i)),当i=j;L(i,j) = -1,当i≠j且A(i,j)=1;否则L(i,j)=0for i = 1:Nfor j = 1:Nif i == j % 对角线元素:节点i的度(邻居数)L(i,j) = D(i);elseif A(i,j) == 1 % 非对角线且有连接:-1L(i,j) = -1;else % 非对角线且无连接:0L(i,j) = 0;endendendend% 步骤2:计算拉普拉斯矩阵的所有特征值(eig(L)返回矩阵L的特征值向量)autovetor = eig(L); % autovetor(葡萄牙语:特征值向量,变量名可能是笔误,应为autovalor)% 步骤3:根据Fiedler理论判断连通性% Fiedler准则:拉普拉斯矩阵的第二小特征值(Fiedler值)>0 → 网络完全连通;否则不连通% 注:eig(L)返回的特征值默认无序,需注意"第二小"的判断(此处默认特征值已按升序排列,实际可加sort排序)if autovetor(2) > 0 % 第二小特征值>0,网络连通% 计算总传输功率(dBm):先求瓦特总和,再转dBm% 公式:总功率(dBm) = 10×log10(总功率(W)/1e-3) (W转dBm的标准公式)soma = 10.*log10((sum(power_vector_watt))/(1e-3));else % 第二小特征值≤0,网络不连通soma = Inf; % 返回无穷大惩罚end
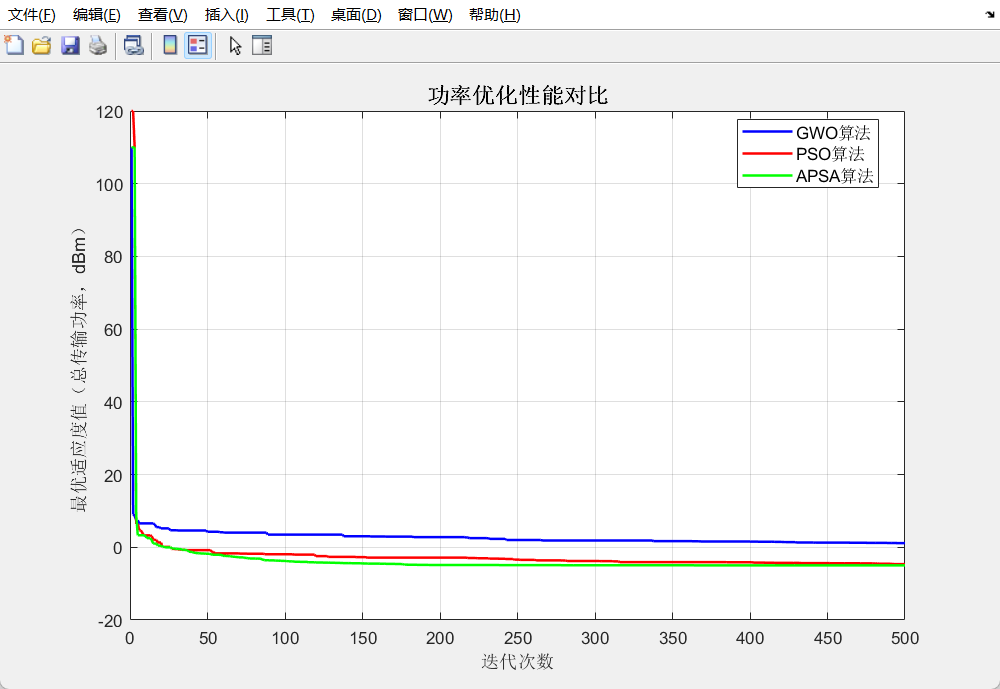
endend % 函数结束笔者选择了一个典型场景进行测试,对比了GWO、PSO、APSA优化的效果,
核心的代码如下所示:
disp(['===== 开始测试 ', num2str(t), ' =====']);% fprintf(fid, '##########################################################\n');% fprintf(fid, ' 测试 %d \n', t);% fprintf(fid, '##########################################################\n\n');% 算法通用参数设置sizepop = 30; % 种群规模Max_iter = 500; % 最大迭代次数dim = size(X, 2); % 问题维度(节点数量,此处为20)% 传输功率范围(dBm)pMin = -30;pMax = 0;% 设置边界(每个节点功率范围:-30~0 dBm)lb = pMin * ones(1, dim); % 功率下限向量(1×20)ub = pMax * ones(1, dim); % 功率上限向量(1×20)% 定义目标函数(输入功率向量,输出适应度)fobj = @(x) wsn_objfun(x, X);% ==================================================% 运行GWO算法(注意:GWO函数返回值顺序需匹配其定义)% ==================================================disp('正在运行GWO算法...');tic; % 开始计时% 修正:根据GWO函数定义,返回值应为 [最优适应度, 最优位置, 收敛曲线]% GWO_best_position 每个节点的最优传输功率配置% GWO_best_fitness 网络全连通时的最小总传输功率% GWO_Convergence_curve 500 次迭代中每次的最优总功率(最后一个值就是best_position)[GWO_best_fitness, GWO_best_position, GWO_Convergence_curve] = GWO(sizepop, Max_iter, lb, ub, dim, fobj);GWO_time = toc; % 记录GWO运行时间% ==================================================% 运行PSO算法(参数顺序已修正:fobj, dim, lb, ub, sizepop, Max_iter)% ==================================================disp('正在运行PSO算法...');tic; % 开始计时[ PSO_best_fitness, PSO_best_position,PSO_Convergence_curve] = PSO(sizepop,Max_iter, lb, ub, dim,fobj );WSN_P = X;[ APSA_best_fitness, APSA_best_position,APSA_Convergence_curve] = APSA(fobj,WSN_P,dim, lb, ub, sizepop, Max_iter);PSO_time = toc; % 记录PSO运行时间% [gBestScore,gBest,cg_curve]=PSO(N,Max_iteration,lb,ub,dim,fobj)% ==================================================% 命令行输出时间与最优结果对比% ==================================================disp(['测试 ', num2str(t), ' 时间对比:']);disp([' GWO算法运行时间: ', num2str(round(GWO_time, 4)), ' 秒']); % 保留4位小数,更清晰disp([' PSO算法运行时间: ', num2str(round(PSO_time, 4)), ' 秒']);disp([' 最优总功率对比: GWO=', num2str(round(GWO_best_fitness, 4)), ' dBm, PSO=', num2str(round(PSO_best_fitness, 4)), ' dBm']);disp(' ');当前场景中的网络架构里节点的位置为:
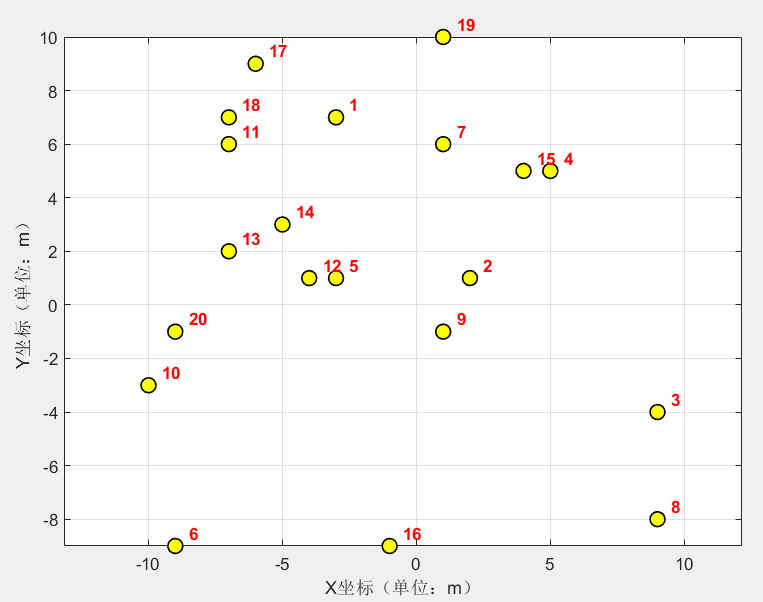
代码运行结果,可以看出笔者提出的优化算法明显可以更好的迭代效果: