自然语言处理分享系列-词语和短语的分布式表示及其组合性(一)
目录
一、摘要
连续 Skip-gram 模型及其改进
词表示的局限性及短语处理
二、介绍
分布式词向量的作用
Skip-gram模型的创新
模型扩展与优化
短语向量的必要性
向量加法组合性
三、skip-gram模型
分层 Softmax
一、摘要
连续 Skip-gram 模型及其改进
近期提出的连续 Skip-gram 模型是一种高效方法,能够学习高质量的分布式词向量表示,捕捉大量精确的句法和语义词汇关系。本文提出多项改进,既提升了词向量的质量,也加快了训练速度。通过对高频词进行子采样,显著加速训练过程,同时学到更规则的词表示。此外,还提出一种称为负采样的简单替代方案,以取代层次化 Softmax。
词表示的局限性及短语处理
词向量的固有局限在于无法反映词序,也难以表示惯用短语。例如,“Canada”和“Air”的语义无法简单组合为“Air Canada”。受此启发,本文提出一种从文本中发现短语的简单方法,并证明为数百万短语学习优质向量表示是可行的。
二、介绍
分布式词向量的作用
词在向量空间中的分布式表示通过将语义相似的词聚集在一起,帮助学习算法在自然语言处理任务中取得更好性能。词表示的最早应用可追溯至1986年Rumelhart、Hinton和Williams的研究[13],后续在统计语言建模中取得了显著成功[1]。这一思想还被应用于自动语音识别、机器翻译[14, 7]以及多种NLP任务[2, 20, 15, 3, 18, 19, 9]。
Skip-gram模型的创新
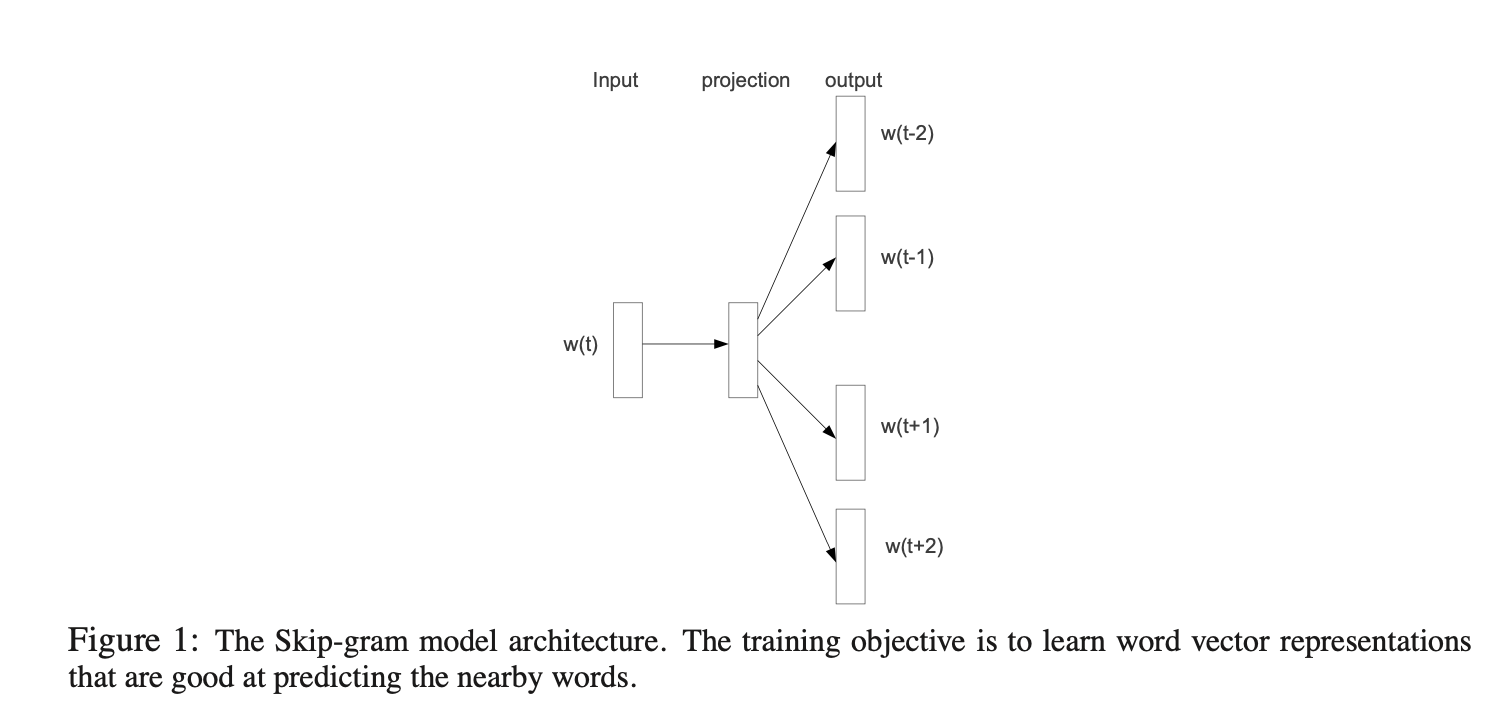
Mikolov等人[8]提出的Skip-gram模型是一种高效方法,可从海量非结构化文本数据中学习高质量词向量。与多数传统神经网络架构不同,Skip-gram模型的训练(如图1所示)不涉及密集矩阵乘法运算,因此效率极高:经优化的单机实现可在一天内处理超过1000亿词。
神经网络生成的词向量具有语言学意义,许多语义模式可表示为线性变换。例如,向量计算vec("Madrid") - vec("Spain") + vec("France")的结果更接近vec("Paris")而非其他词向量[9, 8]。
模型扩展与优化
对Skip-gram模型的扩展包括:
- 高频词下采样:训练时对高频词进行下采样,提速2-10倍,同时提升低频词表示的准确性。
- 简化NCE方法:采用简化的噪声对比估计(NCE)[4]替代传统分层softmax,显著加速训练并改善高频词向量质量。
短语向量的必要性
传统词向量无法表示非组合性短语(如"Boston Globe"作为报纸名,其含义并非"Boston"与"Globe"的简单叠加)。将短语视为独立单元进行训练可增强模型表达能力。短语识别采用数据驱动方法,训练时将其作为独立标记处理。评估时,类比推理任务包含词与短语组合,例如验证vec("Montreal Canadiens") - vec("Montreal") + vec("Toronto")是否最接近vec("Toronto Maple Leafs")。
向量加法组合性
Skip-gram模型展现的向量加法特性可生成有意义的组合结果。例如:
vec("Russia") + vec("river")接近vec("Volga River")vec("Germany") + vec("capital")接近vec("Berlin")
这表明,通过基础数学运算可获取词向量中隐含的语言理解能力。
三、skip-gram模型
Skip-gram模型的训练目标是找到能够有效预测句子或文档中上下文单词的词向量表示。其形式化定义为:给定一个训练单词序列w₁, w₂, w₃, ..., ,该模型的目标是最大化平均对数概率。
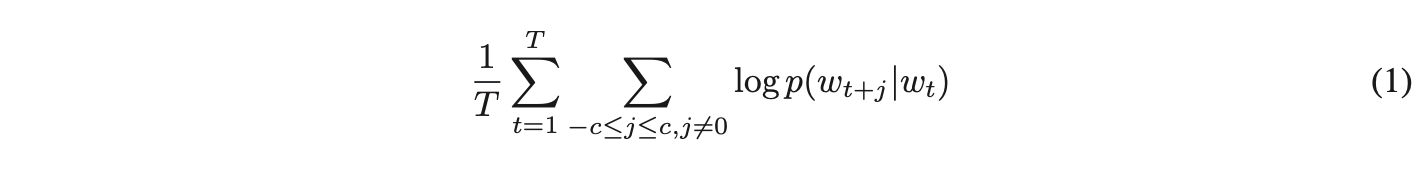
其中,( c ) 表示训练上下文的大小(可以是中心词 ( ) 的函数)。较大的 ( c ) 会生成更多训练样本,从而提高准确性,但代价是增加训练时间。基础的 Skip-gram 模型使用 softmax 函数定义 (
)。
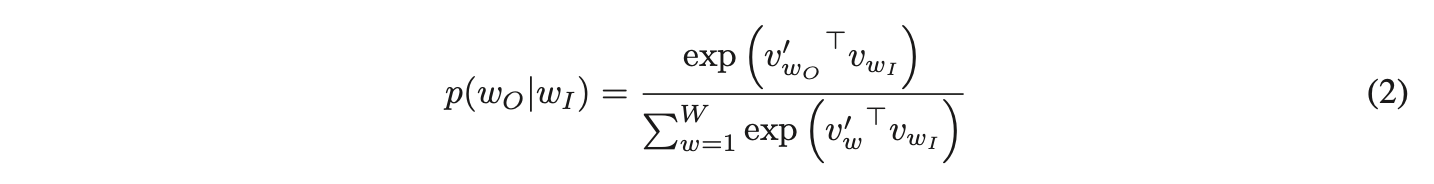
其中和
分别是单词w的“输入”和“输出”向量表示,W是词汇表中的单词数量。该公式在实际应用中不可行,因为计算∇logp(wO|wI)的成本与W成正比,而W通常非常大(词汇量在10^5到10^7量级)。
分层 Softmax
一种计算高效的完整 softmax 近似方法是分层 softmax。在神经网络语言模型的背景下,该方法由 Morin 和 Bengio [12] 首次提出。其主要优势在于,无需评估神经网络中的全部 个输出节点来获取概率分布,仅需评估约
个节点即可。
分层 softmax 使用二叉树的输出层结构,其中叶子节点对应词汇表中的 个词,每个内部节点显式表示其子节点的相对概率。这种结构通过随机游走机制为词汇分配概率。
具体而言,每个词 可通过从树根出发的特定路径到达。定义
为从根节点到
的路径上第
个节点,
为该路径长度,满足
且
。此外,对任意内部节点
,设
为其任意固定子节点,
在
为真时取值为 1,否则为 -1。分层 softmax 将条件概率
定义为:
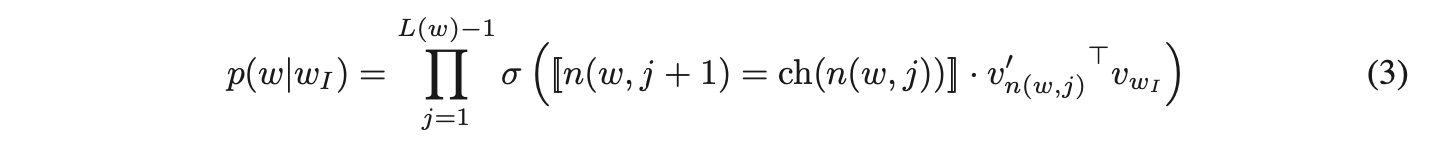
其中 σ(x) = 1/(1 + exp(−x))。可以验证![]() 。这意味着计算 log p(wO |wI ) 和 ∇ log p(wO |wI ) 的代价与 L(wO ) 成正比,平均而言不超过 log W。
。这意味着计算 log p(wO |wI ) 和 ∇ log p(wO |wI ) 的代价与 L(wO ) 成正比,平均而言不超过 log W。
与 Skip-gram 的标准 softmax 方法(为每个单词 w 分配两个表示 和
)不同,分层 softmax 方法为每个单词 w 分配一个表示
,并为二叉树的每个内部节点 n 分配一个表示
。
分层 softmax 使用的树结构对性能有显著影响。Mnih 和 Hinton 探索了多种构建树结构的方法,并分析了其对训练时间和模型准确性的影响 [10]。本工作采用二进制霍夫曼树,因为它为高频单词分配短编码,从而加快训练速度。此前已有研究表明,按词频分组是一种简单有效的神经网络语言模型加速技术 [5, 8]。
本篇内容就描述到这里,下一篇会继续进行负采样的讲解。
传送门:
