大数据成矿预测系列(四) | 成矿预测的“主力军”:随机森林与支持向量机深度解析
前言
随着地球科学进入大数据时代,传统的矿产勘查方法正面临着一场深刻的变革。从传统的统计学模型到现代的机器学习模型,成矿预测正经历着范式的转变。现代勘探工作流需要整合来源多样、结构复杂的海量数据集,包括地质填图、地球物理、地球化学以及高分辨率遥感影像 (当然还有钻孔数据等其他数据)。在这一背景下,机器学习是将这些海量数据转化为精准成矿预测图 (Mineral Prospectivity Mapping, MPM) 的核心引擎。
当然,从数据角度来看,地质大数据可以分为结构化数据,半结构换数据和非结构化数据。数据相关的内容我会在后续专门开一个系列讲述。这并不是这篇文章的重点。欢迎持续关注 “码上地球——数学地球科学” 获取后续内容。
在众多算法中,随机森林(Random Forest, RF)与支持向量机(Support Vector Machine, SVM)已成为该领域应用最广泛、最核心的两大“主力军” 。它们凭借强大的非线性关系建模能力,在地学数据分析中扮演着举足轻重的角色(论文中随处可见😂)。
本文旨在简单阐述其工作原理,讨论在成矿预测这一特定场景下,哪种算法更能应对地学数据独有的挑战。
随机森林
随机森林是一种集成学习算法,其核心思想与古语“三个臭皮匠,顶个诸葛亮”不谋而合。它并不依赖于某一个强大而复杂的单一模型,而是通过构建并结合数百个相对简单的决策树(Decision Trees)模型,来获得远超任何个体模型的稳定性和准确性 。
核心原理:地质专家的“群策群力”
可以将随机森林的工作机制比作一个大型、多元化的地质专家委员会,而非依赖一位全知全能的“宗师” 。委员会的每一位专家都是一棵决策树,而算法通过精巧的“双重随机”机制来确保专家团队的多样性和独立性,从而实现集体智慧。 而他的算法主要依赖于两个方面:
-
数据随机化:算法在训练每一棵决策树时,并非使用全部的训练数据(例如,所有已知的矿点和非矿点)。相反,它会从原始数据集中进行有放回的随机抽样,生成一个与原始数据集大小相同但内容不同的子集 。这意味着某些矿点样本可能在一棵树的训练集中出现多次,而另一些则可能完全不出现。这种机制保证了每棵树都是从一个略有不同的“地质视角”去学习成矿规律,从而避免了所有树都犯同样错误的风险。对于每棵树,大约有三分之一的原始数据未被抽中,这部分数据被称为“袋外数据”(Out-of-Bag, OOB),它们可以被用作一个天然的、无偏的内部验证集,用于评估模型性能而无需额外划分测试集 。
-
特征随机化:这是随机森林相较于其他集成算法 (Bagging) 的关键创新。在决策树生长的每一个节点需要进行分裂时,算法并不会在所有的证据图层(如磁异常、重力、地球化学元素、断裂距离等)中寻找最优分裂特征。它会先随机选择一个特征子集(例如,从全部30个图层中随机挑选5个),然后仅在这个子集内寻找最佳分裂点 。这一机制强制不同的决策树成为不同地质证据组合的“专家”。它有效防止了少数几个极其强大的预测变量(例如,一个非常显著的与成矿直接相关的地球化学异常)主导整个森林的决策过程,从而确保了模型的多样性,使得森林能够捕捉到更广泛、更细微的成矿模式 。
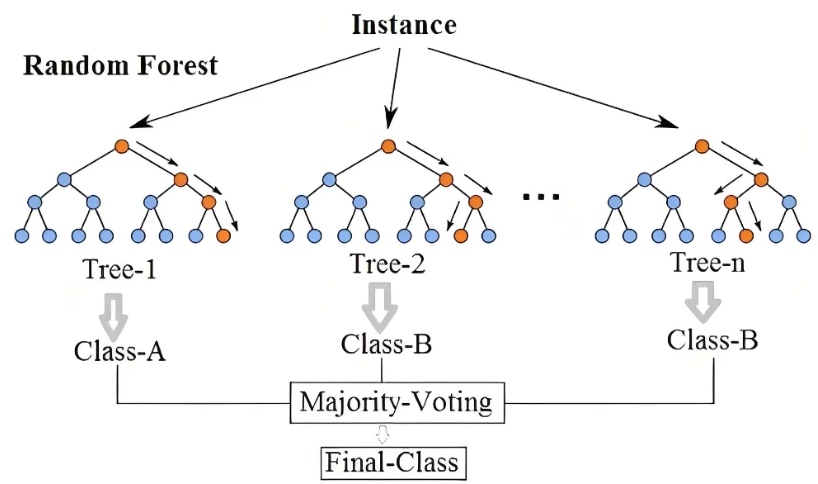
最终,当需要对一个新区域进行预测时,森林中的每一棵树都会独立地给出一个“有矿”或“无矿”的判断。算法会收集所有树的“投票”,并以少数服从多数的原则,做出最终的预测决策。
抗过拟合引擎:为何RF能驾驭地质数据
在成矿预测中,"过拟合"(Overfitting)是一个致命缺陷。一个过拟合的模型,会过度学习训练数据中(即已知矿点)的局部细节和噪声,以至于它能完美地“解释”所有已知矿点,但却失去了对未知区域的预测能力。用人话来说它记住的是“答案”,而非“规律”。
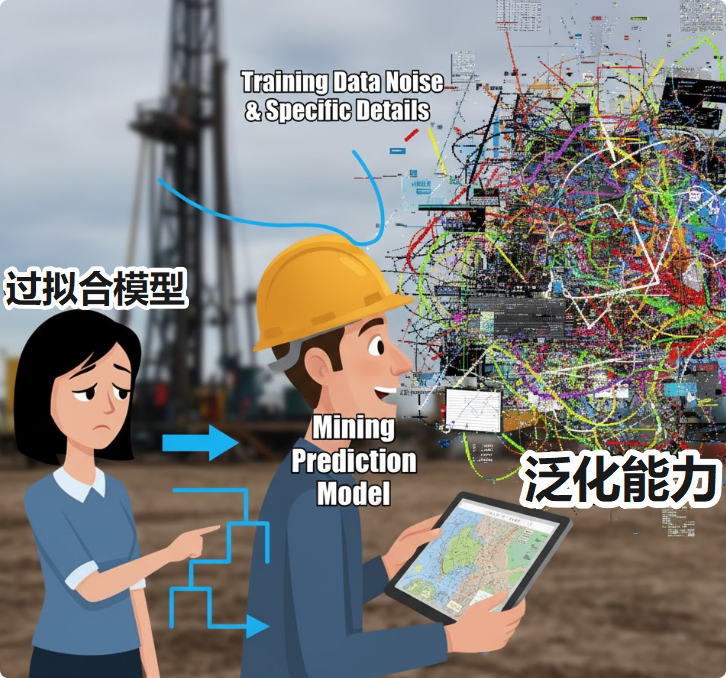
随机森林通过数据采样和特征选择的随机化,算法确保了森林中任意两棵树之间的相关性都非常低 。虽然单一的、深度生长的决策树极易过拟合,因为它会不断分裂以适应训练数据中的每一个微小波动。但是,当我们将数百个这样低偏差、高方差且互不相关的决策树的预测结果进行平均或投票时,它们各自的误差会相互抵消,从而显著降低整体模型的方差,得到一个既准确又稳健的最终模型 。正是这种机制,使得随机森林即使在树的数量很多时也不会出现过拟合问题,表现出极强的泛化能力 。这对于处理本身就充满噪声、复杂且“真理”(已知矿点)稀少的地质数据而言,是一项至关重要的优势。
地学应用的关键优势
除了强大的抗过拟合能力,随机森林还在三个方面展现出与地质勘查工作流高度契合的优势。
-
小样本学习能力:在勘查的早期阶段,尤其是“绿地”勘探中,可供模型学习的已知矿点(训练样本)往往非常稀少。有学者的研究说明,随机森林即便在训练样本数量极少的情况下,依然能够构建出有效且稳健的预测模型 。这对预算有限、勘探程度低的区域极具价值。
-
处理缺失值:地质数据集常常是不完整的,例如某些区域可能缺少某种地球化学采样或地球物理数据。许多算法无法直接处理这些缺失值,需要进行复杂的数据插补或直接丢弃样本。随机森林内置了高效的缺失值处理机制,能够在不牺牲数据完整性的前提下保持模型的准确性。
-
黑盒解译:机器学习模型常被诟病为“黑箱”,即它们能给出预测结果,却无法解释原因。随机森林通过其“特征重要性”评分功能,在很大程度上克服了这一缺陷。勘探管理者不仅能得到一张高潜力靶区图,还能得到一份数据驱动的报告,解释了为什么这些区域具有高潜力。例如,在某金矿成矿预测案例中,特征重要性分析可能揭示出,“与镁铁质火山岩的接触带”和“某特定走向的变形带”是控制成矿的最关键因素 。这种反馈不仅能验证和优化地质学家头脑中的成矿概念模型,甚至可能挑战传统认知,提出全新的、由数据驱动的勘探思路。这使得随机森林不再仅仅是一个圈定靶区的工具,而是成为了地质勘探科学研究流程中一个不可或缺的组成部分。
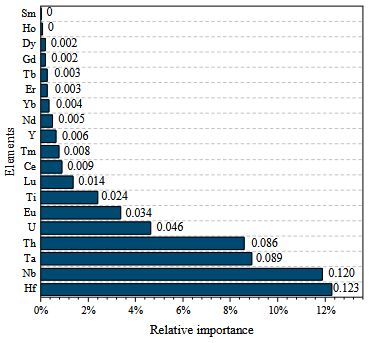
随机森林特征重要性图示例,图片来源:Wen et al., 2024
支持向量机
支持向量机是一种强大的监督学习算法,其核心思想是基于几何和最优化理论,在数据之间寻找一个最优的分类边界。它以其数学上的严谨性和处理复杂非线性问题的高效性而著称。
这是数学家最喜欢的模型之一,数学优雅!
核心原理:划分最清晰的“街道”
支持向量机本质上是一个非概率性的二元线性分类器 。其最基本的目标,是在代表不同类别(如“矿点”与“非矿点”)的数据点之间,找到一个最优的超平面(Hyperplane)——在二维空间中是一条直线,在三维空间中是一个平面,以此类推——将它们完美地分离开 。
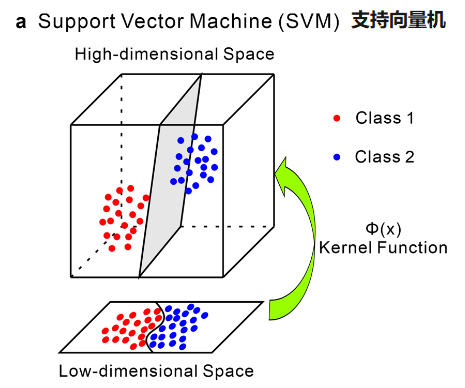
支持向量机原理示意图,图片来源:Zhong et al., 2023
在众多可以划分数据的超平面中,SVM 寻找的是那个“最优”的。这个“最优”的定义是:该超平面到两边最近的数据点的距离(即间隔,Margin)最大化 。这个概念可以通过一个生动的比喻来理解:想象一下要在代表两个不同社区的房屋(数据点)之间修建一条尽可能宽的街道(分类边界)。最优的街道就是那条在保证不拆迁任何房屋的前提下,路面最宽的街道 。
那些位于街道边缘、恰好“顶”在路肩上的房屋,被称为支持向量(Support Vectors)。它们是定义街道位置和宽度的关键点。所有其他远离街道的房屋,无论它们在哪里,都对街道的最终规划毫无影响。这使得SVM模型非常高效,因为它只关注那些最难区分、位于分类边界上的样本 。
核技巧:通往高维空间的捷径
在现实世界中,绝大多数地质成矿系统都不是线性可分的。面对这种复杂的非线性问题,SVM 采用了一种被称为“核技巧”(Kernel Trick)的精妙策略 。
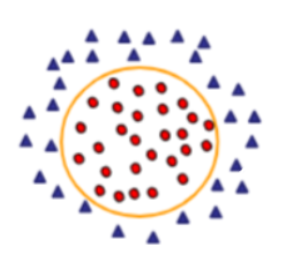
线性不可分的情况图,图片来源:网络
核技巧的核心思想是:如果在当前维度下数据是线性不可分的,那么就将数据映射到一个更高维度的空间中,使其变得线性可分 。这可以用一个比喻来解释:想象一张平铺在桌面上的纸,上面混杂着红色和蓝色的点,无法用一把直尺分开。但如果你将这张纸拿起并弯曲成三维形状,这些点在三维空间中可能就变得可以用一个平板(即一个超平面)轻易地分开了 。
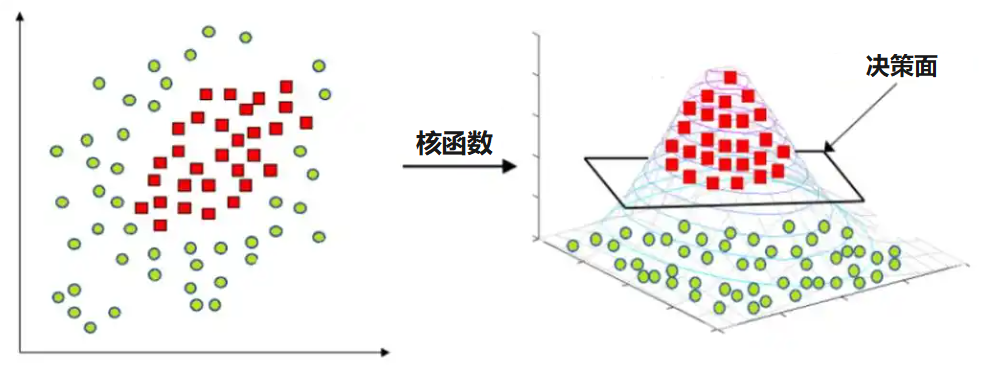
核函数“升维”图,图片来源:网络
而“技巧”之所以为“技巧”,在于 SVM 算法实际上无需真正地计算出每个数据点在这个高维空间中的新坐标。它通过一个核函数,如多项式核或高斯径向基函数(RBF)核,来直接计算数据点在高维空间中的內积(点积),而这正是 SVM 优化过程中唯一需要的信息。这种方法的计算成本远低于显式地进行维度转换,使得 SVM 能够以高效的方式处理高度复杂的非线性问题 。
地学优势
凭借核技巧,SVM 在理论上具备了模拟地质证据与成矿作用之间极其复杂的非线性关系的能力 。由于其算法是基于严格的数学最优化理论(寻找最大间隔),SVM 在处理给定的训练数据时,往往能够找到一个“完美”的分类边界,从而在训练集上达到非常高的分类精度 。
如上是理论上来说,现实情况是我在做大部分机器学习的情况下,支持向量机的效果只能说是中规中矩
对比
| 特征 | 随机森林 | 支持向量机 |
|---|---|---|
| 核心原理 | 集成学习:由大量简单的决策树“投票”形成集体、稳健的预测。 | 最大间隔分类器:寻找一个能以最大距离将不同数据类别分开的最优超平面(边界)。 |
| 非线性处理 | 隐式处理:通过决策树的一系列二元分裂,自然地捕捉复杂的非线性关系。 | **显式处理 (核技巧)**:将数据映射到更高维度,使其线性可分。 |
| 关键优势 (MPM) | 稳健性与可解释性:在小样本、含噪声或数据缺失的情况下表现优异;提供特征重要性排序。 | 高训练精度:在训练数据上能达到近乎完美的分类效果,对定义明确的问题非常强大。 |
| 关键劣势 (MPM) | 计算可能较为密集;可能偏向于具有多分类水平的特征。 | 高过拟合风险:在小样本下极易“记住”训练数据,导致泛化能力差;“黑箱”特性。 |
| 可解释性 | 高:内置的特征重要性可直接揭示哪些地质要素是预测的关键驱动力。 | 低:在高维空间中形成的决策边界无法被直观地地质学解释。 |
| 稀疏数据性能 | 优越:被证实即使在训练矿点极少的情况下依然稳定有效。 | 较差:过拟合风险高,导致对未知区域的预测能力不佳。 |
| MPM战略定位 | 发现新矿点:因其卓越的泛化能力和可解释性带来的战略价值,是大多数MPM任务,尤其是绿地/数据贫乏区的首选工具。 | 谨慎使用:功能强大,但更适用于拥有大量训练数据或定义明确的分类问题,而非预测性勘查。 |
End
成矿预测建模的最终目标,不是构建一个对过去(已知矿床)的完美复刻,而是创造一个对未来(未知矿床)的有效指引。在这一核心目标的指引下,随机森林已被反复证明在有限数据下具有更强的泛化能力,这使其成为一个更可靠、更有价值的工具 。
所以在对于成矿预测任务,随机森林应该是被推荐或者首先使用的算法。这也是本人所一直推荐的,对于一个快速需要验证可行性结果的任务而言,优先使用随机森林进行训练得到结果能有效提高决策成本。
最后的最后,欢迎持续关注 “码上地球——数学地球科学” 获取更多内容。

科学探索永无止境,本文仅为笔者个人学习总结。因知识所限,文中若有不当之处,敬请方家斧正。
参考内容
-
Carranza, E. J. M., & Laborte, A. G. (2015). Random forest predictive modeling of mineral prospectivity with small number of prospects and data with missing values in Abra (Philippines). Computers & Geosciences, 74, 60-70.
-
Lachaud, A., Adam, M., & Mišković, I. (2023). Comparative study of random forest and support vector machine algorithms in mineral prospectivity mapping with limited training data. Minerals, 13(8), 1073.
-
Carranza, E. J. M., & Laborte, A. G. (2016). Data-driven predictive modeling of mineral prospectivity using random forests: A case study in Catanduanes Island (Philippines). Natural Resources Research, 25(1), 35-50.
-
Wen, Z. H., Li, L., Kirkland, C. L., Li, S. R., Sun, X. J., Lei, J. L., ... & Hou, Z. Q. (2024). A machine learning approach to discrimination of igneous rocks and ore deposits by zircon trace elements. American Mineralogist, 109(6), 1129-1142.
-
Zhong, S. H., Liu, Y., Li, S. Z., Bindeman, I. N., Cawood, P. A., Seltmann, R., ... & Liu, J. Q. (2023). A machine learning method for distinguishing detrital zircon provenance. Contributions to Mineralogy and Petrology, 178(6), 35.
-
【机器学习】支持向量机(SVM)
