李宏毅机器学习笔记19

目录

摘要

Abstract

1.从矩阵看Self attention

2.Multi-head Self attention

3.Positional encoding

4.Truncated self attention

---

 

 

摘要

本篇文章继续学习李宏毅老师2025春季机器学习课程，学习内容是Self attention从矩阵角度的计算方法及一些Self attention应用。

Abstract

This article continues our study of Prof. Lee Hung-yi's 2025 Spring Machine Learning course, focusing on the computational approach of Self-attention from a matrix operations perspective and some applications of Self-attention.

1.从矩阵看Self attention

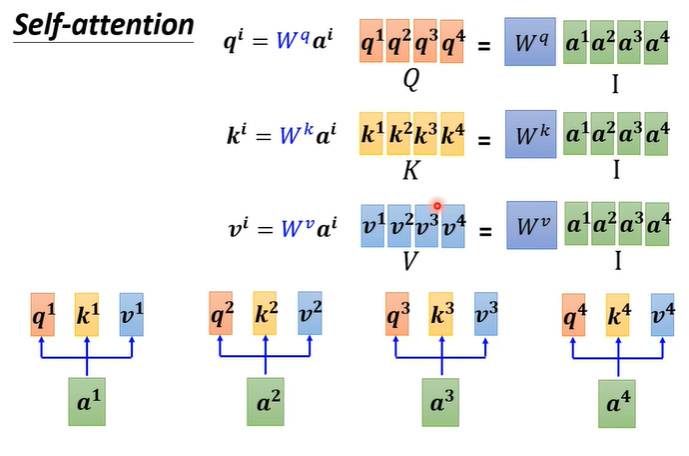
从矩阵角度来看Self attention关联度的计算，我们知道每个输入都需要产生q，k，v三个向量，我们将所有输入a合并视为一个矩阵I，将矩阵I与对应的矩阵相乘就能得到由q，k，v三种向量组成的矩阵Q,V,K。

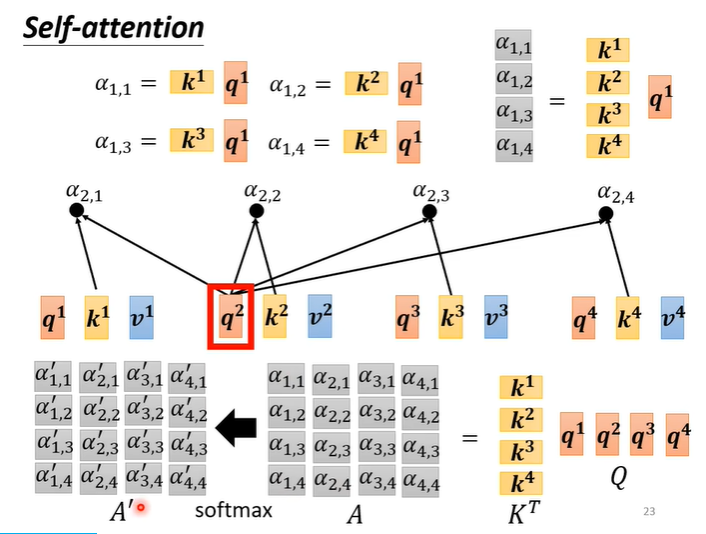
关联度计算是由向量q，k相乘得到，那么我们计算a1的关联度时需要所有的k与q向量相乘，即K矩阵的转置与q相乘。再扩大到所有，则变为K矩阵的转置与Q矩阵相乘，最后得到所有关联度的矩阵A，在经过soft-max得到矩阵。

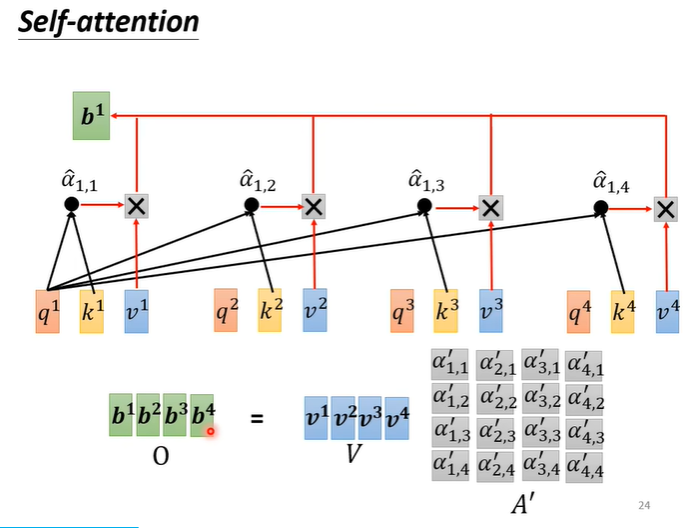
最后将矩阵V与矩阵相乘，即可得出由所有输出b组成的矩阵O。

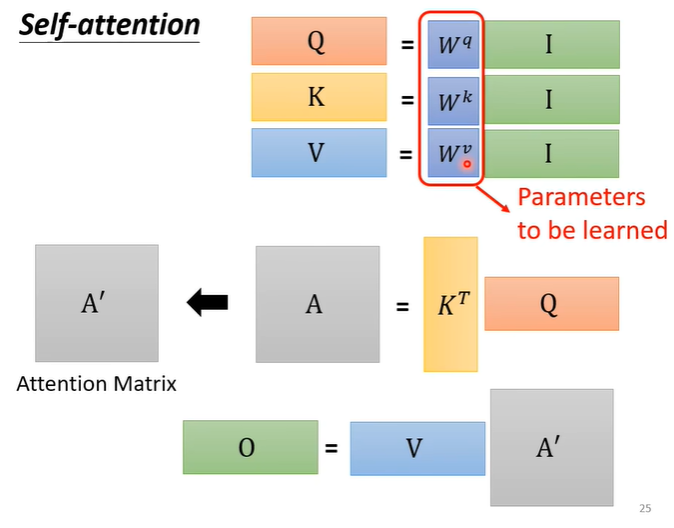
整个过程虽然看着很复杂，但是只有是需要训练的参数

2.Multi-head Self attention

Self attention还有一个进阶的版本叫Multi-head Self attention，需要多少head也是一个我们需要训练的一个参数，为什么我们会需要较多的head呢？因为相关这种事情有很多不同的形式，在Self attention中我们用q找相关的k，也许我们不能只有一个q，不同的q负责不同的相关性。

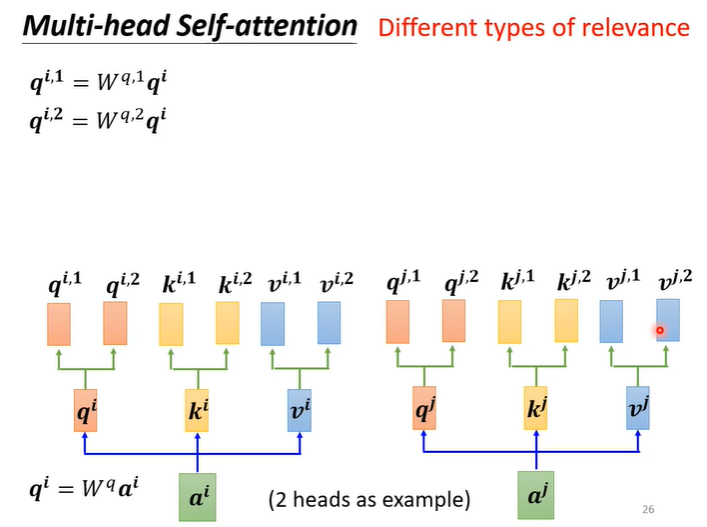
在原有的基础上，让q,k,v乘上两个不同的矩阵让q,k,v化为两组不同的q1,k1,v1和q2,k2,v2。对于其他位置也是同样的操作。

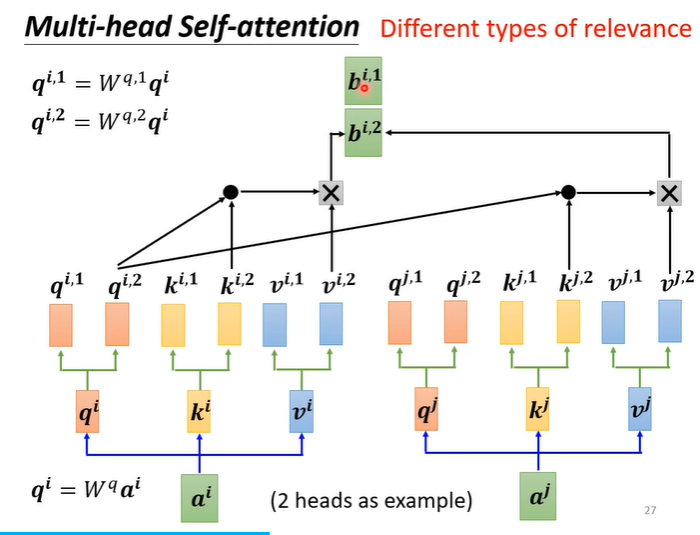
此时的Self attention的计算，让1组的q1,k1,v1一起做，二组的q2,k2,v2一起做。

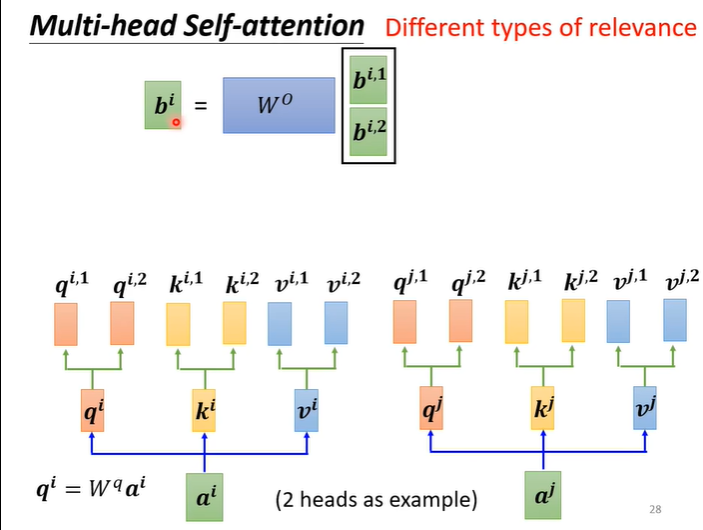
最后将两组得到b1和b2接起来通过一个transformer得到最终的b。

3.Positional encoding

在Self attention中，我们并没有任何相关的位置资讯，有时位置可能会很重要，例如词性标注时，动词不太会出现在句首等，如果我们想在Self attention中加入位置资讯，就要用到Positional encoding。

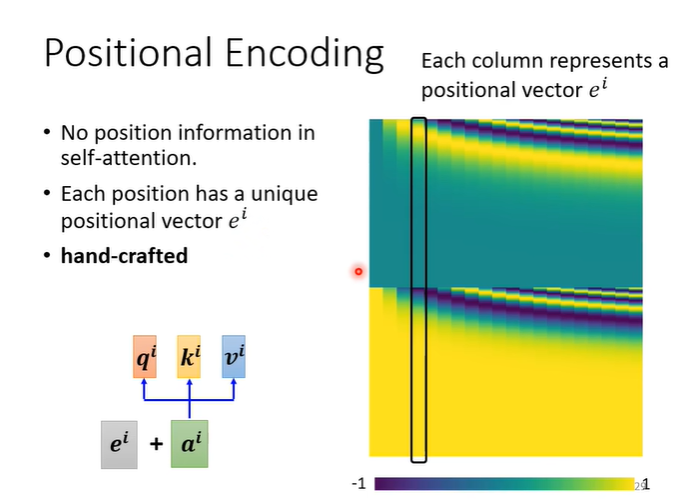
我们需要为每一个位置设定一个向量叫做positional vector，用表示，我们将e向量加入到a向量中即可。目前Positional encoding仍是尚待研究的问题，右侧的图片是初始的Positional encoding，每一个矩形代表一个位置。

4.Truncated self attention

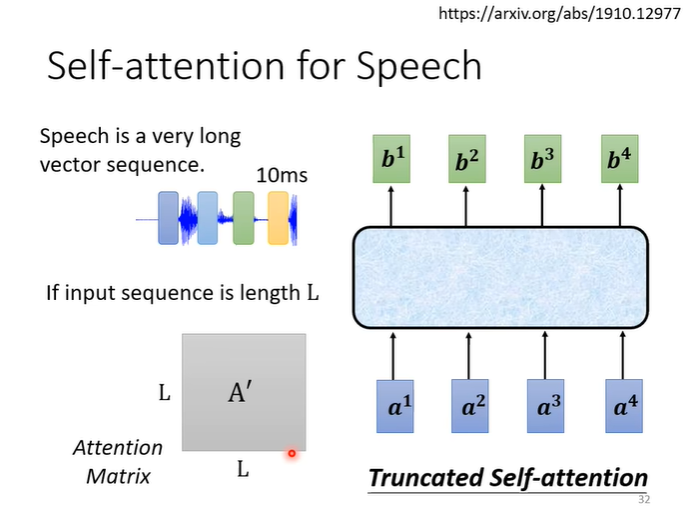
self attention也可以用于语音辨识，但是有一个问题就是，一个向量能表示的语音非常短，一秒的语音可能要100个向量，这会导致相关性矩阵非常大，不仅计算量很大，存储也需要很大的空间。所以就有了Truncated self attention，在做语音辨识的时候不看整句话，看部分即可，范围由自己设定。