【算法】——动态规划之路径问题
目录
前言:
一、不同路径
二、不同路径(Ⅱ)
三、下降最小路径和
四、地下城游戏
总结:
前言:
动态规划的主要问题是状态表示和状态转移方程,而这两个步骤除了方法以外还需要经验的支撑,所以多刷题是很有必要的。那么今天我们来看一个动态规划中的路径问题。
路径问题与之前基础动态规划问题的区别主要在于二维dp数组。
一、不同路径

题目中给出了一个m*n的网格,然后让我们计算从左上角走到右下角一共有多少种不同路径。
1. 由于这是个二维表格(与之前一维不同),所以我们需要定义二维dp表,这样才能方便地对每一个位置表示,定义dp[ i ][ j ]表示走到[ i ][ j ]位置为止,一共有的路径数量。
2. 根据题目可知,我们只能向右或向下走,所以要走到[ i ][ j ]位置的话只可能从[ i - 1 ][ j ]或者是[ i ][ j - 1 ]这两个前置位置,那么dp[ i ][ j ]的值应该是这两个位置路径数量之和。可知状态转移方程为:dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - 1 ]
3. 由状态转移方程可知dp[ i ][ j ]要用到左和上两个值,但第一排没有上面的值,第一列没有左边的值,为了方便统一使用状态转移方程,我们可以在最左和最上多申请一列,并初始化为0,这样就不会有越界访问的问题。而开始位置应该初始化为1,所以可以在多开的空间放一个1。(也可以不多开空间,单独对第一行和第一列分别初始化,但有些时候会比较麻烦,所以需要掌握这个技巧)
注意:动态规划中常会多开空间以方便初始化,但要对多开的空间进行合理初始化,来保证对整个过程没有影响
示例代码:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1, vector<int>(n+1));// 创建一个二维dp表,多生成一行一列,便于遍历// dp[i][j]表示到dp[i][j]为止,一共有的路径数dp[0][1] = 1;//初始化for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];}}return dp[m][n];}
};二、不同路径(Ⅱ)
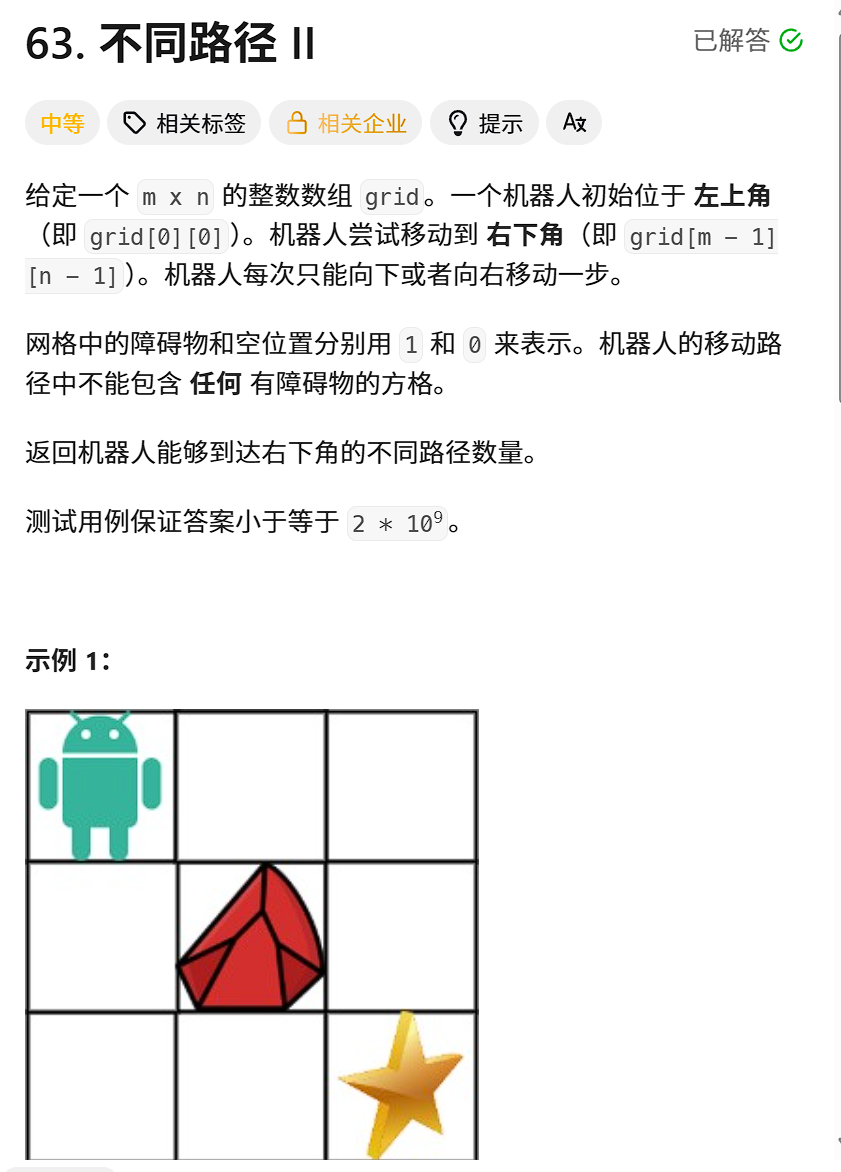
这题与上一题的区别是多了障碍物,那么我们该怎么处理这个障碍物呢?
因为有障碍物的地点是到达不了的,所以有障碍物的坐标dp值应该置为0,而对于状态转移方程实际是没有影响的,因为dp[ i ][ j ]在障碍物右边或下面时,相当于加了一个0。所以状态转移方程可以加一个if判断条件。
示例代码:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& ob) {int m = ob.size();int n = ob[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1));dp[0][1] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){// 没有障碍物if(ob[i-1][j-1] == 0){dp[i][j] = dp[i-1][j] + dp[i][j-1];}else{dp[i][j] = 0;}}}return dp[m][n];}
};三、下降最小路径和

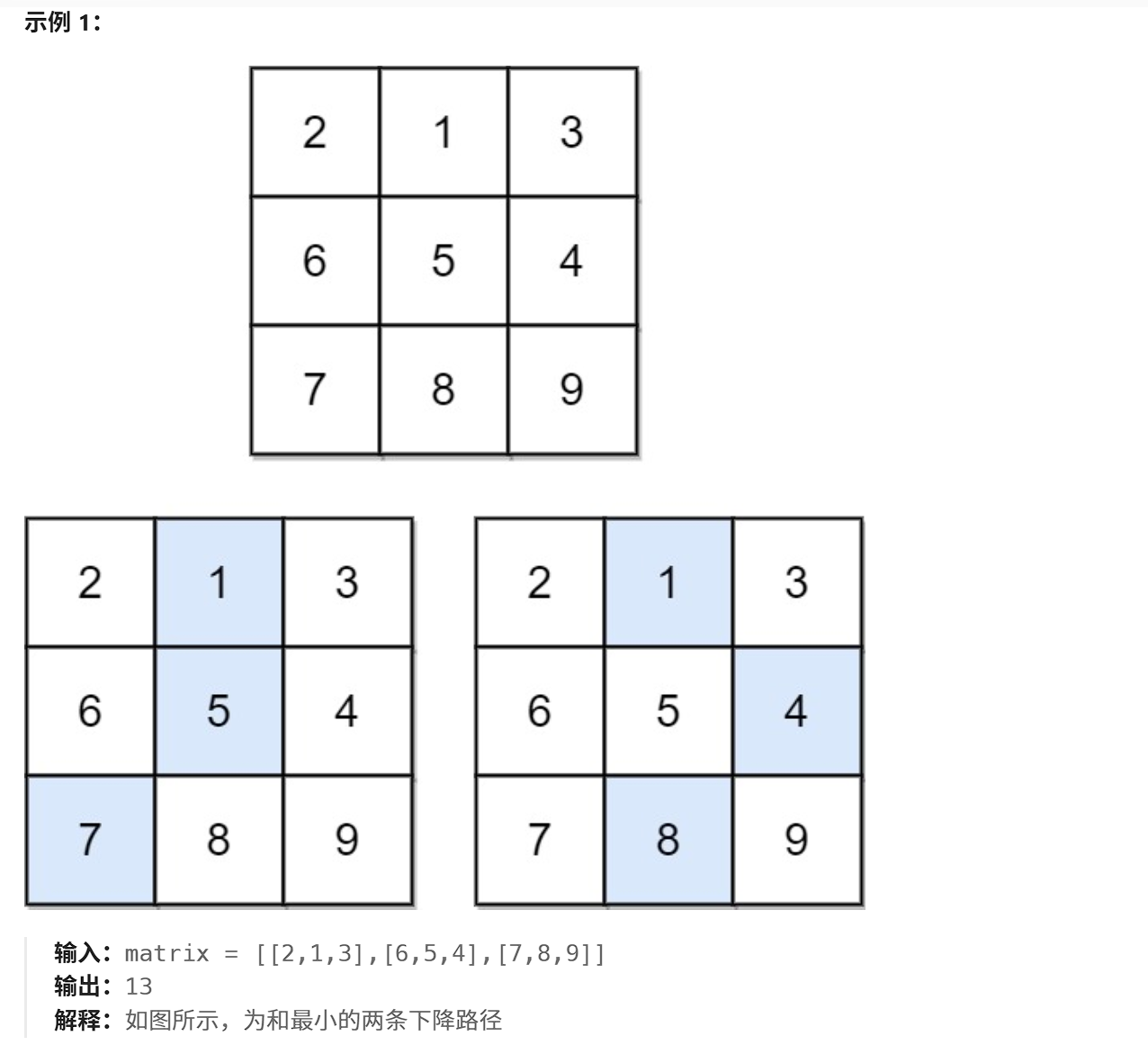
这道题要求下降最小路径和,即每次移动在垂直方向上都要下降一步,并且在水平方向上可以选择左右移动一步或不动。
1. 我们可以创建一个n * n的dp表,dp[ i ][ j ]表示走到[ i ][ j ]位置时,最小的下降路径和
2. 而dp[ i ][ j ]的值就等于,在上一排的左中右三个位置中选出一个最小值,也就是dp[ i-1 ][ j-1 ]、dp[ i-1 ][ j ]、dp[ i-1 ][ j+1 ]这三个位置,然后再加上[ i ][ j ]本身需要花费的值。所以状态转移方程为:dp[ i ][ j ] = min(min(dp[ i-1 ][ j-1 ], dp[ i-1 ][ j ]), dp[ i-1 ][ j+1 ]) + matrix[ i ][ j ]
3. 第一排初始化成matrix数组第一排的值即可。最左和最右两排比较特殊,只有两个值,可以选择多两排并初始化为一个最大值,但本次博主使用的是对这两排进行单独处理的方法。
示例代码:
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> dp(n, vector<int>(n));// dp[i][j]表示走到dp[i][j]位置为止的路径最小和// 初始化第一排for(int i = 0; i < n; i++){dp[0][i] = matrix[0][i];}for(int i = 1; i < n; i++){for(int j = 0; j < n; j++){if(j == 0){dp[i][j] = min(dp[i-1][j], dp[i-1][j+1]) + matrix[i][j];}else if(j < n-1){dp[i][j] = min(min(dp[i-1][j-1], dp[i-1][j]), dp[i-1][j+1]) + matrix[i][j];}else{dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + matrix[i][j];}}}int min = dp[n-1][0];for(int i = 1; i < n; i++){if(dp[n-1][i] < min){min = dp[n-1][i];}}return min;}
};四、地下城游戏

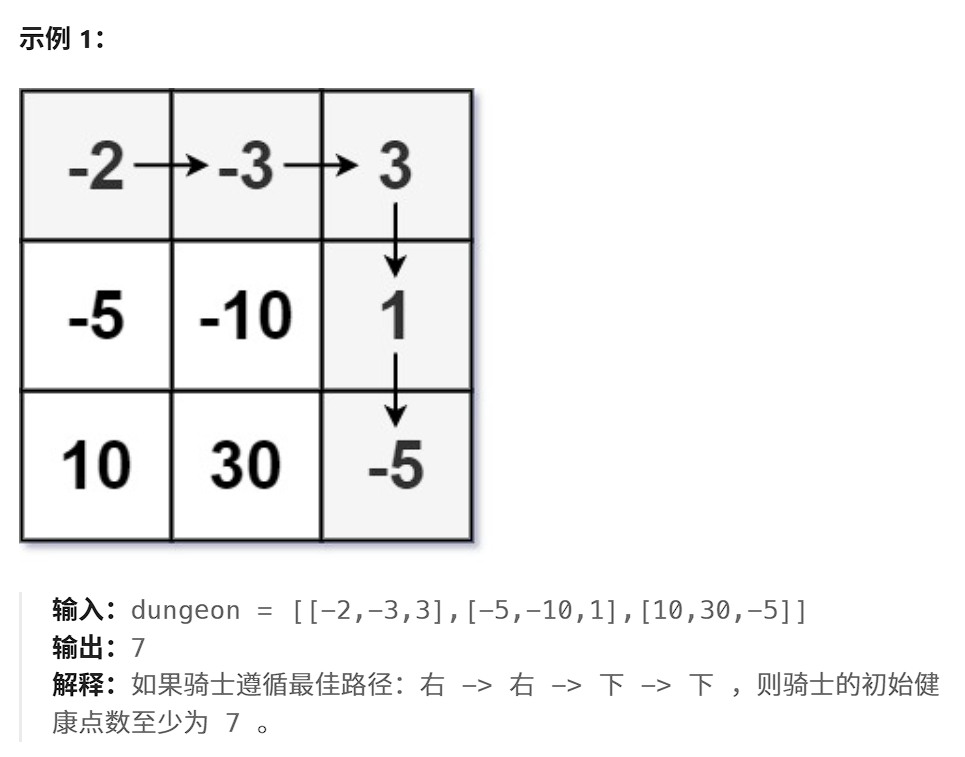
1. 这是本篇文章最难的一题,你会发现,如果按照常规的dp[ i ][ j ]表示到什么什么位置为止......很难解决问题,因为你无法确定开始时骑士需要的健康值。所以我们可以反过来,从终点开始往起点推,也就是从dp[ i ][ j ]表示从[ i ][ j ]为起点,到达终点所需的最低初始健康值。
2. 那么我们就可以反过来推,从dp[ i ][ j ]往起点走一步,那么他的最低健康值应该再减去那一步所需花费的健康值。又因为可以选择向右走或向下走,我们应该选择更小的那个,所以状态转移方程应该为:dp[ i ][ j ] = min(dp[ i+1 ][ j ], dp[ i ][ j+1 ]) - dungeon[ i ][ j ]。但数组中有正值,所以dp[ i ][ j ]减完可能为负数,但根据题目情况应保证他至少为1,所以还要加上:dp[ i ][ j ] = max(1, dp[ i ][ j ]);
3. 初始化可以在最又方和最下方多加一行一列,初始化为最大值,并在dp[ n ][ m-1 ]或dp[ n-1 ][ m ]赋值为1,表示到达终点后的健康值应为1。
示例代码:
class Solution {
public:int calculateMinimumHP(vector<vector<int>>& dungeon) {int m = dungeon.size();int n = dungeon[0].size();// dp[i][j]表示[i][j]位置开始,到达目标位置所需的最低初始健康点数vector<vector<int>> dp(m+1, vector<int>(n+1, INT_MAX));dp[m-1][n] = dp[m][n-1] = 1;for(int i = m-1; i >= 0; i--){for(int j = n-1; j >= 0; j--){dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j];dp[i][j] = max(1, dp[i][j]);// 最低健康值应至少为1}}return dp[0][0];}
};总结:
以上便是本文的所有内容了,如果觉得有帮助的话可以点赞收藏加关注支持一下!
