当前位置：首页 > news >正文

网站seo快速优化技巧jsp网站开发实例与发布

news 2025/10/12 5:06:11

网站seo快速优化技巧,jsp网站开发实例与发布,建筑公司愿景口号大全,网站建设工作室拍照线性回归作为统计学与机器学习领域中最基础且最重要的算法之一，其应用广泛且深远。它不仅是回归分析的入门方法，更是后续复杂模型构建的重要理论基础。理解线性回归算法的本质，既有助于提升数据分析的能力，也能为掌握更复杂的机器…

线性回归作为统计学与机器学习领域中最基础且最重要的算法之一，其应用广泛且深远。它不仅是回归分析的入门方法，更是后续复杂模型构建的重要理论基础。理解线性回归算法的本质，既有助于提升数据分析的能力，也能为掌握更复杂的机器学习算法打下坚实基础。尽管线性回归算法看似简单，其背后蕴含的数学原理、统计假设以及实际应用的复杂性，却值得深入探究。

线性回归的核心思想是通过构建变量之间的线性关系模型，揭示自变量与因变量之间的关系规律，进而实现对未知数据的预测和解释。这一方法基于经典的最小二乘估计思想，通过拟合样本数据点，使模型预测值与真实值之间的误差最小化。这里的“线性”不仅指变量间的关系形式，也体现为模型结构的简单性，便于解析和计算。

在数据科学不断发展、复杂算法层出不穷的时代，线性回归依然具有不可替代的价值。它是理解参数估计、模型评估与假设检验的核心起点。透过线性回归的框架，我们能够系统地理解模型的可解释性、泛化能力以及模型复杂度之间的权衡，这些都是构建稳健预测模型的重要议题。

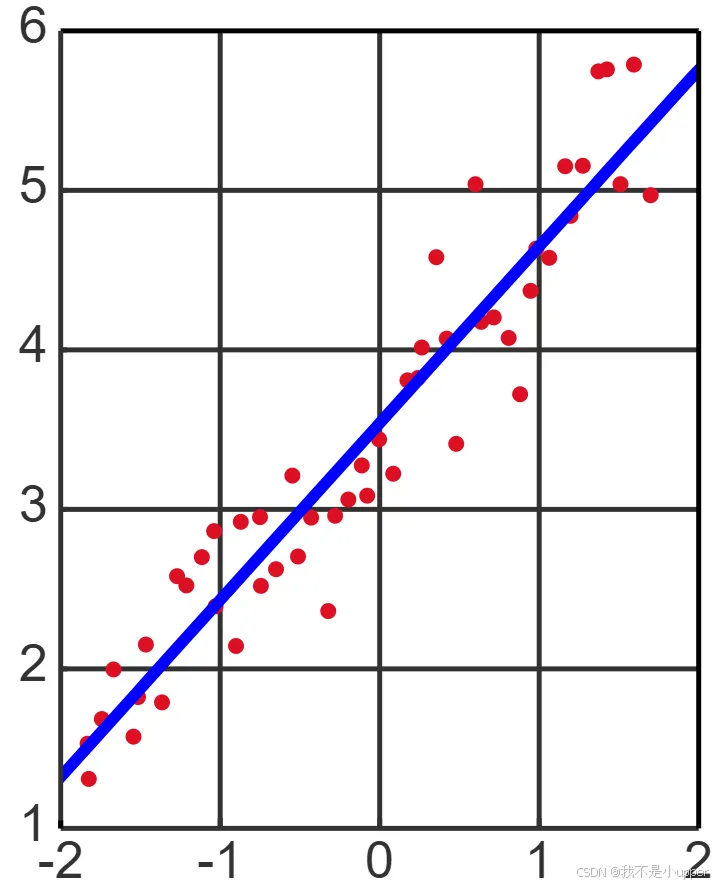
线性回归是一种用于刻画因变量与自变量之间线性关联的统计方法，其核心是通过数学模型量化这种关系。从形式上看，线性回归的一般表达式为：

$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \dots + \beta_kx_k + \varepsilon$ ，

其中y为因变量， $x_1, x_2, \dots, x_k$ 为自变量， $\beta_0$ 是截距项， $\beta_1, \dots, \beta_k$ 是对应自变量的回归系数（反映自变量对y的影响强度）， $\varepsilon$ 则为误差项，代表模型无法解释的随机波动。建模的目标是找到最优参数 $\beta_0, \beta_1, \dots, \beta_k$ ，使得模型的预测值 $\hat{y} = \beta_0 + \beta_1x_1 + \dots + \beta_kx_k$ 尽可能接近真实观测值y，这一过程通常通过最小二乘法实现 —— 即最小化平方残差和：

$\sum_{i=1}^n (y_i - \hat{y}_i)^2$ 。

为保证模型的有效性与推断合理性，线性回归对误差项$\varepsilon$有严格的统计假设：首先，误差项的均值必须为零（ $E[\varepsilon] = 0$ ），确保模型预测无系统偏差；其次，误差项需满足同方差性（ $Var(\varepsilon) = \sigma^2$ ， $\sigma$ 为常数），即误差的离散程度不随自变量变化；同时，误差项之间需相互独立（ $Cov(\varepsilon_i, \varepsilon_j) = 0$ ， $i \neq j$ ），避免序列相关导致的估计偏误；此外，误差项需服从正态分布（ $\varepsilon \sim N(0, \sigma^2)$ ），这是后续假设检验与置信区间构造的基础；最后，自变量之间不能存在完全线性相关（即无多重共线性），以保证参数估计的唯一性。这些假设是线性回归推断的理论基石，若被违反，可能导致参数估计偏差或模型解释力下降，因此检验假设是否成立是分析过程的关键环节。

参数估计的核心是最小二乘法（OLS），从矩阵视角可更清晰推导其过程。设自变量矩阵为

$X = \begin{bmatrix} 1 & x_{11} & \dots & x_{1k} \\ 1 & x_{21} & \dots & x_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \dots & x_{nk} \end{bmatrix}$ （第一列全为 1 对应截距项），

因变量向量为 $y = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}$ ，参数向量为 $\beta = \begin{bmatrix} \beta_0 \\ \beta_1 \\ \vdots \\ \beta_k \end{bmatrix}$ ，则残差平方和可表示为 $(y - X\beta)^T(y - X\beta)$ 。对 $\beta$ 求导并令导数为零，可得正规方程： $X^TX\beta = X^Ty$ ，若 $X^TX$ 可逆，则参数估计为 $\hat{\beta} = (X^TX)^{-1}X^Ty$ 。这一解析解具有无偏性、有效性等优良性质，若 $X^TX$ 不可逆（如存在多重共线性），则需通过奇异值分解（SVD）等数值方法求解。

模型训练完成后，需通过性能指标评估拟合效果。残差平方和（RSS）是基础指标：

$RSS = \sum_{i=1}^n (y_i - \hat{y}_i)^2$ ，其值越小说明拟合越好；决定系数 $R^2$ 更直观，公式为:

$R^2 = 1 - \frac{RSS}{TSS}$ （其中 $TSS = \sum_{i=1}^n (y_i - \bar{y})^2$ 为总平方和），反映模型解释因变量变异的比例，取值范围为 [0,1]，越接近 1 拟合越优；均方误差（MSE） $\text{MSE} = \frac{1}{n}\sum_{i=1}^n (y_i - \hat{y}_i)^2$ 衡量平均预测误差；均方根误差（RMSE） $\text{RMSE} = \sqrt{\text{MSE}}$ 则将误差转换为与因变量同量纲的指标，便于实际解读。实际应用中需结合多项指标综合评估，避免单一指标的局限性。

线性回归的适用存在一定限制：首先，它严格依赖因变量与自变量的线性关系，若实际关系为非线性（如二次、指数关系），模型拟合效果会显著下降；其次，模型对异常值敏感，极端数据点可能大幅扭曲参数估计，影响预测稳定性；此外，自变量间的多重共线性会导致参数估计方差增大，使结果不稳定且难以解释；最后，若误差项的正态性或同方差性假设不满足，传统的 t 检验、F 检验等推断结果可能失效。因此，数据预处理（如缺失值处理、异常值检测）、变量筛选与假设检验是确保模型有效的必要步骤。

从数据到应用，线性回归的实际流程可概括为：首先进行数据收集与清洗，确保数据质量（如处理缺失值、修正异常值）；其次是特征选择与工程，筛选相关自变量，必要时进行归一化、标准化或构造新特征（如交互项）；然后通过最小二乘法训练模型，求解回归系数；接着进行模型诊断，分析残差分布以检验假设（如残差是否正态、是否存在异方差）；之后计算 $R^2$ 、MSE 等指标评估性能；最后将模型应用于新数据进行预测。这一流程形成从理论到实践的闭环，强调数据质量与统计假设对结果的决定性影响。

为防止过拟合、提升模型泛化能力，线性回归常引入正则化方法，通过在目标函数中添加惩罚项约束参数复杂度。岭回归（L2 正则化）的目标函数为 $\sum_{i=1}^n (y_i - \hat{y}_i)^2 + \lambda\sum_{j=1}^k \beta_j^2$ （ $\lambda \geq$ 0为惩罚强度），可减小参数估计的方差，尤其在多重共线性严重时效果显著；Lasso 回归（L1 正则化）则采用绝对值惩罚：

$\sum_{i=1}^n (y_i - \hat{y}_i)^2 + \lambda\sum_{j=1}^k |\beta_j|$ ，

能将部分参数压缩至零，实现变量自动筛选，适合构建稀疏模型。两种方法均通过调节 $\lambda$ 平衡偏差与方差，实际中需通过交叉验证选择最优惩罚参数。

线性回归既是传统统计学工具，也是机器学习中基础的监督学习算法，二者虽形式相似但侧重点不同：统计学视角强调模型假设、参数推断（如通过 t 检验判断系数显著性），关注自变量对因变量的解释机制；机器学习视角则更注重预测性能，强调模型在未知数据上的泛化能力，常结合正则化、梯度下降等优化手段处理大规模数据与高维特征。例如，当数据量极大时，传统正规方程求解效率低下，此时迭代优化算法更适用 —— 梯度下降通过不断沿目标函数负梯度方向更新参数 $\beta = \beta - \alpha\nabla J(\beta)$ ， $\alpha$ 为学习率， $J(\beta)$ 为损失函数）；随机梯度下降（SGD）每次用单个样本计算梯度，加快迭代速度；批量梯度下降（Batch GD）用全部数据计算梯度，收敛更稳定；小批量梯度下降（Mini-batch GD）则折中两者，兼顾效率与稳定性，这些算法拓展了线性回归在现代大数据场景中的适用性。

模型中自变量的选择直接影响性能，常用方法包括：全子集回归尝试所有变量组合，选择拟合最优者，但计算成本极高；逐步回归通过前向选择（从无变量开始逐步添加）、后向剔除（从全变量开始逐步移除）或双向淘汰动态调整变量，平衡效率与效果；惩罚回归（如 Lasso）则通过正则化自动实现变量筛选，适合高维数据。合理选择变量可避免过拟合，提升模型的解释力与泛化能力。

线性回归的性能本质上受偏差与方差权衡影响：偏差是模型预测与真实值的系统偏离，方差是模型对训练数据波动的敏感程度。线性回归作为低复杂度模型，通常偏差较高、方差较低；增加模型复杂度（如引入高阶项）可降低偏差但可能增大方差，而正则化则通过约束复杂度实现偏差与方差的平衡，最终提升泛化能力。

综上，线性回归融合了数学严谨性与应用实用性，其核心是通过线性模型刻画变量关系，依赖严格的统计假设保证推断有效性，借助最小二乘法与正则化等方法优化参数，并通过系统的评估与诊断确保模型稳健性。即便在复杂模型层出不穷的今天，线性回归依然是数据分析的基础工具，深入理解其原理与应用边界，对构建科学的分析体系至关重要。

查看全文

http://www.dtcms.com/a/469000.html