【每日算法C#】x 的平方根 LeetCode

国庆假期结束，冲！

1. 方法对比：二分查找法 vs 牛顿迭代法

(1) 二分查找法

public int MySqrt(int x)
{if (x == 0) return 0;int left = 1;int right = x;while (left <= right){int mid = left + (right - left) / 2;long square = (long)mid * mid;if (square == x)return mid;else if (square < x)left = mid + 1;elseright = mid - 1;}return right;
}

(2) 牛顿迭代法

public int MySqrt(int x)
{if (x == 0) return 0;long r = x;while (r * r > x)r = (r + x / r) / 2;return (int)r;
}

2. 对比分析

特性	二分查找法	牛顿迭代法
时间复杂度	O(log n)	O(log log n)（二次收敛）
迭代次数	最多约31次（对于int范围）	通常少于10次（对于int范围）
收敛速度	线性收敛	二次收敛（指数级加速）
实现难度	较简单	更简洁
内存占用	需要维护左右边界	只需单个变量
适用场景	通用查找算法	数值计算优化
精度控制	精确整数解	精确整数解

3. 牛顿迭代法的由来与数学原理

(1) 历史背景

牛顿迭代法由英国科学家艾萨克·牛顿在17世纪提出，最初用于求解多项式方程的根。约瑟夫·拉弗森在1690年将其推广，因此也称为牛顿-拉弗森方法。

(2) 数学推导

求解平方根等价于求方程：
f(r) = r² - x = 0 的根

使用泰勒级数一阶展开：

解得：

代入 f(r) = r² - x 和 f'(r) = 2r：

更新公式：

简化后得到：

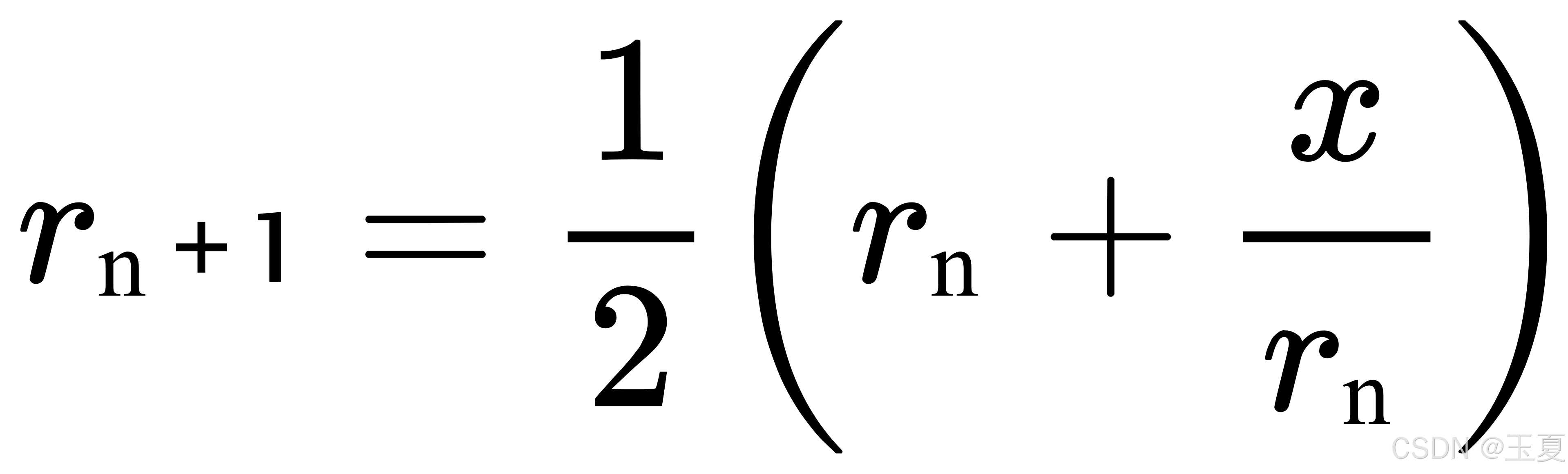
(3) 几何解释

牛顿法本质是切线逼近法：

1. 在曲线上任选一点 (rₙ, f(rₙ))
2. 作该点的切线
3. 切线与x轴的交点作为新估计值 rₙ₊₁
4. 重复直到收敛

4. 为什么牛顿法更快？

1. 超线性收敛：误差 eₙ₊₁ ≈ (1/2)eₙ²
2. 自适应步长：远离目标时步长大，接近目标时步长小
3. 利用导数信息：通过斜率预测更优解

5. 注意事项

1. 初始值选择：牛顿法对初始值敏感（但平方根问题中取 x 是安全的）
2. 整数除法：在整数运算中 x/r 会截断，但不影响最终结果
3. 边界处理：x=0 需要单独处理（两种方法都做了）

6. 总结

方面	胜出方	原因
理论速度	牛顿迭代法	二次收敛 vs 线性收敛
代码简洁性	牛顿迭代法	5行 vs 10行
内存效率	牛顿迭代法	单变量 vs 多变量
可理解性	二分查找法	更直观
数值稳定性	平手	整数运算中表现相当

推荐选择：牛顿迭代法更优，尤其在大数计算中优势明显（如 x=2³¹-1 时，牛顿法只需约10次迭代，二分法需31次）