深度学习基础-Chapter 01-感知机和全连接

1 感知机

感知机（又称神经元）由 Frank Rosenblatt 于 1957 年提出，虽历史悠久但仍是学习神经网络与深度学习的基础。其核心思想是现代多层神经网络的起源，掌握感知机构造有助于理解深度学习的底层逻辑。

1.1 感知机是什么？

感知机接收多个输入信号，输出 1（传递信号）或 0（不传递信号）的二元结果，信号流动特性类似电流，但其取值仅两种状态。

接收两个输入信号的感知机中，输入信号 x1、x2 经权重 w1、w2 加权后求和，若总和超过阈值 θ，神经元激活并输出 1，否则输出 0，其中权重反映信号重要性，θ 为激活界限值。如下图所示。

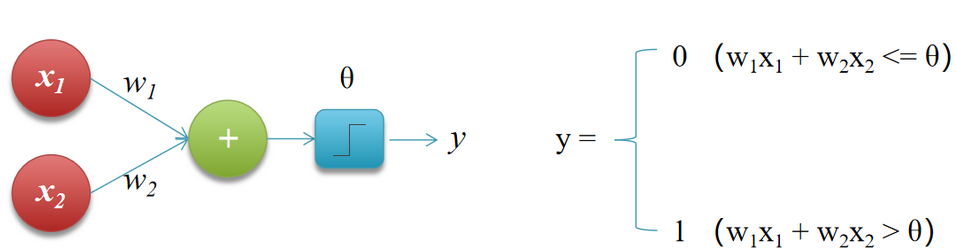
感知机中各输入信号的权重(w1,w2)控制其重要性，权重越大对应信号越重要。

1.2 感知机的简单应用

1.2.1 逻辑与

"与门"是一种二输入单输出的门电路，其真值表为：当且仅当两个输入均为 1 时输出 1，否则输出 0，逻辑与的真值表如下图所示。

1.2.2 逻辑或

“或门”是只要有一个输入信号是1，输出就为1，输入信号全 0 时输出 为0 的逻辑电路。逻辑或的真值表如下图所示。

1.2.3 逻辑与非

与非门就是颠倒了与门的输出，当且仅当两个输入均为 1 时输出 0，否则输出1，其真值表如下图所示。

1.3 感知机的实现

1.3.1 简单实现

def AND(x1, x2):w1, w2, theta = 0.5, 0.5, 0.7tmp = x1*w1 + x2*w2if tmp <= theta:return 0elif tmp > theta:return 1
if __name__ == "__main__":print(AND(0, 0)) #0print(AND(1, 0)) #0print(AND(0, 1)) #0print(AND(1, 1)) #1

1.3.2 使用权重和偏置的实现

刚才与门的实现比较直接、容易理解，但是考虑到以后的事情，将其修改为另外一种实现形式。将theta换成b，得到如下表达式：

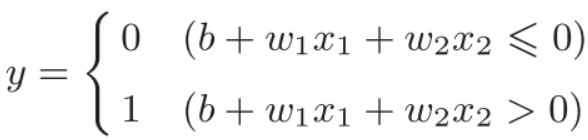
其中b称为偏置，w1和w2称为权重。感知机 会计算输入信号和权重的乘积，然后加上偏置，如果这个值大于0则输出1，否则输出0。

AND代码：

"""逻辑与/与门"""
import numpy as np# 定义AND函数，接收两个输入x1和x2
def AND(x1, x2):# 将输入转换为NumPy数组x = np.array([x1, x2])# 设置权重w = [0.5, 0.5]w = np.array([0.5, 0.5])# 设置偏置b = -0.7b = -0.7# 计算加权和加上偏置：w*x的点积 + btmp = np.sum(w * x) + b# 如果结果小于等于0，返回0if tmp <= 0:return 0# 否则返回1elif tmp > 0:return 1if __name__ == '__main__':print(AND(0, 0))  # 0print(AND(1, 0))  # 0print(AND(0, 1))  # 0print(AND(1, 1))  # 1

OR代码：

"""逻辑或/或门"""
"""逻辑与非/与非门"""
# 导入NumPy库，用于数值计算
import numpy as np# 定义OR函数，接收两个输入x1和x2
def OR(x1, x2):# 将输入转换为NumPy数组x = np.array([x1, x2])# 设置权重w = [0.5, 0.5]（与AND门相同）w = np.array([0.5, 0.5])# 设置偏置b = -0.2（与AND门不同，使用负值）b = -0.2# 计算加权和加上偏置：w*x的点积 + btmp = np.sum(w * x) + b# 如果结果小于等于0，返回0if tmp <= 0:return 0# 否则返回1else:return 1if __name__ == '__main__':print(OR(0, 0))  # 0print(OR(1, 0))  # 1print(OR(0, 1))  # 1print(OR(1, 1))  # 1

NAND代码：

"""逻辑与非/与非门"""
# 导入NumPy库，用于数值计算
import numpy as np# 定义NAND函数，接收两个输入x1和x2
def NAND(x1, x2):# 将输入转换为NumPy数组x = np.array([x1, x2])# 设置权重w = [-0.5, -0.5]（负的AND权重）w = np.array([-0.5, -0.5])# 设置偏置b = 0.7b = 0.7# 计算加权和加上偏置：w*x的点积 + btmp = np.sum(w * x) + b# 如果结果小于等于0，返回0if tmp <= 0:return 0# 否则返回1else:return 1if __name__ == '__main__':print(NAND(0, 0))  # 1print(NAND(1, 0))  # 1print(NAND(0, 1))  # 1print(NAND(1, 1))  # 0

小结：权重 w1、w2 控制输入信号重要性，偏置 b 调整神经元激活难易度（如 b=-0.1 时加权和超 0.1 激活，b=-20.0 时需超 20.0）。与门、与非门、或门的感知机构造相同，仅权重和偏置取值不同。

1.4 感知机的局限

感知机的核心瓶颈在于线性模型的先天缺陷和单层网络的结构限制。其局限性推动了神经网络的发展。

1.5 多层感知机

多层感知机（MLP，Multilayer Perceptron）也叫人工神经网络（ANN，Artificial Neural Network）除了输入输出层，它中间可以有多个隐层，最简单的MLP只含一个隐层，即三层的结构，如下图：

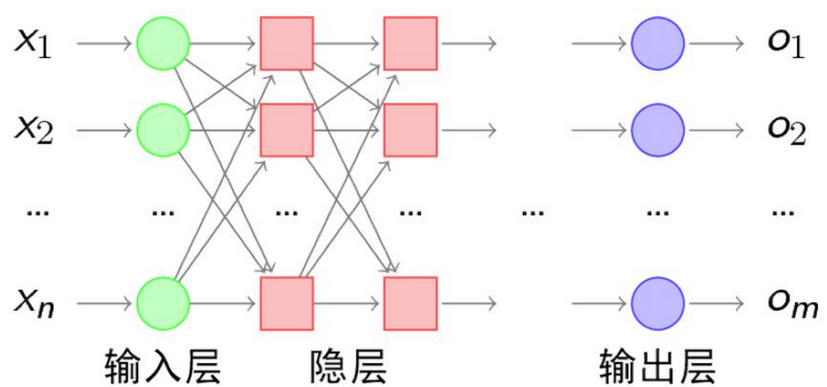
从上图可以看到，多层感知机层与层之间是全连接的。多层感知机包括三层：
输入层：接收原始特征（如图片像素、文本向量），节点数等于特征维度。
隐藏层：位于输入层和输出层之间，可包含一层或多层神经元。隐藏层神经元通过权重矩阵与前一层连接，是特征变换的核心
输出层：根据任务类型输出结果（如二分类输出 1 个节点，多分类输出 Softmax 层）

2 全连接与链式求导法则

2.1 全连接神经网络

全连接神经网络（Fully Connected Neural Network），中每个节点与下一层所有节点相连，通过调整节点连接关系处理信息，工程和学术界常简称其为 “神经网络”，如下图所示：

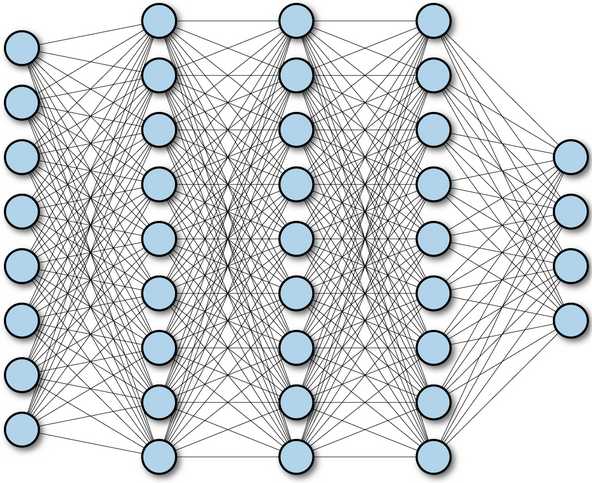
全连接神经网络通常包括输入层、隐藏层、输出层三层核心结构，每层由若干节点（神经元）组成，且层间节点全连接。如下图所示：

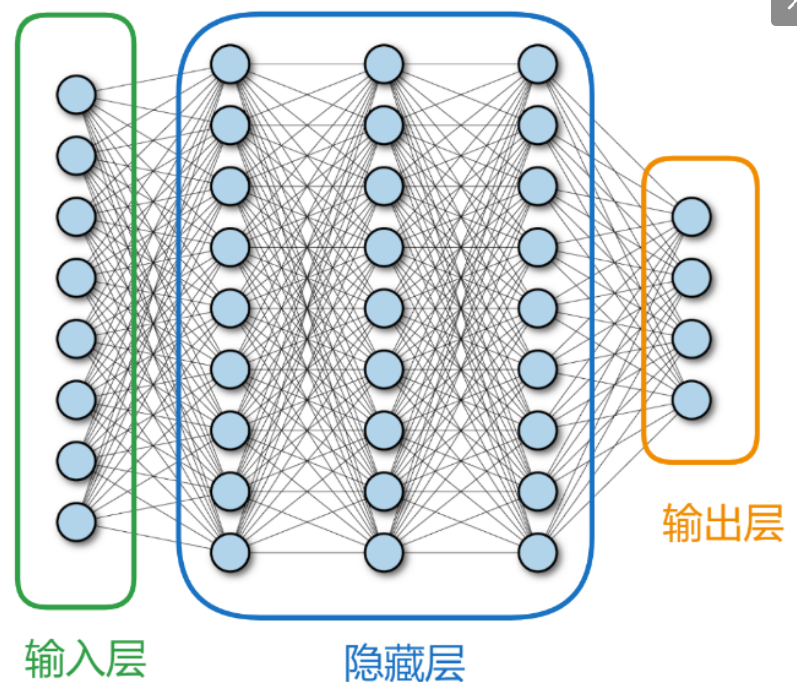
输入层

深度学习神经网络输入类型多样（数组，文字，图像、音频等），但对网络而言仅接收n维数据。输入层神经元数量增减需结合任务，须采用对逻辑回归或分类有实际意义的数据，训练才更有效。除数据有意义外，数据效率也关键，对样本进行算法加工（如图像灰度化）可助力网络训练。

隐藏层

全连接隐藏层是全连接神经网络的核心组成部分，位于输入层和输出层之间，负责对数据进行非线性特征提取与抽象。

输出层

全连接神经网络输出层神经元个数需根据任务类型灵活设置，如回归问题、分类问题等场景均需适配实际需求。

2.2 关于全连接与链式求导法则实验步骤

散点输入→前向计算→参数初始化→损失函数→开始迭代→反向传播→显示频率设置→梯度下降显示

2.2.1 散点输入

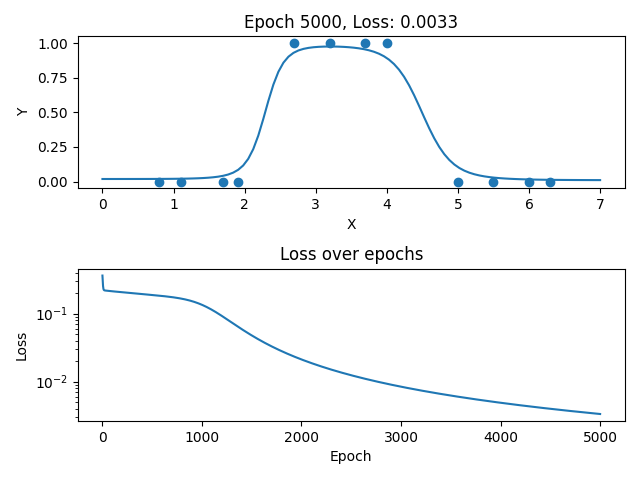
假如现在调查某人对衣服的尺码的接受程度，当衣服的尺码过大或者过小时，都穿不上。采集了某人对衣服尺码（横坐标）的接受程度（纵坐标），并且将它们绘制在一个二维坐标中，其分布如下图所示：
其坐标分别为：[0.8, 0]，[1.1, 0]，[1.7, 0]，[1.9, 0]，[2.7, 1]，[3.2, 1]，[3.7, 1]，[4.0, 1]，[5.0, 0]，[5.5, 0]，[6.0, 0]，[6.3, 0]，纵坐标1代表能穿上，0代表穿不上。

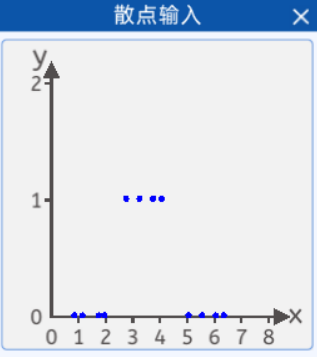
那么就可以搭建一个神经网络，将散点数据带入网络中进行训练，从而拟合出一条曲线，使该曲线能够尽可能准确的描述衣服尺码与被接受程度的关系，那样就可以预测某件衣服的不同尺码的被接受程度。

2.2.2 前向计算

神经网络，也称为人工神经网络（ANN）或模拟神经网络（SNN），是机器学习的子集，并且是深度学习算法的核心。其名称和结构是受人类大脑的启发，模仿了生物神经元信号相互传递的方式，但实际上并不十分相通。一般分为3个层次：输入层，隐藏层，输出层，下图就是一个最简单的神经网络结构。

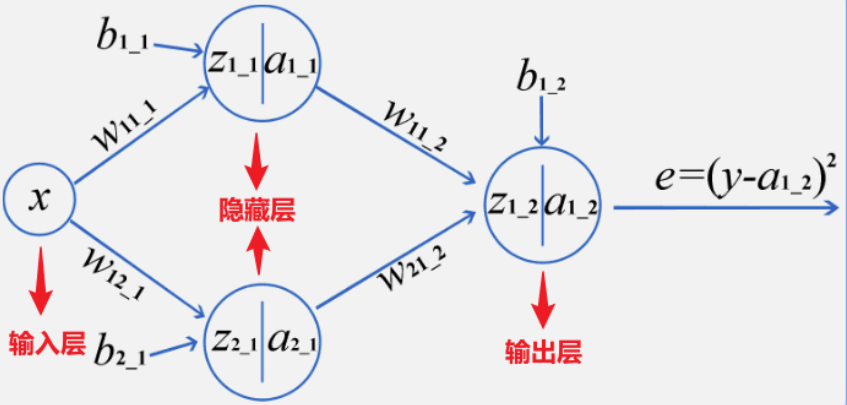
在上图中，所有的“圆圈”有一个共同的名字，叫做神经节点。一个神经网络是由很多个节点来构成的，不同层的节点会有不同的作用。

比如节点“x”所在的层叫做输入层。每个神经网络都只有一个输入层，但输入层可以有很多个“输入”节点，所有的特征都从该层进行输入。比如上面的神经网络中输入层只有“x”一个节点，也就意味着该神经网络只有一个输入特征，例如根据用水量判断水费，“x”就是用水量。

节点"a1_1"和节点"a2_1"所在的层叫做隐藏层，一个神经网络可以有很多个隐藏层，每一个隐藏层中也可以有很多个节点。

隐藏层是用来对输入的特征进行计算的结果，层数越多，模型越复杂。

从隐藏层开始，每个节点都是有计算公式的，包括输出层。计算公式为：

其中 y就是经过计算并激活的结果，对应上面的等节点；是激活函数，用于代入非线性因素，在本实验中用的是激活函数Sigmoid()

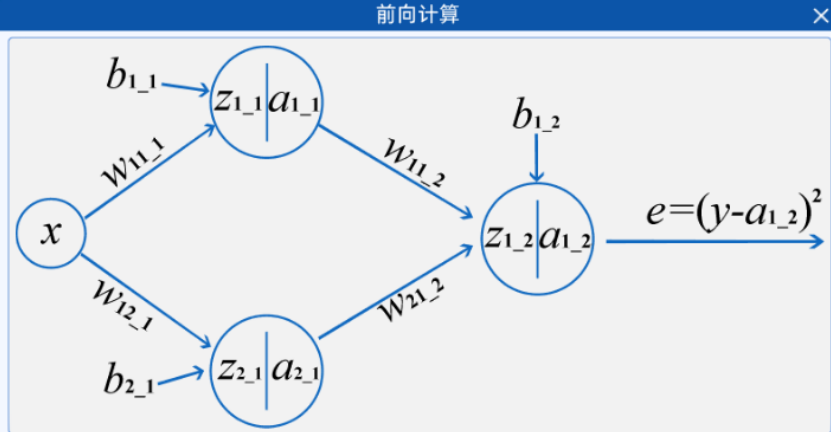
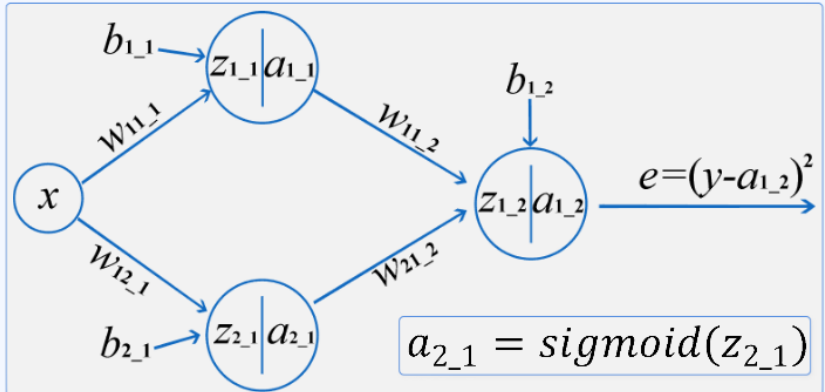
最后根据输出结果得到损失函数：这就是全连接神经网络中的前向计算的过程。

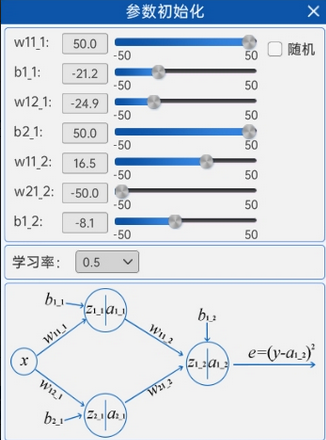
2.2.3 参数初始化

了解了全连接神经网络中的前向计算过程后，就可以进行前向计算了。首先要进行的就是参数初始化，在“参数初始化”组件中，可以修改神经网络计算过程中所涉及到的参数以及后续反向传播更新参数用到的学习率，并且随着参数的修改，原本的直线会随着参数的修改而改变形状。如下图所示：

2.2.4 损失函数

由于本实验的最终目标是拟合一条曲线，所以损失函数使用的还是MSE（均方误差损失函数）。

2.2.5 开始迭代

与机器学习一样，神经网络也是通过不断的迭代更新来训练参数的，不同的是，神经网络的模型结构会比机器学习复杂的多，其中所涉及到的参数量也远远大于机器学习，因此，神经网络的迭代次数一般都很大，同时，由于本实验的拟合线较复杂但是网络偏简单，所以并不是很好拟合。本实验中，“开始迭代”组件中默认选择的迭代次数是5000次。

2.2.6 反向传播

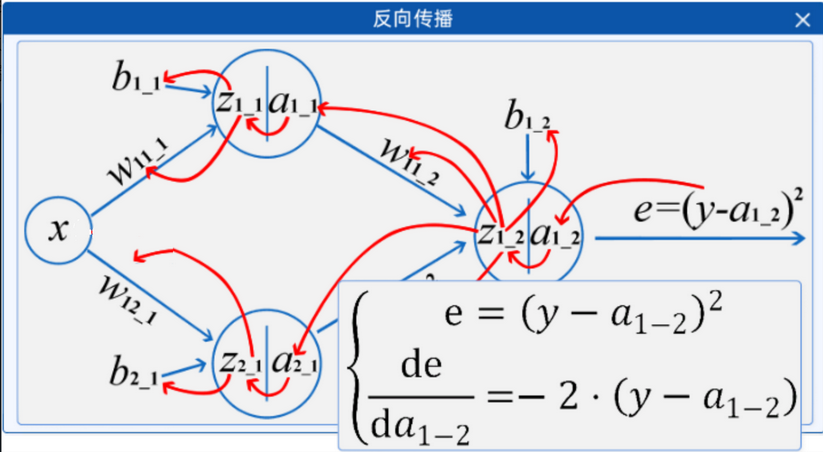
链式法则在计算神经网络中的梯度（反向传播）时非常重要，因为神经网络中的层与层之间通常是复合函数关系。通过链式法则，可以有效地计算损失函数对网络参数的梯度，从而进行梯度下降优化。

2.2.7 显示频率设置

2.2.8 梯度下降显示

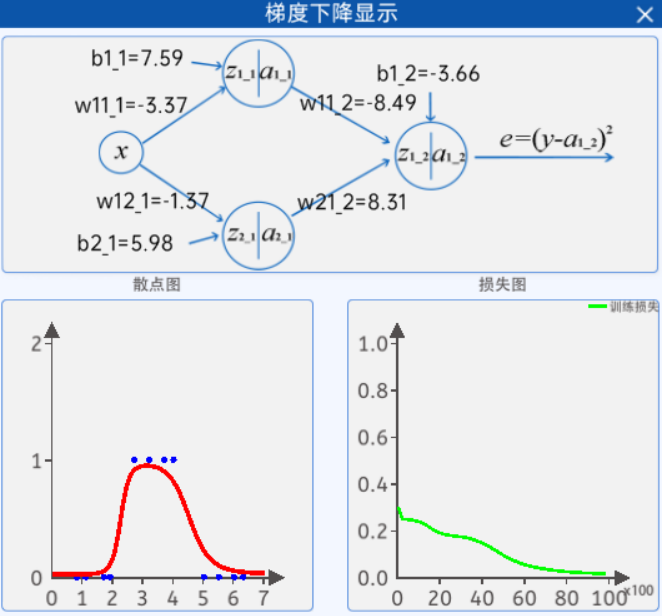
其中，每个参数的值都是随着神经网络的迭代而实时更新的。

而左边的图则是根据上面的参数值而实时绘制的图形，右边的图则是当前参数值下的损失值，随着迭代次数的不断增长，参数值在不断的更新，损失值也在不断的更新。

注意：随机参数由于网络比较简单但特征相对复杂导致可能会不拟合，建议在“参数初始化”组件中的初始化值使用上图中的参数。使用该参数过程类似于迁移学习，可得到一个较好的拟合结果。

代码：

"""
我们有一个两层神经网络，输入层只有一个特征，隐藏层有两个神经元，输出层有一个神经元。
目标：使用反向传播算法训练网络，对给定的点进行分类。实现了一个简单的两层神经网络，用于对给定的二维数据点进行分类。
网络包含一个隐藏层（2个神经元）和一个输出层（1个神经元），
使用sigmoid激活函数和均方误差损失函数，通过反向传播算法进行训练。
"""
# 1. 导入库和数据准备
import numpy as np
import matplotlib.pyplot as plt# 输入数据：第一列是特征值，第二列是标签(0或1)
points = np.array([[0.8, 0],[1.1, 0],[1.7, 0],[1.9, 0],[2.7, 1],[3.2, 1],[3.7, 1],[4.0, 1],[5.0, 0],[5.5, 0],[6.0, 0],[6.3, 0]])
# 分离特征与标签
X = points[:, 0]  # 特征值
Y = points[:, 1]  # 标签 - 修正这里：使用所有行的第二列
"""
这里我们有一组数据点，每个点有一个特征值(X)和一个二分类标签(Y)。
从数据分布可以看出，这是一个非线性可分的问题，需要神经网络来学习复杂的决策边界。
"""# 2. 前向传播函数
# sigmoid 函数
def sigmoid(x):  # 修正函数名拼写错误return 1 / (1 + np.exp(-x))def forward(w11_1, b1_1, w12_1, b2_1, w11_2, w21_2, b1_2, x):# 第一层第一个神经元的计算z1_1 = w11_1 * x + b1_1a1_1 = sigmoid(z1_1)# 第一层第二个神经元计算z2_1 = w12_1 * x + b2_1a2_1 = sigmoid(z2_1)# 第二层（输出层）的计算z1_2 = a1_1 * w11_2 + a2_1 * w21_2 + b1_2a1_2 = sigmoid(z1_2)return a1_1, a2_1, a1_2"""
前向传播过程：输入数据通过第一层的两个神经元每个神经元计算加权和并应用sigmoid激活函数第一层的输出作为第二层(输出层)的输入输出层计算最终结果
"""# 3.参数初始化和损失函数
# 参数初始化
w11_1, b1_1, w12_1, b2_1, w11_2, w21_2, b1_2 = 0.1, 0.6, 0.9, -1.5, 0.1, 0.9, 0.2
lr = 0.5  # 学习率# 损失函数（均方误差）
def loss_func(y, y_hat):loss = np.mean((y - y_hat) ** 2)return loss"""w11_1, w12_1: 输入到隐藏层的权重b1_1, b2_1: 隐藏层的偏置w11_2, w21_2: 隐藏层到输出层的权重b1_2: 输出层的偏置lr: 学习率，控制参数更新的步长
损失函数使用均方误差(Mean Squared Error)，衡量预测值与真实值之间的差异
"""# 画图用
x_values = np.linspace(0, 7, 100)
loss_list = []
epoches_list = []# 4.训练过程（反向传播）
epoches = 5000  # 迭代次数
for epoch in range(1, epoches + 1):# 前向传播计算输出和损失a1_1, a2_1, a1_2 = forward(w11_1, b1_1, w12_1, b2_1, w11_2, w21_2, b1_2, X)loss = loss_func(Y, a1_2)loss_list.append(loss)epoches_list.append(epoch)# 反向传播计算梯度# 输出层梯度计算deda1_2 = -2 * (Y - a1_2)  # 损失对输出层输出的导数dedz1_2 = deda1_2 * a1_2 * (1 - a1_2)  # 损失对输出层输入的导数# 输出层权重和偏置的梯度dedw11_2 = np.mean(dedz1_2 * a1_1)dedw21_2 = np.mean(dedz1_2 * a2_1)dedb1_2 = np.mean(dedz1_2)# 隐藏层梯度计算deda1_1 = dedz1_2 * w11_2  # 损失对隐藏层第一个神经元输出的导数dedz1_1 = deda1_1 * a1_1 * (1 - a1_1)  # 损失对隐藏层第一个神经元输入的导数# 隐藏层第一个神经元的权重和偏置的梯度dedw11_1 = np.mean(dedz1_1 * X)dedb1_1 = np.mean(dedz1_1)# 隐藏层第二个神经元的梯度计算deda2_1 = dedz1_2 * w21_2  # 损失对隐藏层第二个神经元输出的导数dedz2_1 = deda2_1 * a2_1 * (1 - a2_1)  # 损失对隐藏层第二个神经元输入的导数# 隐藏层第二个神经元的权重和偏置的梯度dedw12_1 = np.mean(dedz2_1 * X)dedb2_1 = np.mean(dedz2_1)# 梯度下降更新参数w11_2 = w11_2 - lr * dedw11_2w21_2 = w21_2 - lr * dedw21_2b1_2 = b1_2 - lr * dedb1_2w11_1 = w11_1 - lr * dedw11_1b1_1 = b1_1 - lr * dedb1_1w12_1 = w12_1 - lr * dedw12_1b2_1 = b2_1 - lr * dedb2_1"""反向传播过程：计算损失函数对输出层输出的导数计算损失函数对输出层输入的导数(使用链式法则)计算输出层权重和偏置的梯度计算隐藏层神经元的梯度(继续使用链式法则)计算隐藏层权重和偏置的梯度使用梯度下降法更新所有参数"""# 7.显示频率设置if epoch == 1 or epoch % 100 == 0:print(f"epoch:{epoch},loss:{loss}")# 画图 散点图及预测曲线# 清除当前图形plt.clf()plt.subplot(2, 1, 1)# 画Y的散点和拟合线a1_1, a2_1, a1_2 = forward(w11_1, b1_1, w12_1, b2_1, w11_2, w21_2, b1_2, x_values)plt.plot(x_values, a1_2)# 画散点plt.scatter(X, Y)plt.title(f'Epoch {epoch}, Loss: {loss:.4f}')plt.xlabel('X')plt.ylabel('Y')# 画损失值plt.subplot(2, 1, 2)plt.plot(epoches_list, loss_list)plt.title('Loss over epochs')plt.xlabel('Epoch')plt.ylabel('Loss')plt.yscale('log')  # 使用对数刻度更好地观察损失变化plt.tight_layout()plt.pause(0.1)# 8.梯度下降显示
plt.savefig('2.png')
plt.show()"""
神经网络的结构: 
输入层(1个神经元) → 隐藏层(2个神经元) → 输出层(1个神经元)学习过程1.前向传播：数据从输入层流向输出层，计算预测值2.计算损失：比较预测值与真实值3.反向传播：从输出层向输入层传播误差，计算各参数的梯度4.参数更新：使用梯度下降法调整参数，减小损失
通过多次迭代，神经网络逐渐学习到数据中的模式，损失函数值会逐渐减小。
"""

代码运行结果：2.png