算法4.0

11. 盛最多水的容器 - 力扣（LeetCode）

想简单了 审题时候补药着急  慢慢来 多试试几个例子

算法原理

解法1：暴力枚举    双层for循环  算出所有值然后找最大值（肯定超时的）

public class Solution {public int maxArea(int[] height){int maxArea = 0;for (int i = 0; i <height.length ; i++) {for (int j = i+1; j <height.length; j++) {//j从j+1开始 避免重复计算int h = Math.min(height[i],height[j] );int w = j-i;  //宽度int area = h*w;if(area >maxArea){maxArea = area;//更新最大值}}}return maxArea;}
}

解法2：  单调性  双指针

先找一个小区间研究

选择最边的两个   然后逐级向内  发现宽度一直在减小（永远都在减小）

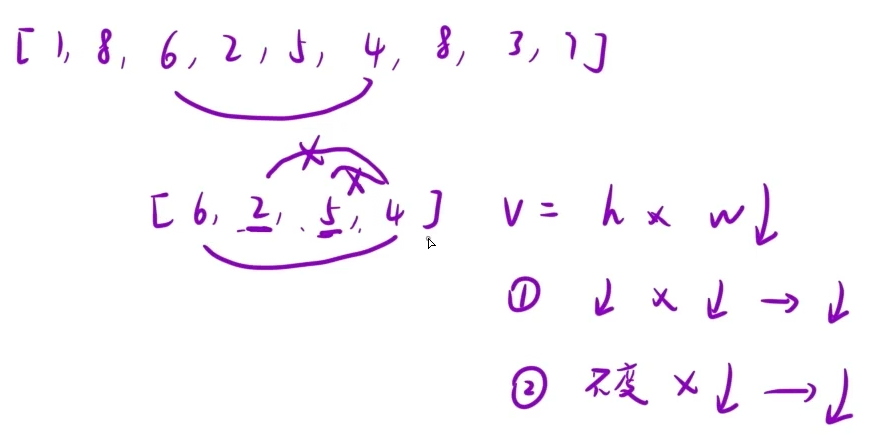
如果拿6 和 4计算完成之后  接下来用4和2计算 4和5计算 宽度永远在减小（向内枚举）

高度变化：如果向内枚举的时候 碰到了比我小的数   高度也减小  宽度也在减小（向内枚举） 

                  这个时候最终结果一定减小

                  如果向内枚举的时候  碰到了比我大的数  高度不变（最小的为水桶高度）  宽度在减小

                  这个时候最终结果一定减小

如果你的总体积是减小的  我要的是盛水最多的容器  那么中间2 和 5  就不需要枚举了

因为这个时候 最边的6和4就是记录的最大的容器   所以干掉4

规律扩大 

直接用题目给的数组开干  

用最左边和最右边先计算   计算完记录结果V1之后干掉左面（上面研究的那个例子证明一定减小）

第二部分直接干掉7   循环往复 慢慢干掉所有  下面是图片展示过程

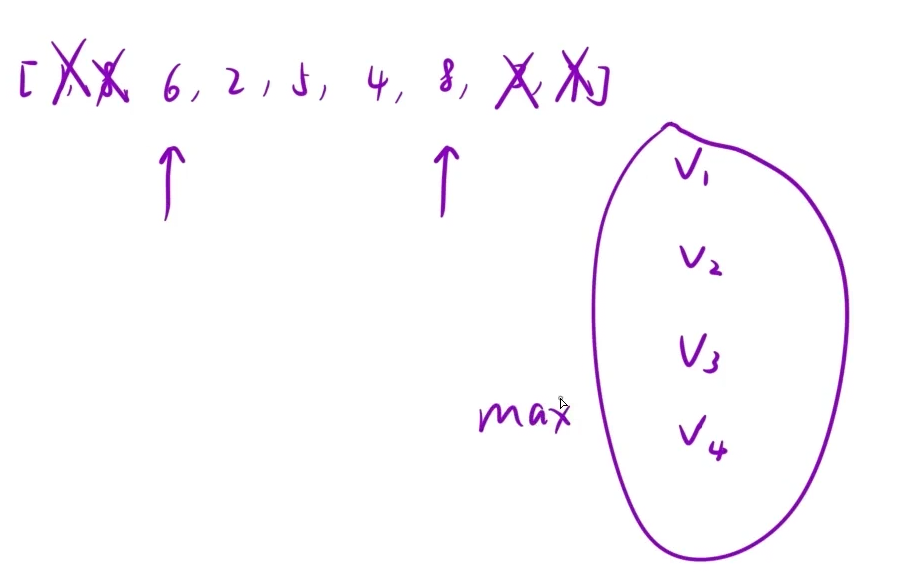
定义两个箭头   就是抽象成了双指针  

利用单调性 使用双指针 遍历数组一遍就找到最终结果(时间复杂度从n的平方直接变成n)

下面是效果图和代码：

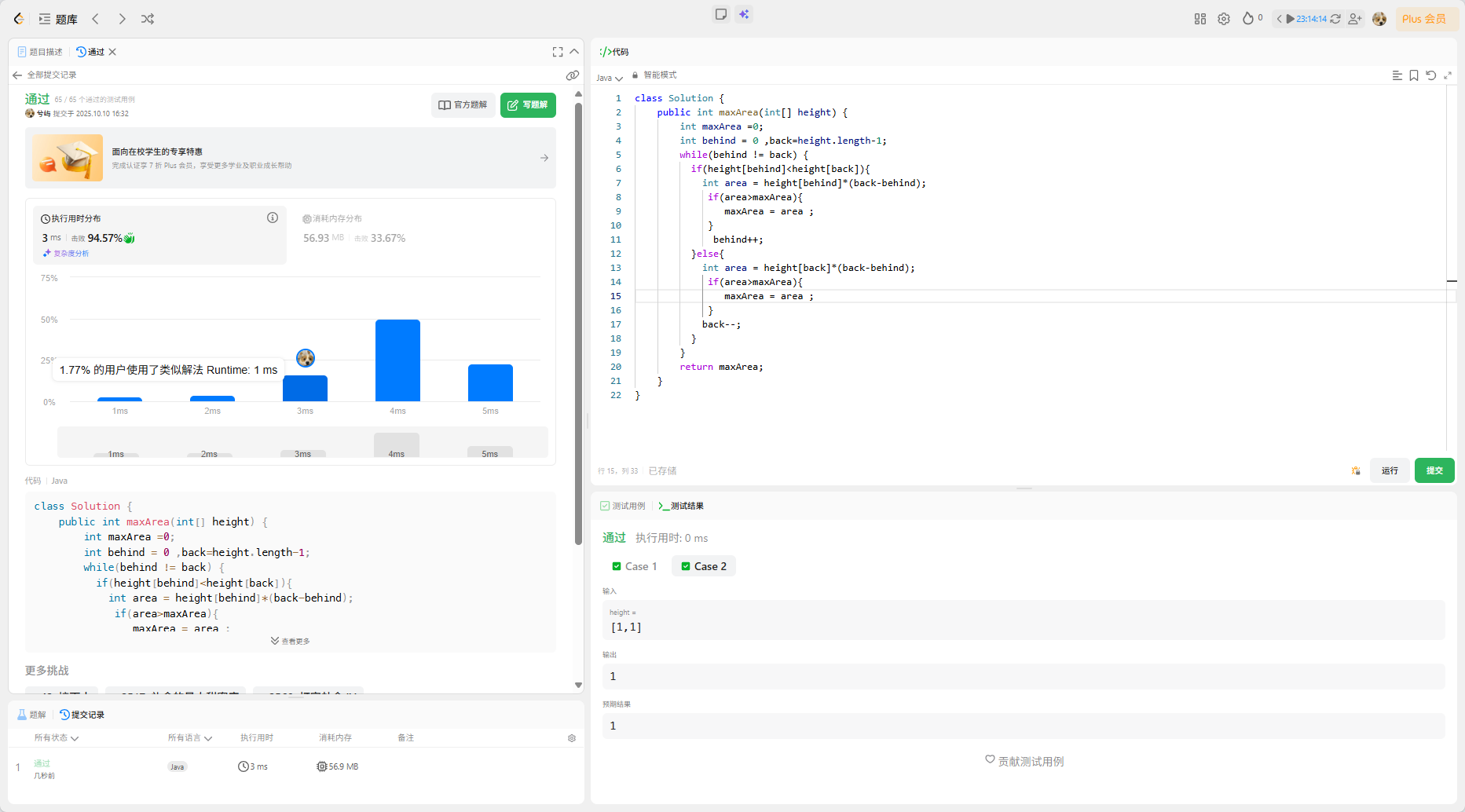
class Solution {public int maxArea(int[] height) {int maxArea =0;int behind = 0 ,back=height.length-1;while(behind != back) {if(height[behind]<height[back]){int area = height[behind]*(back-behind);if(area>maxArea){maxArea = area ;}behind++;}else{int area = height[back]*(back-behind);if(area>maxArea){maxArea = area ;}back--;}}return maxArea;}
}//xiyu251010&1#1*4