线性代数 · 矩阵 | SVD 与 PCA 应用区别
注:本文为 “线性代数 · 矩阵 | SVD 与 PCA” 相关合辑。
英文引文,机翻未校。
中文引文,略作重排。
图片清晰度受引文原图所限。
如有内容异常,请看原文。
1 Singular Value Decomposition and Principal Component Analysis
1 奇异值分解与主成分分析
In these lectures we discuss the SVD and the PCA, two of the most widely used tools in machine learning. Principal Component Analysis (PCA) is a linear dimensionality reduction method dating back to Pearson (1901) and it is one of the most useful techniques in exploratory data analysis. It is also known under different names such as the Karhunen-Love Transform, the Hotelling transform, and Proper Orthogonal Decomposition (POD). PCA can be applied to a data set comprising of nnn vectors x1,...,xn∈Rdx_{1}, ..., x_{n} \in \mathbb{R}^{d}x1,...,xn∈Rd and in turn returns a new basis for Rd\mathbb{R}^{d}Rd whose elements are terms the principal components. It is important that the method is completely data-dependent, that is, the new basis is only a function of the data. The PCA builds on the SVD (or the spectral theorem), we therefore start with the SVD.
在本系列讲座中,我们将探讨机器学习领域中两种应用最广泛的工具——奇异值分解(SVD)和主成分分析(PCA)。主成分分析(PCA)是一种线性降维方法,其起源可追溯至 1901 年(由 Pearson 提出),同时也是探索性数据分析中最实用的技术之一。它还有多个别称,如卡尔曼 - 洛维变换、霍特林变换以及本征正交分解(POD)。对于由 nnn 个向量 x1,...,xn∈Rdx_{1}, ..., x_{n} \in \mathbb{R}^{d}x1,...,xn∈Rd 组成的数据集,可应用 PCA 方法,该方法会返回 Rd\mathbb{R}^{d}Rd 空间的一个新基,这个新基的元素就是主成分。需要重点说明的是,PCA 方法完全依赖数据,也就是说,新基仅仅是数据的函数。由于 PCA 以 SVD(或谱定理)为基础,因此我们首先从 SVD 开始讲解。
1.1 Singular Value Decomposition (SVD)
1.1 奇异值分解(SVD)
Consider a matrix A∈Rm×nA \in \mathbb{R}^{m \times n}A∈Rm×n or Cm×n\mathbb{C}^{m \times n}Cm×n and let us assume that m≥nm \geq nm≥n. Then the singular value decomposition (SVD) of AAA is given by [1] A=UDWA=U D WA=UDW where UUU is m×mm \times mm×m, DDD is m×nm \times nm×n, WWW is n×nn \times nn×n, UUU and WWW are unitary (i.e., U∗U=UU∗=ImU^{*} U=U U^{*}=I_{m}U∗U=UU∗=Im, WW∗=W∗W=InW W^{*}=W^{*} W=I_{n}WW∗=W∗W=In), and DDD is a diagonal (rectangular) matrix
考虑矩阵 A∈Rm×nA \in \mathbb{R}^{m \times n}A∈Rm×n 或 A∈Cm×nA \in \mathbb{C}^{m \times n}A∈Cm×n,且假设 m≥nm \geq nm≥n。那么矩阵 AAA 的奇异值分解(SVD)可表示为[1] A=UDWA=U D WA=UDW,其中 UUU 是 m×mm \times mm×m 矩阵,DDD 是 m×nm \times nm×n 矩阵,WWW 是 n×nn \times nn×n 矩阵;UUU 和 WWW 均为酉矩阵(即满足 U∗U=UU∗=ImU^{*} U=U U^{*}=I_{m}U∗U=UU∗=Im、WW∗=W∗W=InW W^{*}=W^{*} W=I_{n}WW∗=W∗W=In);DDD 是对角(长方)矩阵,其形式为
D=[σ10…00σ2…0⋮⋮⋱⋮000σn0000⋮⋮⋮⋮0000]D=\begin{bmatrix} \sigma_{1} & 0 & \dots & 0 \\ 0 & \sigma_{2} & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \sigma_{n} \\ 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 \end{bmatrix}D=σ10⋮00⋮00σ2⋮00⋮0……⋱00⋮000⋮σn0⋮0
with Dii=σi>0D_{ii}=\sigma_{i}>0Dii=σi>0. Here, σi\sigma_{i}σi are called the singular values of AAA, the columns of UUU are the corresponding left singular vectors, and the columns of WWW are the corresponding right singular vectors.
且满足 Dii=σi>0D_{ii}=\sigma_{i}>0Dii=σi>0。在此,σi\sigma_{i}σi 被称为矩阵 AAA 的奇异值,UUU 的列向量是对应的左奇异向量,WWW 的列向量是对应的右奇异向量。
Let U=[u1,...,um]U=[u_{1}, ..., u_{m}]U=[u1,...,um], W=[w1,...,wn]W=[w_{1}, ..., w_{n}]W=[w1,...,wn] and let rrr be the rank of AAA. Then we can write A=∑i=1rσiuiwi∗A=\sum_{i=1}^{r} \sigma_{i} u_{i} w_{i}^{*}A=∑i=1rσiuiwi∗ with r≤nr \leq nr≤n (and σ1≥σ2≥⋯≥σr\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{r}σ1≥σ2≥⋯≥σr). (So AAA is a sum of weighted rank-one matrices.) The SVD exists for any finite-dimensional matrix.
设 U=[u1,...,um]U=[u_{1}, ..., u_{m}]U=[u1,...,um]、W=[w1,...,wn]W=[w_{1}, ..., w_{n}]W=[w1,...,wn],且 rrr 为矩阵 AAA 的秩,则可将 AAA 表示为 A=∑i=1rσiuiwi∗A=\sum_{i=1}^{r} \sigma_{i} u_{i} w_{i}^{*}A=∑i=1rσiuiwi∗,其中 r≤nr \leq nr≤n(且满足 σ1≥σ2≥⋯≥σr\sigma_{1} \geq \sigma_{2} \geq \cdots \geq \sigma_{r}σ1≥σ2≥⋯≥σr)。(也就是说,AAA 是加权一阶矩阵的和。)任意有限维矩阵都存在奇异值分解。
Remarks
注
-
The uiu_{i}ui are eigenvectors of AA∗A A^{*}AA∗ and the wiw_{i}wi are eigenvectors of A∗AA^{*} AA∗A.
uiu_{i}ui 是 AA∗A A^{*}AA∗ 的特征向量,wiw_{i}wi 是 A∗AA^{*} AA∗A 的特征向量。 -
AA∗A A^{*}AA∗ and A∗AA^{*} AA∗A are positive semidefinite so their eigenvalues are nonnegative.
AA∗A A^{*}AA∗ 和 A∗AA^{*} AA∗A 均为半正定矩阵,因此它们的特征值均非负。 -
If λi\lambda_{i}λi are the eigenvalues of A∗AA^{*} AA∗A, then σi2=λi\sigma_{i}^{2}=\lambda_{i}σi2=λi if λi>0\lambda_{i}>0λi>0. (Here we’re saying that singular values must be positive, but this is more of a matter of taste.)
若 λi\lambda_{i}λi 是 A∗AA^{*} AA∗A 的特征值,且 λi>0\lambda_{i}>0λi>0,则 σi2=λi\sigma_{i}^{2}=\lambda_{i}σi2=λi。(此处我们认为奇异值必须为正,但这更多是一种习惯约定。) -
If AAA is square and Hermitian, then the SVD and the eigenvalue decomposition are the same.
若 AAA 是方阵且为埃尔米特矩阵,则其奇异值分解与特征值分解相同。 -
We could alternatively define the SVD with UUU as an m×nm \times nm×n matrix, DDD as an n×nn \times nn×n matrix, and WWW as an n×nn \times nn×n matrix. In this case, U∗U=InU^{*} U=I_{n}U∗U=In, and W∗W=WW∗=InW^{*} W=W W^{*}=I_{n}W∗W=WW∗=In.
我们也可采用另一种方式定义奇异值分解:令 UUU 为 m×nm \times nm×n 矩阵、DDD 为 n×nn \times nn×n 矩阵、WWW 为 n×nn \times nn×n 矩阵,此时满足 U∗U=InU^{*} U=I_{n}U∗U=In 以及 W∗W=WW∗=InW^{*} W=W W^{*}=I_{n}W∗W=WW∗=In。
Some intuition for SVD: SVD rotates the matrix AAA by UUU and W∗W^{*}W∗ so that AAA becomes a diagonal matrix.
奇异值分解的直观理解:通过 UUU 和 W∗W^{*}W∗ 对矩阵 AAA 进行旋转操作,可使 AAA 转化为对角矩阵。
2 Principal Component Analysis (PCA)
2 主成分分析(PCA)
2.1 Motivation
2.1 研究背景
Given x1,...,xn∈Rdx_{1}, ..., x_{n} \in \mathbb{R}^{d}x1,...,xn∈Rd, we want to project the xix_{i}xi onto Rk\mathbb{R}^{k}Rk, k<dk<dk<d. So, how do we choose kkk and the orientation of the subspace? We consider two ideas:
已知 x1,...,xn∈Rdx_{1}, ..., x_{n} \in \mathbb{R}^{d}x1,...,xn∈Rd,我们希望将 xix_{i}xi 投影到 Rk\mathbb{R}^{k}Rk 空间(其中 k<dk<dk<d)。那么,如何选择 kkk 的值以及子空间的方向呢?我们考虑以下两种思路:
- Find the kkk-dimensional subspace for which the projections of x1,...,xnx_{1}, ..., x_{n}x1,...,xn best approximate the original points x1,...,xnx_{1}, ..., x_{n}x1,...,xn. (We define “best approximation” in the sense of the 2-norm.)
找到一个 kkk 维子空间,使得 x1,...,xnx_{1}, ..., x_{n}x1,...,xn 在该子空间上的投影能最佳逼近原始点 x1,...,xnx_{1}, ..., x_{n}x1,...,xn。(此处“最佳逼近”按 2 - 范数的意义定义。) - We also want to conserve what makes the data points different from each other. Hence, find the kkk-dimensional projection of x1,...,xnx_{1}, ..., x_{n}x1,...,xn that preserves most of the variance of the xix_{i}xi.
我们还希望保留数据点之间的差异特征,因此需要找到 x1,...,xnx_{1}, ..., x_{n}x1,...,xn 的 kkk 维投影,该投影能保留 xix_{i}xi 的大部分方差。
Both of the two ideas above are solved by principal component analysis (PCA).
上述两种思路均可通过主成分分析(PCA)来实现。
2.2 Optimization Problem Formulation [following lecture notes of Singer and Bandeira]
2.2 优化问题构建[参考 Singer 和 Bandeira 的讲义]
We denote the sample mean by
我们将样本均值记为
μn:=1n∑i=1nxi\mu_{n}:=\frac{1}{n} \sum_{i=1}^{n} x_{i}μn:=n1∑i=1nxi
and sample covariance matrix by
样本协方差矩阵记为
∑n:=1n∑i=1n(xi−μn)(xi−μn)∗\sum_{n}:=\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\mu_{n}\right)\left(x_{i}-\mu_{n}\right)^{*}∑n:=n1∑i=1n(xi−μn)(xi−μn)∗.
Let us focus on the first idea in Section 2.1. We want to approximate each xix_{i}xi by an affine low-dimensional subspace such that for each xix_{i}xi we have xi≈μ+∑j=1k(αi)jvjx_{i} \approx \mu+\sum_{j=1}^{k}\left(\alpha_{i}\right)_{j} v_{j}xi≈μ+∑j=1k(αi)jvj, where V:=[v1,...,vk]V:=[v_{1}, ..., v_{k}]V:=[v1,...,vk] is an orthonormal basis to be determined. We can rewrite the above as xi≈μ+Vαix_{i} \approx \mu+V \alpha_{i}xi≈μ+Vαi, where
我们重点关注 2.1 节中的第一种思路。我们希望用一个仿射低维子空间逼近每个 xix_{i}xi,使得对于每个 xix_{i}xi,都有 xi≈μ+∑j=1k(αi)jvjx_{i} \approx \mu+\sum_{j=1}^{k}\left(\alpha_{i}\right)_{j} v_{j}xi≈μ+∑j=1k(αi)jvj,其中 V:=[v1,...,vk]V:=[v_{1}, ..., v_{k}]V:=[v1,...,vk] 是待确定的标准正交基。我们可将上式改写为 xi≈μ+Vαix_{i} \approx \mu+V \alpha_{i}xi≈μ+Vαi,其中
αi=[αi1αi2⋮αik]\alpha_{i}=\begin{bmatrix} \alpha_{i1} \\ \alpha_{i2} \\ \vdots \\ \alpha_{ik} \end{bmatrix}αi=αi1αi2⋮αik
with VVV as a n×kn \times kn×k matrix satisfying V∗V=IkV^{*} V=I_{k}V∗V=Ik. Now, we try to solve the optimization problem
且 VVV 是满足 V∗V=IkV^{*} V=I_{k}V∗V=Ik 的 n×kn \times kn×k 矩阵。目前,我们尝试求解如下优化问题:
minV,α1,...,αnV∗V=IkI:=∑i=1n∥xi−(μ+Vαi)∥22\min _{\substack{V, \alpha_{1}, ..., \alpha_{n} \\ V^{*} V=I_{k}}} I:=\sum_{i=1}^{n}\left\| x_{i}-\left(\mu+V \alpha_{i}\right)\right\| _{2}^{2}V,α1,...,αnV∗V=IkminI:=i=1∑n∥xi−(μ+Vαi)∥22
Thus, we try to minimize the ℓ2\ell_{2}ℓ2-error across all vectors xix_{i}xi. (Unlike in the JL approach we do not strive for minimizing the error uniformly (within an ε\varepsilonε-range) across all xix_{i}xi, but rather the average error.)
也就是说,我们试图最小化所有向量 xix_{i}xi 的 ℓ2\ell_{2}ℓ2 误差。(与约翰逊 - 林登施特劳斯(JL)方法不同,我们并非力求使所有 xix_{i}xi 的误差在 ε\varepsilonε 范围内均匀最小化,而是追求平均误差最小化。)
2.3 Solving the Optimization Problem
2.3 优化问题求解
Fortunately we can separate this problem and first optimize over μ\muμ, then α\alphaα, then over VVV (There are optimization problems which look similar but where you can’t do this strategy of separation of variables.)
幸运的是,我们可以将该问题分解,先对 μ\muμ 进行优化,再对 α\alphaα 进行优化,最后对 VVV 进行优化(有些优化问题看似与此相似,但无法采用这种变量分离策略)。
Let us first optimize with respect to μ\muμ. Without loss of generality, we can assume that ∑i=1nαi=0\sum_{i=1}^{n} \alpha_{i}=0∑i=1nαi=0, because otherwise we could absorb the nonzero ∑iαi\sum_{i} \alpha_{i}∑iαi into μ\muμ. Then, ∂I∂μ=−2∑i=1n(xi−μ−Vαi)\frac{\partial I}{\partial \mu}=-2 \sum_{i=1}^{n}\left(x_{i}-\mu-V \alpha_{i}\right)∂μ∂I=−2∑i=1n(xi−μ−Vαi). Setting the right-hand side equal to zero, we get μ=1n∑i=1nxi=μn\mu = \frac{1}{n} \sum_{i=1}^{n} x_{i} = \mu_{n}μ=n1∑i=1nxi=μn.
首先,我们对 μ\muμ 进行优化。不失一般性,我们可假设 ∑i=1nαi=0\sum_{i=1}^{n} \alpha_{i}=0∑i=1nαi=0,因为若不满足该条件,我们可将非零的 ∑iαi\sum_{i} \alpha_{i}∑iαi 归入 μ\muμ 中。此时,∂I∂μ=−2∑i=1n(xi−μ−Vαi)\frac{\partial I}{\partial \mu}=-2 \sum_{i=1}^{n}\left(x_{i}-\mu-V \alpha_{i}\right)∂μ∂I=−2∑i=1n(xi−μ−Vαi)。令等式右边等于零,可得 μ=1n∑i=1nxi=μn\mu = \frac{1}{n} \sum_{i=1}^{n} x_{i} = \mu_{n}μ=n1∑i=1nxi=μn。
Now let’s optimize in α\alphaα. We calculate: ∂I∂αi=(xi−μ−Vαi)∗V\frac{\partial I}{\partial \alpha_{i}}=\left(x_{i}-\mu-V \alpha_{i}\right)^{*} V∂αi∂I=(xi−μ−Vαi)∗V. Setting the right-hand side equal to zero, we get αi=V∗(xi−μ)\alpha_{i}=V^{*}\left(x_{i}-\mu\right)αi=V∗(xi−μ).
接下来,我们对 α\alphaα 进行优化。经计算可得:∂I∂αi=(xi−μ−Vαi)∗V\frac{\partial I}{\partial \alpha_{i}}=\left(x_{i}-\mu-V \alpha_{i}\right)^{*} V∂αi∂I=(xi−μ−Vαi)∗V。令等式右边等于零,可得 αi=V∗(xi−μ)\alpha_{i}=V^{*}\left(x_{i}-\mu\right)αi=V∗(xi−μ)。
Plugging in the expressions for μ\muμ and αi\alpha_{i}αi into III, we get I=∑i=1n∥xi−μn−VV∗(xi−μn)∥22I=\sum_{i=1}^{n}\left\| x_{i}-\mu_{n}-V V^{*}\left(x_{i}-\mu_{n}\right)\right\| _{2}^{2}I=∑i=1n∥xi−μn−VV∗(xi−μn)∥22 where VV∗V V^{*}VV∗ is an orthogonal projection matrix. Thus, letting yi:=xi−μny_{i}:=x_{i}-\mu_{n}yi:=xi−μn, I=∑i=1n∥yi−VV∗yi∥22I=\sum_{i=1}^{n}\left\| y_{i}-V V^{*} y_{i}\right\| _{2}^{2}I=∑i=1n∥yi−VV∗yi∥22.
将 μ\muμ 和 αi\alpha_{i}αi 的表达式代入 III 中,可得 I=∑i=1n∥xi−μn−VV∗(xi−μn)∥22I=\sum_{i=1}^{n}\left\| x_{i}-\mu_{n}-V V^{*}\left(x_{i}-\mu_{n}\right)\right\| _{2}^{2}I=∑i=1n∥xi−μn−VV∗(xi−μn)∥22,其中 VV∗V V^{*}VV∗ 是正交投影矩阵。因此,令 yi:=xi−μny_{i}:=x_{i}-\mu_{n}yi:=xi−μn,则 I=∑i=1n∥yi−VV∗yi∥22I=\sum_{i=1}^{n}\left\| y_{i}-V V^{*} y_{i}\right\| _{2}^{2}I=∑i=1n∥yi−VV∗yi∥22。
Denote Y=[y1,...,yn]Y=[y_{1}, ..., y_{n}]Y=[y1,...,yn]. Then
令 Y=[y1,...,yn]Y=[y_{1}, ..., y_{n}]Y=[y1,...,yn],则有
minV:V∗V=Ik∑i=1n∥yi−VV∗yi∥22=minV:V∗V=Iktrace[(Y−VV∗Y)∗(Y−VV∗Y)]=minV:V∗V=Iktrace[Y∗(I−VV∗)(I−VV∗)Y]\begin{aligned} \min _{V: V^{*} V=I_{k}} \sum_{i=1}^{n}\left\| y_{i}-V V^{*} y_{i}\right\| _{2}^{2} &= \min _{V: V^{*} V=I_{k}} trace\left[\left(Y-V V^{*} Y\right)^{*}\left(Y-V V^{*} Y\right)\right] \\ &= \min _{V: V^{*} V=I_{k}} trace\left[Y^{*}\left(I-V V^{*}\right)\left(I-V V^{*}\right) Y\right] \end{aligned} V:V∗V=Ikmini=1∑n∥yi−VV∗yi∥22=V:V∗V=Ikmintrace[(Y−VV∗Y)∗(Y−VV∗Y)]=V:V∗V=Ikmintrace[Y∗(I−VV∗)(I−VV∗)Y]
Using properties of the trace (i.e., the circular shift property and linearity), and the fact that (I−VV∗)(I−VV∗)=I−VV∗(I - V V^{*})(I - V V^{*}) = I - V V^{*}(I−VV∗)(I−VV∗)=I−VV∗, we have:
利用迹的性质(即循环移位性质与线性性质),以及 (I−VV∗)(I−VV∗)=I−VV∗(I - V V^{*})(I - V V^{*}) = I - V V^{*}(I−VV∗)(I−VV∗)=I−VV∗ 这一事实,可得:
minV:V∗V=Ik∑i=1n∥yi−VV∗yi∥22=minV:V∗V=Iktrace[YY∗(I−VV∗)]=minV:V∗V=Ik[trace(YY∗)−trace(YY∗VV∗)]=minV:V∗V=Ik[trace(YY∗)−trace(V∗YY∗V)]\begin{aligned} \min _{V:{V^*}V = {I_k}}\sum\limits_{i = 1}^n {\left\| {{y_i} - V{V^*}{y_i}} \right\|_2^2} & = \min _{V:{V^*}V = {I_k}}\operatorname{trace}\left[ {Y{Y^*}\left( {I - V{V^*}} \right)} \right] \\ & = \min _{V:{V^*}V = {I_k}}\left[ \operatorname{trace}\left( {Y{Y^*}} \right) - \operatorname{trace}\left( {Y{Y^*}V{V^*}} \right) \right] \\ & = \min _{V:{V^*}V = {I_k}}\left[ \operatorname{trace}\left( {Y{Y^*}} \right) - \operatorname{trace}\left( {{V^*}Y{Y^*}V} \right) \right] \end{aligned} V:V∗V=Ikmini=1∑n∥yi−VV∗yi∥22=V:V∗V=Ikmintrace[YY∗(I−VV∗)]=V:V∗V=Ikmin[trace(YY∗)−trace(YY∗VV∗)]=V:V∗V=Ikmin[trace(YY∗)−trace(V∗YY∗V)]
But YYY does not depend on VVV! Hence, the minimum in the above formula is independent of the term trace(YY∗)trace(Y Y^{*})trace(YY∗), and thus is equivalent to the solution of the following optimization problem:
但 YYY 与 VVV 无关!因此,上式中的最小值与 trace(YY∗)trace(Y Y^{*})trace(YY∗) 无关,从而等同于如下优化问题的解:
maxV:V∗V=Ik1ntrace(V∗YY∗V)=maxV:V∗V=Iktrace(V∗∑nV)\max _{V: V^{*} V=I_{k}} \frac{1}{n} trace\left(V^{*} Y Y^{*} V\right)=\max _{V: V^{*} V=I_{k}} trace\left(V^{*} \sum_{n} V\right)V:V∗V=Ikmaxn1trace(V∗YY∗V)=V:V∗V=Ikmaxtrace(V∗n∑V)
Let ∑n\sum _{n}∑n have the eigenvalue decomposition ∑n=∑i=1dλivivi∗\sum_{n}=\sum_{i=1}^{d} \lambda_{i} v_{i} v_{i}^{*}∑n=∑i=1dλivivi∗ (note: the original text uses nnn as the upper limit, which is corrected here to ddd to match the dimension of the data space Rd\mathbb{R}^dRd) where λi≥0\lambda_{i} \geq0λi≥0. ( λi\lambda_{i}λi cannot be negative because ∑n\sum _{n}∑n is positive semidefinite.) Here, λi\lambda_{i}λi are the eigenvalues of ∑n\sum _{n}∑n, and viv_{i}vi are the corresponding eigenvectors. Since ∑n\sum _{n}∑n is a symmetric matrix, its eigenvectors viv_{i}vi are mutually orthogonal.
设 ∑n\sum _{n}∑n 的特征值分解为 ∑n=∑i=1dλivivi∗\sum_{n}=\sum_{i=1}^{d} \lambda_{i} v_{i} v_{i}^{*}∑n=∑i=1dλivivi∗(注:原文以上限 nnn 表述,此处修正为数据空间 Rd\mathbb{R}^dRd 的维度 ddd,以保证逻辑一致性),其中 λi≥0\lambda_{i} \geq0λi≥0(由于 ∑n\sum _{n}∑n 是半正定矩阵,因此 λi\lambda_{i}λi 不可能为负)。此处,λi\lambda_{i}λi 是 ∑n\sum _{n}∑n 的特征值,viv_{i}vi 是对应的特征向量。由于 ∑n\sum _{n}∑n 是对称矩阵,其特征向量 viv_{i}vi 相互正交。
From linear algebra, we know that:
由线性代数知识可知:
maxV:V∗V=Iktrace(V∗∑nV)=∑i=1kλi\max _{V: V^{*} V=I_{k}} trace\left(V^{*} \sum_{n} V\right)=\sum_{i=1}^{k} \lambda_{i}V:V∗V=Ikmaxtrace(V∗n∑V)=i=1∑kλi
Moreover, the VVV that achieves this maximum is given by V=[v1,...,vk]V=[v_{1}, ..., v_{k}]V=[v1,...,vk], where v1,...,vkv_{1}, ..., v_{k}v1,...,vk are the eigenvectors corresponding to the kkk largest eigenvalues of ∑n\sum _{n}∑n. Hence, these specific vjv_{j}vj provide the desired optimal orthonormal basis for our data xix_{i}xi.
且实现该最大值的 VVV 为 V=[v1,...,vk]V=[v_{1}, ..., v_{k}]V=[v1,...,vk],其中 v1,...,vkv_{1}, ..., v_{k}v1,...,vk 是 ∑n\sum _{n}∑n 的 kkk 个最大特征值对应的特征向量。因此,这些特定的 vjv_{j}vj 为数据 xix_{i}xi 提供了所需的最优标准正交基。
2.4 Intuition for PCA
2.4 主成分分析的直观理解
PCA first performs the eigenvalue decomposition of ∑n\sum _{n}∑n, then treats the projections of centered data points (where “centered” means subtracting the sample mean μn\mu_{n}μn) onto the kkk top eigenvectors of the sample covariance matrix ∑n\sum _{n}∑n as the principal components. (The “k top eigenvectors” refer to the eigenvectors associated with the kkk largest eigenvalues.)
主成分分析首先对 ∑n\sum _{n}∑n 进行特征值分解,然后将中心化数据点(“中心化”即减去样本均值 μn\mu_{n}μn)在样本协方差矩阵 ∑n\sum _{n}∑n 的 kkk 个“顶级特征向量”上的投影定义为主成分(“kkk 个顶级特征向量”指与 kkk 个最大特征值相关联的特征向量)。
2.5 Cost for PCA
2.5 主成分分析的计算成本
The computational cost of the PCA procedure without using SVD is as follows:
不使用 SVD 的 PCA 流程,其计算成本如下:
-
Constructing the sample covariance matrix ∑n\sum _{n}∑n requires O(nd2)O(n d^{2})O(nd2) operations (where nnn is the number of data points and ddd is the dimension of each data point).
构建样本协方差矩阵 ∑n\sum _{n}∑n 需要 O(nd2)O(n d^{2})O(nd2) 次运算(其中 nnn 为数据点数量,ddd 为单个数据点的维度)。 -
If we use a traditional, naive method to perform eigenvalue decomposition for solving VVV, it requires O(d3)O(d^{3})O(d3) operations.
若采用传统、朴素的方法进行特征值分解以求解 VVV,则需要 O(d3)O(d^{3})O(d3) 次运算。
However, the cost can be slightly reduced by using SVD, as explained below.
不过,通过 SVD 方法可略微降低计算成本,具体说明如下。
Let X=[x1,...,xn]X=[x_{1}, ..., x_{n}]X=[x1,...,xn] (an d×nd \times nd×n matrix, where each column is a data point) and
令 X=[x1,...,xn]X=[x_{1}, ..., x_{n}]X=[x1,...,xn](d×nd \times nd×n 矩阵,每一列代表一个数据点),且
KaTeX parse error: Unknown column alignment: * at position 40: …{\begin{array}{*̲{20}{c}} 1\\1\\… (an n×1n \times 1n×1 vector with nnn ones). (n×1n \times 1n×1 向量,包含 nnn 个 1)
Then the sample covariance matrix can be rewritten as:
则样本协方差矩阵可改写为:
∑n=1n(X−μn1n∗)(X−μn1n∗)∗\sum _{n}=\frac{1}{n}(X-\mu_{n} 1_{n}^{*})(X-\mu_{n} 1_{n}^{*})^{*}n∑=n1(X−μn1n∗)(X−μn1n∗)∗
The key idea to reduce computational cost is to directly compute the SVD of the centered data matrix A:=X−μn1n∗A:=X-\mu_{n} 1_{n}^{*}A:=X−μn1n∗, instead of first constructing ∑n\sum _{n}∑n.
降低计算成本的核心思路是:直接计算中心化数据矩阵 A:=X−μn1n∗A:=X-\mu_{n} 1_{n}^{*}A:=X−μn1n∗ 的 SVD,而非先构建 ∑n\sum _{n}∑n。
The left singular vectors of AAA are exactly the eigenvectors of AA∗=n∑nA A^{*}=n\sum _{n}AA∗=n∑n, i.e., they are the same as the eigenvectors v1,...,vdv_{1}, ..., v_{d}v1,...,vd of ∑n\sum _{n}∑n. Therefore, the computational cost of PCA via SVD is O(min{n2d,nd2})O(\min \{n^{2} d, n d^{2}\})O(min{n2d,nd2}), which is more efficient than the traditional method when nnn and ddd are large.
矩阵 AAA 的左奇异向量恰好是 AA∗=n∑nA A^{*}=n\sum _{n}AA∗=n∑n 的特征向量,即与 ∑n\sum _{n}∑n 的特征向量 v1,...,vdv_{1}, ..., v_{d}v1,...,vd 完全一致。因此,通过 SVD 实现 PCA 的计算成本为 O(min{n2d,nd2})O(\min \{n^{2} d, n d^{2}\})O(min{n2d,nd2}),在 nnn 和 ddd 较大时,该成本低于传统方法。
Furthermore, from the full SVD of AAA, we can obtain all left singular vectors v1,...,vdv_{1}, ..., v_{d}v1,...,vd. However, in practice, we only need the first kkk left singular vectors v1,...,vkv_{1}, ..., v_{k}v1,...,vk (where k<dk<dk<d, and often k≪dk \ll dk≪d for dimensionality reduction). Computing only the top kkk singular vectors can be done in O(dnk)O(d n k)O(dnk) operations—this is much faster than computing the full SVD. In MATLAB, this can be implemented with the svds command, which internally uses Lanczos-type iterative methods to efficiently find the top kkk singular vectors.
此外,通过 AAA 的完整 SVD,我们可得到全部左奇异向量 v1,...,vdv_{1}, ..., v_{d}v1,...,vd。但在实际降维场景中,我们通常仅需前 kkk 个左奇异向量 v1,...,vkv_{1}, ..., v_{k}v1,...,vk(其中 k<dk<dk<d,且常满足 k≪dk \ll dk≪d)。仅计算前 kkk 个奇异向量仅需 O(dnk)O(d n k)O(dnk) 次运算,远快于完整 SVD 的计算。在 MATLAB 中,可通过 svds 命令实现该操作,该命令内部采用兰索斯(Lanczos)型迭代方法,能高效求解前 kkk 个奇异向量。
We also note that randomized SVD algorithms can further reduce this cost to O(ndlog(k)+(n+d)k2)O(n d \log (k)+(n+d) k^{2})O(ndlog(k)+(n+d)k2). This type of algorithm uses random sampling to reduce the dimension of the original matrix first, then performs SVD on the low-dimensional matrix—this is particularly effective for large-scale data sets, and we will discuss it in more detail later.
我们还需注意,随机化 SVD 算法可将计算成本进一步降低至 O(ndlog(k)+(n+d)k2)O(n d \log (k)+(n+d) k^{2})O(ndlog(k)+(n+d)k2)。这类算法通过随机采样先对原始矩阵进行降维,再对低维矩阵进行 SVD,在大规模数据集上效果尤为显著,后续我们将对其展开更详细的讨论。
2.6 Another Optimality Property of the SVD
2.6 奇异值分解的另一最优性性质
Let A∈Rm×nA \in \mathbb{R}^{m \times n}A∈Rm×n with m≥nm \geq nm≥n, and let its full SVD be A=∑i=1nσiuiwi∗A=\sum_{i=1}^{n} \sigma_{i} u_{i} w_{i}^{*}A=∑i=1nσiuiwi∗ (where σ1≥σ2≥⋯≥σn>0\sigma_{1} \geq \sigma_{2} \geq \dots \geq \sigma_{n}>0σ1≥σ2≥⋯≥σn>0 are the singular values, ui∈Rmu_{i} \in \mathbb{R}^mui∈Rm are the left singular vectors, and wi∈Rnw_{i} \in \mathbb{R}^nwi∈Rn are the right singular vectors). For k<nk<nk<n, define the rank-kkk truncated SVD of AAA as:
设 A∈Rm×nA \in \mathbb{R}^{m \times n}A∈Rm×n 且 m≥nm \geq nm≥n,其完整 SVD 为 A=∑i=1nσiuiwi∗A=\sum_{i=1}^{n} \sigma_{i} u_{i} w_{i}^{*}A=∑i=1nσiuiwi∗(其中 σ1≥σ2≥⋯≥σn>0\sigma_{1} \geq \sigma_{2} \geq \dots \geq \sigma_{n}>0σ1≥σ2≥⋯≥σn>0 为奇异值,ui∈Rmu_{i} \in \mathbb{R}^mui∈Rm 为左奇异向量,wi∈Rnw_{i} \in \mathbb{R}^nwi∈Rn 为右奇异向量)。对于 k<nk<nk<n,定义 AAA 的秩-kkk 截断 SVD为:
Ak=∑i=1kσiuiwi∗A_{k}=\sum_{i=1}^{k} \sigma_{i} u_{i} w_{i}^{*}Ak=i=1∑kσiuiwi∗
Given matrix AAA, for any matrix BBB with rank at most kkk, the following best approximation result holds:
已知矩阵 AAA,对于任意秩不超过 kkk 的矩阵 BBB,有如下最佳逼近结果:
∥A−Ak∥op≤∥A−B∥op\left\| A-A_{k}\right\| _{op } \leq\| A-B\| _{op }∥A−Ak∥op≤∥A−B∥op
and 且
∥A−Ak∥op=σk+1\left\|A-A_{k}\right\|_{op }=\sigma_{k+1}∥A−Ak∥op=σk+1
In other words, the rank-kkk truncated SVD AkA_{k}Ak is the best rank-kkk approximation to AAA under the operator norm (also known as the spectral norm). This property is crucial for linking SVD to PCA: the PCA projection of data is essentially equivalent to using the truncated SVD of the centered data matrix to approximate the original data.
也就是说,在算子范数(又称谱范数)下,秩-kkk 截断 SVD AkA_{k}Ak 是 AAA 的最佳秩-kkk 逼近矩阵。该性质是 SVD 与 PCA 关联的核心:数据的 PCA 投影本质上等价于用中心化数据矩阵的截断 SVD 逼近原始数据。
References
参考文献
[1] G.H. Golub and C.F. van Loan. Matrix Computations. Johns Hopkins University Press, Baltimore, third edition, 1996.
[1] G.H. 古尔布(G.H. Golub)、C.F. 范洛恩(C.F. van Loan). 《矩阵计算》. 约翰斯·霍普金斯大学出版社,巴尔的摩,第三版,1996 年.
Additional Notes
-
Note: Inside the
svdscommand in MATLAB, the eigenvector decomposition is actually implemented via theeigscommand in a more efficient way. This is because the top singular vectors of AAA correspond to the top eigenvectors of AA∗A A^{*}AA∗ (or A∗AA^{*} AA∗A), sosvdsleverages the optimization ofeigsfor finding top eigenvectors.
注:在 MATLAB 的svds命令内部,特征值分解实际上是通过eigs命令以更高效的方式实现的。这是因为 AAA 的前 kkk 个奇异向量对应于 AA∗A A^{*}AA∗(或 A∗AA^{*} AA∗A)的前 kkk 个特征向量,因此svds借助了eigs在求解顶级特征向量上的优化设计。 -
This efficiency is related to the use of power iteration methods (a type of iterative algorithm) to compute the top eigenvector very quickly. A classic application of this is Google’s PageRank algorithm: when ranking websites based on keyword searches, PageRank needs to compute the top eigenvector of an extremely large adjacency matrix (representing website links), and power iteration is the core method to achieve this efficiently.
这种高效性与幂迭代法(一种迭代算法)的使用有关,该方法能快速计算出顶级特征向量。谷歌的网页排名(PageRank)算法就是一个典型应用:在根据关键词搜索对网站进行排名时,PageRank 需要计算一个规模极大的邻接矩阵(表示网站间的链接关系)的顶级特征向量,而幂迭代法则是高效实现这一计算的核心方法。
线性代数概念:特征值、奇异值与降维方法(PCA/SVD)
前言
线性代数中,特征值与特征向量、奇异值与奇异向量是描述矩阵本质的工具,而基于二者发展的主成分分析(PCA) 与奇异值分解(SVD) 则是数据降维、信息提取的关键技术。
一、特征值与特征向量(方阵专属工具)
1.1 定义:描述方阵的线性变换本质
仅适用于 nnn 阶方阵(行数=列数),定义如下:
设 AAA 为 nnn 阶方阵,若存在复数 λ\lambdaλ 和 nnn 维非零向量 xxx,满足:
Ax=λxAx = \lambda xAx=λx
则称 λ\lambdaλ 为 AAA 的特征值,非零向量 xxx 为 AAA 对应 λ\lambdaλ 的特征向量。
- 关键约束:特征向量必须非零(若 x=0x=0x=0,则对任意 λ\lambdaλ 均满足等式,无实际意义);
- 取值范围:特征值 λ\lambdaλ 可属于复数域(如非对称实方阵可能有共轭复特征值),可正、可负、可为零。
1.2 双重意义:代数与几何视角
1.2.1 代数意义:简化矩阵运算
将复杂的"矩阵-向量乘法"转化为"数-向量乘法(数乘)",例如对向量序列 x,Ax,A2x,…,Akxx, Ax, A^2x, \dots, A^kxx,Ax,A2x,…,Akx,若 xxx 是 AAA 的特征向量(对应 λ\lambdaλ),则:
Akx=λkxA^kx = \lambda^kxAkx=λkx
避免高次矩阵乘法的繁琐计算,适用于马尔可夫链、动态系统迭代等场景。
1.2.2 几何意义:刻画线性变换效果
在欧几里得空间中,矩阵 AAA 代表线性变换(伸缩、旋转、投影),特征值与特征向量的几何角色为:
- 特征向量:变换的"稳定方向"——向量经 AAA 变换后,仅沿原方向(或反方向,λ<0\lambda<0λ<0 时)伸缩,不改变方向;
- 特征值:“伸缩比例因子”——∣λ∣|\lambda|∣λ∣ 反映幅度(∣λ∣>1|\lambda|>1∣λ∣>1 拉伸,0<∣λ∣<10<|\lambda|<10<∣λ∣<1 压缩,∣λ∣=1|\lambda|=1∣λ∣=1 无伸缩),符号反映方向是否反转。
1.3 特征值分解:构建线性空间的"自然基"
1.3.1 基的要求
“基"是线性空间中线性无关的向量组,需满足:空间内任意向量可由该组向量线性组合表示(类比直角坐标系的 x/yx/yx/y 轴向量)。线性无关的本质是"无冗余”——任意基向量不能由其他基向量组合得到,否则会导致空间维度"坍缩"。
1.3.2 实对称方阵的特征值分解(特殊且常用)
实对称方阵(满足 AT=AA^T=AAT=A)的特征向量两两正交,可构成"标准正交基",其分解形式为:
A=QΛQTA = Q\Lambda Q^TA=QΛQT
各矩阵含义:
- QQQ:n×nn \times nn×n 正交矩阵(QTQ=IQ^TQ=IQTQ=I,III 为单位矩阵),列向量为 AAA 的标准正交特征向量;
- Λ\LambdaΛ:n×nn \times nn×n 对角矩阵,对角元素为 AAA 的特征值(顺序可任意),∣λi∣|\lambda_i|∣λi∣ 越大,对应方向的变换效果越显著(数据视角:方差越大、信息量越多)。
1.4 特征值的存在性与矩阵奇异性
任意方阵(无论奇异/非奇异)在复数域内均存在特征值,其取值与矩阵奇异性(行列式)直接相关:
| 矩阵类型 | 行列式定义 | 特征值性质 |
|---|---|---|
| 奇异矩阵 | det(A)=0\det(A)=0det(A)=0 | 至少含一个特征值为 0(因行列式=所有特征值乘积,det(A)=0⟹∃λi=0\det(A)=0 \implies \exists \lambda_i=0det(A)=0⟹∃λi=0) |
| 非奇异矩阵 | det(A)≠0\det(A)\neq0det(A)=0 | 所有特征值非零(若 ∃λi=0\exists \lambda_i=0∃λi=0,则 det(A)=0\det(A)=0det(A)=0,与非奇异矛盾) |
1.5 应用与局限
1.5.1 应用:PCA 数据降维(基于协方差矩阵)
- 对数据的协方差矩阵(实对称方阵)做特征值分解;
- 最大特征值对应的数据方向方差最大(含主要信息),极小特征值方向信息冗余;
- 选取前 kkk 个最大特征值对应的特征向量(主成分),将高维数据投影到 kkk 维空间,实现降维且保留核心信息。
1.5.2 局限:仅适用于方阵
特征值分解依赖"向量变换前后维度不变",无法处理非方阵(如 m×nm \times nm×n 样本-特征矩阵、图像矩阵),需通过奇异值分解解决。
二、奇异值与奇异值分解(任意矩阵通用)
2.1 定义:突破方阵限制的"广义特征"
为解决非方阵的特征提取问题,引入奇异值与奇异值分解(SVD),适用于任意 m×nm \times nm×n 矩阵(方阵/非方阵、实/复矩阵)。
SVD 的核心是将矩阵分解为三个特殊矩阵的乘积,形式为:
A=UΣVTA = U\Sigma V^TA=UΣVT
各矩阵的维度、性质与含义(实矩阵场景,复矩阵需将 TTT 替换为共轭转置 HHH):
| 矩阵符号 | 维度 | 性质 | 名称与含义 |
|---|---|---|---|
| UUU | m×mm \times mm×m | 正交矩阵(UTU=ImU^TU=I_mUTU=Im) | 左奇异矩阵,列向量为 AAA 的左奇异向量(对应 AATAA^TAAT 的特征向量) |
| VVV | n×nn \times nn×n | 正交矩阵(VTV=InV^TV=I_nVTV=In) | 右奇异矩阵,列向量为 AAA 的右奇异向量(对应 ATAA^TAATA 的特征向量) |
| Σ\SigmaΣ | m×nm \times nm×n | 对角矩阵 | 奇异值矩阵,对角元素为 AAA 的奇异值,按降序排列(σ1≥σ2≥⋯≥σr≥0\sigma_1 \geq \sigma_2 \geq \dots \geq \sigma_r \geq 0σ1≥σ2≥⋯≥σr≥0,rrr 为 AAA 的秩) |
- 关键性质:奇异值均为非负实数,前 rrr 个严格为正(rrr 为矩阵秩),其余为 0。
2.2 几何意义:线性变换的三步拆解(以二维为例)
任意线性变换可通过 SVD 分解为"旋转/反射→伸缩→旋转/反射"三步,直观理解如下:
- 右奇异矩阵 VVV:将原始空间的标准正交基(如 (1,0)T,(0,1)T(1,0)^T, (0,1)^T(1,0)T,(0,1)T)旋转/反射为新正交基 v1,v2v_1, v_2v1,v2(右奇异向量);
- 奇异值矩阵 Σ\SigmaΣ:对 v1,v2v_1, v_2v1,v2 按奇异值 σ1,σ2\sigma_1, \sigma_2σ1,σ2 伸缩,得到 σ1v1,σ2v2\sigma_1v_1, \sigma_2v_2σ1v1,σ2v2;
- 左奇异矩阵 UUU:将伸缩后的基旋转/反射为最终正交基 u1,u2u_1, u_2u1,u2(左奇异向量)。
简言之,奇异值决定"伸缩幅度",左右奇异矩阵决定"方向变换",三者共同包含线性变换的全部信息。
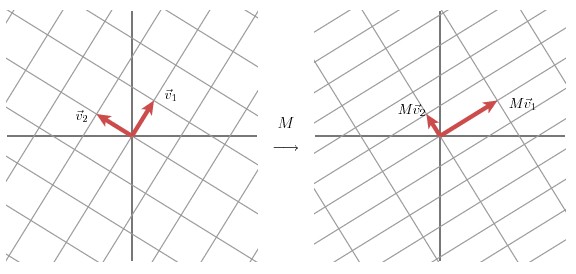
(图 1:原始正交基经 VVV 旋转/反射得到 v1,v2v_1, v_2v1,v2)

(图 2:伸缩后的 σ1v1,σ2v2\sigma_1v_1, \sigma_2v_2σ1v1,σ2v2 经 UUU 旋转/反射得到 u1,u2u_1, u_2u1,u2)
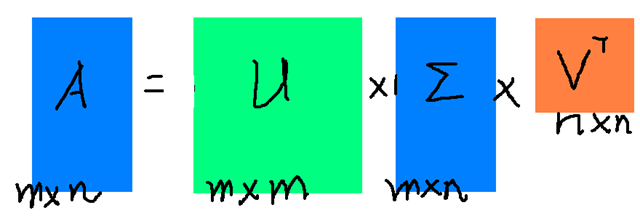
(图 3:A=UΣVTA=U\Sigma V^TA=UΣVT 的矩阵关系,VVV 对应原始基,UUU 对应变换后基,Σ\SigmaΣ 对应伸缩)
2.3 应用:矩阵近似与数据压缩
奇异值的核心特性是"衰减速度极快"——前 rrr 个(r≪m,nr \ll m,nr≪m,n)最大奇异值的和通常占全部奇异值和的 99%99\%99% 以上,因此可通过部分奇异值分解实现高效压缩:
对 m×nm \times nm×n 矩阵 AAA,取前 kkk 个(k≤rk \leq rk≤r)最大奇异值及对应左右奇异向量,构建近似:
A≈UkΣkVkTA \approx U_k\Sigma_kV_k^TA≈UkΣkVkT
其中:
- UkU_kUk:m×km \times km×k 矩阵(取 UUU 前 kkk 列);
- Σk\Sigma_kΣk:k×kk \times kk×k 对角矩阵(取 Σ\SigmaΣ 前 kkk 个奇异值);
- VkTV_k^TVkT:k×nk \times nk×n 矩阵(取 VTV^TVT 前 kkk 行)。
存储优势:原始矩阵需存储 m×nm \times nm×n 个元素,而 Uk,Σk,VkTU_k, \Sigma_k, V_k^TUk,Σk,VkT 共需存储 k(m+n+1)k(m+n+1)k(m+n+1) 个元素(例:m=n=1000,k=50m=n=1000, k=50m=n=1000,k=50 时,存储量从 10610^6106 降至 100050100050100050)。
三、特征值与奇异值的关联
二者通过"矩阵与其转置的乘积"建立数学关联,需按"非方阵"和"方阵"分类讨论,确保逻辑无重复。
3.1 非方阵:奇异值由关联方阵的特征值推导
非方阵无特征值,其奇异值需通过以下步骤计算:
- 对 m×nm \times nm×n 矩阵 AAA,计算两个关联方阵:
- ATAA^TAATA:n×nn \times nn×n 实对称方阵((ATA)T=ATA(A^TA)^T=A^TA(ATA)T=ATA);
- AATAA^TAAT:m×mm \times mm×m 实对称方阵((AAT)T=AAT(AA^T)^T=AA^T(AAT)T=AAT)。
- 核心性质:ATAA^TAATA 与 AATAA^TAAT 的非零特征值完全相同(设为 λ1≥λ2≥⋯≥λr>0\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_r > 0λ1≥λ2≥⋯≥λr>0,rrr 为 AAA 的秩),仅零特征值个数不同(ATAA^TAATA 有 n−rn-rn−r 个,AATAA^TAAT 有 m−rm-rm−r 个)。
- 奇异值定义:AAA 的奇异值 = 非零特征值的算术平方根,即:
σi=λi(i=1,2,…,r)\sigma_i = \sqrt{\lambda_i} \quad (i=1,2,\dots,r)σi=λi(i=1,2,…,r)
同时,奇异向量与关联方阵的特征向量直接对应:
- ATAA^TAATA 的特征向量 = AAA 的右奇异向量(构成 VVV 的列);
- AATAA^TAAT 的特征向量 = AAA 的左奇异向量(构成 UUU 的列);
- 左、右奇异向量满足:ui=1σiAviu_i = \frac{1}{\sigma_i}Av_iui=σi1Avi(σi≠0\sigma_i \neq 0σi=0)。
3.2 方阵:奇异值与特征值的关系
方阵同时存在特征值和奇异值,需分"实对称"和"非对称"两类:
3.2.1 实对称方阵(特殊场景)
若 AAA 为实对称方阵(AT=AA^T=AAT=A),则:
σi=∣λi∣\sigma_i = |\lambda_i|σi=∣λi∣
- 原因:实对称方阵的特征值为实数,且 ATA=A2A^TA=A^2ATA=A2,因此 ATAA^TAATA 的特征值 = AAA 特征值的平方(λATA,i=λA,i2\lambda_{A^TA,i} = \lambda_{A,i}^2λATA,i=λA,i2),代入奇异值公式得 σi=λATA,i=∣λi∣\sigma_i = \sqrt{\lambda_{A^TA,i}} = |\lambda_i|σi=λATA,i=∣λi∣。
- 示例:A=(200−3)A=\begin{pmatrix}2&0\\0&-3\end{pmatrix}A=(200−3),特征值 λ1=2,λ2=−3\lambda_1=2, \lambda_2=-3λ1=2,λ2=−3,奇异值 σ1=2,σ2=3\sigma_1=2, \sigma_2=3σ1=2,σ2=3,即 σi=∣λi∣\sigma_i=|\lambda_i|σi=∣λi∣。
3.2.2 非对称方阵(一般场景)
非对称方阵的奇异值与自身特征值无"绝对值相等"的关系,需通过 3.1 节的通用方法计算(先求 ATAA^TAATA 或 AATAA^TAAT 的特征值,再取平方根)。
- 示例:A=(1234)A=\begin{pmatrix}1&2\\3&4\end{pmatrix}A=(1324)
- 计算 ATA=(10141420)A^TA=\begin{pmatrix}10&14\\14&20\end{pmatrix}ATA=(10141420);
- 求 ATAA^TAATA 的特征值:λ1≈29.87,λ2≈0.13\lambda_1 \approx 29.87, \lambda_2 \approx 0.13λ1≈29.87,λ2≈0.13;
- 奇异值:σ1≈5.46,σ2≈0.36\sigma_1 \approx 5.46, \sigma_2 \approx 0.36σ1≈5.46,σ2≈0.36;
- 对比 AAA 自身特征值:λ1≈5.70,λ2≈−0.70\lambda_1 \approx 5.70, \lambda_2 \approx -0.70λ1≈5.70,λ2≈−0.70,可见二者无直接绝对值关联。
3.3 差异对比(表格化呈现,避免重复)
| 对比维度 | 特征值(Eigenvalue) | 奇异值(Singular Value) |
|---|---|---|
| 适用矩阵类型 | 仅方阵(n×nn \times nn×n) | 任意矩阵(m×nm \times nm×n,m,nm,nm,n 可不等) |
| 计算逻辑 | 直接解原方阵的特征方程 det(A−λI)=0\det(A-\lambda I)=0det(A−λI)=0 | 先求 ATAA^TAATA 或 AATAA^TAAT 的特征值,再取平方根 |
| 取值范围 | 复数域(可正、负、零;实对称方阵为实数) | 非负实数(σi≥0\sigma_i \geq 0σi≥0,按降序排列) |
| 核心作用 | 描述方阵的变换幅度、特征向量贡献度 | 描述任意矩阵的变换幅度、信息量、近似精度 |
| 数据关联 | 实对称方阵(如协方差矩阵)的特征值对应数据方差 | 任意矩阵的奇异值对应数据在奇异向量方向的"能量" |
四、降维方法:PCA 与 SVD 的联系与区别
基于前文的特征值/奇异值理论,进一步梳理两种降维方法的逻辑,确保与前文知识点衔接且无重复。
4.1 方法本质与目标
4.1.1 PCA(主成分分析)
- 本质:数据降维方法,目标是在降维过程中最大限度保留原始数据信息。
- 优化准则:找到 kkk 个单位正交基(主成分),使数据投影到这些基上后:
- 各维度方差最大(数据离散度最高,保留更多信息);
- 各维度协方差为 0(无信息冗余)。
4.1.2 SVD(奇异值分解)
- 本质:矩阵分解方法,目标是将任意矩阵拆分为 UΣVTU\Sigma V^TUΣVT 的标准形式。
- 应用范围:不局限于降维,还可用于矩阵近似、数据压缩、图像去噪、伪逆求解等,降维仅为其应用场景之一。
4.2 计算逻辑与效率差异
4.2.1 内在联系:PCA 可通过 SVD 实现
PCA 的关键步骤是对协方差矩阵做特征值分解,而该过程可通过 SVD 简化:
- 设样本矩阵为 Xm×nX_{m \times n}Xm×n(mmm 样本数,nnn 特征数),PCA 需计算协方差矩阵 C=1mXXTC = \frac{1}{m}XX^TC=m1XXT;
- SVD 中,XTXX^TXXTX 的特征向量 = SVD 的右奇异矩阵 VVV,且 XTXX^TXXTX 的特征值 = XXX 奇异值的平方(λi=σi2\lambda_i = \sigma_i^2λi=σi2);
- PCA 所需的“主成分”(协方差矩阵 CCC 最大 kkk 个特征值对应的特征向量),等价于 SVD 中右奇异矩阵 VVV 的前 kkk 个列向量。因此,无需直接计算协方差矩阵,通过 SVD 即可间接实现 PCA。
4.2.2 效率对比:SVD 更适用于高维/稀疏数据
| 对比维度 | PCA(基于特征值分解) | SVD(奇异值分解) |
|---|---|---|
| 计算复杂度 | 需先构建协方差矩阵(若 n=104n=10^4n=104,则 CCC 为 104×10410^4 \times 10^4104×104 矩阵),存储与计算成本极高 | 支持部分 SVD 算法(如随机 SVD),无需构建协方差矩阵,直接求解核心奇异向量,内存消耗低 |
| 稳定性 | 高维矩阵特征值分解易出现数值不稳定问题 | 迭代计算逻辑更稳健,数值精度更高 |
| 维度压缩灵活性 | 仅能压缩“特征维度”(列维度),无法处理“样本维度”(行维度) | 可通过左奇异矩阵 UUU 压缩样本维度(X′=Uk×mTXX' = U_{k \times m}^T XX′=Uk×mTX),也可通过 VVV 压缩特征维度,灵活性更高 |
4.3 数据适应性:对稀疏矩阵的处理能力
实际场景中,样本矩阵常为稀疏矩阵(如 NLP 词袋模型、高维特征数据,大部分元素为 0),二者适应性差异显著:
4.3.1 PCA 的缺陷
PCA 需先对样本进行中心化处理(每个特征减去其均值),该操作会将稀疏矩阵中的 0 元素转化为非 0 元素(例:某特征均值为 0.5,原 0 元素变为 -0.5),直接破坏矩阵稀疏性。稀疏性丢失后,矩阵需从“稀疏存储格式”转为“稠密存储格式”,存储空间与计算成本呈指数级增长。
4.3.2 SVD 的优势
SVD 无需对样本进行中心化处理,可直接对原始稀疏矩阵进行分解,完全保留稀疏特性。结合稀疏矩阵专用分解算法(如稀疏 SVD),能进一步降低存储与计算开销,适用于大规模稀疏数据场景。
4.3.3 工具包实践验证(以 Python scikit-learn 为例)
以 Python 机器学习库 scikit-learn 为例,二者的降维接口 fit_transform() 对输入数据类型的要求差异,直接反映了数据适应性的区别,
sklearn.decomposition.PCA 的 fit_transform() 操作:
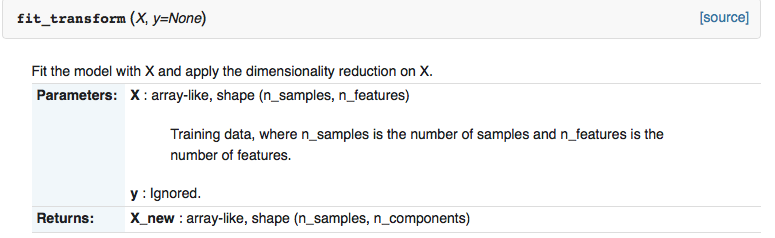
sklearn.decomposition.TruncatedSVD 的 fit_transform() 操作:

| 方法 | 输入数据类型支持 | 输出数据类型 |
|---|---|---|
sklearn.decomposition.PCA.fit_transform() | 仅支持稠密矩阵(array-like) | 稠密矩阵(array-like,shape=(n_samples, n_components)) |
sklearn.decomposition.TruncatedSVD.fit_transform() | 支持稠密矩阵(array-like)与稀疏矩阵(如 scipy.sparse.csr_matrix) | 稠密矩阵(array,shape=(n_samples, n_components)) |
该接口差异直接体现了 SVD 对稀疏数据的适应性优势,而 PCA 因中心化操作限制,无法处理稀疏输入。
4.4 应用场景细分(基于特性差异)
4.4.1 PCA 的典型场景
- 小规模稠密数据降维:如传统统计分析中的低维数据集(样本数与特征数均小于 10310^3103),计算协方差矩阵成本可控;
- 数据可视化:将高维数据降维至 2D/3D 空间(如手写数字数据集 MNIST 降维后可视化分类效果);
- 特征工程预处理:在分类/回归任务前,通过 PCA 去除冗余特征,减少模型训练时间。
4.4.2 SVD 的典型场景
- 大规模稀疏数据处理:如推荐系统的用户-物品评分矩阵(稀疏度通常 > 95%),通过 SVD 提取隐特征实现推荐;
- 图像压缩与去噪:将图像矩阵(m×nm \times nm×n)通过部分 SVD 近似,保留前 kkk 个大奇异值(过滤小奇异值对应的噪声),实现高效压缩;
(图 4:保留不同数量奇异值的图像效果,rrr 越小,压缩率越高,细节越少) - 线性方程组最小二乘求解:非方阵无逆矩阵,通过 SVD 求伪逆(A+=VΣ+UTA^+ = V\Sigma^+U^TA+=VΣ+UT,Σ+\Sigma^+Σ+ 为 Σ\SigmaΣ 非零奇异值取倒数后转置),用于数据拟合等场景。
五、数学基础:基变换(降维的逻辑)
无论是 PCA 还是 SVD,其降维本质都是“基变换”——将向量从原始正交基映射到新的正交基(主成分/奇异向量),因此需明确基变换的数学原理,确保前文方法的理论闭环。
5.1 基的要求:为何选择单位正交基?
基变换的目标是“无冗余且计算简便”,单位正交基(满足“两两正交+长度为 1”)是最优选择,原因如下:
5.1.1 非单位基的局限性
若基向量长度不为 1(如 (1,1)(1,1)(1,1),长度为 2\sqrt{2}2),则向量在该基上的投影需额外归一化(除以基长度),步骤繁琐且易引入误差。
5.1.2 单位正交基的优势:内积与投影直接关联
根据内积定义:对向量 A\boldsymbol{A}A 与单位基向量 B\boldsymbol{B}B(∣B∣=1|\boldsymbol{B}|=1∣B∣=1),有:
A⋅B=∣A∣⋅∣B∣⋅cosθ=∣A∣⋅cosθ\boldsymbol{A} \cdot \boldsymbol{B} = |\boldsymbol{A}| \cdot |\boldsymbol{B}| \cdot \cos\theta = |\boldsymbol{A}| \cdot \cos\thetaA⋅B=∣A∣⋅∣B∣⋅cosθ=∣A∣⋅cosθ
该结果恰好是 A\boldsymbol{A}A 在 B\boldsymbol{B}B 方向上的投影长度,即 A\boldsymbol{A}A 在以 B\boldsymbol{B}B 为基的坐标系中的坐标值。无需额外计算,通过内积即可直接得到新坐标,大幅简化运算。
5.2 基变换的数学实现:矩阵乘法
5.2.1 矩阵定义
设原始向量维度为 nnn,新基数量为 kkk(k≤nk \leq nk≤n),定义两个关键矩阵:
- 新基矩阵 P\boldsymbol{P}P:k×nk \times nk×n 矩阵,每行对应一个单位正交基向量(如二维空间中,新基 b1=(12,12)\boldsymbol{b}_1=(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})b1=(21,21)、b2=(−12,12)\boldsymbol{b}_2=(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})b2=(−21,21),则 P=[b1Tb2T]=[1212−1212]\boldsymbol{P}=\begin{bmatrix}\boldsymbol{b}_1^T\\\boldsymbol{b}_2^T\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix}P=[b1Tb2T]=[21−212121]);
- 样本矩阵 X\boldsymbol{X}X:n×mn \times mn×m 矩阵,每列对应一个待变换的原始向量(mmm 为样本数)。
5.2.2 坐标计算与几何意义
向量在新基下的坐标矩阵 X′\boldsymbol{X}'X′ 由矩阵乘法实现:
X′=P⋅X\boldsymbol{X}' = \boldsymbol{P} \cdot \boldsymbol{X}X′=P⋅X
-
几何意义 1:空间映射——将 X\boldsymbol{X}X 中所有向量,从原始基张成的空间,映射到新基 P\boldsymbol{P}P 张成的 kkk 维空间中;
-
几何意义 2:线性变换——矩阵 P\boldsymbol{P}P 代表“从原始坐标系到新坐标系”的线性变换,保持向量的线性关系(如加法、数乘)不变,仅改变坐标表示形式。
-
示例:原始向量 x=(3,2)\boldsymbol{x}=(3,2)x=(3,2)(样本矩阵 X=[32]\boldsymbol{X}=\begin{bmatrix}3\\2\end{bmatrix}X=[32]),经上述 P\boldsymbol{P}P 变换后:
X′=[1212−1212]⋅[32]=[52−12]\boldsymbol{X}' = \begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{bmatrix} \cdot \begin{bmatrix}3\\2\end{bmatrix} = \begin{bmatrix}\frac{5}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}\end{bmatrix}X′=[21−212121]⋅[32]=[25−21]
结果即 x\boldsymbol{x}x 在新基下的坐标,与内积计算结果完全一致(x⋅b1=52\boldsymbol{x} \cdot \boldsymbol{b}_1 = \frac{5}{\sqrt{2}}x⋅b1=25,x⋅b2=−12\boldsymbol{x} \cdot \boldsymbol{b}_2 = -\frac{1}{\sqrt{2}}x⋅b2=−21)。
六、总结:知识体系与逻辑闭环
-
概念层面:特征值是方阵的“专属特征”,描述线性变换的稳定方向与伸缩比例;奇异值是特征值的“广义推广”,突破方阵限制,适用于任意矩阵,通过“矩阵-转置乘积的特征值平方根”定义。
-
分解层面:实对称方阵的特征值分解(A=QΛQTA=Q\Lambda Q^TA=QΛQT)是 PCA 的核心;任意矩阵的 SVD(A=UΣVTA=U\Sigma V^TA=UΣVT)是矩阵近似、压缩的基础,且可间接实现 PCA,效率更高。
-
应用层面:PCA 适用于小规模稠密数据降维;SVD 适用于大规模稀疏数据处理、图像压缩、推荐系统等场景,应用范围更广。
-
数学基础:基变换是降维的本质,单位正交基通过“内积=投影”简化计算,是 PCA 选择主成分、SVD 选择奇异向量的核心依据。
via:
-
1 Singular Value Decomposition and Principal Component Analysis - 180lecture_svd_pca.pdf
https://math.ucdavis.edu/~strohmer/courses/180BigData/180lecture_svd_pca.pdf -
特征值和奇异值的关系_奇异值与特征值的关系-CSDN 博客 Never-Giveup 于 2018-08-25 16:40:40 发布
https://blog.csdn.net/qq_36653505/article/details/82052593 -
特征值与奇异值的基础知识 - litaotao_doctor - 博客园 posted on 2016-03-26 17:08 litaotao_doctor
https://www.cnblogs.com/litaotao-doctor/p/5320521.html -
降维方法 PCA 与 SVD 的联系与区别 - Byron_NG - 博客园
https://www.cnblogs.com/bjwu/p/9280492.html- Reference
- 《线性代数及其应用》. David C Lay
- 奇异值分解 (SVD) 原理详解及推导_svd 分解-CSDN 博客
https://blog.csdn.net/zhongkejingwang/article/details/43053513 - 数据分析中的降维方法初探 - 郑瀚 - 博客园
http://www.cnblogs.com/LittleHann/p/6558575.html - 奇异值分解 (SVD) 原理与在降维中的应用 - 刘建平 Pinard - 博客园
https://www.cnblogs.com/pinard/p/6251584.html - PCA 与 SVD 解析-CSDN 博客
https://blog.csdn.net/wangjian1204/article/details/50642732 - 《机器学习》. 周志华
- Reference
… …
