复杂结构数据挖掘(二)关联规则挖掘 Association rule mining
你是否曾好奇,为什么超市总把啤酒和尿布摆在一起?这看似随意的陈列背后,藏着数据挖掘领域的经典智慧 —— 关联规则挖掘。在大数据时代,海量交易记录如同未开垦的金矿,而关联规则正是撬开这座金矿的关键工具。想象一下,当你在电商平台浏览商品时,系统推荐的 "买了这个的人还买了...",或是超市根据消费数据优化的货架布局,这些场景背后都离不开关联规则算法的神奇魔力。
从本质上讲,关联规则挖掘要解决的核心问题,是在庞大的交易数据中找出 "X→Y" 这样的隐含关系 —— 例如 "买了面包的人更可能买牛奶"。但面对动辄百万级的商品和交易记录,直接暴力枚举所有可能的商品组合显然不现实。这就像在沙滩上寻找特定形状的贝壳,若没有高效的工具,终将被海量数据淹没。于是,Apriori、FP-growth 等经典算法应运而生,它们如同数据海洋中的导航仪,通过巧妙的剪枝策略和数据结构优化,让我们能在合理时间内挖掘出有价值的规则。
从 Apriori 利用 "频繁项集的子集必频繁" 的先验知识进行剪枝,到 DHP 算法引入哈希技术加速候选集筛选;从 FP-growth 通过构建 FP 树实现 "两次扫描数据库即可挖矿" 的高效操作,到 Closed/Maxinal 频繁项集实现的信息精简表示。我们还将登上多层关联规则和多维关联规则的瞭望塔,俯瞰如何在不同概念层级和多维度数据中挖掘隐藏模式,最后还要警惕关联规则可能的 "陷阱"—— 那些看似强大却缺乏实际价值的虚假关联。
目录
1. 关联规则问题的基本定义
2. Apiriori 算法 合并+筛选
2.1 算例
3. DHP 算法 -- 散列表哈希+剪枝
第 1 次扫描:生成 L1 并为 C2 构建散列表
在第 1 次和第 2 次扫描之间:生成剪枝后的 C2
4. FP-growth 频繁模式增长 FP-tree
5. Closed / Maxinal frequent itemset
6. 多层关联规则挖掘 Mining multilevel association rules
6.1 不同的层级策略:
6.2 Redundancy filtering 冗余过滤
7. 多维关联规则挖掘
8. 关联规则 本身可能的问题
1. 关联规则问题的基本定义
给定:
-
一个交易数据集 T(例如,所有购物小票的集合)。
-
一个物品的集合
I(例如,超市中所有商品的集合)。 -
用户自定义的最小支持度阈值
min_sup和最小置信度阈值min_conf。
找出:
所有满足以下条件的关联规则 X -> Y(其中 X 和 Y 都是物品集 I 的子集,且 X ∩ Y = ∅):
-
支持度条件: 规则的支持度 XY一起出现的概率 P(XY) =
support(X -> Y)≥min_sup。-
目的: 确保规则所描述的模式在数据集中是普遍存在的,不是偶然事件。
-
-
置信度条件: 规则的置信度 P(Y|X) =
confidence(X -> Y)≥min_conf。-
目的: 确保规则是可靠的,即当前件
X出现时,后件Y也有很高的概率出现。
-
大规模数据集(如超市数据)难点:物品太多 -> 候选子集太多了;
数支持度和置信度 需要扫描数据库 也耗时。
2. Apiriori 算法 合并+筛选
一个频繁项集的所有子集也一定是频繁的。(加入元素后 出现次数一定非递增)
只能用频繁项集生成更大的频繁项集。
1. 合并生成操作:两个k项集 拼成一个k+1项集(这两个本来只有一个不一样)
2. 筛选:新得到的 k+1项 所有k子项都得频繁。 (新的 k+1 去掉任何一个后都频繁)
通过这个必要条件筛选后,再去计算 这个k+1项的支持度和置信度。
第一轮 筛单项,后续先组合+筛,再数一下判断。
2.1 算例
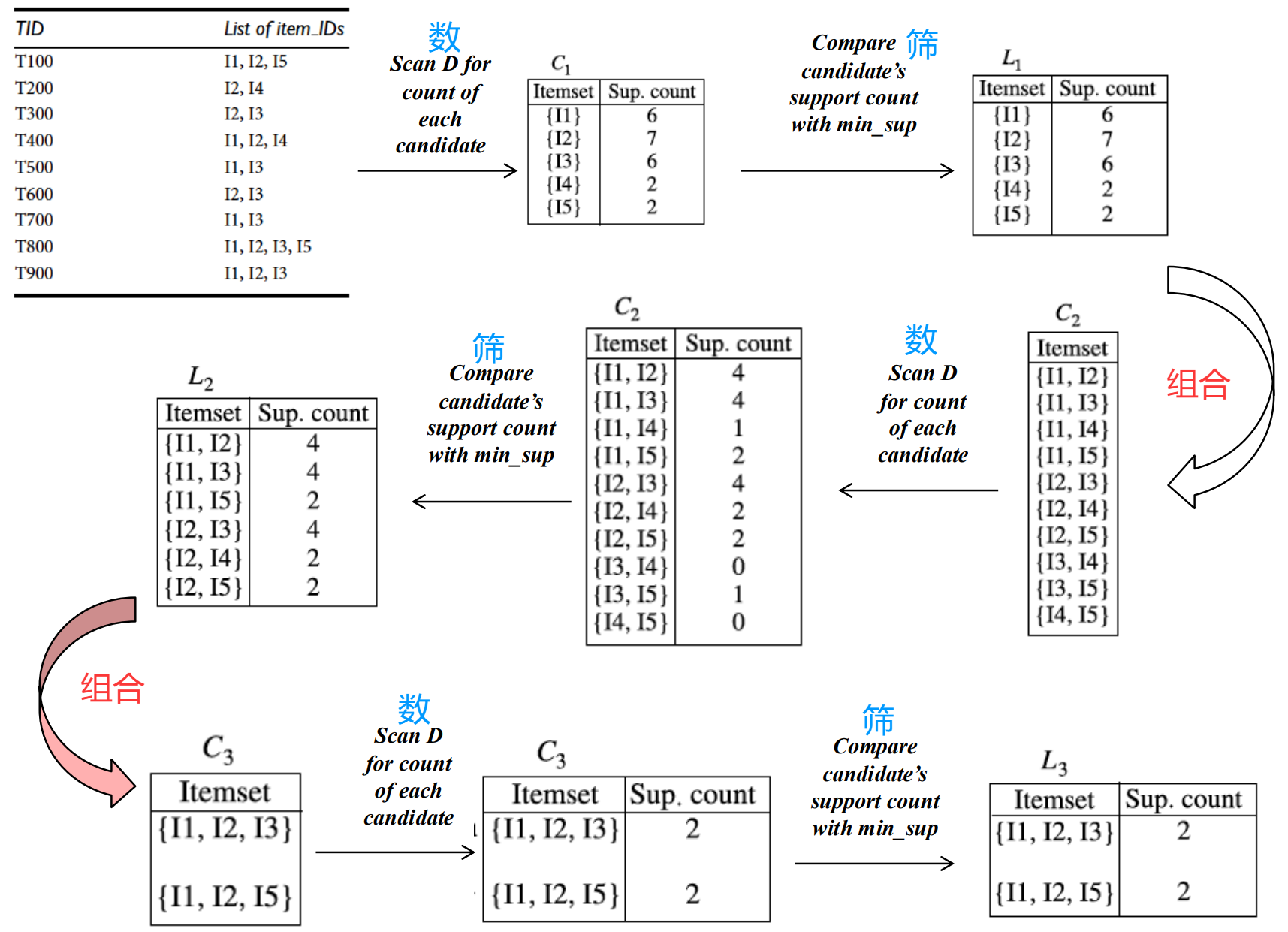
在第二次组合中,虽然 12 24 都在 但因为14不频繁,所以124无法成团。
要124 出现次数 ≥ 2;必要条件 12 24 14 都出现次数 ≥ 2。
ApirioriTid 空间换时间,后续不扫描整个数据库
额外拉一个数据结构:对每笔交易 存频繁k项集 有哪些
3. DHP 算法 -- 散列表哈希+剪枝
Direct Hashing and Pruning 使用散列表直接定位 和 基于散列桶计数进行早期修剪。
Apriori 算法的瓶颈:
由频繁 2-项集(L2)生成候选 3-项集(C3)时,候选集数量会呈组合爆炸式增长。
需要多次扫描整个数据库,并对海量候选集进行支持度计数,耗时太多。
加上了散列表构建和剪枝的操作:
第 1 次扫描:生成 L1 并为 C2 构建散列表
-
计数:扫描数据库
D,统计每个单项的支持度,生成频繁 1-项集L1。 -
为 C2 构建散列表(关键步骤):
-
散列函数:选择一个散列函数,例如:
hash({x, y}) = ((x的序号) * 10 + (y的序号) ) mod n,其中n是散列表的大小(桶的数量)。 -
操作:对于交易
T中每一个可能的 2-项集{i, j}(其中 i < j),计算其散列值h,然后将散列表中第h个桶的计数值加 1。 -
目的:这个散列表的每个桶的计数,代表了有多少个交易包含了会映射到这个桶的所有 2-项集。“桶支持度”是高于单体支持度的,在后面的筛选中,如果项集映射的桶支持度都低于阈值,单种类项集一定就低于阈值。
-
在第 1 次和第 2 次扫描之间:生成剪枝后的 C2
-
生成初始 C2:通过
L1自连接,生成所有可能的候选 2-项集C2_candidate。 -
散列剪枝:
-
对于
C2_candidate中的每一个候选 2-项集c,计算对应桶的计数。 -
修剪规则:如果桶的计数 < min_sup,那么意味着即使把所有映射到这个桶的项集都算上,它们的总支持度也达不到最小支持度。因此,这个桶里的任何一个具体的候选集
c都绝对不可能是频繁的。 就把这个候选 pass掉。
-
后续流程类似:
-
扫描数据库,统计剪枝后的
Ck的支持度,生成频繁集Lk。 -
在扫描的同时,可以为
C{k+1}构建散列表(并应用事务裁剪:只处理项数 >= k+1 的交易)。 -
利用新构建的散列表对下一步生成的
C{k+1}进行剪枝。
4. FP-growth 频繁模式增长 FP-tree
-- 之前方法的两个问题:
在CPU上处理比较快,但是扫描数据库(验证这个组合符不符合)太耗时了;
上两种方法 generation-and-test 的范式,丢失了很多生成信息。
-- 能否只扫描数据库两次,就将整个数据库压缩成一棵高度浓缩的数据结构 FP-tree,然后在这棵树上进行“挖矿”,完全避免产生候选集?
先根据 单项的 frequent 信息,对每个T 交易的每样物品进行排序,并删掉不频繁的单项。
如何表征 商品出现在一个购物车里? 建树的时候串起来。
由于排序过 实现了共享前缀,自底向上拎起来 就是这一组的出现次数。
建树过程有点像字典树:
对单项:数 + 留频繁 + 排序
每个交易小票 transaction:根连着首项,接着后一个,如果没有就开一个新后继。节点计数+1。
对同一个字母 前后用链串起来方便后续检索。
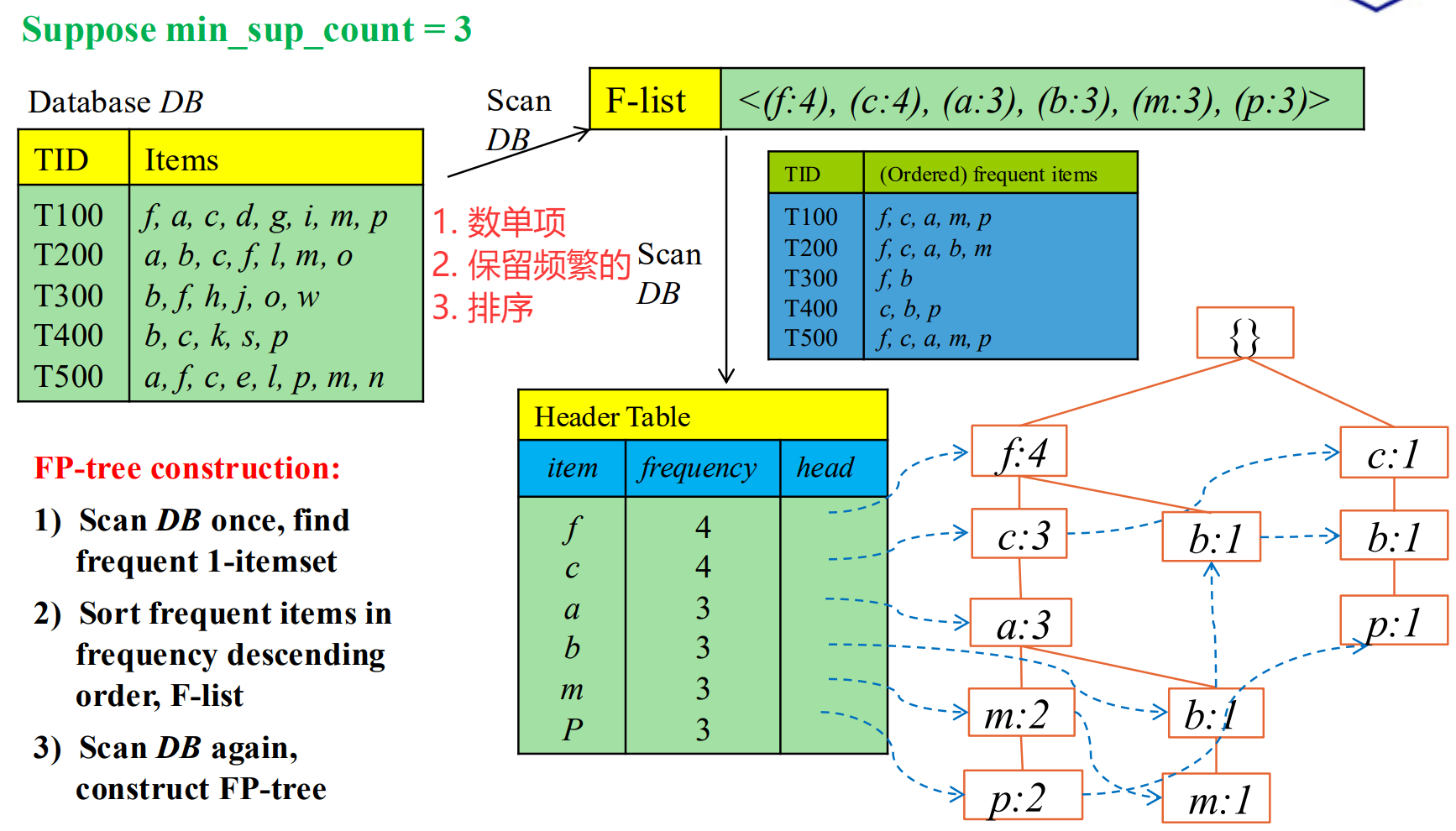
如何产生频繁项集:
1. 先选一个开始的项(后面算带这个项的 所有频繁的)
2. 通过项 X 的节点链,收集所有包含 X 的前缀路径。
每一条从根节点到 X 的父节点的路径,就是 X 的一个条件模式基。
如果路径 A->B->C 指向 X:2,那么这条条件模式基就是 {A, B, C}:2。
要找带 m 的串,沿着m的链,往上找前缀:
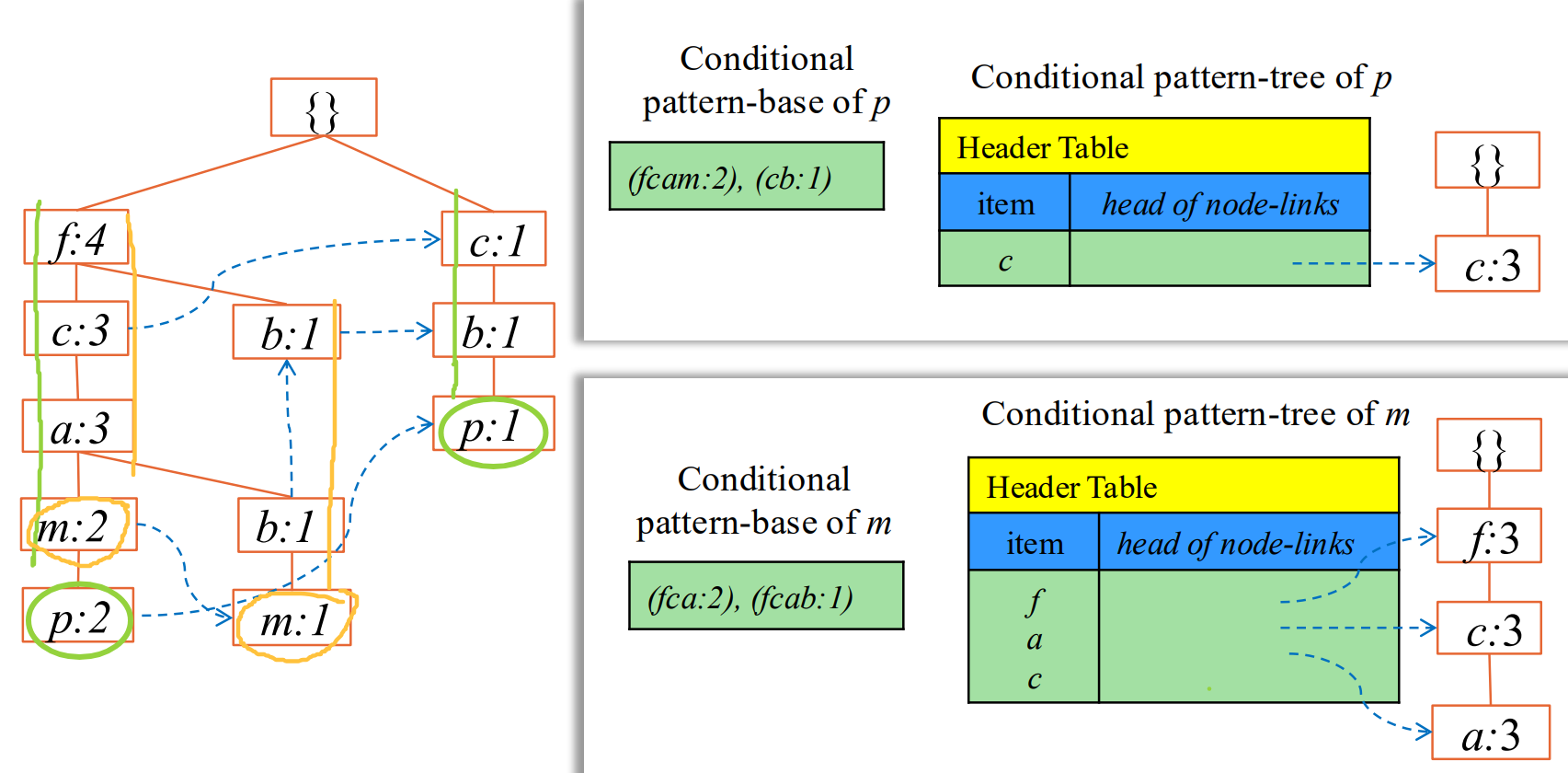
把前缀统计合并,带 m 的频繁集,只需对前缀进行 0-1 选取。
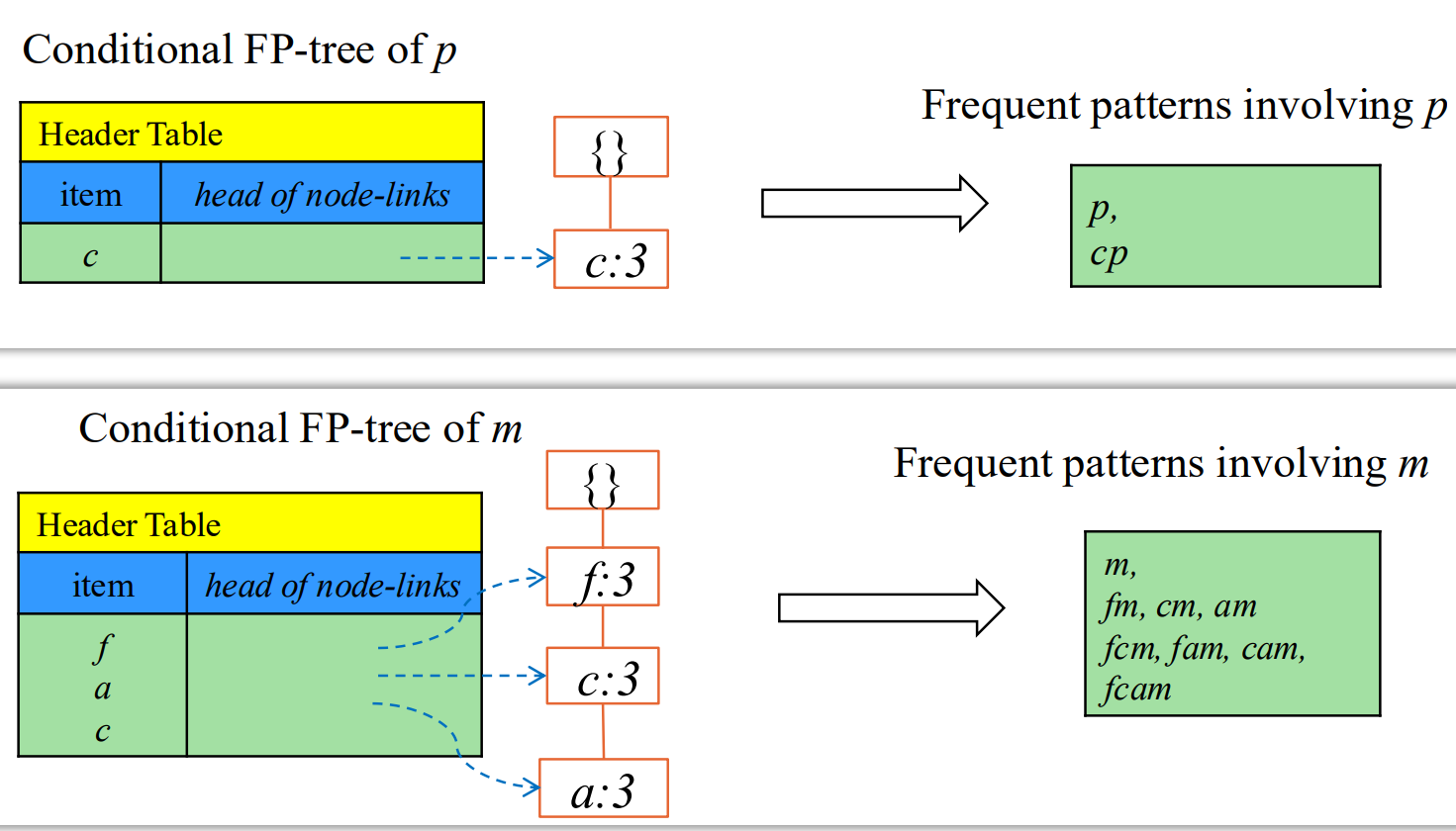
优化技巧:从中间分治 先做上面的,再把上面作为一个整体节点。
合并:集合乘法;前面选几个,后面选几个
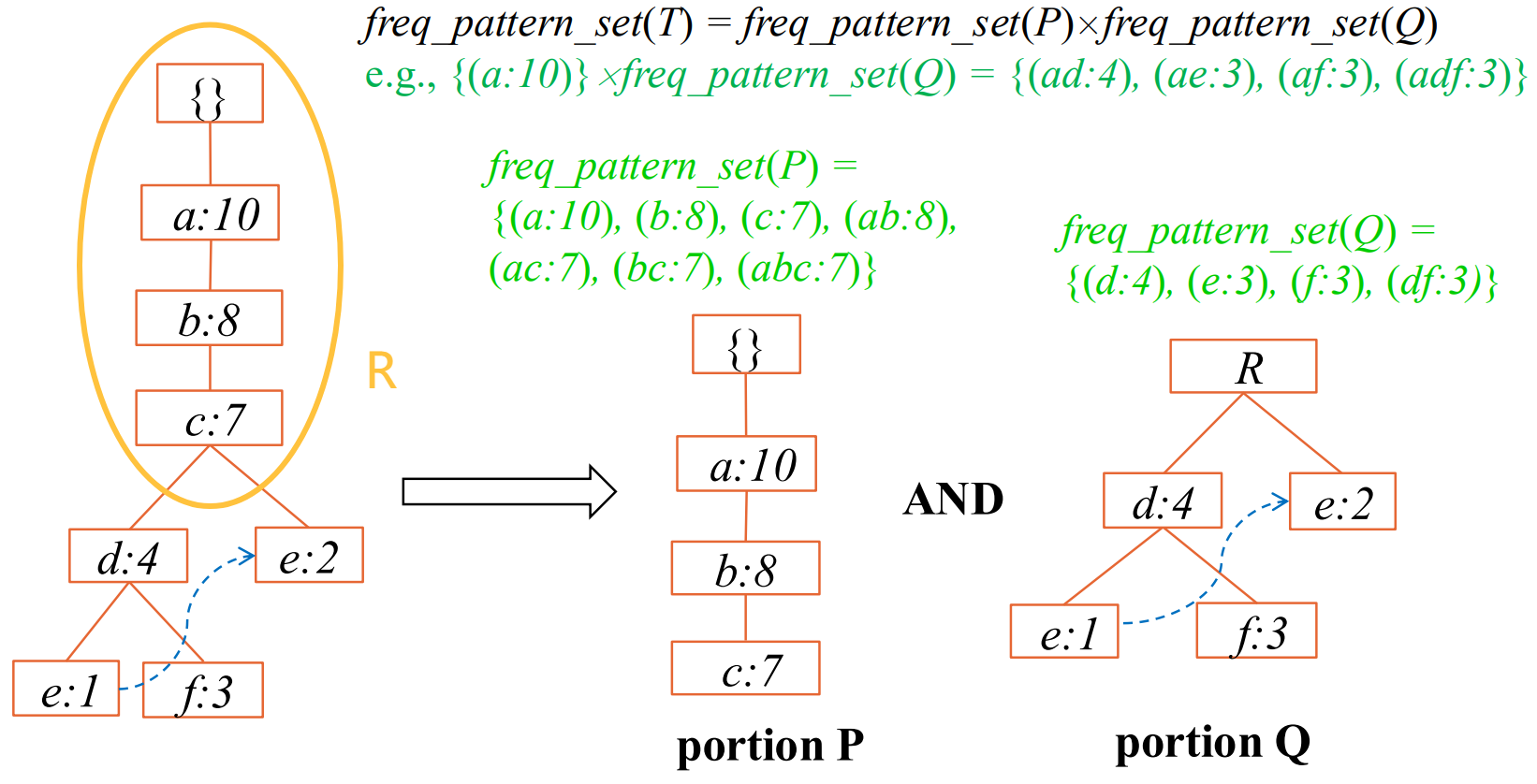
例2:min_sup=2
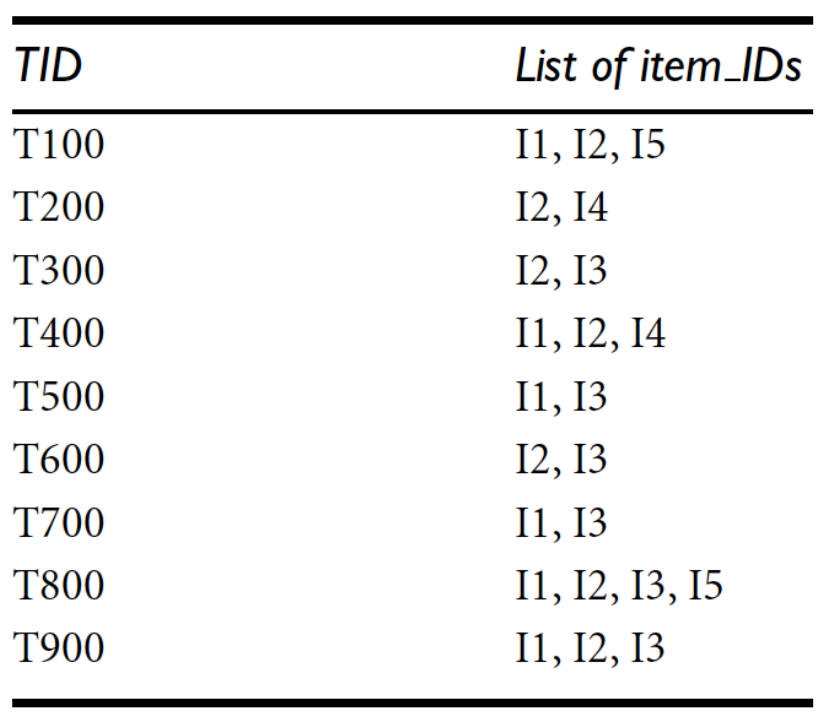
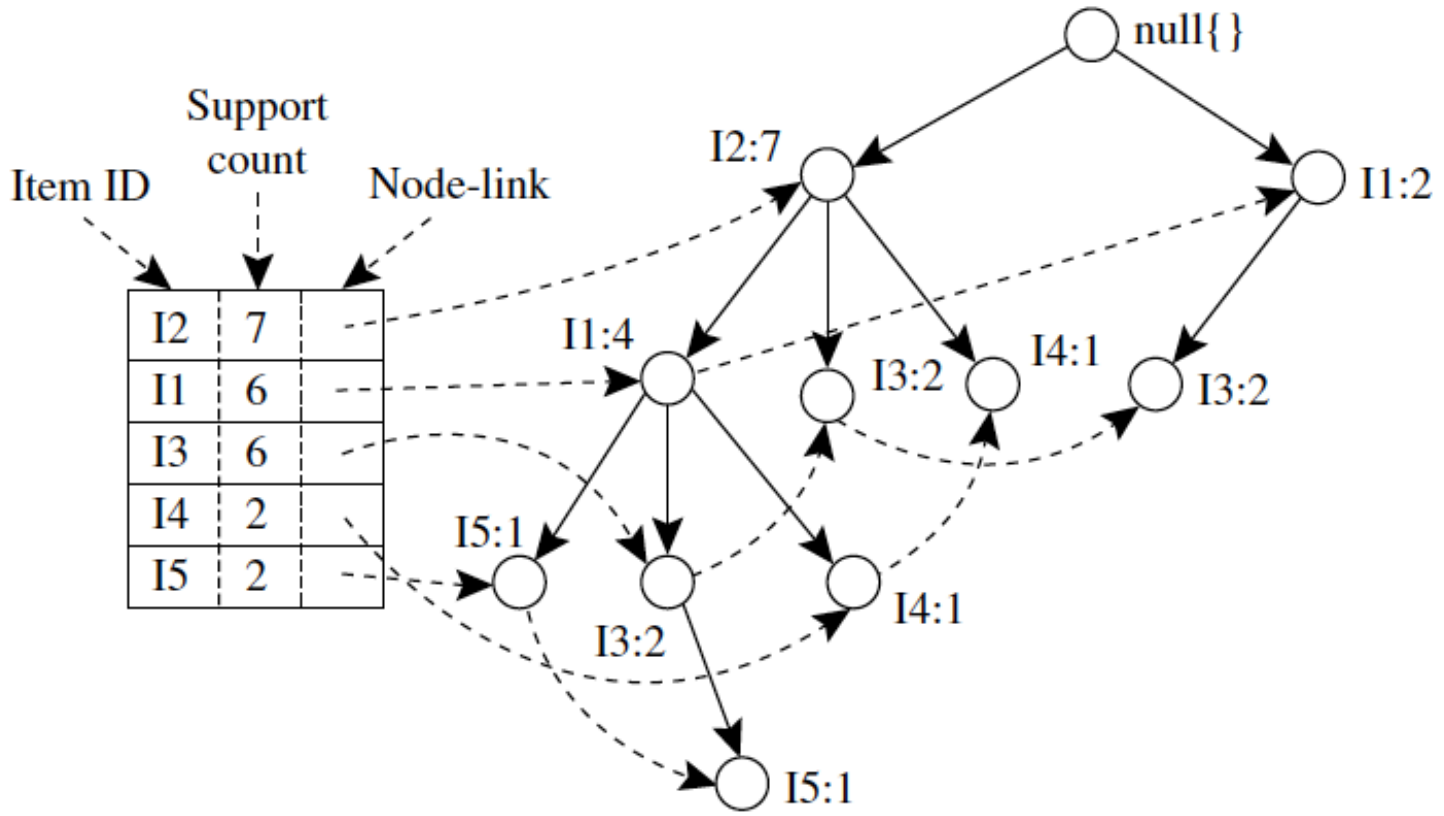
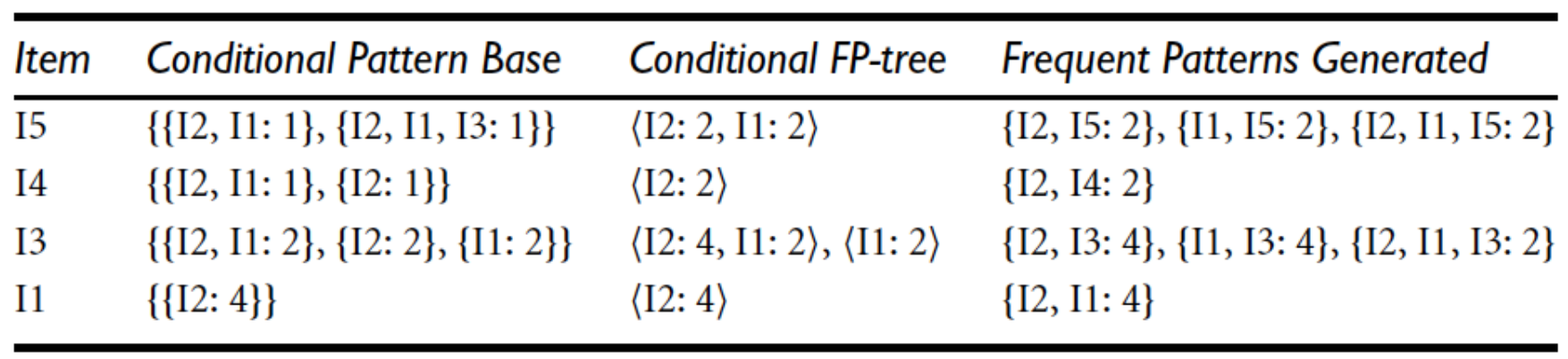
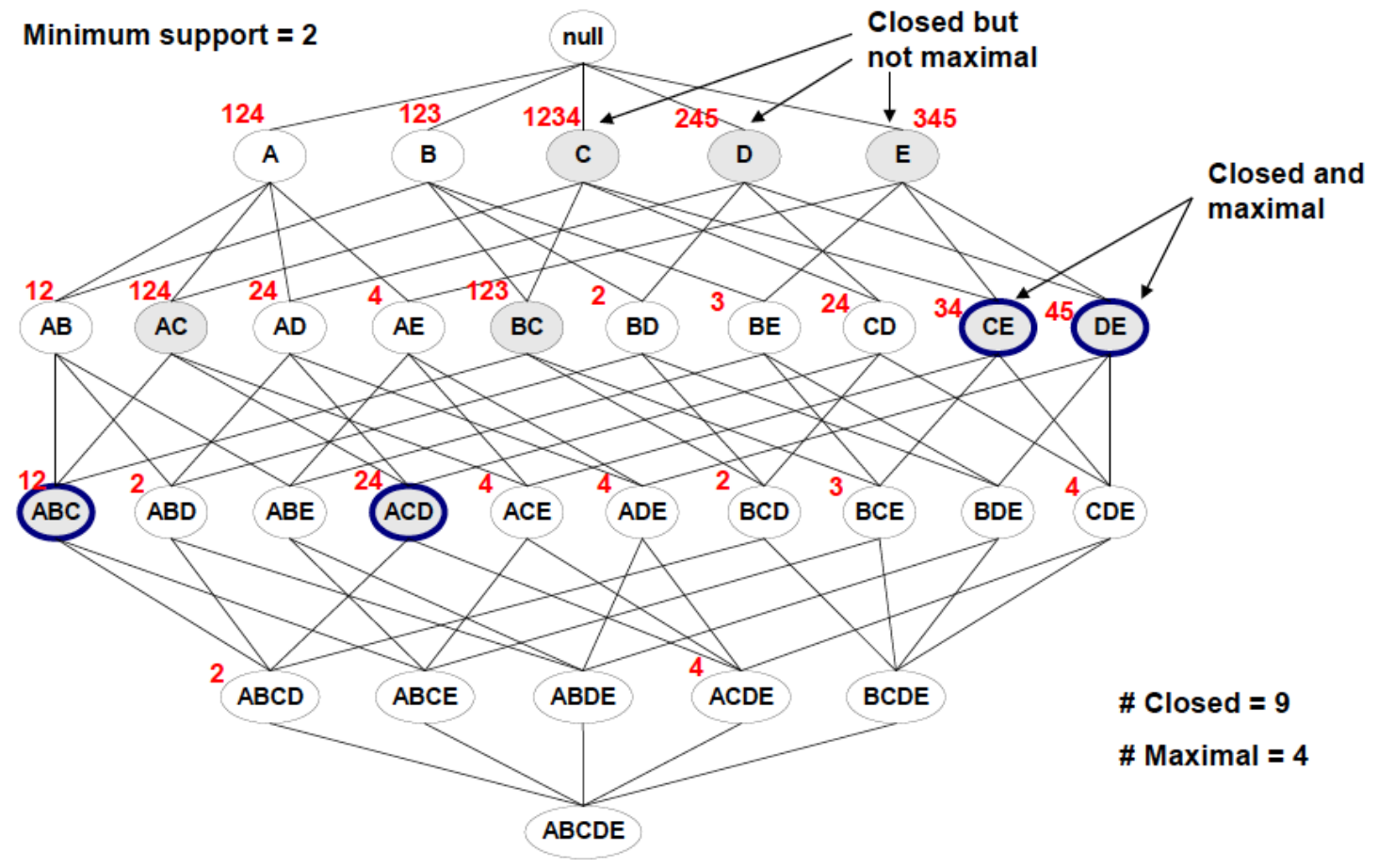
5. Closed / Maxinal frequent itemset
一个 N-频繁项集的所有 2^N - 1 个子集 全都是频繁的。
我们不需要把 它的这些子集全都挖掘出来,这个 N-频繁项集 已经包含了全部的信息。
精简表示 -> 最少保存多少信息 就可以知道全部的信息呢?
Closed:加任何元素之后,支持度都会下降。
Maxinal:再塞元素就不频繁了。(包含于Closed)
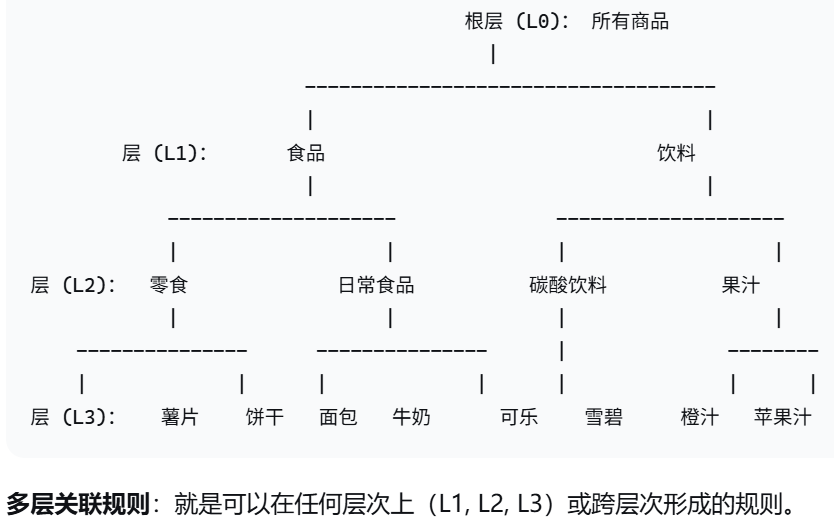
6. 多层关联规则挖掘 Mining multilevel association rules
Concept Hierarchies(概念层次结构) 进行规则泛化的尺度。(不同层次商品)
啤酒与尿布显著,但某种啤酒和某种尿布 不一定显著。
小朋友喜欢吃KFC 泛化到人喜欢吃饭 还有没有意义。
不是每层分开算 利用不同层次之间关系。
6.1 不同的层级策略:
| 方法类别 | 核心判断依据 | 优势 | 劣势 |
|---|---|---|---|
| 逐层独立 | 不考虑父节点是否频繁,所有节点都检查 | 不遗漏关联 | 检查大量无用(不频繁、不重要)项 |
| 基于k项集的跨层过滤 | 父k项集频繁,才检查子k项集 | 只关注频繁项的子项,减少无效检查 | 可能漏掉有价值但父项集不频繁的模式 |
| 基于单个项的跨层过滤 | 父节点(单个项)频繁,才检查子节点 | 平衡 “全检查” 和 “只查频繁父项集子项” | 可能漏掉父节点不频繁、但自身(子项)在低支持度下频繁的关联 |
| 受控的基于单个项的跨层过滤 | 父项满足 “层级传递阈值”(非严格最小支持度),则子项可被检查 | 放宽限制,让更多潜在项有被检查的可能 | 阈值设置难度大,不好把控 |
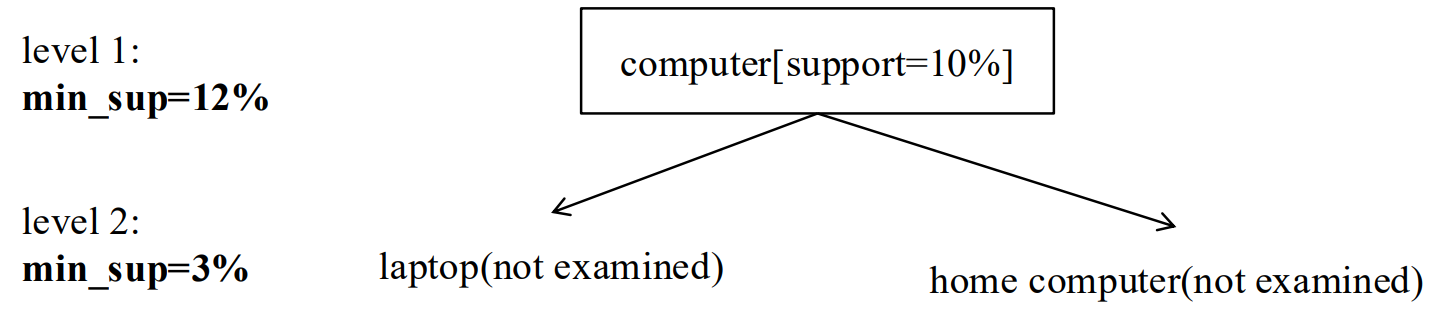
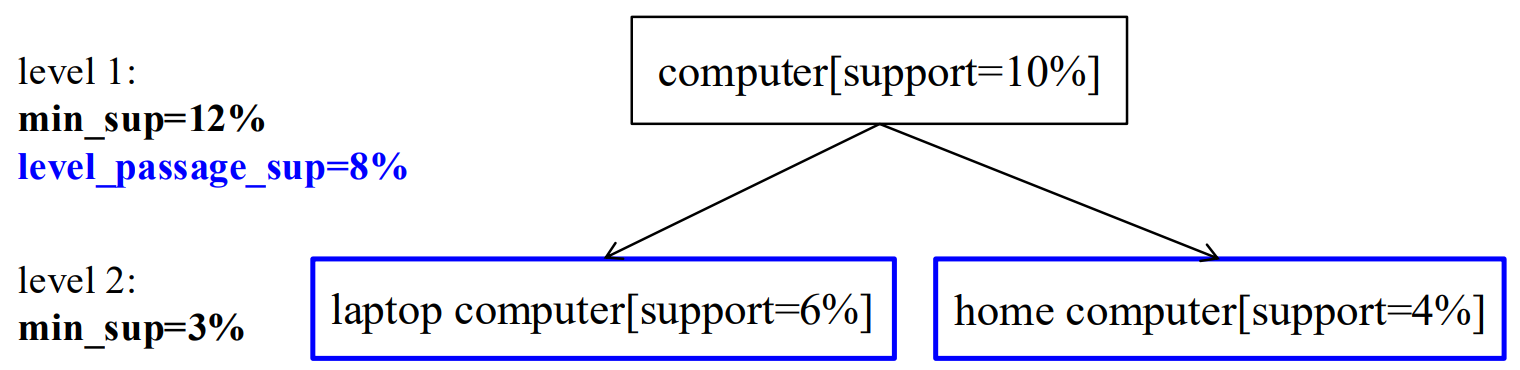
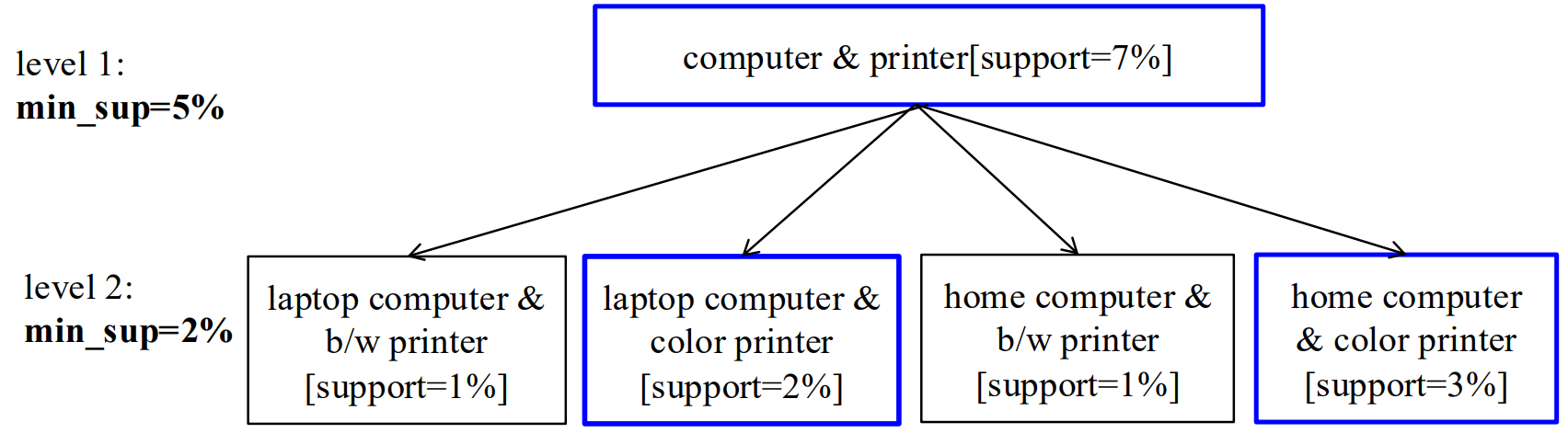
6.2 Redundancy filtering 冗余过滤
有意义的规则(去除冗余 有不一样)
祖先(规则层面):如果规则R1可以通过将规则R2中的项替换为它们在概念层次结构中的祖先项而得到,那么规则R1就是规则R2的祖先。
如果一条规则的支持度和置信度与其祖先规则的 “预期” 支持度和置信度接近,那么这条规则可以被认为是冗余的。
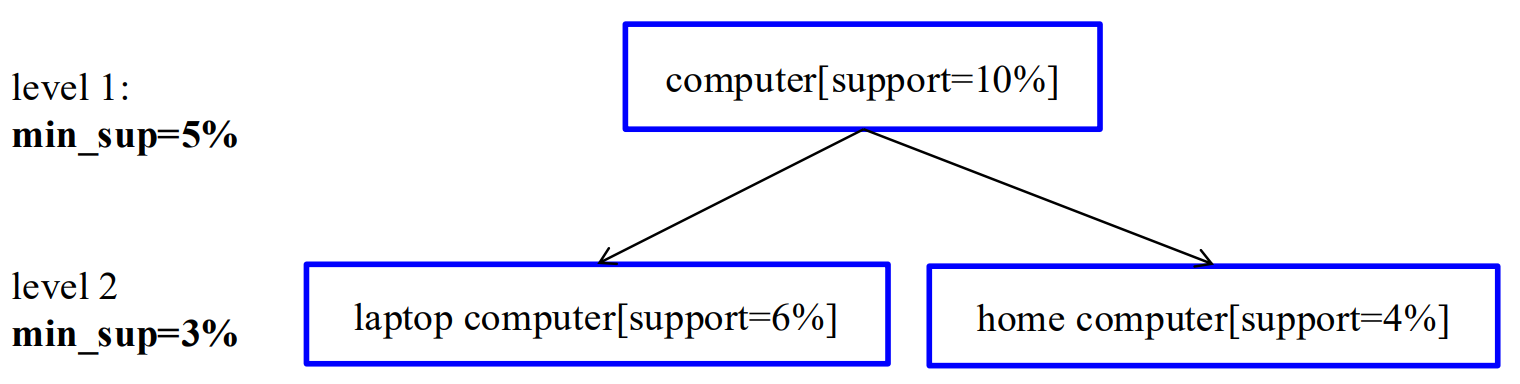
例如:若 IBM computer -> HP printer 与 computer -> HP printer 按比例缩放
那么是不是 IBM电脑 对HP打印机没有影响,记录这条规则就是冗余的。
如果发现 买 IBM电脑的人 相较于整体买电脑的人,买HP打印机远远少,这个额外信息就是有作用的。
7. 多维关联规则挖掘
单维度: IBM 电脑 -> HP 打印机
多维度: IBM 电脑 + 20-24岁 -> HP 打印机 (前面多变量影响)
多维关联规则挖掘寻找的是频繁谓词集(前面k个指标组合)。
如果有很多购物记录都同时满足P1^P2^P3(即“年龄20-30岁、收入超5000元、买了笔记本电脑”),那么谓词集{P,P2,P3}就是一个频繁谓词集。
数值型属性动态离散化:分箱 + 找频繁 + 聚类合并
8. 关联规则 本身可能的问题
例:60%买游戏 75%买光盘 40%都买 66%买游戏的买了光盘,
那么 买游戏 -> 买光盘 (40%,66%)达到了支持度和置信度。(按之前 这符合关联规则)
但是实际上 66% < 75% 买游戏反而对买光盘产生了负面作用。
置信度降低了,但仍然高于阈值。
Criticism: Strong association rules may not be interesting 符合要求 但不有趣(没用)
定义提升率:条件概率 除以 本来概率,和1比 是促进还是抑制。

