当前位置：首页 > news >正文

心痛之窗：滑动窗口算法解爱与愁的心痛（洛谷P1614）

news 2025/10/10 11:53:22

题目背景与情感共鸣

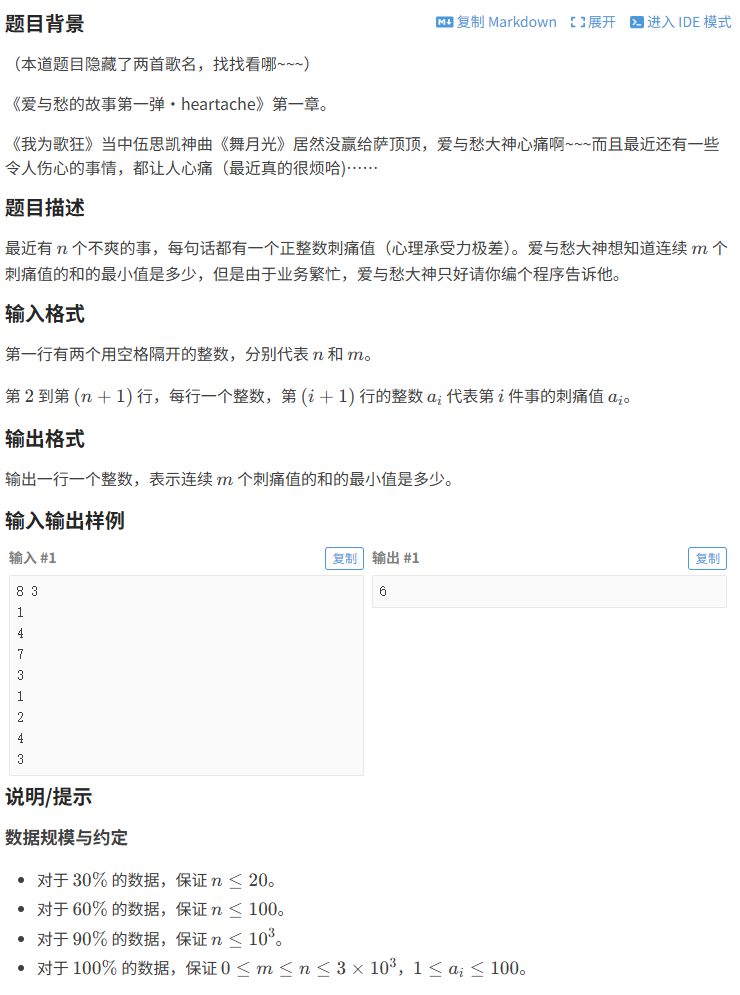
这道名为"爱与愁的心痛"的题目，巧妙地将情感主题与算法问题相结合。题目背景引用了《爱与愁的故事》和《我为歌狂》中的情节，营造出一种青春伤感的情感氛围。而算法核心则是寻找连续子数组的最小和，这种"心痛"的量化表达让人印象深刻。

问题分析

题目要求

给定一个包含n个正整数的序列（刺痛值），要求找出连续m个数字的和的最小值。

输入输出示例

输入：
8 3
1
4
7
3
1
2
4
3输出：
6

解释：连续3个刺痛值的最小和是1+2+3=6（对应第5、6、7个数字）

解题思路详解

核心算法：滑动窗口（Sliding Window）

滑动窗口算法是解决这类连续子数组问题的经典方法。其核心思想是维护一个固定大小的窗口，在数组上滑动，避免重复计算。

算法步骤

初始化窗口：计算前m个数字的和作为初始窗口和
滑动窗口：每次向右移动一位，减去离开窗口的数字，加上新进入窗口的数字
更新最小值：在滑动过程中记录遇到的最小和
边界处理：处理m=0的特殊情况

C++代码实现

基础版本：清晰易懂

#include <iostream>
#include <vector>
#include <climits> // 用于INT_MAX
using namespace std;int main() {int n, m;cin >> n >> m;vector<int> pain(n);for (int i = 0; i < n; i++) {cin >> pain[i];}// 处理m=0的特殊情况if (m == 0) {cout << 0 << endl;return 0;}// 初始化第一个窗口的和int current_sum = 0;for (int i = 0; i < m; i++) {current_sum += pain[i];}int min_sum = current_sum;// 滑动窗口for (int i = m; i < n; i++) {current_sum = current_sum - pain[i - m] + pain[i];if (current_sum < min_sum) {min_sum = current_sum;}}cout << min_sum << endl;return 0;
}

优化版本：处理边界更完善

#include <iostream>
#include <vector>
#include <climits>
using namespace std;int main() {int n, m;cin >> n >> m;// 边界情况处理if (n == 0 || m == 0) {cout << 0 << endl;return 0;}vector<int> pain(n);for (int i = 0; i < n; i++) {cin >> pain[i];}// 如果m大于n，实际上只能取n个连续数字int window_size = min(m, n);int current_sum = 0;// 计算第一个窗口for (int i = 0; i < window_size; i++) {current_sum += pain[i];}int min_sum = current_sum;// 滑动窗口处理剩余部分for (int i = window_size; i < n; i++) {current_sum += pain[i] - pain[i - window_size];min_sum = min(min_sum, current_sum);}cout << min_sum << endl;return 0;
}

单次遍历版本：极致简洁

#include <iostream>
#include <vector>
#include <climits>
using namespace std;int main() {int n, m;cin >> n >> m;vector<int> pain(n);for (int i = 0; i < n; i++) {cin >> pain[i];}if (m == 0) {cout << 0 << endl;return 0;}int current_sum = 0, min_sum = INT_MAX;for (int i = 0; i < n; i++) {current_sum += pain[i];// 当窗口大小达到m时开始滑动if (i >= m - 1) {min_sum = min(min_sum, current_sum);current_sum -= pain[i - m + 1];}}cout << min_sum << endl;return 0;
}

关键知识点深度解析

1. 滑动窗口算法（⭐⭐⭐⭐⭐）

核心思想：维护固定大小的窗口，避免重复计算
时间复杂度：O(n)，只需遍历数组一次
空间复杂度：O(1)，只使用常数个额外变量

2. 边界条件处理（⭐⭐⭐⭐）

m=0情况：连续0个数字的和为0
m>n情况：实际窗口大小应为min(m,n)
数组为空：n=0时的特殊处理

3. 算法优化技巧（⭐⭐⭐）

提前终止：如果当前和已经很大，可以提前判断
最小值更新：使用min函数简化代码
变量复用：重复使用current_sum变量

测试用例与验证

标准测试用例

// 测试用例1：题目样例
输入：8 31 4 7 3 1 2 4 3
输出：6// 测试用例2：边界情况
输入：5 01 2 3 4 5
输出：0// 测试用例3：全相同数字
输入：4 25 5 5 5
输出：10// 测试用例4：递增序列
输入：5 31 2 3 4 5
输出：6

性能测试

根据数据规模分析：

n ≤ 20：任何算法都能轻松处理
n ≤ 1000：滑动窗口算法优势明显
n ≤ 3000：滑动窗口仍然高效（3000次操作）

常见错误与解决方法

错误1：窗口大小处理不当

// 错误：未处理m>n的情况
for (int i = 0; i < m; i++) { // 如果m>n会越界current_sum += pain[i];
}

解决：

int window_size = min(m, n);
for (int i = 0; i < window_size; i++) {current_sum += pain[i];
}

错误2：索引计算错误

// 错误：索引计算偏差
current_sum = current_sum - pain[i - m] + pain[i];
// 当i=m时，i-m=0，正确

错误3：最小值初始化错误

// 错误：初始化为0
int min_sum = 0; // 如果所有和都大于0，会得到错误结果// 正确：初始化为极大值
int min_sum = INT_MAX;

竞赛技巧总结

识别滑动窗口模式：当问题涉及连续子数组时考虑此算法
边界测试优先：先处理m=0, n=0等边界情况
代码简洁性：使用标准库函数简化代码（如min, max）
提前优化：根据数据范围选择合适算法

实际应用拓展

滑动窗口算法在以下场景有广泛应用：

1. 数据流处理

// 实时数据流中的滑动平均值
class MovingAverage {
private:queue<int> window;int size;double sum;
public:MovingAverage(int size) : size(size), sum(0.0) {}double next(int val) {if (window.size() == size) {sum -= window.front();window.pop();}window.push(val);sum += val;return sum / window.size();}
};

2. 字符串处理

// 最长无重复字符子串
int lengthOfLongestSubstring(string s) {vector<int> charIndex(256, -1);int maxLength = 0, left = 0;for (int right = 0; right < s.length(); right++) {if (charIndex[s[right]] >= left) {left = charIndex[s[right]] + 1;}charIndex[s[right]] = right;maxLength = max(maxLength, right - left + 1);}return maxLength;
}