【22.1-决策树的构建1】

22.1 衡量示例集的纯度

一组猫和狗的照片作为示例集， 三只猫三只狗；

使用熵函数来测量示例集的不纯度

熵函数 H(p1)

纵轴代表熵的值，横轴代表示例中猫的比例 p1

当示例集中有三只猫和三只狗时，认为不纯度最高，熵最高，H = 1；而当示例集中全为猫/狗时，纯度最高，H = 0；

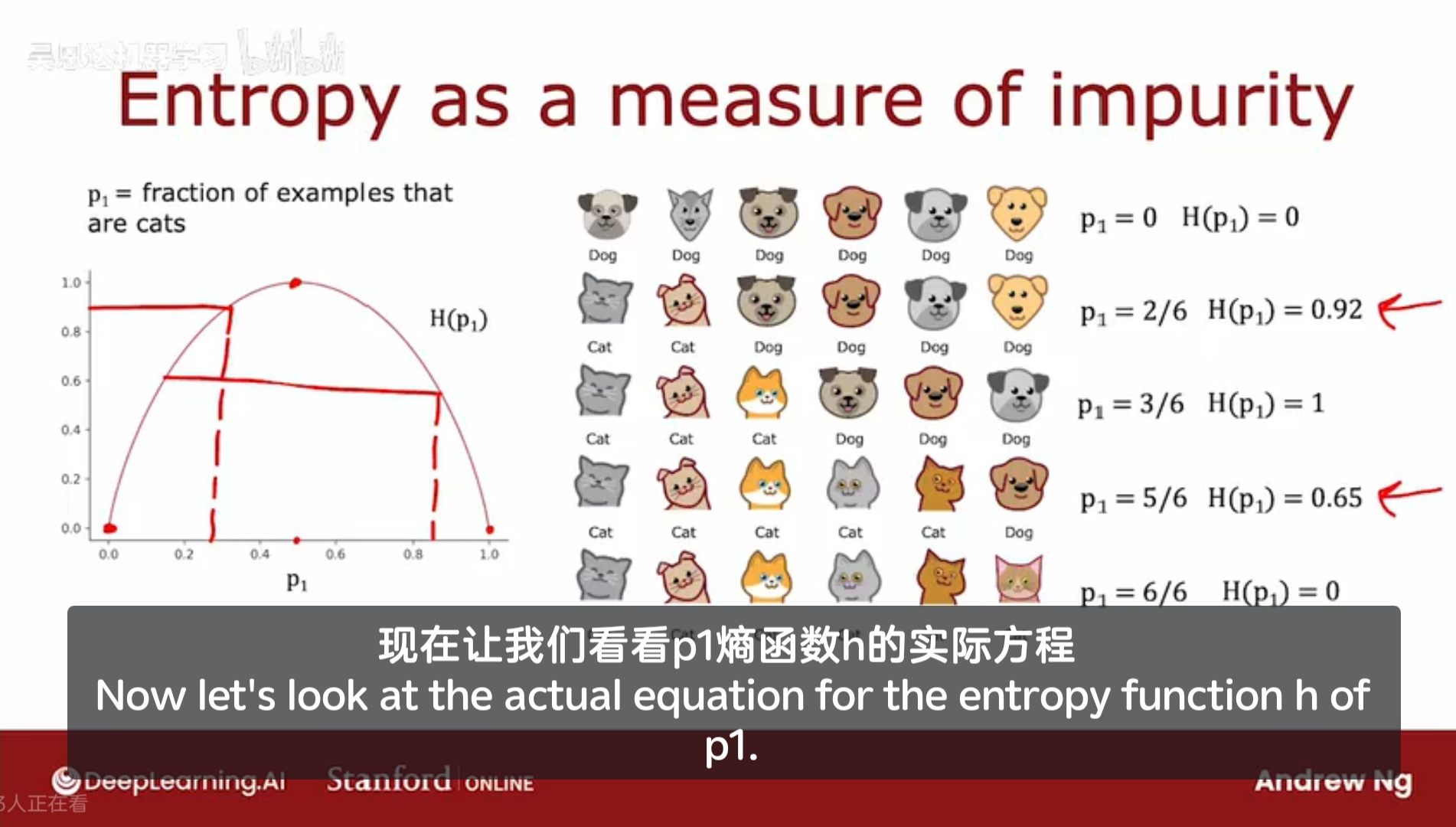
第二个示例集，五只猫和一只狗，则p1，即正例所占的比例，标记为1的例子所占的份额为5/6，则对应的 H = 0.65；

惯例上，计算熵时，使用的底数是2而不是e。取2为底数是为了使得该曲线的峰值为1；

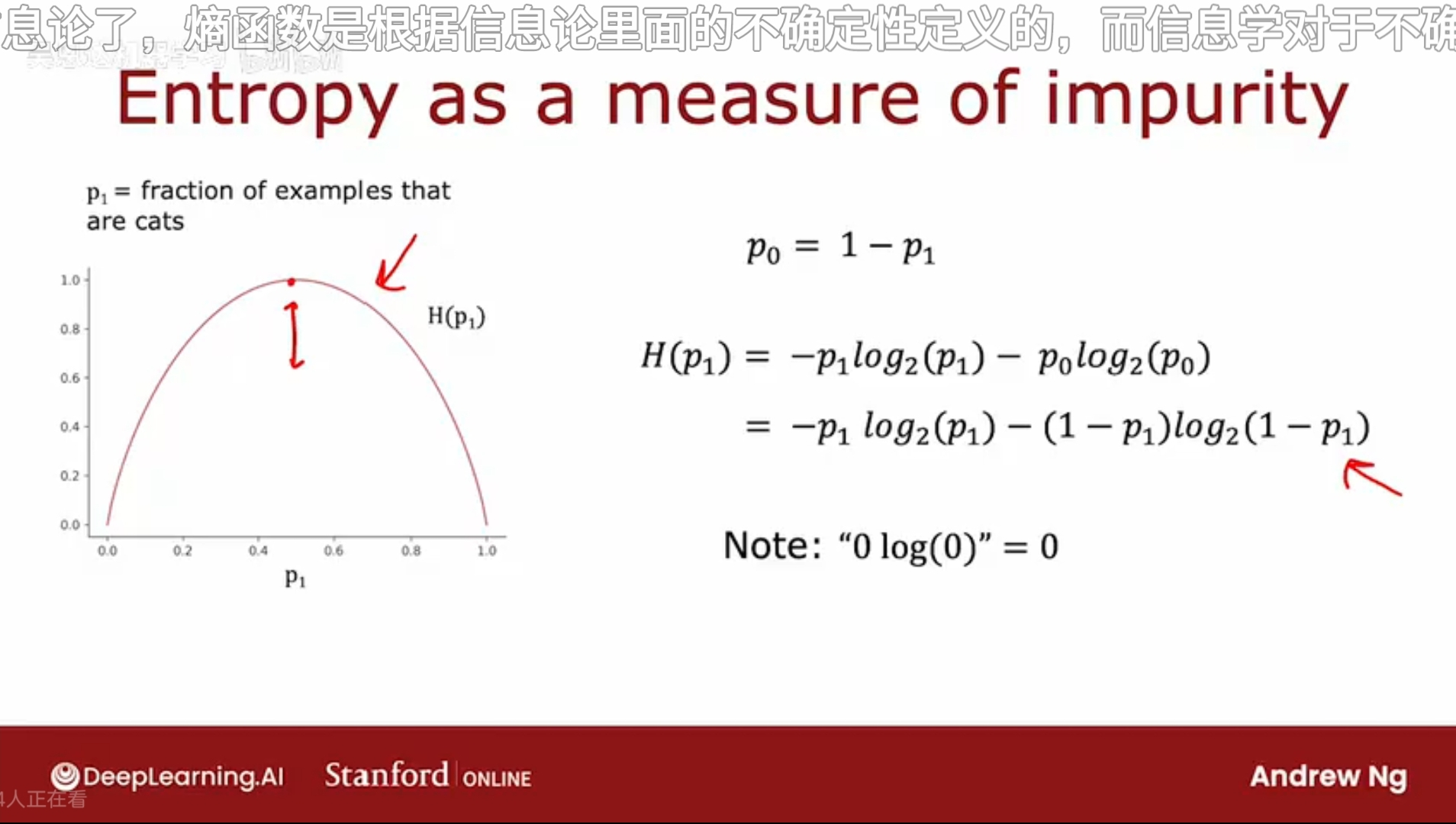
该熵函数的定义，看起来和损失函数的定义非常相似。存在数学依据，暂不讨论。

22.2 选择拆分信息增益

在构建决策树时，我们是如何选择特征来进行拆分呢？该特征的选择能够最大程度的减少熵，增加纯度；

在决策树学习中，熵的减少被称为信息增益，如何计算信息增益 information gain 呢？从而在决策树的每个节点上，选择某特征来进行拆分；

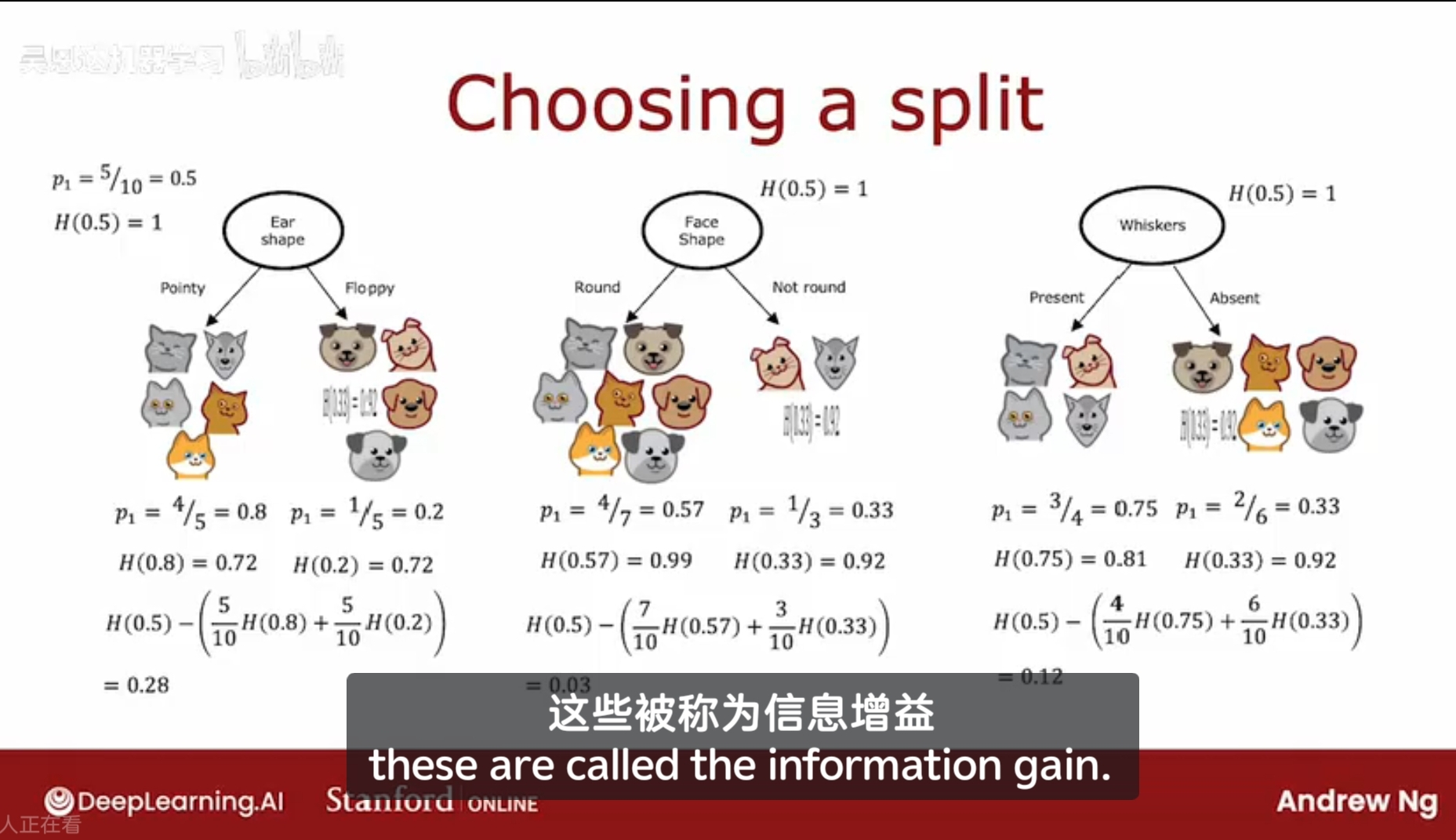
在某节点上，通过耳朵形状、脸形状、胡须来分类，可得到两组分类后的；

我们的目的是减少熵，增加纯度，但是对于数量级较少的组（比如分类后某组有两个，一个是猫，一个是狗，那它的熵是1，不纯度最高），

它所对应的熵的说服力较差，即它的熵值不太具备代表性，所以需要通过加权平均来计算熵，将两个熵值合为一个。

惯例上，使用和根节点对比起来的熵的差值，即熵的降低的数值，用来评估该特征是否是一个好的分类特征。使用根节点的熵值作为被减数；

寻找这个分类特征，即寻找熵值下降最快的方向。

事实证明，决定是否不再分类，其停止标准之一是看熵的减少程度；如果熵减少得太少，可能会决定，没有必要增加树的大小来取降低那么一点点熵，并且树越大，过拟合的风险越高。

如果熵低于某个阈值，也没必要继续分类下去了。

信息增益 Information Gain

w - 权重；

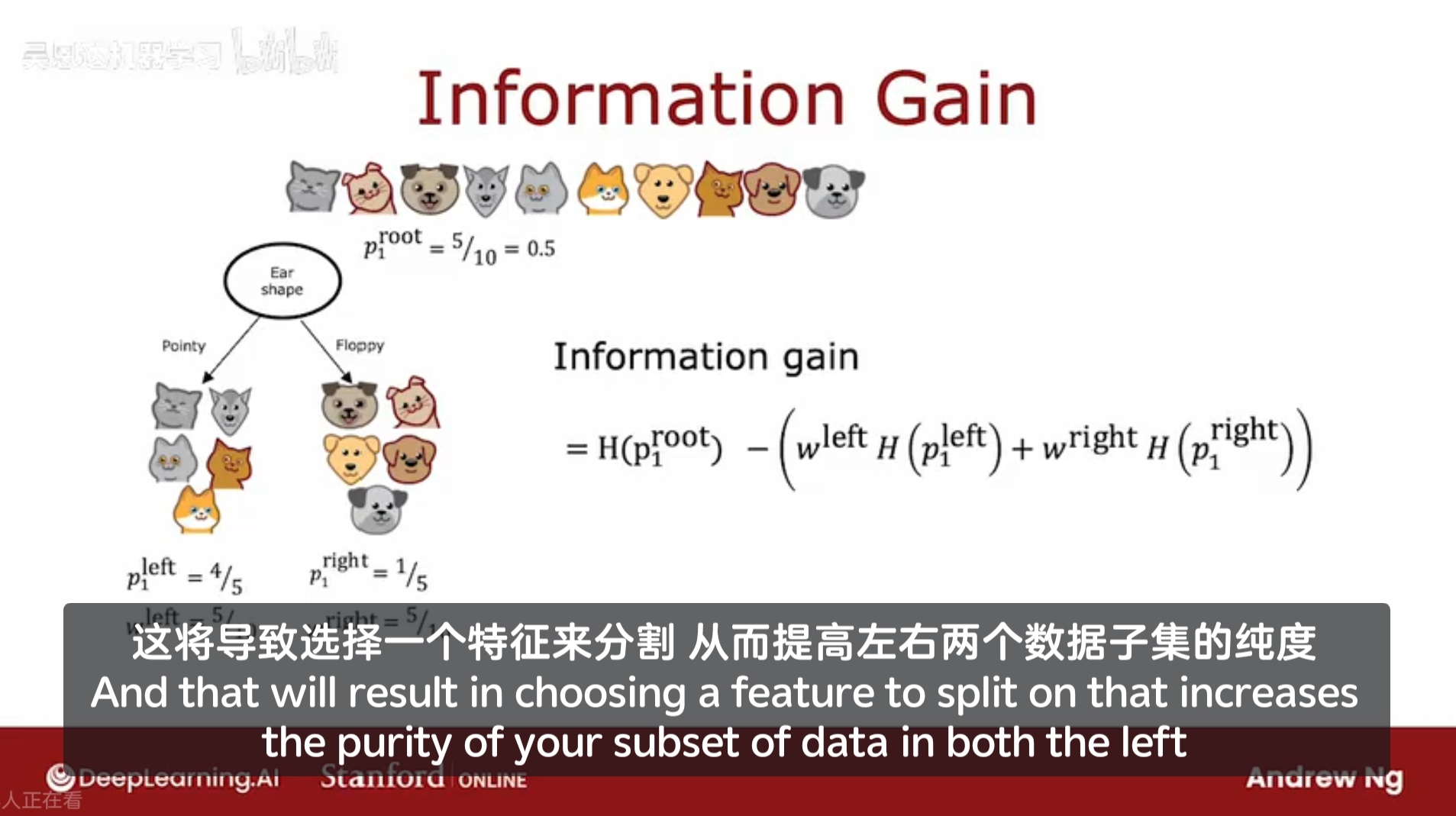
信息增益的定义：

根节点的熵值 - (左分支权重 * 左分支熵值 + 右分支权重 * 右分支熵值)

22.3 构建决策树的流程

信息增益标准，帮助决定在一个节点如何选择特征进行分类；

在决策树的多个地方使用该决策方法，来构建大型的决策树；

构建决策树的流程

1、在根节点开始，使用所有的样本集

2、对所有可能特征，计算信息增益，并选择熵减少最多的（即信息增益最多）那个特征；

3、根据选择的特征分组，创建左分支和右分支；

4、在树的左右分支上，重复进行特征选择和分类操作；直到达到停止标准：

当一个节点完全是一种单一类别；

再分裂节点会导致树超过设定的最大深度；

在分裂的信息增益少于一个阈值；

节点中的示例数低于阈值；

构建决策树的过程，类似于递归算法，当达到某个停止条件时，停止递归。

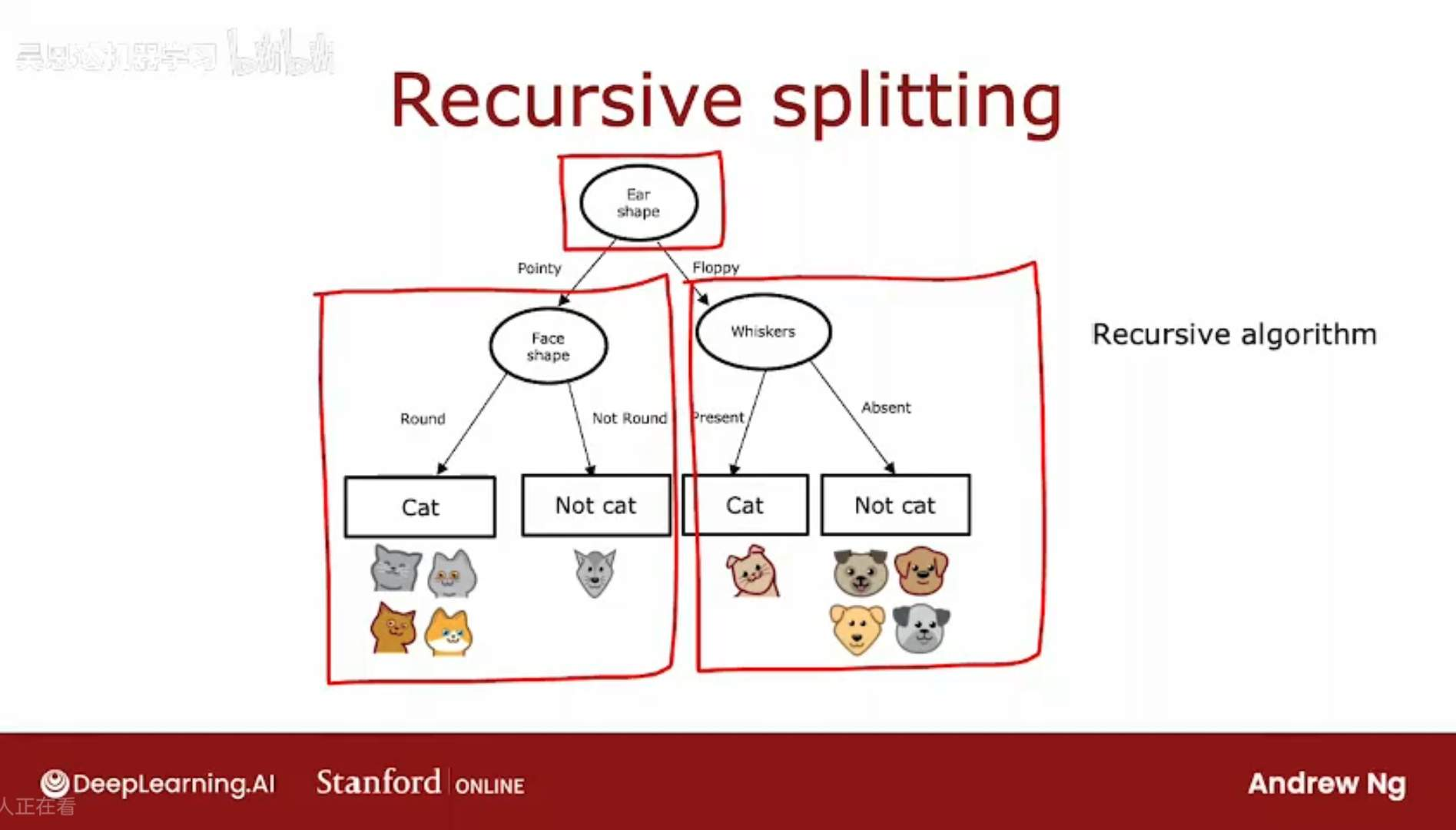
如何选择最大深度，

最大深度越大，你所构建的决策树就越大，有点像拟合高阶多项式，或训练更大的神经网络。让决策树学习更复杂的模型，为数据拟合一个非常复杂的函数，有很大的过拟合的风险。

理论上，可以使用交叉验证来选择参数，比如最大深度，尝试使用不同的深度，并选择在交叉验证集熵效果最好的。开源库有更好的方法来帮助选择参数。

在示例中，使用了两个类别，但有时会包含多个类别或离散值 discrete value 的特征，会存在多个类别。

22.4 使用分类特征的一种one-hot编码

对于一些分类特征，比如胡须的有无，用yes/no可以表示，但是比如脸型可能有矩形、三角形、圆型、椭圆形多种形状，这一种特征需要有好几个枚举值，才能表示。

比如耳朵形状，现在有Pointy尖的、Floppy耷拉的、Oval椭圆形，这意味着如果你使用耳朵形状对一批动物进行分类，你会得到三个子分支。

现在有一种新的解决特征标记的方法，即使用one-hot encoding，即将三种耳朵的形状重新分配为三种独立的特征：即，是否有尖耳朵、是否有耷拉的耳朵、是否有椭圆的耳朵

对于第一个动物，假设它有尖耳朵，则所对应的是否有尖耳朵的特征值为1，耷拉耳朵和椭圆耳朵的特征值为0；

If a categorical feature can take on k values, create k binary features (0 or 1 valued)

如果某种特征具有k个枚举值，则将该特征分为k个二元特征，每个特征的取值是0或1；

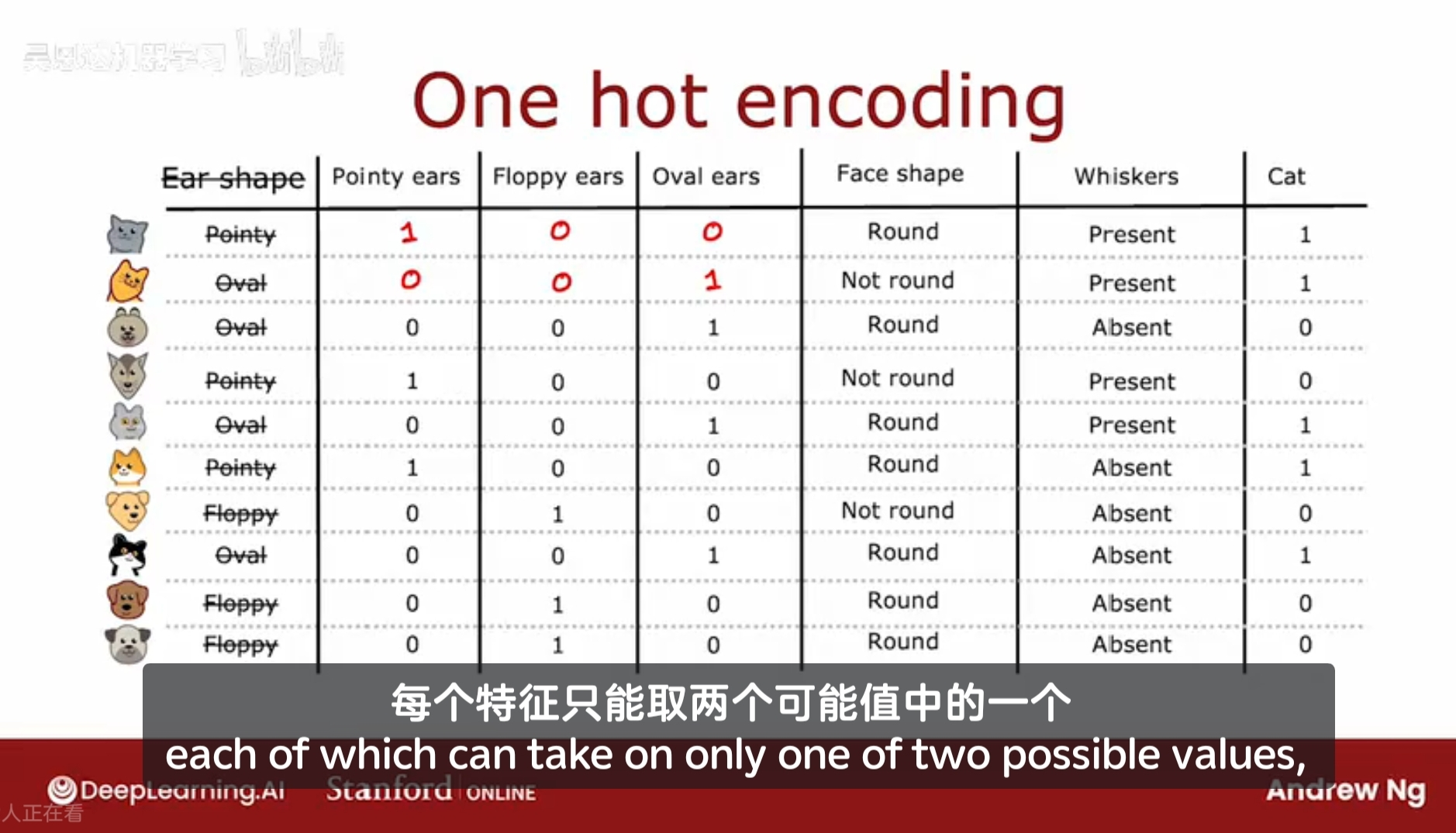
由某种特征衍生创建出的k个二元特征，这些k个二元特征中只有一个为1，其他都为0，所以这种特征构造方法称为 one-hot encoding。其中只有一个特征的取值为1，该特征称为 one-hot。

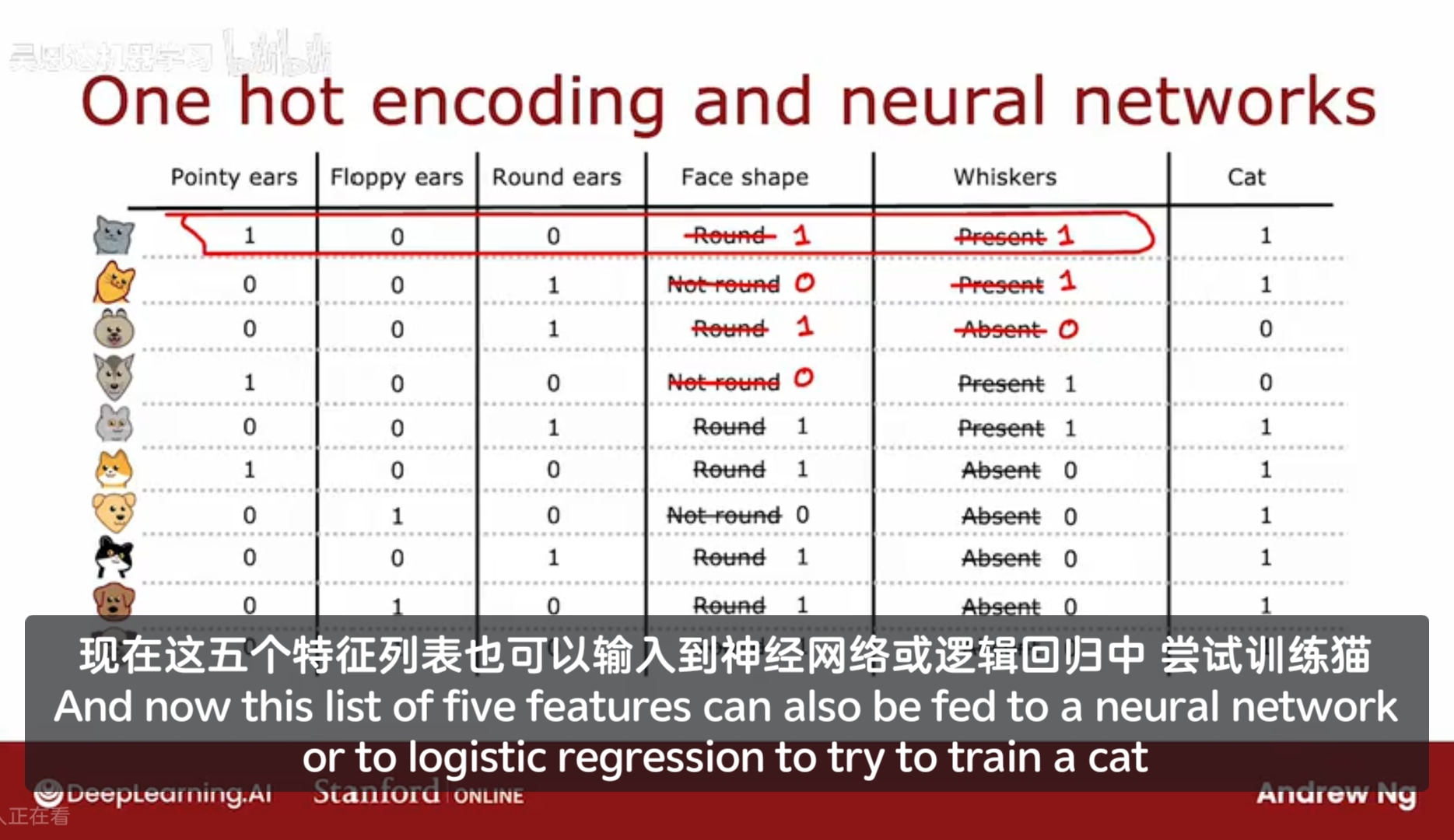
使用one-hot encodeings来编码类别特征的方法，也适用于训练神经网络（不止适用于决策树）。

通过将特征编码为0/1，来作为神经网络的输入。

通过one-hot encoding可以处理超过两个离散值的特征。

那如何处理一些可以取任意值的特征呢？而不是有限个离散值的特征，如何处理可连续取值的特征？

22.5 处理具有连续值的特征

在决策树中，如何处理那些可能取值为任意值的特征呢？

例子：在猫咪收养分类系统（区分猫和其他动物），增加一个特征：体重；

增加体重这个特征，也是为了能获得更多的信息增益，即，能够更好地将猫和狗区分开来的信息；（信息增益Information gain：熵的减少值，根节点的熵 - 加权平均后的子节点的熵）

熵函数H§：一个开口向下的曲线，峰值为1，轴线为0.5；

当考虑基于体重特征划分时，需要界定一个阈值，当小于等于该阈值时，认定为猫，否则认定为狗；

体重是一个连续值，需要考虑取若干不同的阈值，分别来计算它们的信息增益，从而选取信息增益最大的那个阈值。

实际上，所尝试的阈值不止三个，而是沿着x轴逐个尝试，一种惯例是根据体重（根据这个特征的值）对所有样本进行排序，取排序后的样本列表中所有值的中点（midpoints）作为阈值来考虑，即如有十个样本，那么取九个中点的值，作为阈值来测评。根据每个阈值来计算信息增益，最后选择得到信息增益最大的那个阈值。

小结：为了让决策树在每个节点处理连续值特征时能分割，考虑使用不同的值来分类，进行常规的信息增益计算，然后选择信息增益最大的那个阈值。

22.6 决策树泛化为回归算法

将决策树泛化为回归算法，以便能预测；

问题：如果一个动物它是尖尖耳朵，圆脸，那么它的预测的体重是？

决策树将基于训练样本中的权重平均值进行预测。

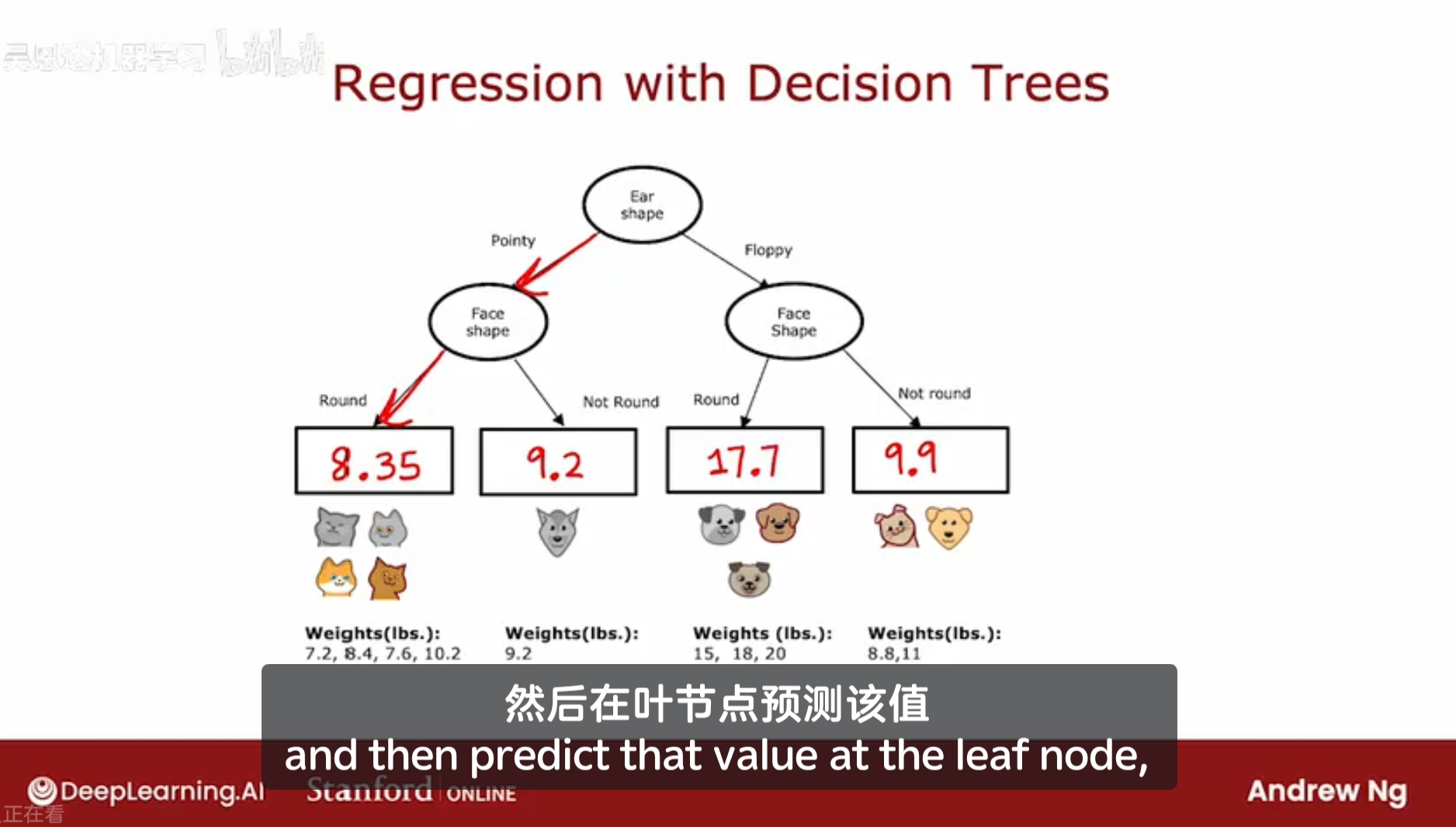
如果从头构建一颗决策树，如何选择特征，使用这个数据集来预测体重，如何选择特征以分类

这颗决策树的目的不是分类，而是预测体重（不用管猫或狗），即通过哪个特征分类所得到的两组，他们的体重值的方差最小，那么通过该特征所预测的体重就越好。

（具备哪种特征的动物，可能具备更大的体重/更小的体重/平均体重）

对于每个特征所分类的两组，计算它们的方差，及加权平均后的值。

类似于信息增益中，计算的是熵的减少值，这里也计算方差的减少值，所以需要计算根节点数值的方差值。

含义是，通过某特征的分类，该组体重值的变动/方差变得更加小，预测的也就更准确。

在回归树中，选择带来最大的方差减少的特征。

选择了耳朵作为分类特征后，再分别拿左右的五个样本，来继续构建决策树，选择新的特征来分组（选择那个能带来最大方差减少的特征），从而使得体重值的分布更加均匀，方差更小，递归地循环这个过程，直到达到了可以停止的标准。

比如方差小于某个阈值，比如回归树的深度达到最大深度，等。

22.7 使用多个决策树

使用单个决策树的缺点：它可能对数据中微小的变化高度敏感；

方案：构建多个决策树，决策树集群 tree ensemble，以达到更稳健的算法，

仅改变一个样本时，信息增益的最高的特征就会从耳朵变为胡须。

改变一个样本就能导致算法在根节点进行不同的分割，从而得到完全不同的树，这使得这个算法比较敏感，不稳健not robust。

如果不止训练一棵树，而是训练一堆不同的树，会得到更加精准的预测。

Tree ensemble 树集成

假设有三棵树，每颗都是一种合理的区分猫和非猫的方法。

如果有一个新样本来区分猫和非猫；

需要做的就是在这个新样本上运行这三棵树，并且让它们对最终预测投票，。

假设一个样本，它有尖尖耳朵，非圆脸，有胡须，在这三棵树上，分别预测得到的结果是：猫、非猫、猫；

实际上会让他们投票，投票结果为两个猫一个非猫，那么这个树集成的预测结果就是猫。

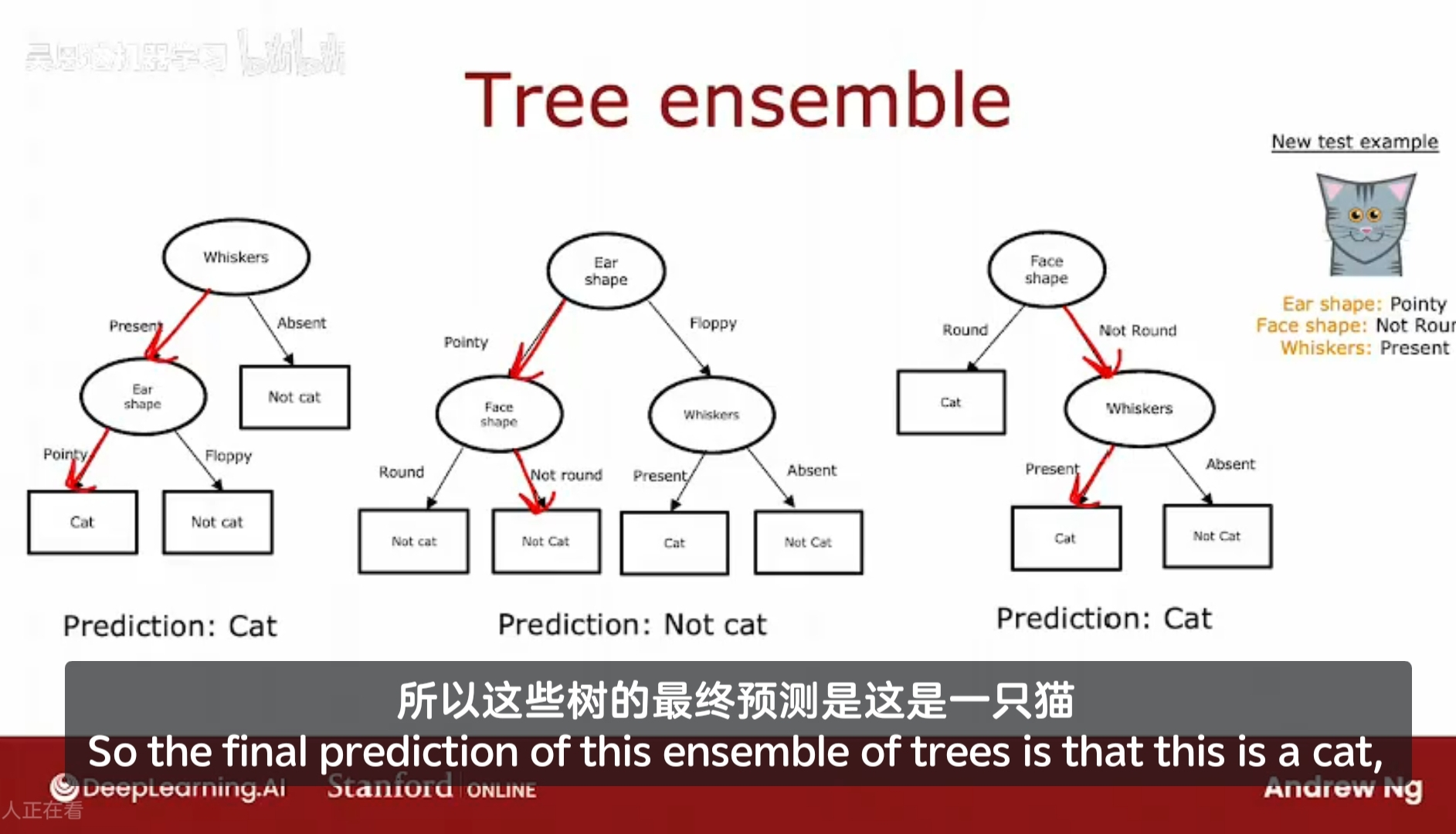
我们使用树集成的原因是它拥有大量的决策树，并且让他们投票，这使得整体算法对任何单颗树的影响变得不那么敏感。这使得整个算法更加健壮。

但是，如何得出所有这些树的不同结果的合理解释呢？对于同样的样本，但是每颗树的预测结果可能不同，如何让它们进行合理的投票？

一种统计学中的技术，有放回抽样，有助于构建树集成。

22.8 构建树集合-有放回抽样

四个颜色的tokens：红色、黄色、绿色、蓝色；

进行有放回的抽样；

多次重复这个有放回的抽样；

有放回抽样在构建树集合中的应用：

构建多个随机训练集，这些训练集和原始训练集略有不同。

原始训练集：五只猫 + 五只狗；

从训练集中随机取一只动物，记录特征（耳朵脸型胡须等），并放回

然后重复这个有放回抽样的过程，不断记录特征。

最后得到十个例子，其中有些是相同的。最后得到的这个训练集并不是原始训练集的全部，只是其中的一部分。

有放回的抽样过程，构造了一个新训练集，有些类似于原始训练集，但又不同。

这将是构建树集合的关键。

随机森林算法：一个强大的树集合算法，效果远好于使用单个决策树。

构建树样本：

一个大小为 m 的训练集；

b = 1 写为 B

使用有抽样放回方法创建一个大小为m的新训练集（可能存在重复样本）；

使用这个新训练集训练一个决策树；

重复执行第2、3步，得到一个新的决策树。

B为循环重复的次数，建议64-128,；

假如生成了100个决策树，在下一次的预测中，让这100个树都参与投票决策。

事实证明，设定更大的B，不会影响性能。但超过某个值后，收益会递减，当B远大于该数值时，实际效果不会有明显的提升。该数值大概在100左右。

这种树集成的具体实例有时也被称为袋装决策树，指的是将原始训练集放入虚拟袋中，以构建新训练集。

改良：修改这个算法，可以使其表现更好。这会将这个算法从袋装决策树 bagged decision tree 转变为 随机森林算法 the random forest algorithm。关键思想是，即使使用这种有放回的抽样程序，有时你最终总是在决策树的根节点使用相同的分裂，以及在根节点附近进行非常相似的分裂。（在当前示例的训练集中，根节点使用了不同的特征来分类，但实际对于其他很多数据集来说，在决策树的根节点几乎总是使用相同的特征来分类）。

对算法可以修改，可以进一步尝试在每个节点随机化特征选择，这些在节点处特征的更随机的选择，可能会导致所训练得到的树集合变得更加的不同（认为是学到了更多维度的特征？及其关联关系？因为原数据集放回抽样得到的新训练集总是相似的？）。这样，你会得到更加准确的预测。

通常的做法是，在每个节点选择特征进行分裂时，如果有n个特征可用，我们从中选择一个特征的随机子集（包含k个特征，k<n），并允许算法仅从这k个特征子集中选择，换句话说，你会选择k个特征作为允许选择的范围，从这k个特征中，选择信息增益最高的特征，作为分裂作用的特征。

当n很大时，比如几十个，几百个，k的典型选择是选择n的平方根。

这种做法既保证了公平性，也保证客观性，知识在树的数量的选择和特征的数量上，我们需要通过某种方法和公式进行权衡，在计算量和客观性中的 tradeoff。

随机森林算法，更多使用于具有大量特征的更大问题。

通过对这种算法的进一步修改，得到了随机森林算法，通常会工作的更好，比单个决策树要健壮 robust 得多。

为什么它更健壮？

放回抽样方法引起了算法探索了数据的许多小变化，用这些新训练集在训练不同的决策树时，这些变化是平均到数据上了，这意味着对训练集的任何小的进一步改动，都不太可能对随机森林算法整体的输出有较大的影响。因为它已经探索并平均了新训练集的许多微小变化。

1. 随机森林进一步降低模型方差，增强泛化能力
这是最根本的原因。

• 袋装法的作用：
  袋装法本身就是为了降低方差而设计的。通过对数据进行有放回抽样，并训练多个模型进行集成，可以平滑掉单棵决策树因对训练数据过于敏感而产生的高方差。但是， 如果基础模型（决策树）本身非常不稳定且高度相似，那么集成的效果会受限。

• 随机森林的改进：通过特征随机性，随机森林强制让每棵树变得更加“不同”。

分析：想象一下，如果所有树都在每个节点上审视所有特征，那么最有预测力的那几个特征总是会出现在树的顶部节点。这会导致所有树的结构非常相似，即树与树之间是高度相关的。虽然袋装法用了不同的数据子集，但如果数据有噪声，这些高度相关的树可能会“集体犯错”。

随机森林通过限制特征选择，刻意地让每棵树“学得差一点”、更片面一点。有的树可能因为没看到关键特征而被迫使用次要特征进行分裂。这样，每棵树都从不同的“视角”去看待数据。当这些多样化的、不完美的模型集成在一起时，它们犯的错误各不相同，通过“集体投票”可以互相纠正，从而得到更稳定、更准确的结果。这显著降低了模型整体的方差。

机器学习工程师在哪里露营？

在随机森林中…