基于python的机器学习(十)—— 评估算法(三)
目录
一、机器学习算法的比较
1.1 监督学习算法比较
1.2 深度学习算法比较
二、统计显著性检验
2.1 统计显著性检验的基本概念
2.1.1 P值
2.1.2 显著性水平(α)
2.2 常见的统计显著性检验方法
2.2.1 t检验
2.2.2 方差分析
2.2.3 卡方检验
2.3 现代替代方法与补充
三、模型性能对比方法
3.1 基准模型选择
3.1.1 经典模型
3.1.2 SOTA 模型
3.2 可视化对比
3.2.1 学习曲线
3.2.2 混淆矩阵
3.2.3 误差分布分析
四、过拟合与欠拟合检测
4.1 过拟合检测方法
4.2 检测欠拟合的方法
4.3 绘制学习曲线
一、机器学习算法的比较
1.1 监督学习算法比较
五种广泛使用的监督学习算法的简要描述:
-
线性回归(Linear Regression):用于回归任务,模型假设输出与输入特征呈线性关系。
-
逻辑回归(Logistic Regression):用于分类任务(尤其是二分类),通过Sigmoid函数将线性组合映射到概率。
-
支持向量机(SVM):主要用于分类,也可用于回归。核心思想是找到最大化类别间隔的超平面。对于非线性问题,使用核技巧(如高斯核)。
-
决策树(Decision Tree):用于分类或回归,通过树状结构递归分割数据。基于指标如信息增益或基尼指数选择分裂点。
-
随机森林(Random Forest):集成方法,由多个决策树组成。通过投票(分类)或平均(回归)提高准确性和鲁棒性。

| 算法 | 复杂度 | 训练速度 | 预测速度 | 准确度 | 过拟合风险 | 可解释性 | 适用场景 |
|---|---|---|---|---|---|---|---|
| 线性回归 | 低 | 快 | 快 | 中 | 低 | 高 | 简单线性关系、特征少的数据 |
| 逻辑回归 | 低 | 快 | 快 | 中 | 低 | 高 | 二分类、概率输出需求 |
| SVM | 中高 | 慢 | 中 | 高 | 中 | 中低 | 高维数据、小数据集、非线性问题(用核时) |
| 决策树 | 低 | 快 | 快 | 中 | 高 | 高 | 可解释性优先、类别特征多 |
| 随机森林 | 中 | 中 | 中 | 高 | 低 | 中低 | 高准确性需求、大数据集、特征多 |
| 算法 | 优点 | 缺点 |
|---|---|---|
| 线性回归 | 简单、高效、可解释性强;计算开销小 | 假设线性关系,对非线性数据表现差;易受异常值影响 |
| 逻辑回归 | 输出概率值,易于阈值调整;训练快速 | 仅适用于线性可分问题;对多重共线性敏感 |
| SVM | 高维空间表现好,通过核处理非线性;泛化能力强 | 训练慢(尤其大数据);调参复杂(如核函数选择);黑箱性强 |
| 决策树 | 直观易解释;处理类别特征和缺失值灵活 | 易过拟合;不稳定(小数据变化导致树结构大变 |
| 随机森林 | 准确性高,抗过拟合;处理高维数据好 | 训练较慢;可解释性低;预测时计算开销 |
1.2 深度学习算法比较

| 算法 | 复杂度 | 训练速度 | 预测速度 | 准确度 | 过拟合风险 | 可解释性 | 适用场景 |
|---|---|---|---|---|---|---|---|
| DNN(深度神经网络) | 极高 | 慢 | 中 | 极高 | 高 | 极低 | 大规模数据、复杂非线性关系 |
| CNN(卷积神经网络) | 高 | 慢 | 中 | 高-极高 | 中 | 低 | 图像/视频处理、空间特征提取 |
| RNN/LSTM | 高 | 极慢 | 慢 | 高 | 中高 | 低 | 时序数据、自然语言处理 |
| Transformer | 极高 | 极慢 | 慢 | 极高 | 中 | 极低 | 长序列建模、多模态数据 |
| GAN | 极高 | 极慢 | 中 | 高 | 高 | 极低 | 生成任务、数据增强 |
| 算法 | 优点 | 缺点 |
|---|---|---|
| 神经网络 (DNN) | 自动提取特征,无需人工干预;适应复杂非线性关系;可扩展性强 | 需要大量数据;训练时间长;计算资源消耗大;黑箱性强 |
| 卷积神经网络 (CNN) | 擅长处理图像/空间数据;局部感知减少参数量;权值共享提升效率 | 对非网格数据(如文本)效果有限;超参数调优复杂 |
| 循环神经网络 (RNN) | 处理序列数据(时间序列、文本);记忆历史信息 | 梯度消失/爆炸问题;长序列性能下降;训练速度慢 |
| 长短期记忆网络 (LSTM) | 解决RNN的长期依赖问题;记忆单元设计灵活 | 参数量大;计算成本高;仍可能受梯度问题影响 |
| 生成对抗网络 (GAN) | 生成高质量数据(图像、音频);无监督学习潜力大 | 训练不稳定(模式崩溃);难以评估生成质量;调参难度高 |
| Transformer | 并行计算效率高;注意力机制捕捉长距离依赖;NLP领域表现卓越 | 需要大量训练数据;自注意力计算复杂度高;可解释性差 |
二、统计显著性检验
2.1 统计显著性检验的基本概念
统计显著性检验是一种用于判断样本数据是否支持或拒绝某个假设的统计方法。其核心是通过计算概率(p值)来评估观察到的差异或效应是否由随机误差引起,还是反映了真实的总体特征。
- 零假设(H₀):默认假设,通常表示“无效应”或“无差异”。例如,两组均值相等(H₀: μ₁ = μ₂)。
- 备择假设(H₁):与研究目标一致的对立假设,可能为“有效应”或“有差异”(如 H₁: μ₁ ≠ μ₂ 或 μ₁ > μ₂)。
2.1.1 P值
p值表示在零假设成立的前提下,观察到当前数据(或更极端数据)的概率。若p值小于预设的显著性水平(如 0.05),则拒绝零假设。
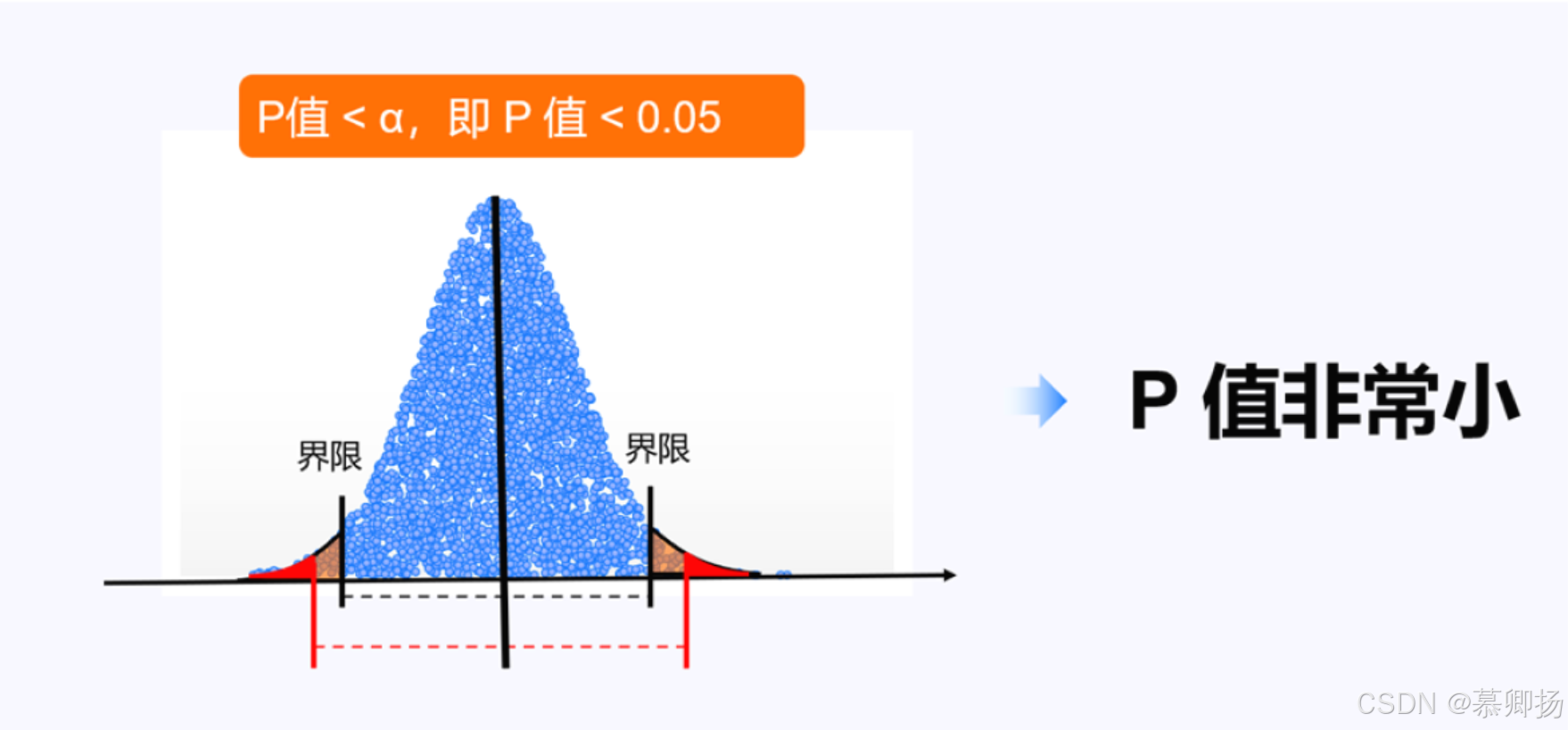
2.1.2 显著性水平(α)
预先设定的阈值(α)(通常为 0.05、0.01),用于定义统计显著性的标准。若p ≤ α,认为结果具有统计显著性。
2.2 常见的统计显著性检验方法
2.2.1 t检验
t检验用于比较两组数据的均值是否存在显著差异,适用于样本量较小(通常小于30)且总体方差未知的情况。分为独立样本t检验(两组数据独立)和配对样本t检验(两组数据相关)。
代码示例:
import numpy as np
from scipy import stats# 生成两组随机数据
group1 = np.random.normal(loc=50, scale=10, size=30)
group2 = np.random.normal(loc=55, scale=10, size=30)# 执行独立样本t检验
t_stat, p_value = stats.ttest_ind(group1, group2)
print(f"t-statistic: {t_stat:.4f}, p-value: {p_value:.4f}")2.2.2 方差分析
方差分析用于比较三组及以上数据的均值差异,通过分析组间方差和组内方差的比值判断显著性。分为单因素ANOVA(一个自变量)和多因素ANOVA(多个自变量)。
代码示例:
import numpy as np
from scipy.stats import f_oneway# 生成三组随机数据
group1 = np.random.normal(loc=50, scale=10, size=30)
group2 = np.random.normal(loc=55, scale=10, size=30)
group3 = np.random.normal(loc=60, scale=10, size=30)# 执行ANOVA检验
f_stat, p_value = f_oneway(group1, group2, group3)
print(f"F-statistic: {f_stat:.4f}, p-value: {p_value:.4f}")2.2.3 卡方检验
卡方检验用于分析分类变量之间的关联性或拟合优度,包括卡方独立性检验(检验两个分类变量是否独立)和卡方拟合优度检验(检验观测分布与理论分布是否一致)。
代码示例:
import numpy as np
from scipy.stats import chisquare# 观察值和期望值
observed = [30, 20, 25, 25]
expected = [25, 25, 25, 25]# 执行卡方检验
chi_stat, p_value = chisquare(observed, f_exp=expected)
print(f"Chi-square statistic: {chi_stat:.4f}, p-value: {p_value:.4f}")2.3 现代替代方法与补充
传统的统计显著性检验(如p值检验)存在局限性,现代统计学发展出多种替代方法:
- 贝叶斯方法:通过计算贝叶斯因子(Bayes Factor)比较假设的相对支持程度,避免仅依赖p值。
- 效应量估计:直接报告效应量(如Cohen's d、OR值)及其置信区间,避免二元显著性判断。
为弥补传统检验的不足,可结合以下方法提升分析深度:
- 自助法(Bootstrap):通过重复抽样构建统计量的经验分布,计算稳健的置信区间。适用于非正态数据或复杂统计量。
- 预注册与多重检验校正:预先公开分析计划减少p-hacking风险,对多重比较使用FDR(错误发现率)或Bonferroni校正。
- 可视化分析:绘制森林图、小提琴图或累积效应图直观展示数据分布与不确定性。
三、模型性能对比方法
3.1 基准模型选择
选择基准模型时,需结合任务特性:
- 若任务偏向传统数据(如表格数据),经典模型可能更合适。
- 若任务涉及高维数据(如图像、文本),优先选择SOTA模型。
3.1.1 经典模型
经典模型通常指经过时间验证、广泛使用的基准模型,如线性回归、决策树、支持向量机(SVM)等。这些模型结构简单,计算效率高,适合作为性能对比的基线。经典模型的优势在于可解释性强,便于理解模型的局限性。
3.1.2 SOTA 模型
SOTA(State-of-the-Art)模型指当前领域内性能最优的模型,如Transformer、EfficientNet等。选择SOTA模型作为对比基准,可以验证新模型是否具备竞争力。SOTA模型通常复杂度较高,需考虑计算资源与训练时间。
3.2 可视化对比
3.2.1 学习曲线
学习曲线反映模型在训练集和验证集上的性能随训练样本或迭代次数的变化趋势。理想情况下,训练误差和验证误差应逐渐收敛。若训练误差低但验证误差高,可能存在过拟合;若两者均高,可能存在欠拟合。
3.2.2 混淆矩阵
混淆矩阵用于分类任务,直观展示模型在不同类别上的预测情况。通过矩阵的行(真实类别)和列(预测类别),可计算精确率、召回率等指标。例如:
| 预测正类 | 预测负类 | |
|---|---|---|
| 真实正类 | TP | FN |
| 真实负类 | FP | TN |
3.2.3 误差分布分析
误差分布通过直方图或箱线图展示模型预测误差的统计特性。例如:
- 回归任务中,观察误差是否服从均值为零的正态分布。
- 分类任务中,分析错误样本的分布规律(如特定类别易混淆)。
四、过拟合与欠拟合检测
4.1 过拟合检测方法
- 训练集与测试集表现差异:比较模型在训练集和测试集上的性能指标(如准确率、损失值)。若训练集表现远优于测试集,可能存在过拟合。
- 学习曲线分析:绘制训练集和验证集的损失/准确率随训练样本数或迭代次数的变化曲线。若验证集曲线停滞或上升,而训练集曲线持续下降,可能存在过拟合。
- 交叉验证:通过K折交叉验证观察模型在不同数据子集上的表现波动。若验证集性能差异大且普遍低于训练集,可能过拟合。
- 正则化效果验证:引入L1/L2正则化或Dropout后,若测试集性能提升,说明原模型可能存在过拟合。
4.2 检测欠拟合的方法
- 训练集表现低下:若模型在训练集上的性能未达到预期(如准确率过低),可能存在欠拟合。
- 学习曲线平坦:训练集和验证集的损失/准确率曲线均收敛于较低水平,可能因模型复杂度不足或特征缺失导致欠拟合。
- 特征重要性分析:检查模型是否忽略了关键特征。若添加有效特征后性能显著提升,原模型可能欠拟合。
- 模型复杂度测试:尝试增加模型复杂度(如更多层、更高次项)。若性能提升,原模型可能欠拟合。
4.3 绘制学习曲线
from sklearn.model_selection import learning_curve
import matplotlib.pyplot as pltdef plot_learning_curve(estimator, X, y):train_sizes, train_scores, test_scores = learning_curve(estimator, X, y, cv=5, scoring='accuracy')plt.plot(train_sizes, train_scores.mean(axis=1), label='Training score')plt.plot(train_sizes, test_scores.mean(axis=1), label='Validation score')plt.xlabel('Training examples')plt.ylabel('Accuracy')plt.legend()plt.show()