【Python刷力扣hot100】11. Container With Most Water

问题

给定一个长度为n的整数数组height。绘制n条垂直线，其中第i条线的两个端点分别为(i, 0)和(i, height [i])。
找到两条垂直线，使其与 x 轴共同构成一个容器，且该容器能容纳最多的水。
返回容器可容纳的最大水量。

注：容器不可倾斜

例1：

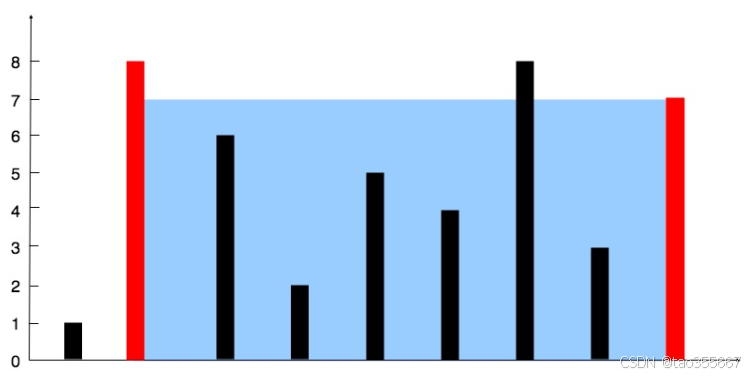
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
解释: 上述垂直线由数组 [1,8,6,2,5,4,8,3,7] 表示。在该情况下，容器能够容纳的最大水量（蓝色区域部分）为 49。

例2：

Input: height = [1,1]
Output: 1

约束:

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

解1：常规遍历

两根线盛水量就是 他们x轴坐标之差*它们之间较短的线。可以遍历数组，共尝试$\frac{n(n-1)}{2}$次，找到最大的盛水量。

时间复杂度$O(n^2)$：嵌套遍历数组，共尝试$\frac{n(n-1)}{2}$次。
空间复杂度$O(1)$：需要的空间大小是固定的，使用几个变量即可。

class Solution:def maxArea(self, height: List[int]) -> int:ans=0for i in range(len(height)):for j in range(i+1,len(height)):ans=max(ans,(j-i)*min(height[i],height[j]))return ans

方法没问题，但是时间花费太多，会超时

解2：双指针

1. 定义左指针l和右指针r，l初始指向数组开头(0)，r初始指向数组末尾。
2. 计算面积area，之后将height[l]和height[r]中较短的抛弃，也就是向右移动l或向左移动r。不断重复步骤2，直到l和r相遇，也就是数组height被遍历了一遍

思考：

• 抛弃短板，也就是跳过一部分情况，以缩短时间。通过遍历一次数组得到答案。
• 为什么要抛弃短板？ 如果我们抛弃长板，那么如果下一个板还是长板，水的面积显然会更小，因为x轴长度缩短了，如果下一个板子比现在的短板还短，那显然水的面积还是会小。所以抛弃长板是没有收益的。抛弃短板，情况才有可能变得更好。
• 抛弃短板时有没有可能跳过最优的情况？ 不会，因为每次计算的情况都是当前短板的“最优情况”，上面已经说过，当短板确定时，长板再怎么变化，都没办法让情况变得更好，所以每次计算时，都是当前短板存在时的最优情况。所以我们在移动短板时，会得到所有短板的最优情况（一堆极大值），我们需要的最终结果也是一个长板的一个短板组成，所以最终也会得到最优情况（一个最大值）。相当于在一堆极大值中间找最大值。

公式推导可参考官方题解

class Solution:def maxArea(self, height: List[int]) -> int:ans=0l=0;r=len(height)-1while l<r:area=(r-l)*min(height[l],height[r])ans=max(ans,area)if(height[l]<height[r]):l+=1else:r-=1return ans

参考

https://leetcode.cn/problems/container-with-most-water