PyTorch深度学习(入门笔记)
本文参考:
《PyTorch深度学习实践》完结合集
特别感谢 刘二大人 给我的帮助
Backward
反向传播
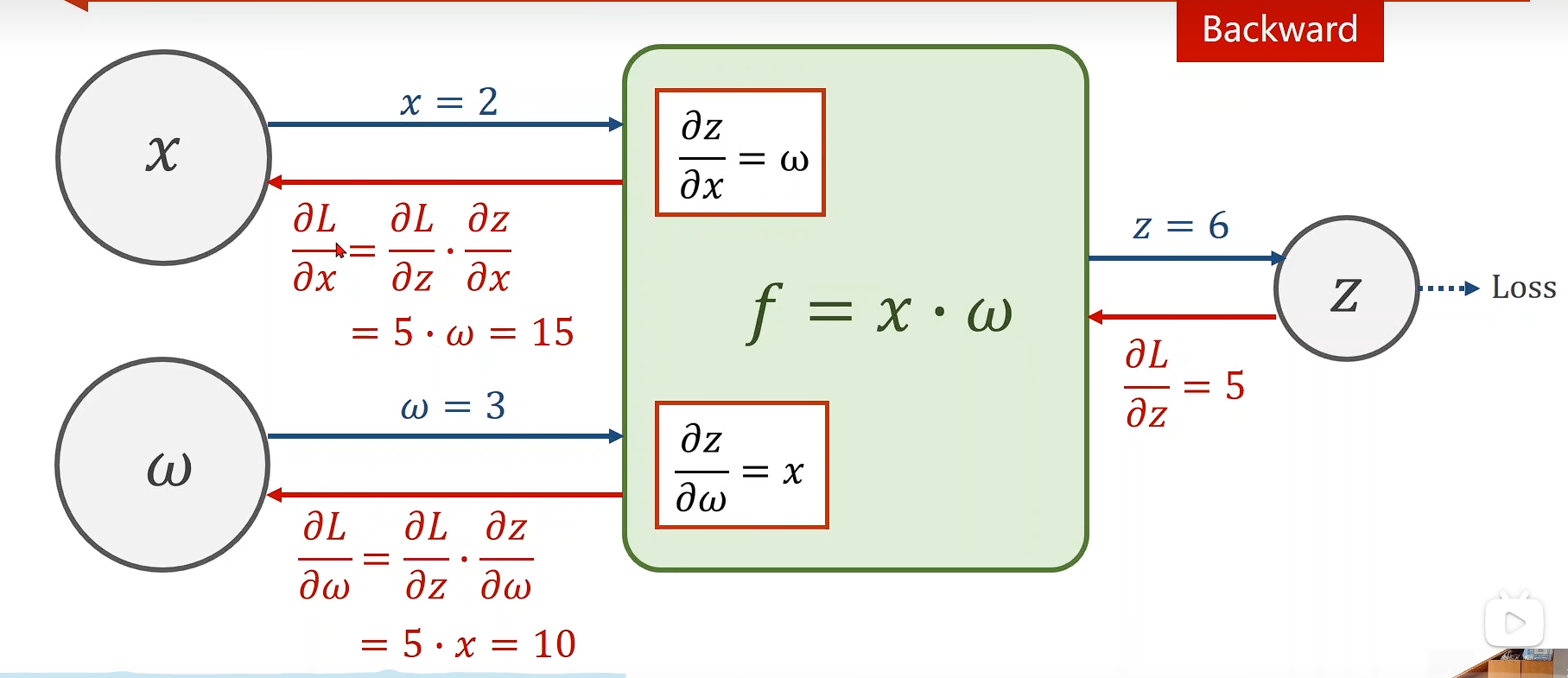 前馈 & 反馈在跟新的时候我们要的就是梯度
前馈 & 反馈在跟新的时候我们要的就是梯度
绿色的是模块,我们只需要先把模块搞定。
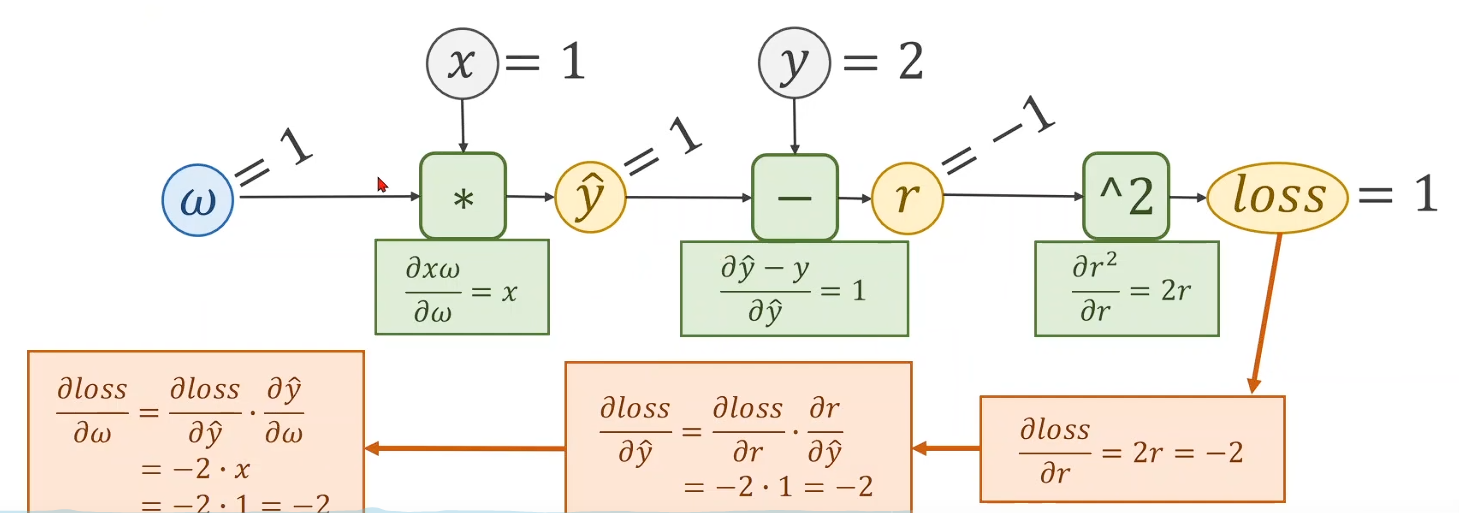
Eg
y^=x×w\widehat{y}=x \times wy=x×w
pytorch核心数据结构
tensor
简单来说,Tensor(张量)是一个多维数组,它是 PyTorch 中最基本的数据结构,所有模型的输入、输出和参数都是用 Tensor 来表示的。
特性:
-
多维性:Tensor 可以表示各种维度的数据。
-
加速计算:Tensor 可以被方便地移动到 GPU(或其它硬件加速器,如 MPS)上,利用其并行计算能力极大地加速运算。
非常重要的属性:
- grad:存储的是梯度(Gradient)。注意这个也是Tensor
- 关键特性:
- 初始状态下,
.grad是None。 - 只有在调用
.backward()方法后,它才会被填充为梯度 Tensor。 - 它也不要求梯度(
requires_grad=False),因为梯度本身通常是计算的终点,不需要再对它求导。
- 初始状态下,
- 关键特性:
- data**:是 Tensor 的"数据"部分,它不包含计算历史。**注意这个也是Tensor
- 关键特性:对
.data的操作不会被自动求导系统(Autograd)跟踪。它的requires_grad属性为False。
- 关键特性:对
怎么使用?
首先 import torch
Eg: y^=w×x\widehat{y} = w \times xy=w×x
设置权重
w = torch.Tensor([1.0])
ps:需要用[]括起来
w.requires_grad = true
意思是它是需要计算梯度的,默认是不计算梯度的。
import torch
# y = wx
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
k = 0.01 #learning rate
w = torch.Tensor([1.0])
w.requires_grad = True
def forward(x):return w * x #自动把 x 变成Tensor再参加计算def loss(x, y):return (y - forward(x)) ** 2# Core operationfor epoch in range(1000):for x, y in zip(x_data, y_data):l = loss(x, y)l.backward() #backwardw.data = w.data - k * w.grad.dataw.grad.data.zero_() #w.grad清零,即释放,用于下次计算print('progress:', epoch, l.item())print("predict (after training):", 4, forward(4).item())用pytorch实现线性回归
- 先构建数据集
- 设计模型 (计算y^\widehat{y}y)
- 构造损失函数 & 优化器 (using PyTorch API)
- 训练周期,前馈 反馈 更新
构建数据集
使用 mini-batch 的风格
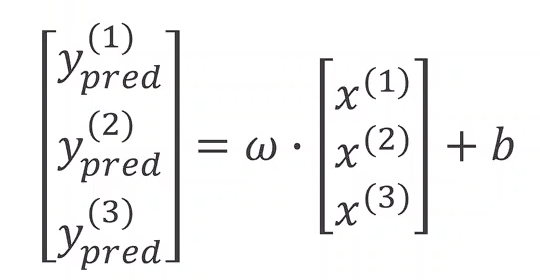
y^=w⋅x+by^1=w⋅x1+by^2=w⋅x2+by^3=w⋅x3+b\begin{gathered}\hat{y}=w \cdot x+b \\ \hat{y}_1=w \cdot x_1+b \\ \hat{y}_2=w \cdot x_2+b \\ \hat{y}_3=w \cdot x_3+b\end{gathered}y^=w⋅x+by^1=w⋅x1+by^2=w⋅x2+by^3=w⋅x3+b
[Loss 1Loss 2Loss 3]=([y^1y^2y^3]−[y1y2y3])23×1\left[\begin{array}{l}\text { Loss } _1 \\ \text { Loss } _2 \\ \text { Loss } _3\end{array}\right]=\underset{3 \times 1}{\left(\left[\begin{array}{l}\hat{y}_1 \\ \hat{y}_2 \\ \hat{y}_3\end{array}\right]-\left[\begin{array}{l}y_1 \\ y_2 \\ y_3\end{array}\right]\right) ^ 2} Loss 1 Loss 2 Loss 3=3×1y^1y^2y^3−y1y2y32
import torch
x_data = torch.tensor([[1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0]])
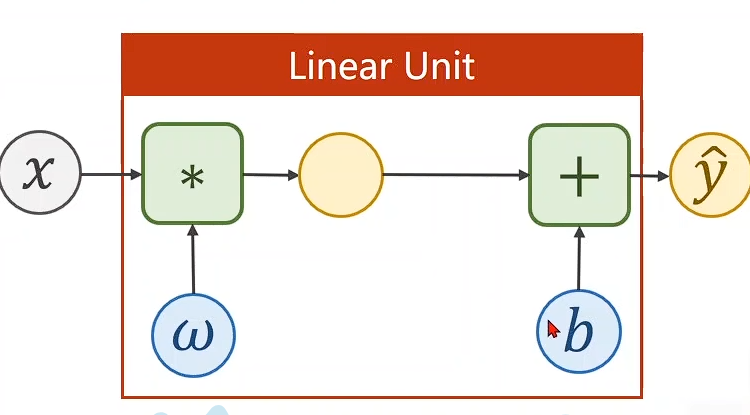
设计模型
把模型定义成一个类
class LinearModel(torch.nn.Module):def __init__(self):super(LinearModel, self).__init__() #构造函数 这一步是必须要有的self.linear = torch.nn.Linear(1, 1) #torch.nn.Linear一个类,(1, 1)构造对象def forward(self, x): #必须实现 前馈y_pred = self.linear(x)return y_predmodel = LinearModel()
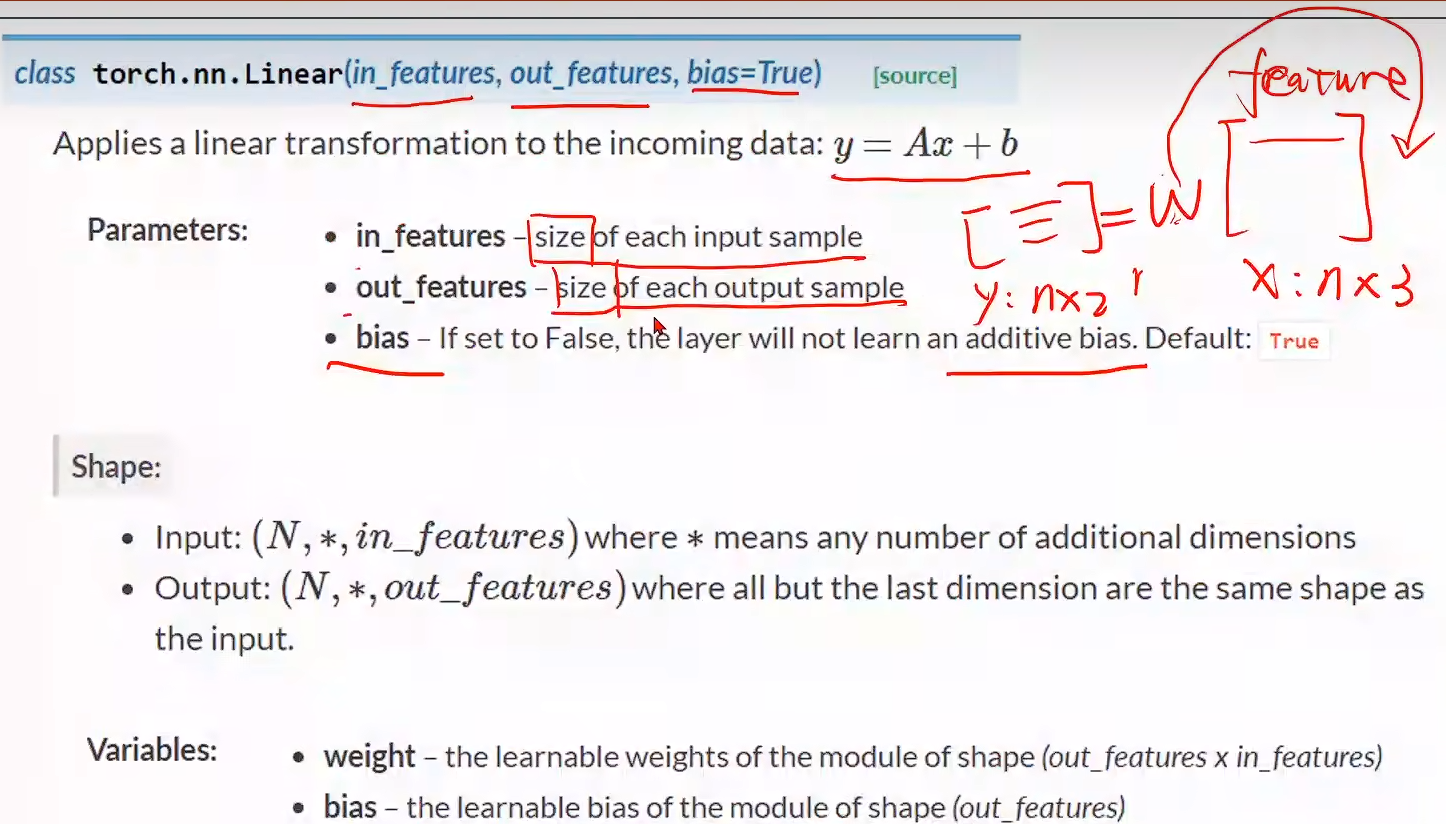
构造损失函数 & 优化器
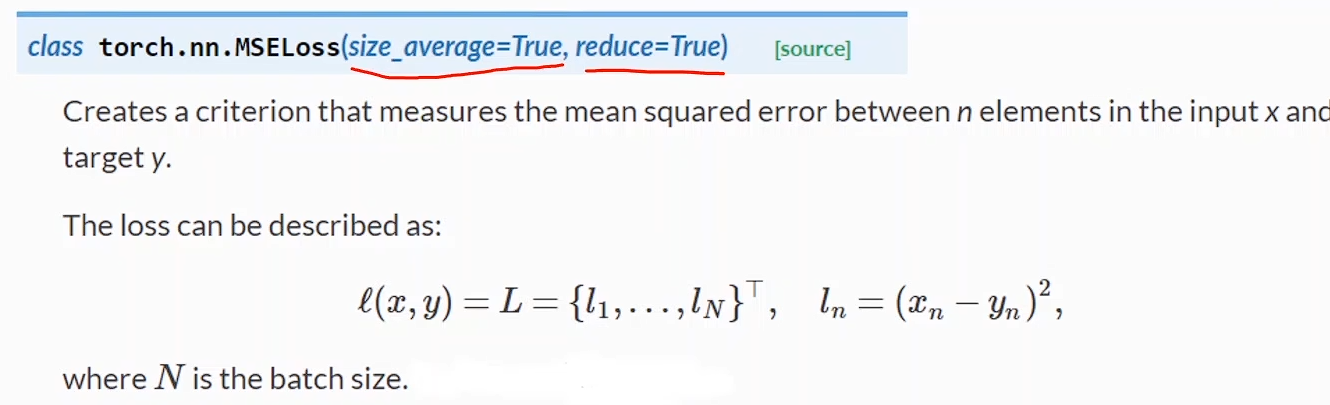
criterion = torch.nn.MSELoss(size_average=True)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)
MSELoss 也是继承 nn.Module
之后使用 criterion(y^,y\widehat{y}, yy,y) 就可以把损失算出来
model.parameters() 告诉优化器哪些参数需要进行随机梯度下降
lr = 0.01 学习率

训练的过程
for epoch in range(10000):y_pred = model(x_data) #算出 y_hatloss = criterion(y_pred, y_data) #算出损失print(epoch, loss) #loss是一个对象,打印的时候会自动调用__str__(),所以不会产生计算图,是安全的optimizer.zero_grad() #把所以权重的梯度都归0loss.backward() #反向传播optimizer.step() #更新 Update
总结:
-
计算 y^\widehat{y}y
-
loss
1 & 2 forward
梯度归零
-
backward
-
Update
逻辑蒂斯回归
torchvison


目录、训练集还是测试集、是否需要下载(第一次运行或者目录没有)
The database of handwritten digits
-
Training set: 60,000 examples,
-
Test set: 10,000 examples.
-
Classes: 10


-
Training set: 50,000 examples
-
Test set: 10,000 examples.
-
Classes: 10
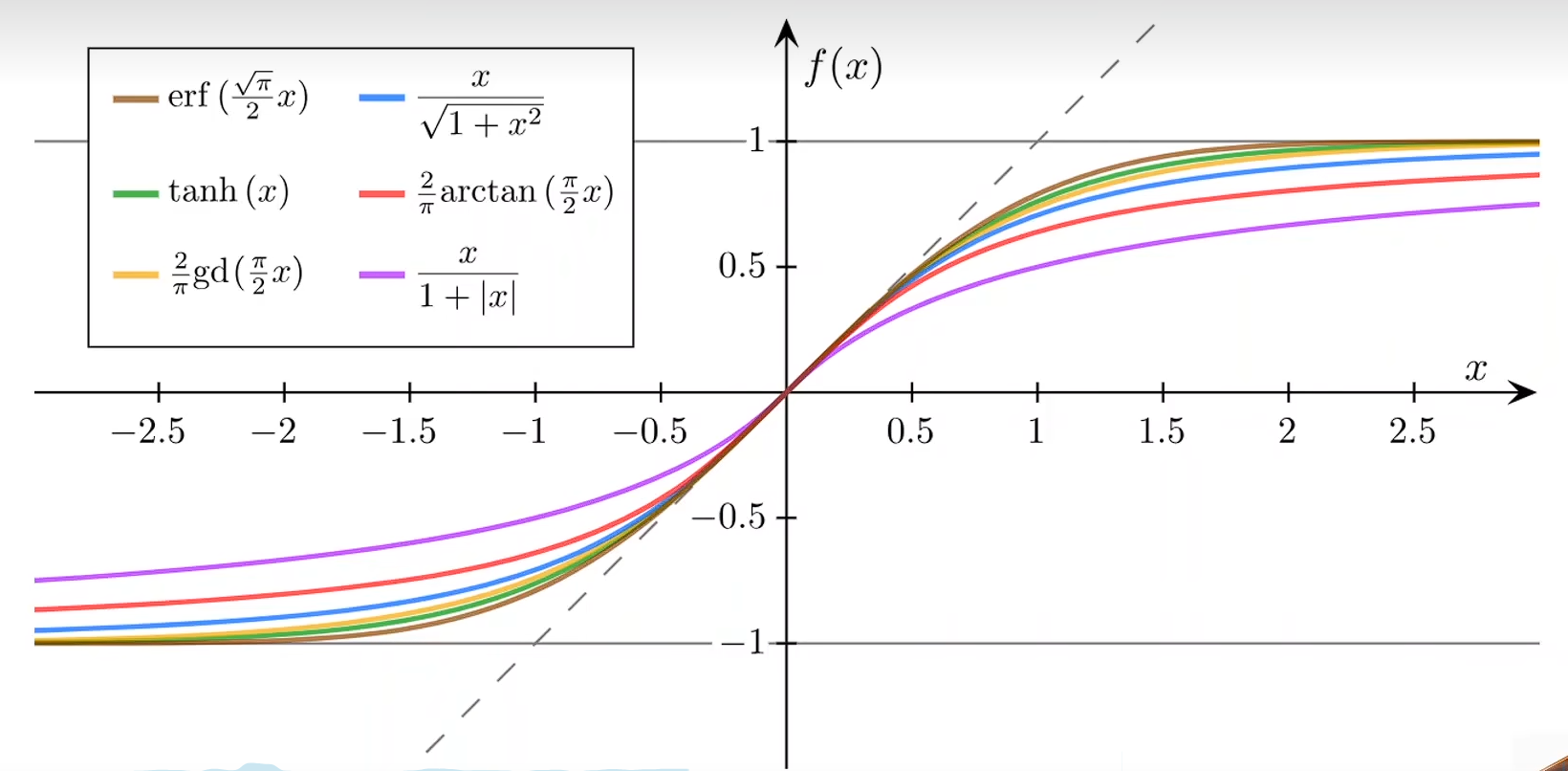
Logistic Function
sigmoid
σ(x)=11+e−x\sigma(x) = \frac{1}{1+e^{-x}}σ(x)=1+e−x1
把 y^\widehat{y}y 处理到 [0, 1] 这个区间
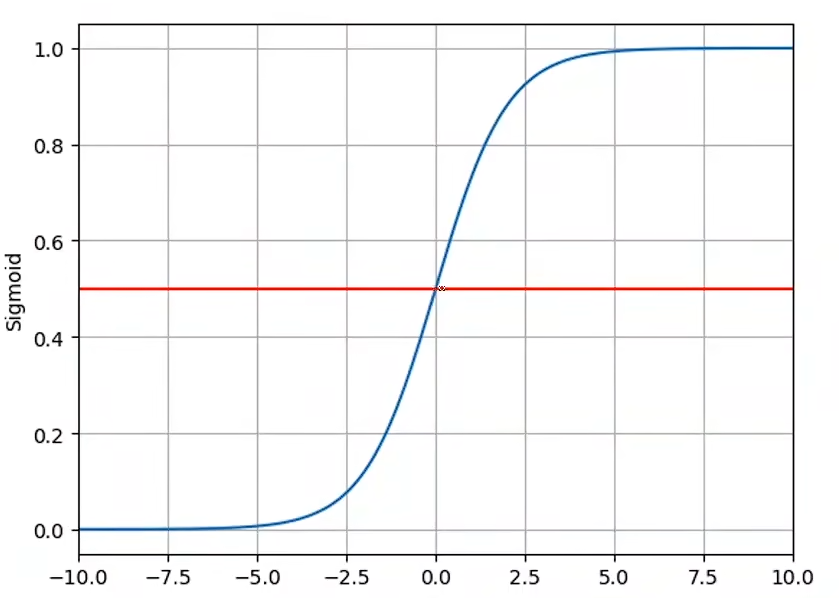
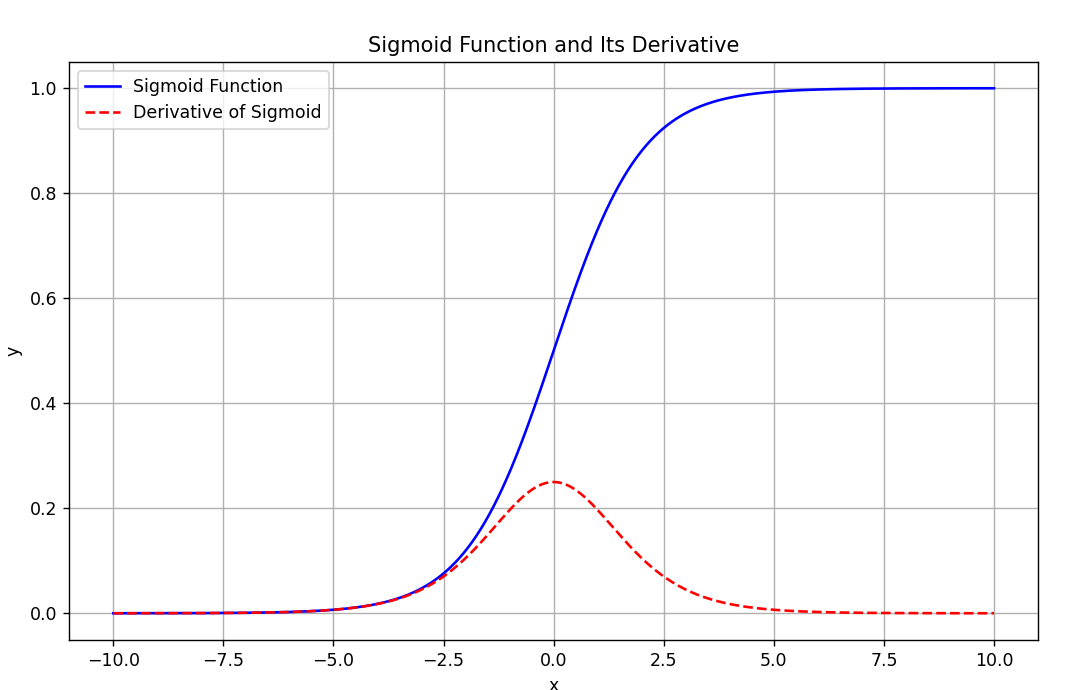
这种函数在数学里面叫做:饱和函数
当一个函数的导数在输入值趋向于正无穷或负无穷时趋近于零,该函数就被称为饱和函数。
other
BCE损失(二分类的损失函数)
loss=−(ylogy^+(1−y)log(1−y^))\operatorname{loss}=-(y \log \hat{y}+(1-y) \log (1-\hat{y}))loss=−(ylogy^+(1−y)log(1−y^))
| 真实标签 (y) | 预测概率 (y^\widehat{y}y) | BCE Loss |
|---|---|---|
| 1 | 0.2 | 1.6094 |
| 1 | 0.8 | 0.2231 |
| 0 | 0.3 | 0.3567 |
| 0 | 0.7 | 1.2040 |
Mini-Batch Loss: 0.8483
Mini-Batch Loss Function for Binary Classification:
loss =−1N∑n=1ynlogy^n+(1−yn)log(1−y^n)=-\frac{1}{N} \sum_{n=1} y_n \log \hat{y}_n+\left(1-y_n\right) \log \left(1-\hat{y}_n\right)=−N1∑n=1ynlogy^n+(1−yn)log(1−y^n)
如何使用
数据准备
x_data =torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[0],[0],[1]]) #分类
设计模型
import torch
import torch.nn.functional as F
class LogisticRegressionModel(torch.nn.Module):def __init__(self):super(LogisticRegressionModel, self).__init__()self.linear = torch.nn.Linear(1, 1)##因为sigma没有参数所以上面与之前是一样的def forward(self, x):y_pred = F.sigmoid(self.linear(x))return y_pred
model = LogisticRegressionModel()
构造损失函数 & 优化器
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
训练过程
for epoch in range(1000):y_pred = model(x_data)loss = criterion(y_pred, y_data)print(epoch, loss.item())optimizer.zero_grad()loss.backward()optimizer.step()
多维度特征的输入处理
Eg:
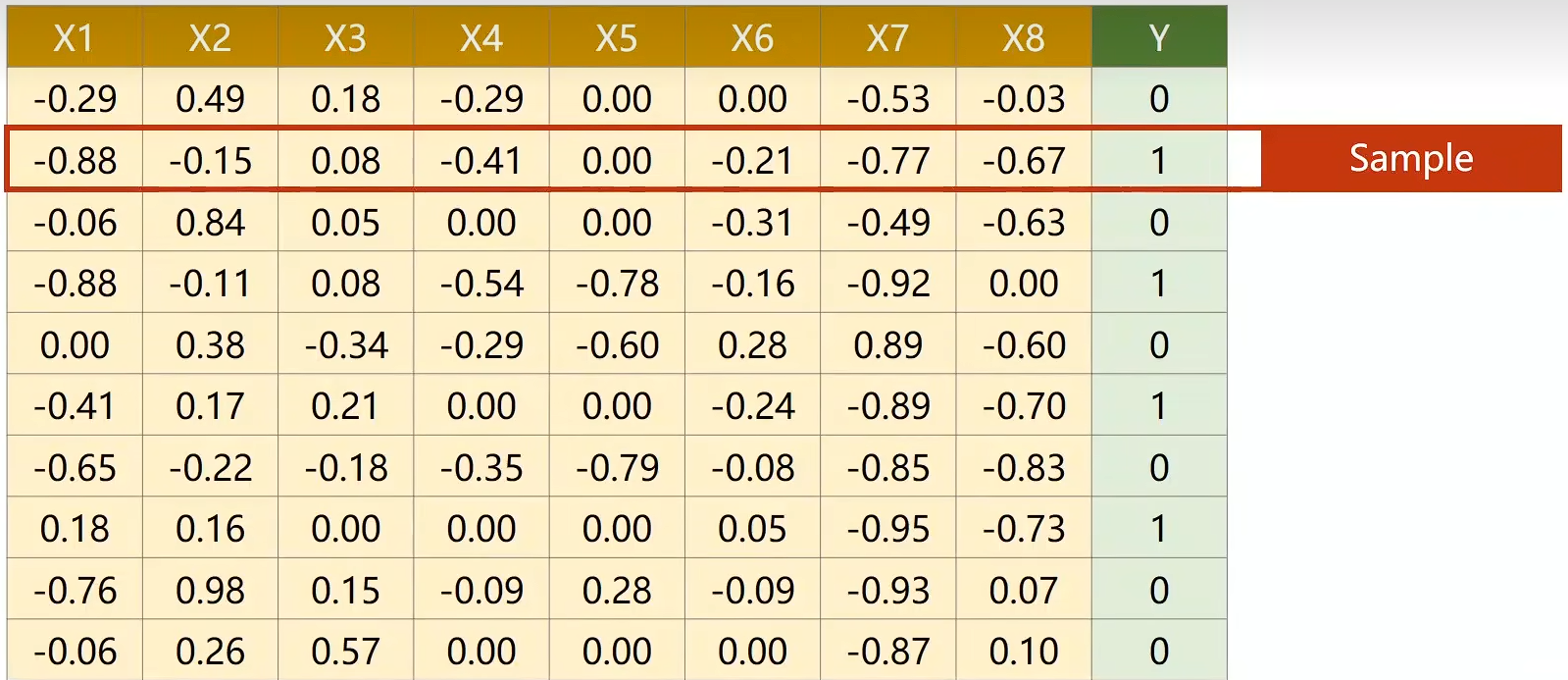
[x][y][x][y][x][y] 就是输入
Logistic Regression Model:
y^(i)=σ(x(i)∗ω+b)\hat{y}^{(i)}=\sigma\left(x^{(i)} * \omega+b\right)y^(i)=σ(x(i)∗ω+b)
y^(i)=σ(∑n=18xn(i)⋅ωn+b)\hat{y}^{(i)}=\sigma\left(\sum_{n=1}^8 x_n^{(i)} \cdot \omega_n+b\right)y^(i)=σ(∑n=18xn(i)⋅ωn+b)
∑n=18xn(i)⋅ωn=[x1(i)⋯x8(i)][ω1⋮ω8]\sum_{n=1}^8 x_n^{(i)} \cdot \omega_n=\left[\begin{array}{lll}x_1^{(i)} & \cdots & x_8^{(i)}\end{array}\right]\left[\begin{array}{c}\omega_1 \\ \vdots \\ \omega_8\end{array}\right]∑n=18xn(i)⋅ωn=[x1(i)⋯x8(i)]ω1⋮ω8
y^(i)=σ([x1(i)⋯x8(i)][ω1⋮ω8]+b)=σ(z(i))\begin{align*} \hat{\mathbf{y}}^{(i)} &= \sigma\big(\begin{bmatrix}x_1^{(i)} & \cdots & x_8^{(i)}\end{bmatrix}\begin{bmatrix}\omega_1\\\vdots\\\omega_8\end{bmatrix}+b\big) \\ &= \sigma(z^{(i)}) \end{align*} y^(i)=σ([x1(i)⋯x8(i)]ω1⋮ω8+b)=σ(z(i))
Mini-Batch
[y^(1)⋮y^(N)]=[σ(Z(1))⋮σ(Z(N))]=σ([Z(1)⋮Z(N)])\begin{bmatrix} \hat{\mathbf{y}}^{(1)} \\ \vdots \\ \hat{\mathbf{y}}^{(N)} \end{bmatrix} = \begin{bmatrix} \sigma(Z^{(1)}) \\ \vdots \\ \sigma(Z^{(N)}) \end{bmatrix} = \sigma\left(\begin{bmatrix} Z^{(1)} \\ \vdots \\ Z^{(N)} \end{bmatrix}\right) y^(1)⋮y^(N)=σ(Z(1))⋮σ(Z(N))=σZ(1)⋮Z(N)
Z(1)=[x1(1)⋯x8(1)][ω1⋮ω8]+bZ(N)=[x1(N)⋯x8(N)][ω1⋮ω8]+b\begin{aligned} Z^{(1)} &= \begin{bmatrix} x_1^{(1)} & \cdots & x_8^{(1)} \end{bmatrix} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix} + b \\ Z^{(N)} &= \begin{bmatrix} x_1^{(N)} & \cdots & x_8^{(N)} \end{bmatrix} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix} + b \end{aligned}Z(1)Z(N)=[x1(1)⋯x8(1)]ω1⋮ω8+b=[x1(N)⋯x8(N)]ω1⋮ω8+b
[Z(1)⋮Z(N)]=[x1(1)⋯x8(1)⋮⋱⋮x1(N)⋯x8(N)][ω1⋮ω8]+[b⋮b]\begin{bmatrix} Z^{(1)} \\ \vdots \\ Z^{(N)} \end{bmatrix} = \begin{bmatrix} x_1^{(1)} & \cdots & x_8^{(1)} \\ \vdots & \ddots & \vdots \\ x_1^{(N)} & \cdots & x_8^{(N)} \end{bmatrix} \begin{bmatrix} \omega_1 \\ \vdots \\ \omega_8 \end{bmatrix} + \begin{bmatrix} b \\ \vdots \\ b \end{bmatrix} Z(1)⋮Z(N)=x1(1)⋮x1(N)⋯⋱⋯x8(1)⋮x8(N)ω1⋮ω8+b⋮b
class Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.linear = torch.nn.Linear(8, 1) #维度self.sigmoid = torch.nn.Sigmoid()def forward(self, x):x = self.sigmoid(self.linear(x))return xmodel = Model()
Eg:
import torchclass Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.linear1 = torch.nn.Linear(8, 6)self.linear2 = torch.nn.Linear(6, 4)self.linear3 = torch.nn.Linear(4, 1)self.sigmoid = torch.nn.Sigmoid()def forward(self, x):x = self.sigmoid(self.linear1(x))x = self.sigmoid(self.linear2(x))x = self.sigmoid(self.linear3(x))return xmodel = Model()
现在这是一个完整的 PyTorch 神经网络模型代码。这个模型包含:
- 3个全连接层:8→6→4→1
- 每层后都使用 Sigmoid 激活函数
- 最终输出一个标量值
损失 & 优化器没有变化
criterion = torch.nn.BCELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
训练
for epoch in range(100):# Forwardy_pred = model(x_data)loss = criterion(y_pred, y_data)print(epoch, loss.item())# Backwardoptimizer.zero_grad()loss.backward()# Updateoptimizer.step()
注意这里使用的仍然是Batch而不是Mini-Batch
NOTICE:
This program has not use Mini-Batchfor training.
We shall talk about DataLoader later.
加载数据集
Dataset and DataLoader
Dataset 和 DataLoader 是 PyTorch 中用于数据加载和处理的核心组件
# Training cycle
for epoch in range(training_epochs):# Loop over all batchesfor i in range(total_batch): #Mini-Batch
一些定义
Epoch定义
对所有训练样本进行一次前向传播(前馈)和一次反向传播(反馈)
Batch-Size
一次前向传播和反向传播中的训练样本数量
Iteration
每次迭代使用 [批量大小] 数量的示例,进行的遍历次数
Eg:
10000个样本
Batch-Size = 1000
Iteration = 10
DataLoader: batch_size = 2, shuffle = True
其中 shuffle = True 表示需要打乱顺序

- 第一步进行Shuffle
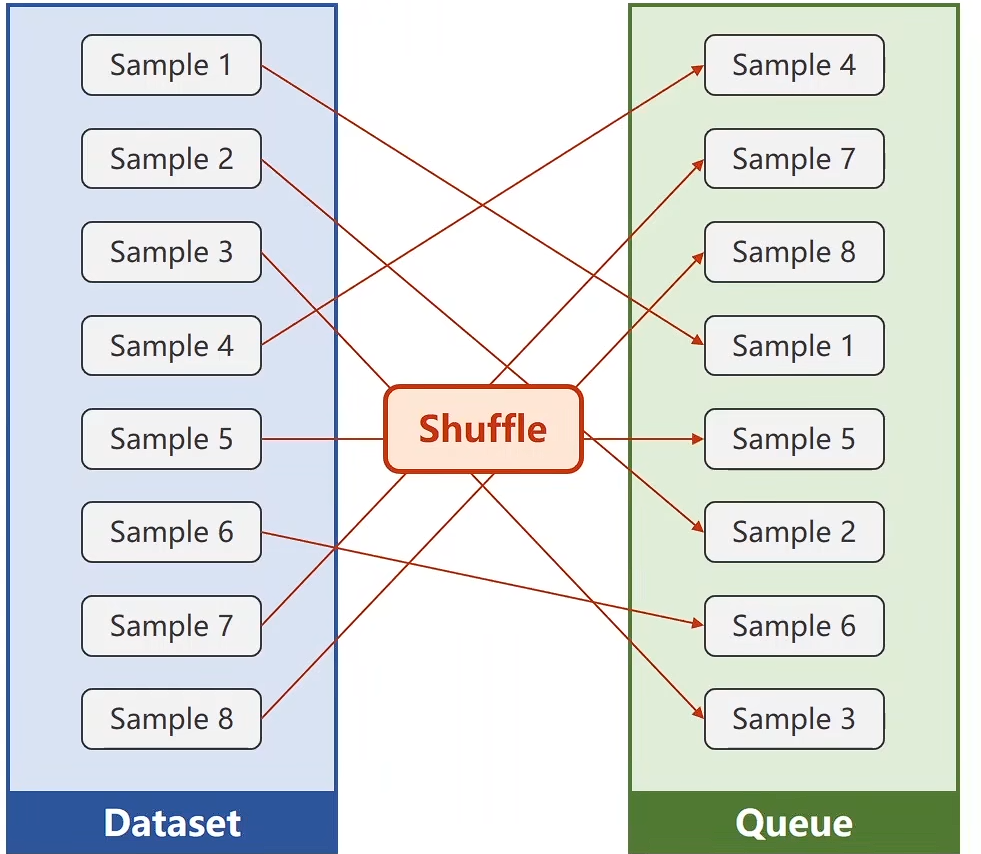
-
第二步进行分组
Batch_Size = 2
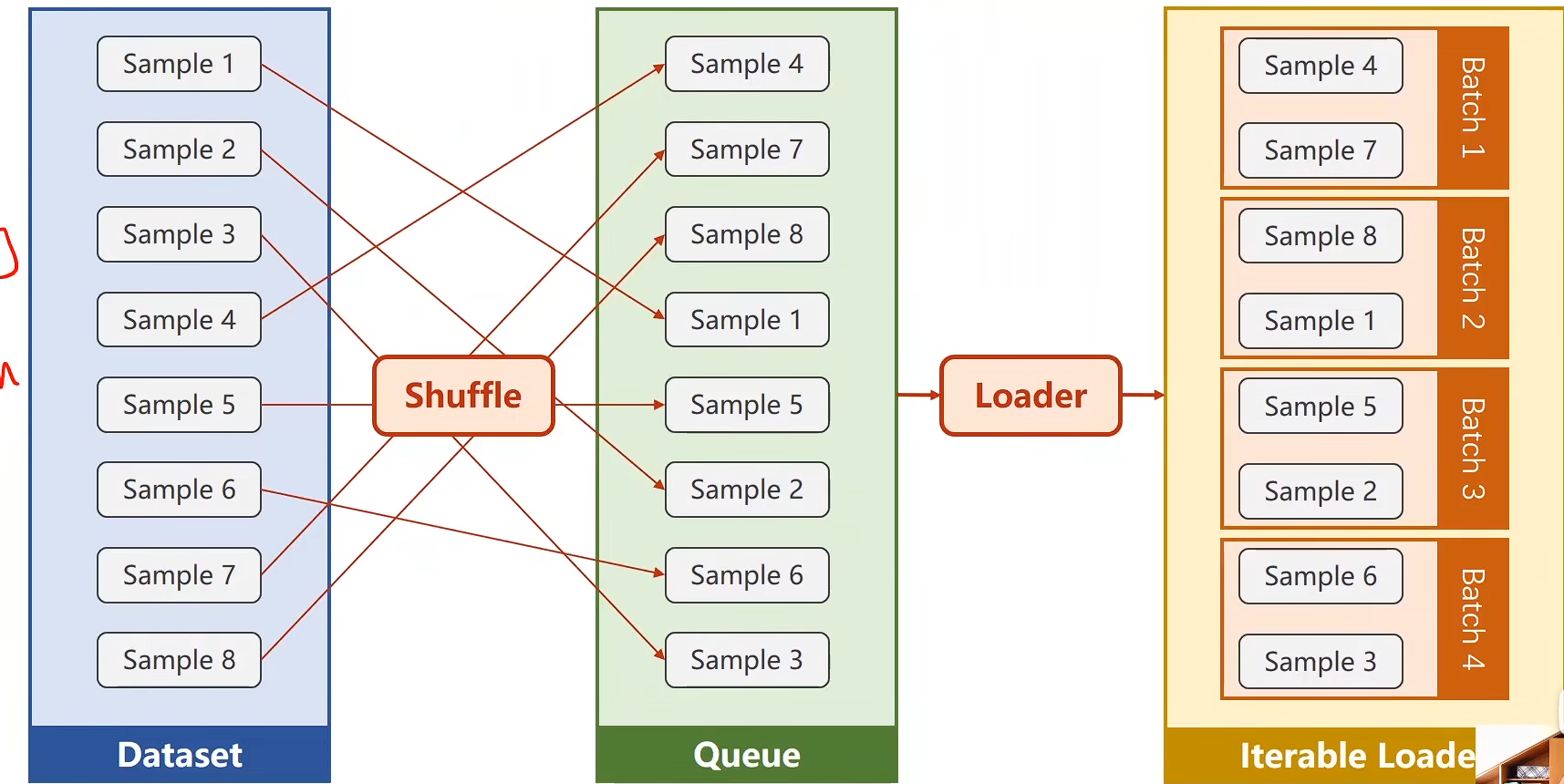
代码实现
import torch
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
# DataLoader是一个帮助我们在PyTorch中加载数据的类
# Dataset一个抽象类,我们可以定义一个继承自该类的子类
class DiabetesDataset(Dataset): #DiabetesDataset继承自抽象类 数据集def __init__(self):passdef __getitem__(self, index): #表达式dataset[index]将调用这个魔术函数,通过索引把数据拿到passdef __len__(self): #这个魔术函数返回数据集的长度pass
'''
在构建这个数据集的时候,一般有两种选择
1. 在 init 的时候我们把所有的数据都读到内存里面(适合数据不大的)
2. 定义一个列表把数据的地址放进去,等getitem读取的时候现去文件里读出来再返回
'''
dataset = DiabetesDataset()
train_loader = DataLoader(dataset=dataset, #传递数据集batch_size=32, #一个小批量的容量是多少shuffle=True, #是否要打乱num_workers=2) #读的是否需要多线程(并行化),需要几个进程
注意:多进程的实现方式在Windows上有所不同,它使用的是spawn而不是fork,所有运行的时候可能会出现问题
如何解决?
if __name__=='_main_': #添加这个#下面放主程序for epoch in range(100)for i, data in enumerate(train_loader, 0)# 1. Prepare data
多进程安全(就是刚才遇到的问题)
在 Windows 系统下使用多进程时,必须要有这个保护,否则子进程会重复执行主模块代码。
主要步骤
- 准备数据集 (主要改动)
- 使用继承自nn.Module的类设计模型
- 使用PyTorch API构建损失和优化器
- 训练周期 前馈、反馈、更新 (主要改动)
完整代码
import numpy as np
import torch
from torch.utils.data import Dataset
from torch.utils.data import DataLoaderclass DiabetesDataset(Dataset):def __init__(self, filepath):xy = np.loadtxt(filepath, delimiter=',', dtype=np.float32)self.len = xy.shape[0] #(N,9) 第一个就是样本数量self.x_data = torch.from_numpy(xy[:, :-1])self.y_data = torch.from_numpy(xy[:, [-1]])def __getitem__(self, index):return self.x_data[index], self.y_data[index]def __len__(self):return self.lenclass Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.linear1 = torch.nn.Linear(8, 6)self.linear2 = torch.nn.Linear(6, 4)self.linear3 = torch.nn.Linear(4, 1)self.sigmoid = torch.nn.Sigmoid()def forward(self, x):x = self.sigmoid(self.linear1(x))x = self.sigmoid(self.linear2(x))x = self.sigmoid(self.linear3(x))return xif __name__=='__main__': #添加这个dataset = DiabetesDataset('diabetes.csv.gz')train_loader = DataLoader(dataset=dataset,batch_size=32,shuffle=True,num_workers=2)model = Model()criterion = torch.nn.BCELoss(size_average=True)optimizer = torch.optim.SGD(model.parameters(), lr=0.01)for epoch in range(100):for i, data in enumerate(train_loader, 0): #(可迭代对象,起始索引)# 1.Prepare datainputs, labels = data# 2. Forwardy_pred = model(inputs)loss = criterion(y_pred, labels)print(epoch, i, loss.item())# 3. Backwardoptimizer.zero_grad()loss.backward()# 4. Updateoptimizer.step()
shape[0]是第 0 维的大小,即样本的数量(行数)。shape[1]是第 1 维的大小,即每个样本的特征数量(列数)。
多分类问题
相比二分类我们要改变一下
P(y=1)=0.8P(y=1) = 0.8P(y=1)=0.8
P(y=2)=0.6P(y=2) = 0.6P(y=2)=0.6
P(y=3)=0.9P(y=3) = 0.9P(y=3)=0.9
… …
这种存在相互矛盾,就比如 y=1y = 1y=1 与 y=2y = 2y=2
所以我们应该让概率和等于1,相当于引入竞争机制
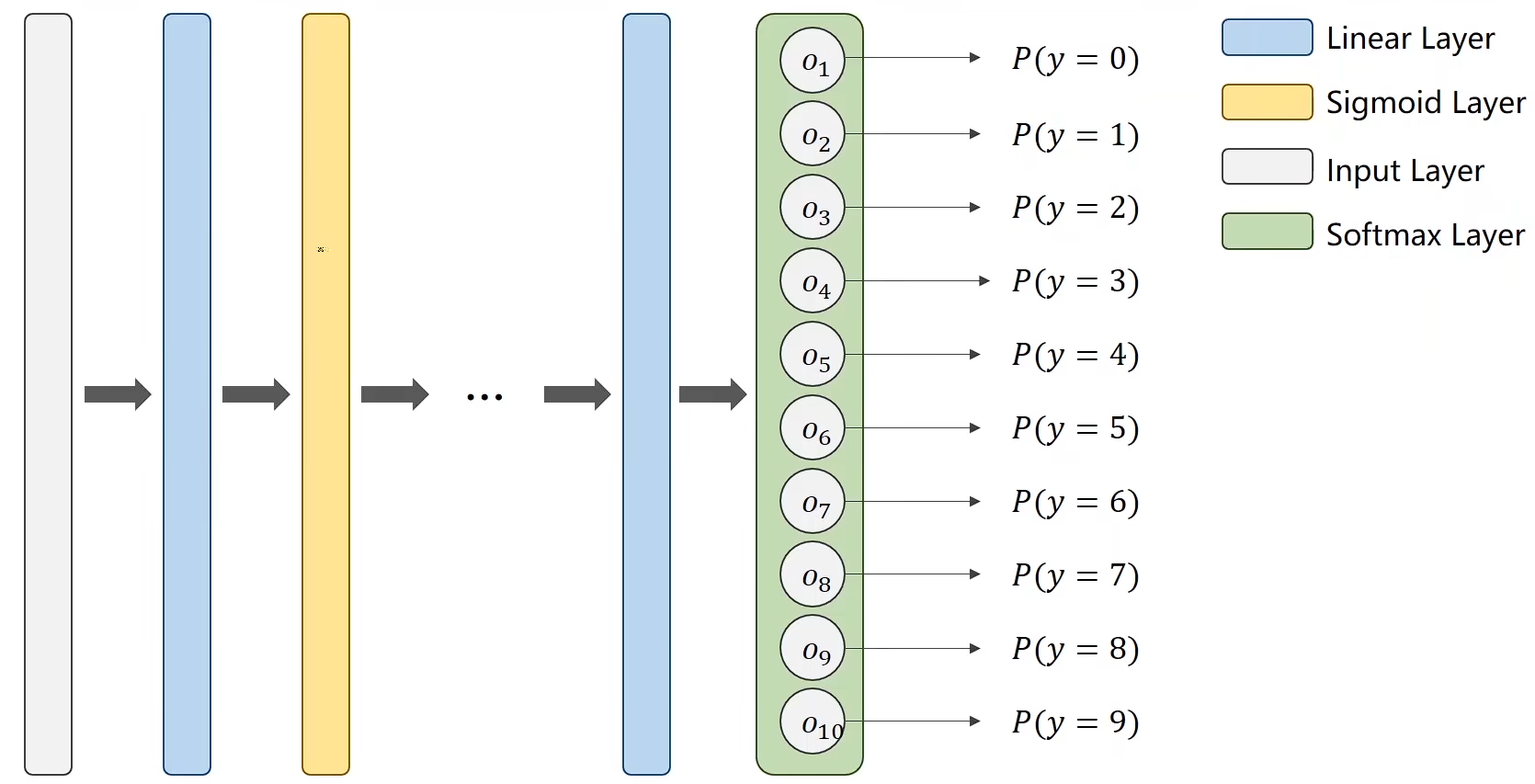
因此在最后一层使用 Softmax Later,他可以满足两个条件:
- 每一个输出都是 ≥0\geq 0≥0
- 概率和等于1
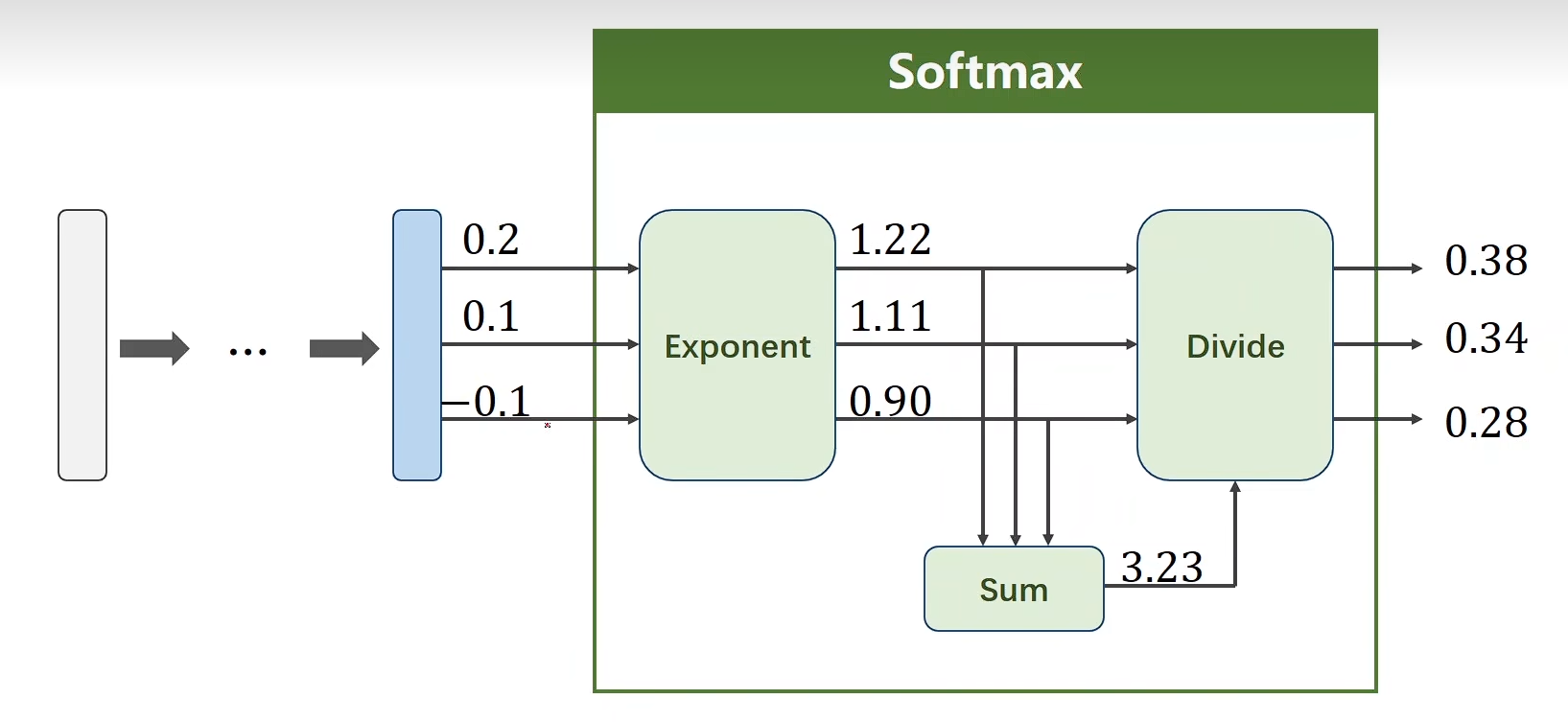
Softmax
P(y=i)=∣ezi∣∑j=0K−1ezj,i∈{0,...,K−1}P(y = i) = \frac{\left| e^{z_i} \right|}{\sum_{j=0}^{K-1} e^{z_j}}, \quad i \in \{0, ..., K-1\}P(y=i)=∑j=0K−1ezj∣ezi∣,i∈{0,...,K−1}
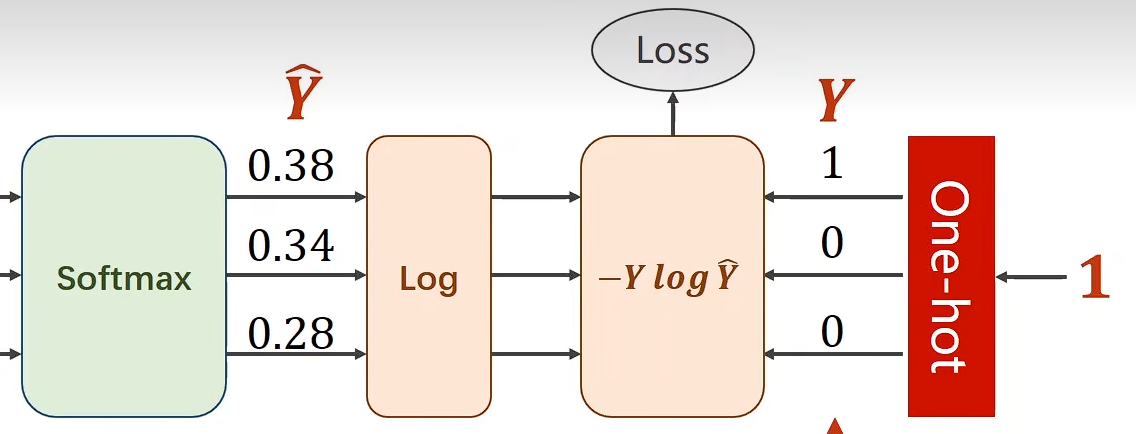
Loss
Loss(Y,Y^)=−Ylog(Y^)\text{Loss}(Y, \hat{Y}) = -Y \log(\hat{Y})Loss(Y,Y^)=−Ylog(Y^)
import numpy as np
y = np.array([1, 0, 0])
z = np.array([0.2, 0.1, -0.1])
y_pred = np.exp(z) / np.exp(z).sum()
loss = (-y * np.log(y_pred)).sum()
print(loss)
交叉熵损失
Torch.nn.CrossEntropyLoss()
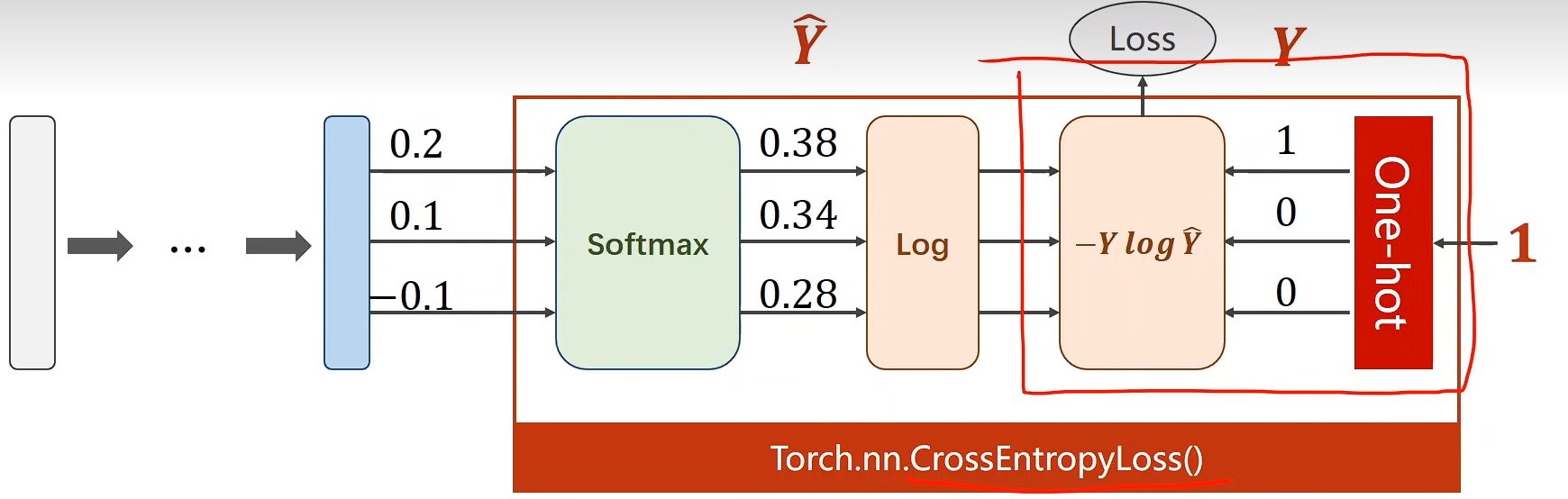
注意:最后一步不需要进行非线性变化直接给交叉熵损失函数即可,因为这个函数里面就有Softmax
import torch
y = torch.LongTensor([0])
z = torch.Tensor([[0.2, 0.1, -0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z, y)
print(loss)
import torch
criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2, 0, 1])Y_pred1 = torch.Tensor([[0.1, 0.2, 0.9],[1.1, 0.1, 0.2],[0.2, 2.1, 0.1]])
Y_pred2 = torch.Tensor([[0.8, 0.2, 0.3],[0.2, 0.3, 0.5],[0.2, 0.2, 0.5]])l1 = criterion(Y_pred1, Y)
l2 = criterion(Y_pred2, Y)
print('\t',l1.data, '\t', l2.data)
# tensor(0.4966) tensor(1.2389)
LogSoftmax和NLLLoss
- LogSoftmax
- 所在位置:
torch.nn.LogSoftmax - 作用:对网络输出(logits)做 softmax,再取对数。
- 输入:通常是未经过归一化的 logits(shape:
[batch_size, num_classes])。 - 输出:对数概率(log-probabilities),shape 和输入一致。
公式:
LogSoftmax(xi)=log(exi∑jexj)\text{LogSoftmax}(x_i) = \log\left(\frac{e^{x_i}}{\sum_j e^{x_j}}\right) LogSoftmax(xi)=log(∑jexjexi)
特点:
- 输出的是 对数形式的概率。
- 常和
NLLLoss搭配,因为NLLLoss需要输入 log-prob。
- NLLLoss (Negative Log Likelihood Loss)
- 所在位置:
torch.nn.NLLLoss - 作用:计算 负对数似然损失,用来训练分类模型。
- 输入:
input:log-probabilities(一般来自LogSoftmax,shape:[batch_size, num_classes])。target:类别标签(shape:[batch_size],值是类别下标)。
- 输出:一个标量 loss。
公式:
对于单一样本:
NLLLoss(x,y)=−input[y]\text{NLLLoss}(x, y) = - \text{input}[y] NLLLoss(x,y)=−input[y]
也就是取正确类别 y 的 log-prob,然后加个负号。
- 两者的关系
LogSoftmax把 logits 转换为 对数概率分布。NLLLoss取目标类别对应的对数概率,取负号,做平均。
因此:
- 常见组合是
LogSoftmax + NLLLoss。 - 为了方便,PyTorch 提供了
CrossEntropyLoss,它 =LogSoftmax + NLLLoss的合体,不需要手动分开写。
图像处理
transforms
from torchvision import transforms
from torchvision import transforms# 定义一个常见的图像预处理流水线
transform = transforms.Compose([transforms.Resize(256), # 调整大小transforms.CenterCrop(224), # 中心裁剪transforms.ToTensor(), # 转换为Tensor,并将像素值从[0,255]缩放到[0,1]transforms.Normalize(mean=[0.485, 0.456, 0.406], # ImageNet数据集的RGB均值std=[0.229, 0.224, 0.225] # ImageNet数据集的RGB标准差)
])# 然后将这个 transform 应用到你的图像上
# from PIL import Image
# image = Image.open("path_to_image.jpg").convert('RGB')
# input_tensor = transform(image)
这里的 mean 和 std 不是随便设定的,它们应该是你所使用的训练数据集的统计值。
-
使用预训练模型:如果你在使用在大型数据集(如 ImageNet)上预训练的模型,必须使用该数据集提供的标准值。这是因为预训练模型的权重是基于这些统计值学习得到的。PyTorch官方推荐的ImageNet统计值就是上面例子中的:
mean = [0.485, 0.456, 0.406]std = [0.229, 0.224, 0.225]
-
在自己的数据集上训练:如果你是从头开始训练模型,那么你应该计算自己训练集的均值和标准差。计算方法如下:
python
# 假设你的训练数据加载器是 train_loader # 数据已经是 ToTensor() 后的,范围在 [0,1]channels_sum, channels_squared_sum, num_batches = 0, 0, 0 for data, _ in train_loader:# 按维度 (0, 2, 3) 计算均值和平方均值# 即:对每个通道,在所有批次、所有高度、所有宽度上求和channels_sum += torch.mean(data, dim=[0,2,3])channels_squared_sum += torch.mean(data**2, dim=[0,2,3])num_batches += 1mean = channels_sum / num_batches # 方差 = E(X^2) - [E(X)]^2 std = (channels_squared_sum / num_batches - mean ** 2) ** 0.5print("Mean:", mean) print("Std:", std)
总结
| 特性 | 说明 |
|---|---|
| 功能 | 对图像张量进行标准化,使其各通道数据变为均值为0、标准差为1的分布。 |
| 公式 | output = (input - mean) / std |
| 目的 | 加速模型收敛,提升训练稳定性,提高模型性能。 |
| 使用顺序 | 必须在 ToTensor() 之后。 |
| 参数选择 | 使用预训练模型时,遵循模型训练时的统计值(如ImageNet的统计值)。自己训练时,计算自己数据集的统计值。 |
| 可视化 | 需要反标准化操作才能正确显示。 |
view()
view() 函数的目的是改变张量的形状(shape),也就是重构(reshape) 张量,而不改变其实际的数据内容。它相当于 NumPy 中的 reshape() 操作。
关键特性: view() 返回的是一个新视图(new view),这意味着返回的张量与原始张量共享底层数据存储。修改新张量会影响原始张量,反之亦然。
new_tensor = tensor.view(*shape)
-
tensor:要进行形状变换的原始张量。 -
*shape:目标形状。可以是一个整数序列,也可以是多个整数参数。
使用 -1 自动计算维度
-1 是一个非常有用的占位符,它表示 “请自动计算这个维度的大小,以保证总元素个数不变”。
规则很简单:新形状中所有维度的乘积必须等于原始张量的总元素数。
例如,一个包含 12 个元素的张量:
view(3, 4)-> 3*4=12view(2, -1)-> 2*6=12 (系统自动算出是6)view(-1, 3)-> 4*3=12 (系统自动算出是4)view(2, 2, -1)-> 223=12 (系统自动算出是3)
注意: 在形状参数中,最多只能有一个 -1。
Minist
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim #关于构建关键优化器
class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.l1 = torch.nn.Linear(784, 512)self.l2 = torch.nn.Linear(512, 256)self.l3 = torch.nn.Linear(256, 128)self.l4 = torch.nn.Linear(128, 64)self.l5 = torch.nn.Linear(64, 32)self.l6 = torch.nn.Linear(32, 10)def forward(self, x):x = x.view(-1, 784)x = F.relu((self.l1(x)))x = F.relu((self.l2(x)))x = F.relu((self.l3(x)))x = F.relu((self.l4(x)))x = F.relu((self.l5(x)))return self.l6(x)
#下载数据 & 原始图像处理
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), #将 PIL图像转换成张量 Tensortransforms.Normalize((0.1307, ), (0.3081, )) #单通道灰度图片# 核心作用是对张量(通常是图像张量)进行标准化(或称归一化)
])
'''
datasets.MNIST 内部已经实现了 Dataset 类!您可以把它想象成:
# torchvision.datasets.mnist.py 内部的简化实现
class MNIST(VisionDataset):def __init__(self, root, train=True, transform=None, target_transform=None, download=False):super().__init__(root, transform=transform, target_transform=target_transform)self.train = trainself.data, self.targets = self._load_data()def __getitem__(self, index):img = self.data[index]target = self.targets[index]# 转换为PIL图像img = Image.fromarray(img.numpy(), mode='L')# 应用transformif self.transform is not None:img = self.transform(img)return img, targetdef __len__(self):return len(self.data)
'''
train_dataset = datasets.MNIST(root='./dataset/mnist/',train=True,download=True,transform=transform)
train_loader = DataLoader(train_dataset,batch_size=batch_size,shuffle=True)
test_dataset = datasets.MNIST(root='./dataset/mnist/',train=False,download=True,transform=transform)
test_loader = DataLoader(test_dataset,shuffle=False,batch_size=batch_size)model = Net()
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) #引入动量 带动量的随机梯度下降(SGD with Momentum)def train(epoch):running_loss = 0.0for batch_idx, data in enumerate(train_loader, 0):inputs, target = dataoptimizer.zero_grad()output = model(inputs)loss = criterion(output, target)loss.backward()optimizer.step()running_loss += loss.item()if batch_idx % 300 == 299:print('[%d, %5d] loss: %.3f' %(epoch+1, batch_idx + 1, running_loss / 300))running_loss = 0.0def test():correct = 0total = 0with torch.no_grad():for data in test_loader:images, labels = dataoutputs = model(images)_, predicted = torch.max(outputs, dim = 1)total += labels.size(0)correct += (predicted == labels).sum().item()print('Accuracy on test set: %d %%' % (100 * correct / total))if __name__=='__main__':for epoch in range(10):train(epoch)test()
卷积神经网络 CNN(基础篇)
CNN 与 DNN 对比
CNN是为处理具有网格状拓扑结构的数据(如图像)而专门设计的,它通过“卷积”操作高效地提取空间特征;而DNN是一种通用的网络结构,它将输入数据视为一维向量,忽略了空间信息。
| 特性 | 卷积神经网络 (CNN) | 全连接神经网络 (DNN) |
|---|---|---|
| 核心思想 | 局部连接 和 权重共享。一个神经元只连接输入数据的局部区域(如图像的一小块),并且使用同一组权重(卷积核)在整个输入上滑动扫描。 | 全局连接。相邻层的每一个神经元都与上一层的所有神经元相连。 |
| 处理数据方式 | 保持空间结构。将数据(如图像)视为二维或三维的网格结构进行处理。 | 破坏空间结构。必须将输入数据(如图像)展平 成一个一维长向量,丢失了所有的空间信息。 |
| 参数数量 | 相对较少。由于局部连接和权重共享,大大减少了需要学习的参数数量。 | 极其庞大。随着输入尺寸和网络深度的增加,参数数量会爆炸性增长,容易导致过拟合和计算困难。 |
| 主要应用领域 | 图像处理(分类、检测、分割)、视频分析、自然语言处理(文本分类、机器翻译)等。 | 通用,但在处理图像等高维数据时效率低下。常用于表格数据、简单的分类和回归任务。 |
| 特征提取方式 | 自动、分层提取。浅层网络学习边缘、角落等低级特征;深层网络组合低级特征形成纹理、物体部件等更高级别的特征。 | 手动或依赖网络自己学习。如果输入是原始像素,网络需要从零开始学习所有特征组合,效率低且困难。 |
| 平移不变性 | 天生具备。同一个物体在图像的不同位置,CNN都能识别出来,因为卷积核是滑动工作的。 | 不具备。一个物体如果移动了位置,对于展平后的输入向量来说,像素的排列完全不同,网络可能认为这是一个新模式。 |
CNN
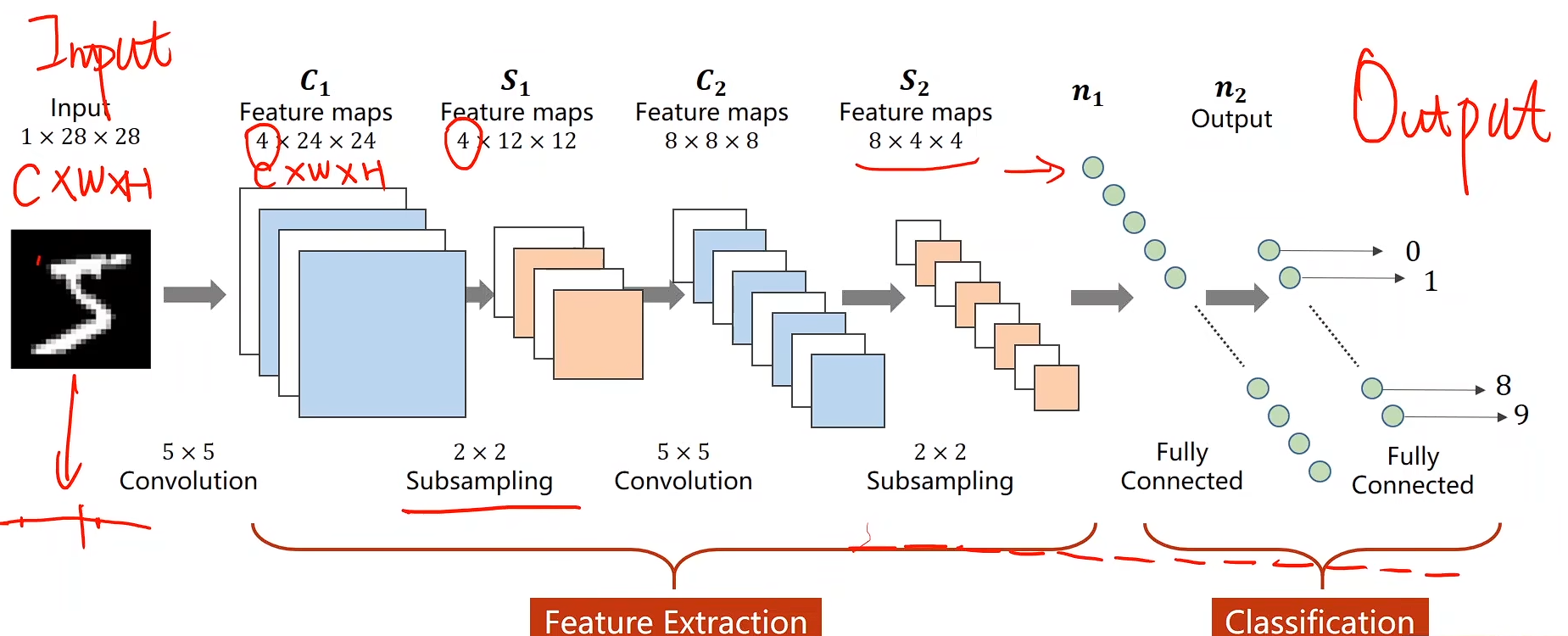
单通道
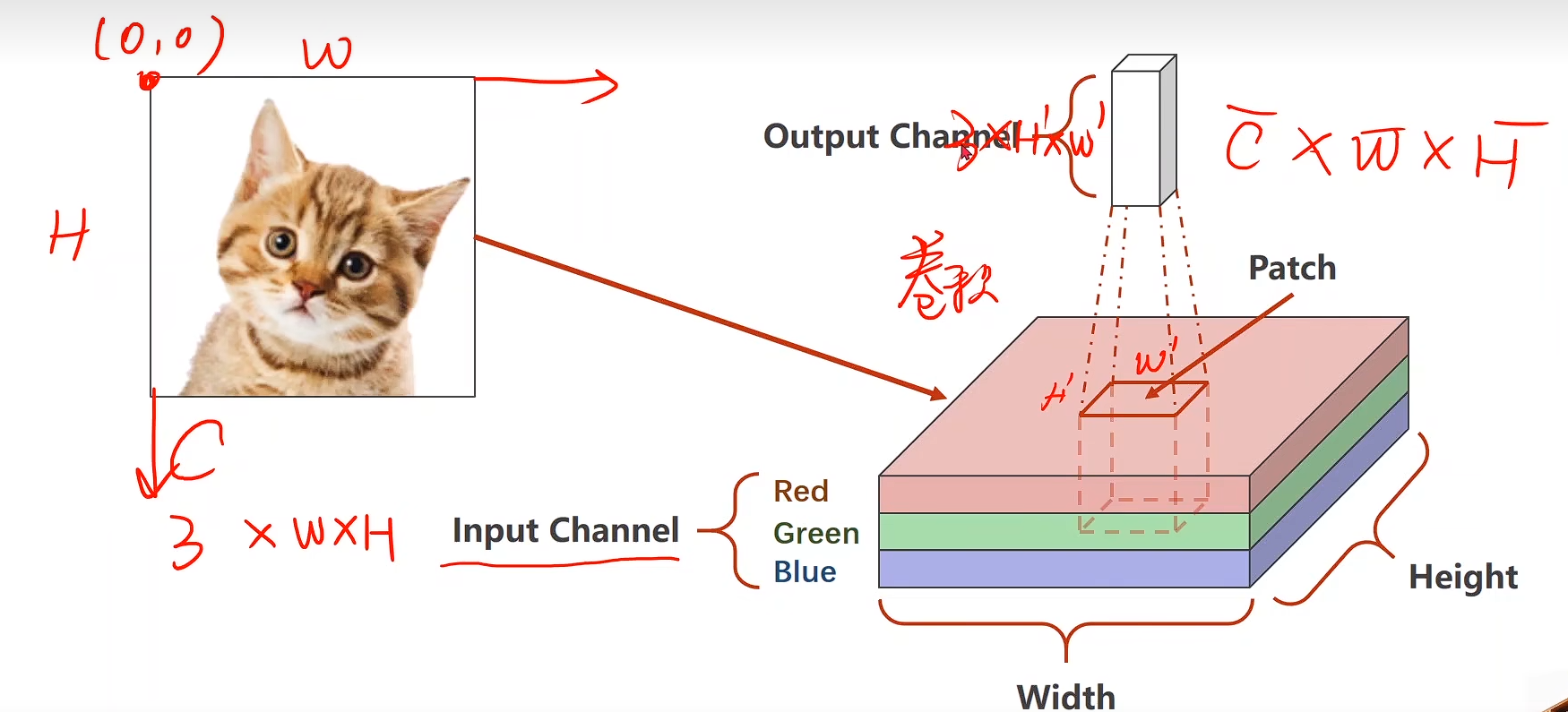
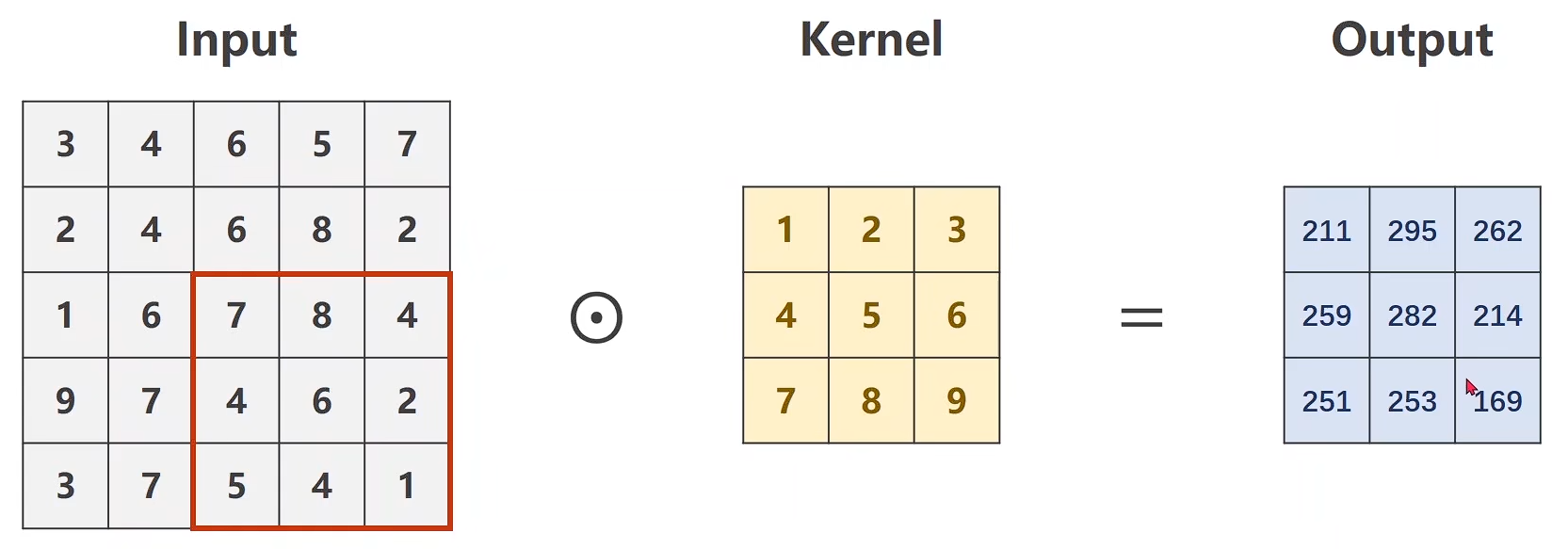
多通道(3通道为例)
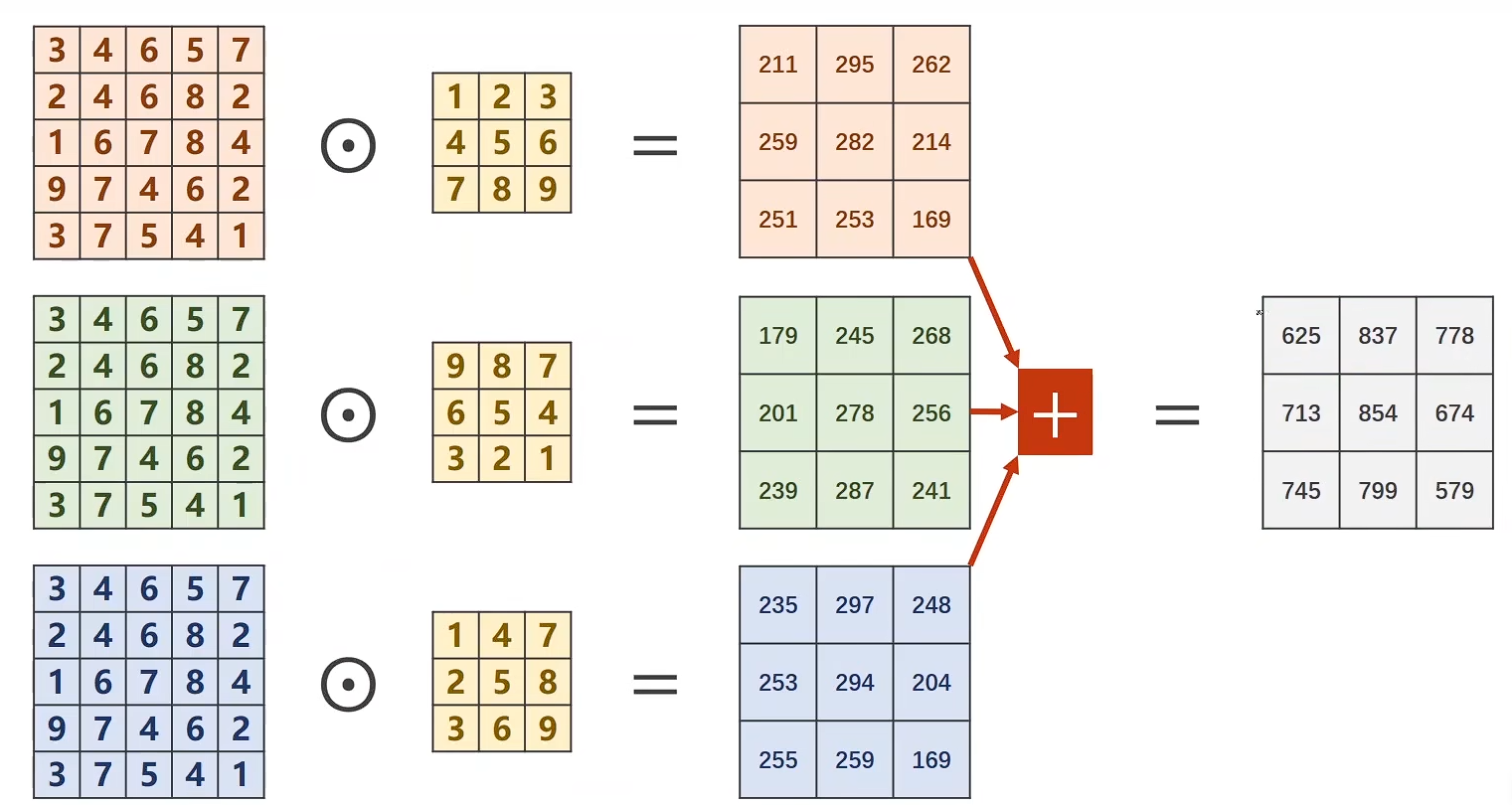
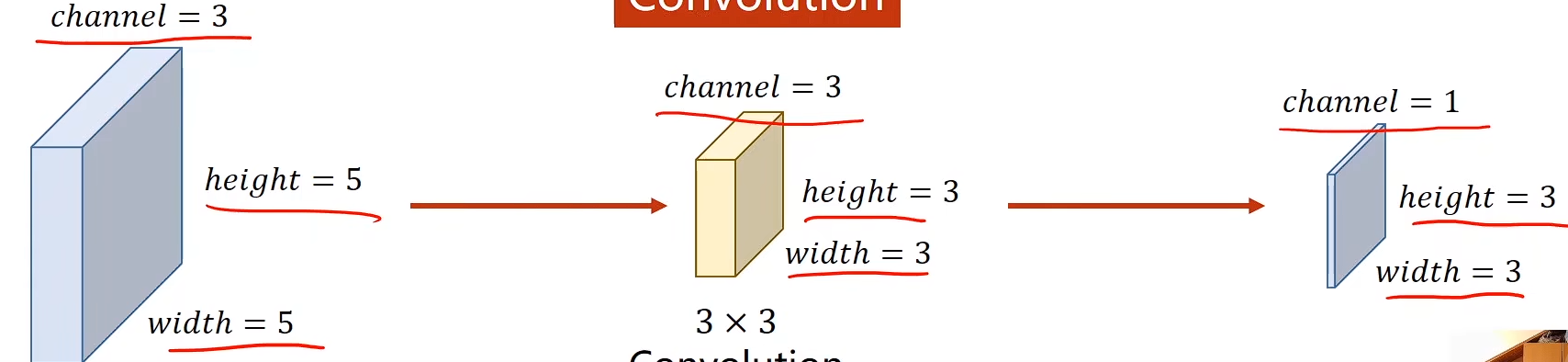
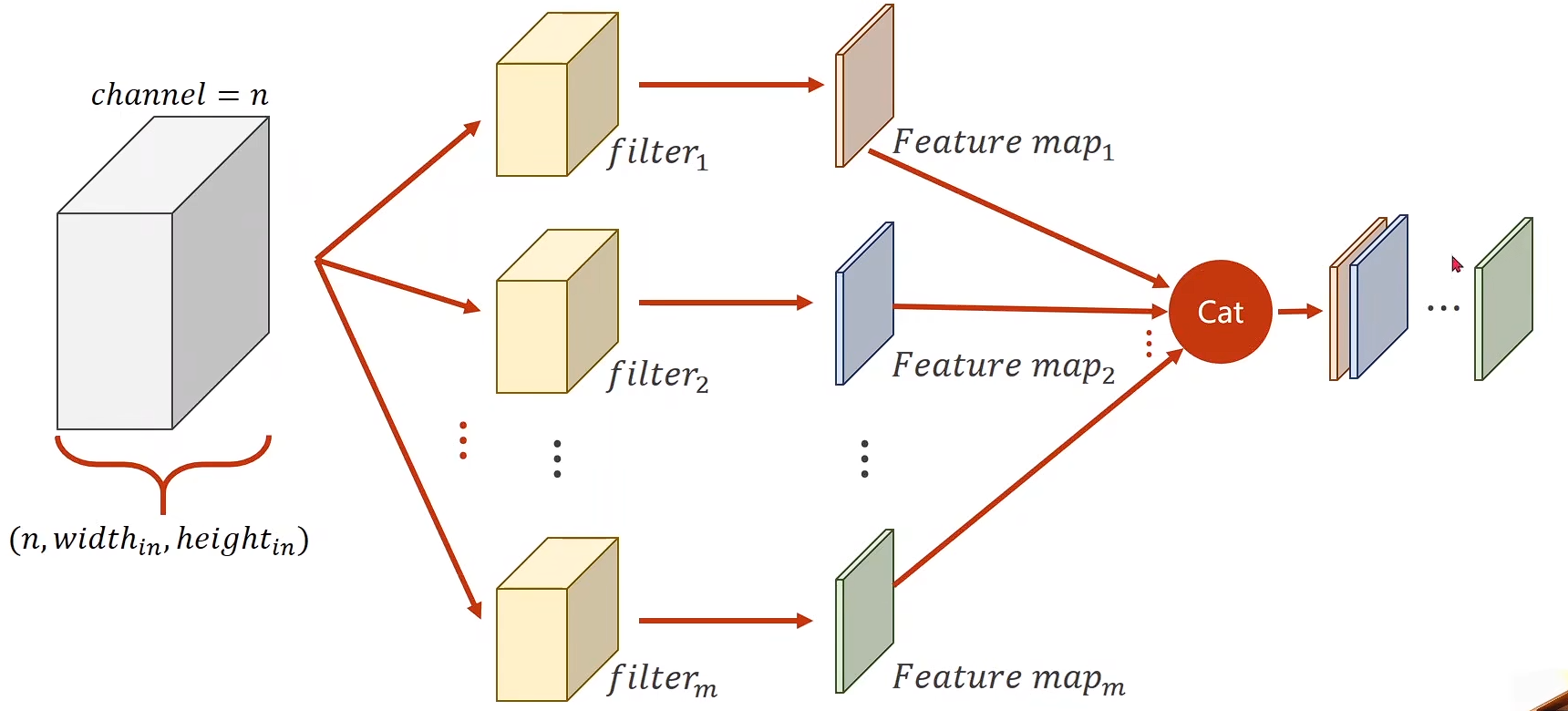
权重维度

import torch
in_channels, out_channels = 5, 10
width, height = 100, 100
kernel_size = 3
batch_size = 1input = torch.randn(batch_size,in_channels,width,height)
conv_layer = torch.nn.Conv2d(in_channels,out_channels,kernel_size)
output = conv_layer(input)print(input.shape)
print(output.shape)
print(conv_layer.weight.shape)
padding
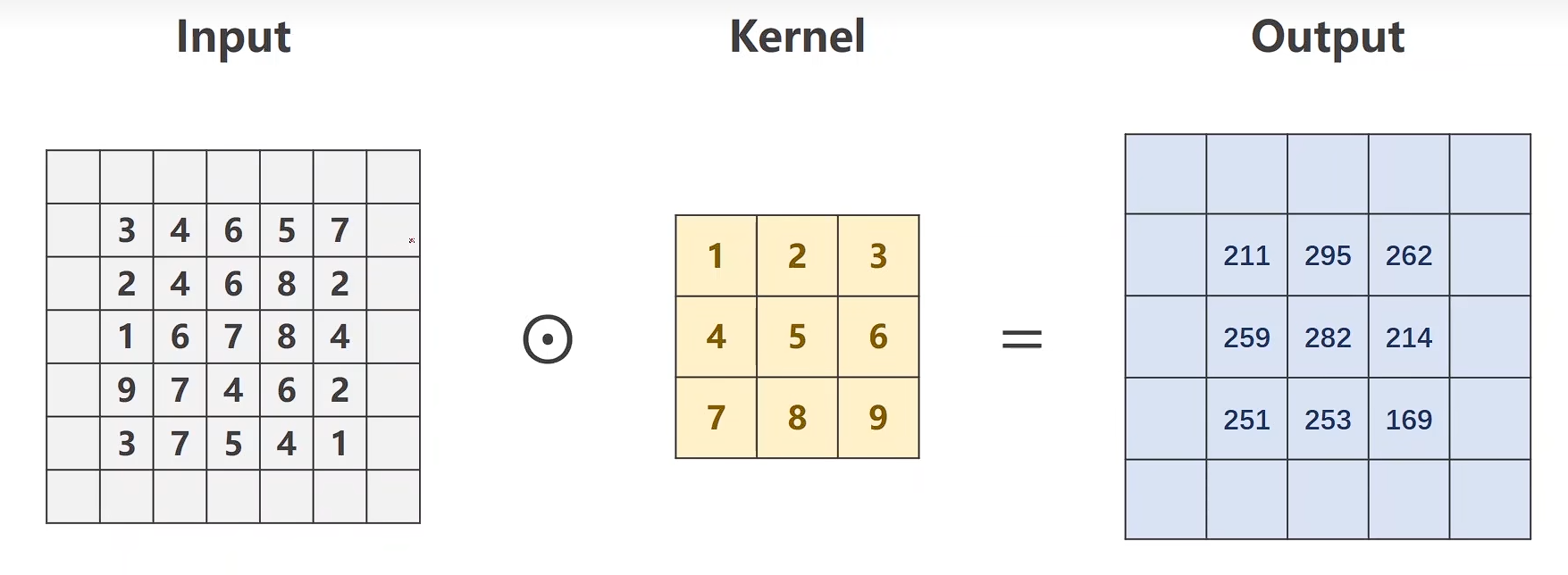
import torch
input = [3, 4, 6, 5, 7,2, 4, 6, 8, 2,1, 6, 7, 8, 4,9, 7, 4, 6, 2,3, 7 ,5, 4, 1]
input = torch.Tensor(input).view(1, 1, 5, 5) #B C W Hconv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, padding=1, bias=False)kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]).view(1, 1, 3, 3) #O I W H
conv_layer.weight.data = kernel.dataoutput = conv_layer(input)
print(output)
padding小技巧:
padding = kernel_size / 2 整除
stride
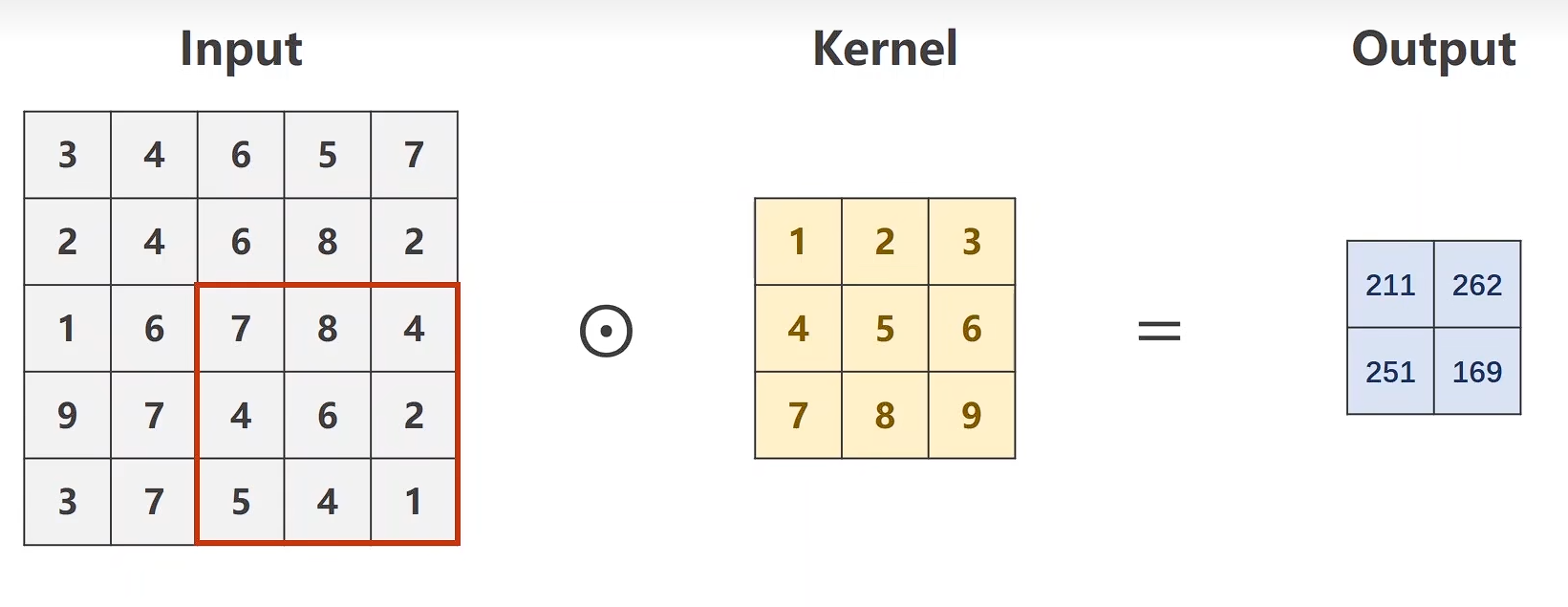
import torch
input = [3, 4, 6, 5, 7,2, 4, 6, 8, 2,1, 6, 7, 8, 4,9, 7, 4, 6, 2,3, 7 ,5, 4, 1]
input = torch.Tensor(input).view(1, 1, 5, 5) #B C W Hconv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, stride=2, bias=False)kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8, 9]).view(1, 1, 3, 3) #O I W H
conv_layer.weight.data = kernel.dataoutput = conv_layer(input)
print(output)
下采样
MaxPooling
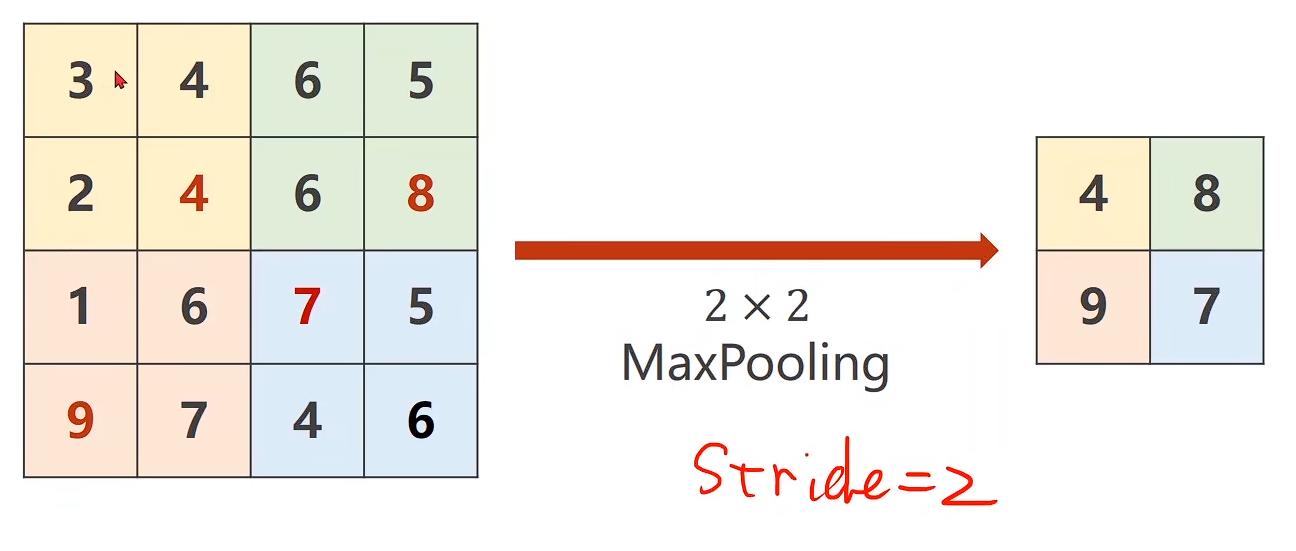
import torch
input = [3, 4, 6, 5,2, 4, 6, 8,1, 6, 7, 5,9, 7, 4, 6,]
input = torch.Tensor(input).view(1, 1, 4, 4) #B C W Hmaxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)output = maxpooling_layer(input)
print(output)
输出高度 = (输入高度 + 2×padding - kernel_size) / stride + 1
输出宽度 = (输入宽度 + 2×padding - kernel_size) / stride + 1
手写数字(实例)
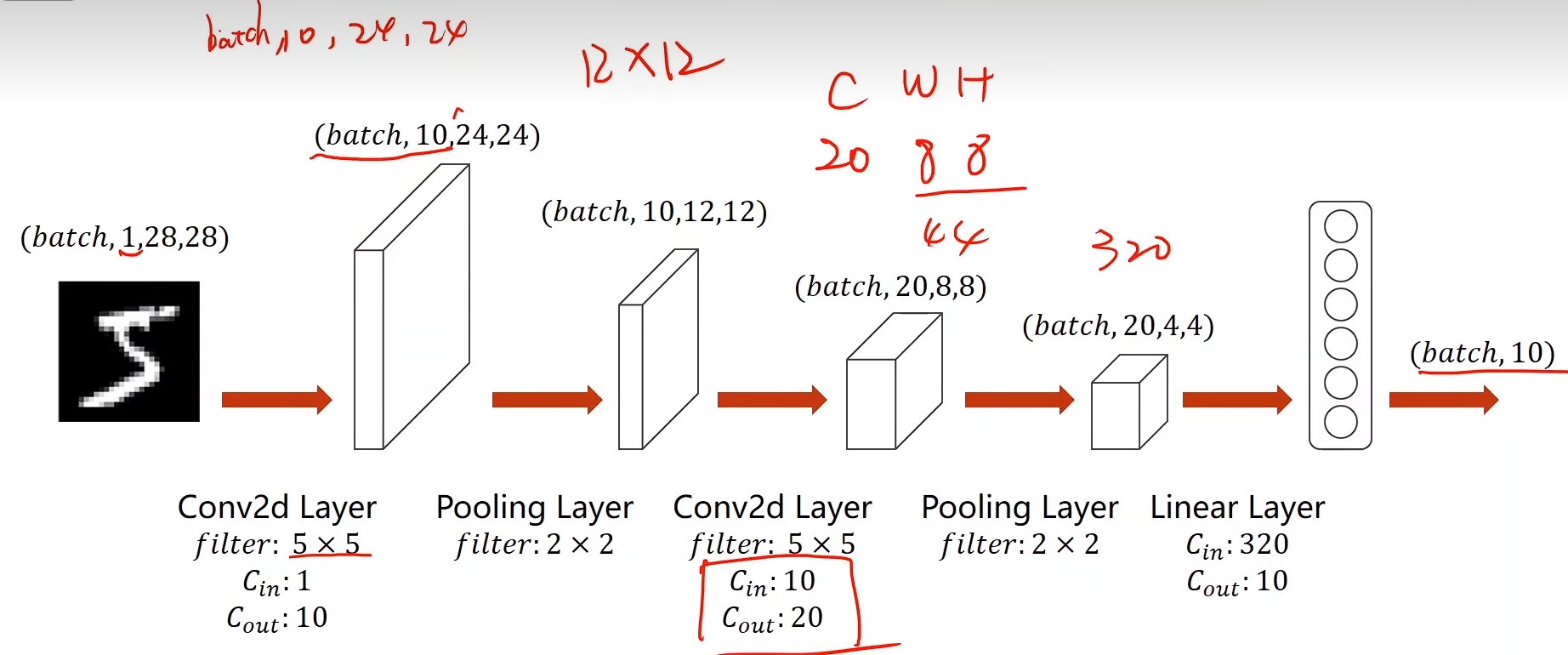
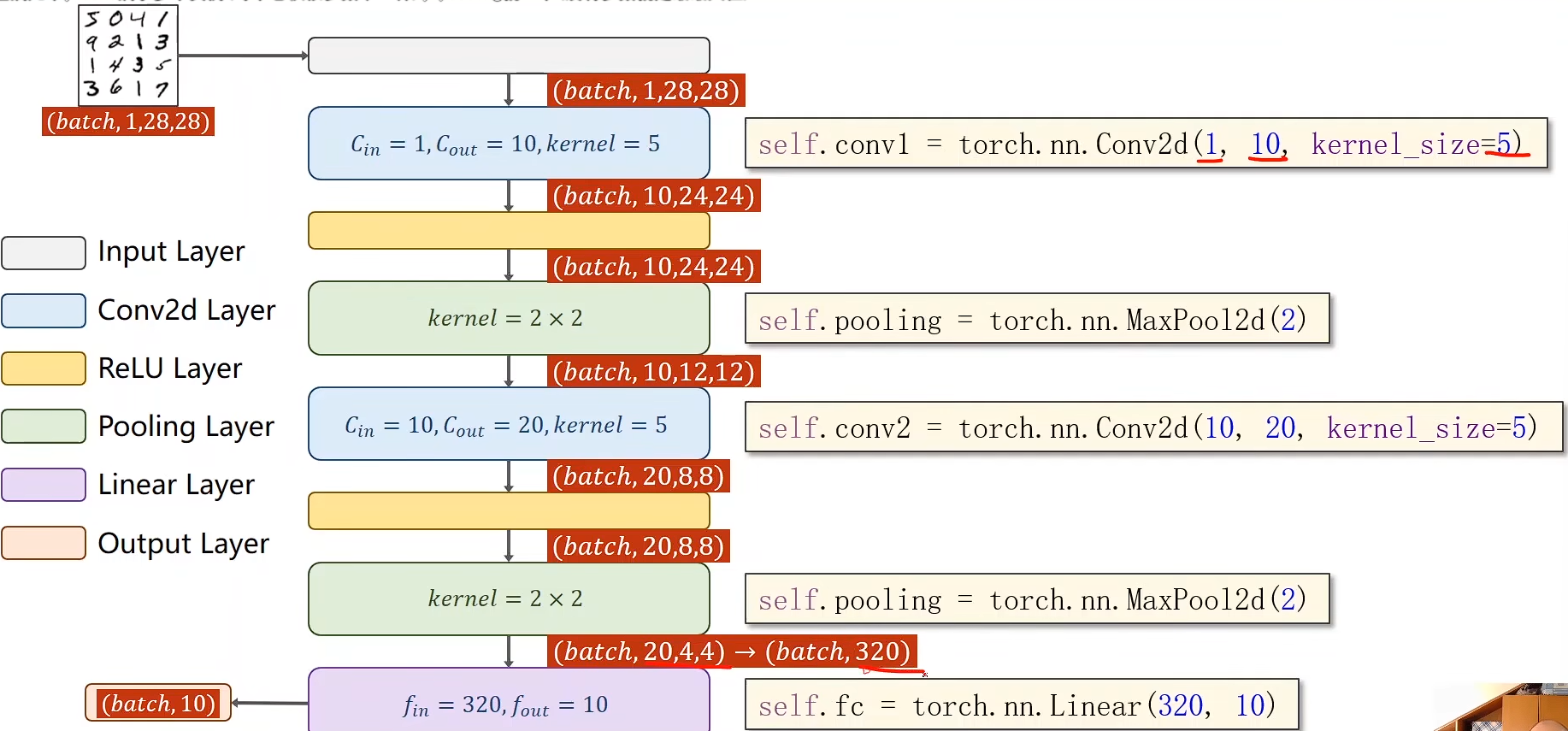
如何在GPU上跑
model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)# 在训练\测试中
inputs, target = inputs.to(device), target.to(device)
mnist_CNN
import torch
import torch.nn.functional as F
import numpy
import torch.optim as optim #关于构建关键优化器
from torch.utils.data import DataLoader, Dataset
from torchvision import transforms
from torchvision import datasets
class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)self.pooling = torch.nn.MaxPool2d(2)self.fc = torch.nn.Linear(320, 10)def forward(self, x):# Flatten data from (n, 1, 28, 28) to (n, 784)batch_size = x.size(0)x = self.pooling(F.relu(self.conv1(x)))x = self.pooling(F.relu(self.conv2(x)))x = x.view(batch_size, -1)x = self.fc(x)return xmodel = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
model.to(device)
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(), #将 PIL图像转换成张量 Tensortransforms.Normalize((0.1307, ), (0.3081, )) #单通道灰度图片# 核心作用是对张量(通常是图像张量)进行标准化(或称归一化)
])
train_dataset = datasets.MNIST(root='./dataset/mnist/',train=True,download=True,transform=transform)
train_loader = DataLoader(train_dataset,batch_size=batch_size,shuffle=True)
test_dataset = datasets.MNIST(root='./dataset/mnist/',train=False,download=True,transform=transform)
test_loader = DataLoader(test_dataset,shuffle=False,batch_size=batch_size)
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
#引入动量 带动量的随机梯度下降(SGD with Momentum)
def train(epoch):running_loss = 0.0for batch_idx, data in enumerate(train_loader, 0):inputs, target = datainputs, target = inputs.to(device), target.to(device)optimizer.zero_grad()output = model(inputs)loss = criterion(output, target)loss.backward()optimizer.step()running_loss += loss.item()if batch_idx % 300 == 299:print('[%d, %5d] loss: %.3f' %(epoch+1, batch_idx + 1, running_loss / 300))running_loss = 0.0def test():correct = 0total = 0with torch.no_grad():for data in test_loader:images, labels = dataimages, labels = images.to(device), labels.to(device)outputs = model(images)_, predicted = torch.max(outputs, dim = 1)total += labels.size(0)correct += (predicted == labels).sum().item()print('Accuracy on test set: %d %%' % (100 * correct / total))if __name__=='__main__':for epoch in range(10):train(epoch)test()
CNN(高级篇)
GoogLeNet
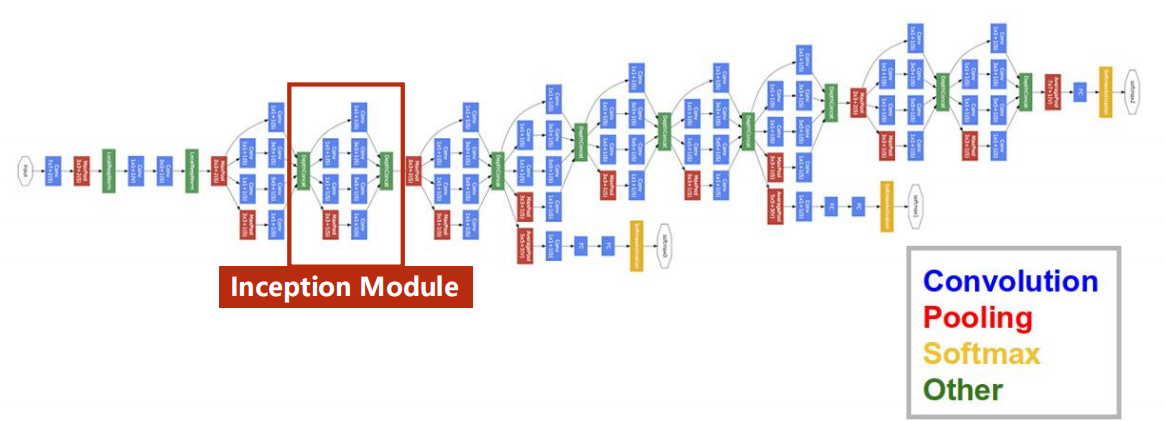
Inception Module
提供候选
Inception Module的核心思想是:在同一个层级上使用多种不同尺寸的卷积核,让网络自动学习选择最合适的特征尺度。
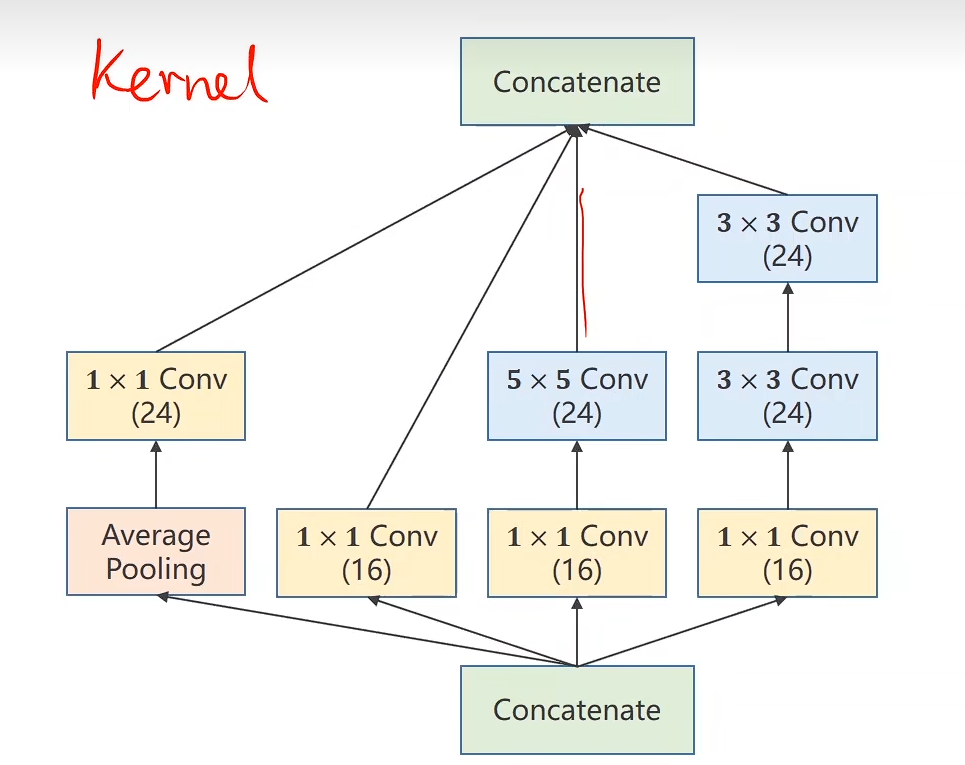
Concatenate:
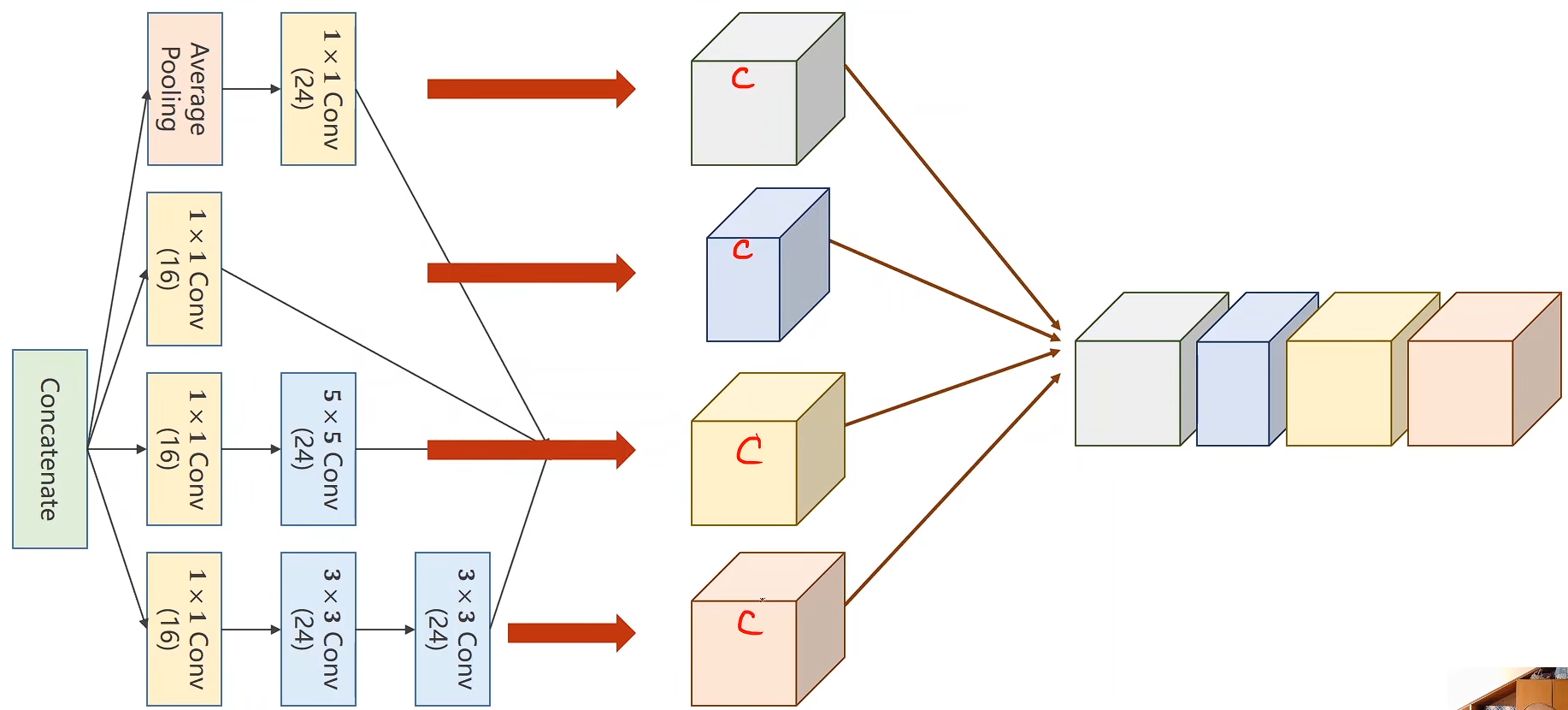
cat
在这里 outputs张量 [B, in_channels, H, W] [batch_size, 输入通道数, 高度, 宽度]
torch.cat(outputs, dim=1)
torch.cat() 用于沿指定维度拼接多个张量。
torch.cat(tensors, dim=0, *, out=None) → Tensor
-
tensors: 要拼接的张量序列(list或tuple)
-
dim: 沿哪个维度进行拼接
-
out: 可选的输出张量
CODE
import torch
import torch.nn.functional as F
class InceptionA(torch.nn.Module):def __init__(self, in_channels):super(InceptionA, self).__init__()#1self.branch1x1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)#2self.branch5x5_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)self.branch5x5_2 = torch.nn.Conv2d(16, 24, kernel_size=5, padding=2)#3self.branch3x3_1 = torch.nn.Conv2d(in_channels, 16, kernel_size=1)self.branch3x3_2 = torch.nn.Conv2d(16, 24, kernel_size=3, padding=1)self.branch3x3_3 = torch.nn.Conv2d(24, 24, kernel_size=3, padding=1)#4self.branch_pool = torch.nn.Conv2d(in_channels, 24, kernel_size=1)def forward(self, x):#1branch1x1 = self.branch1x1(x)#2branch5x5 = self.branch5x5_1(x)branch5x5 = self.branch5x5_2(branch5x5)#3branch3x3 = self.branch3x3_1(x)branch3x3 = self.branch3x3_2(branch3x3)branch3x3 = self.branch3x3_3(branch3x3)#4branch_pool = F.avg_pool2d(x, kernel_size=3, stride=1, padding=1)'''输出高度 = (输入高度 + 2×padding - kernel_size) / stride + 1输出宽度 = (输入宽度 + 2×padding - kernel_size) / stride + 1'''branch_pool = self.branch_pool(branch_pool)#catoutputs = [branch1x1, branch5x5, branch3x3, branch_pool]return torch.cat(outputs, dim=1)class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)self.conv2 = torch.nn.Conv2d(88, 20, kernel_size=5)self.incep1 = InceptionA(in_channels=10)self.incep2 = InceptionA(in_channels=20)self.mp = torch.nn.MaxPool2d(2)self.fc = torch.nn.Linear(1408, 10)def forward(self, x):in_size = x.size(0)x = F.relu(self.mp(self.conv1(x)))x = self.incep1(x)x = F.relu(self.mp(self.conv2(x)))x = self.incep2(x)x = x.view(in_size, -1)x = self.fc(x)return x
Deep Residual Learning 深度残差学习
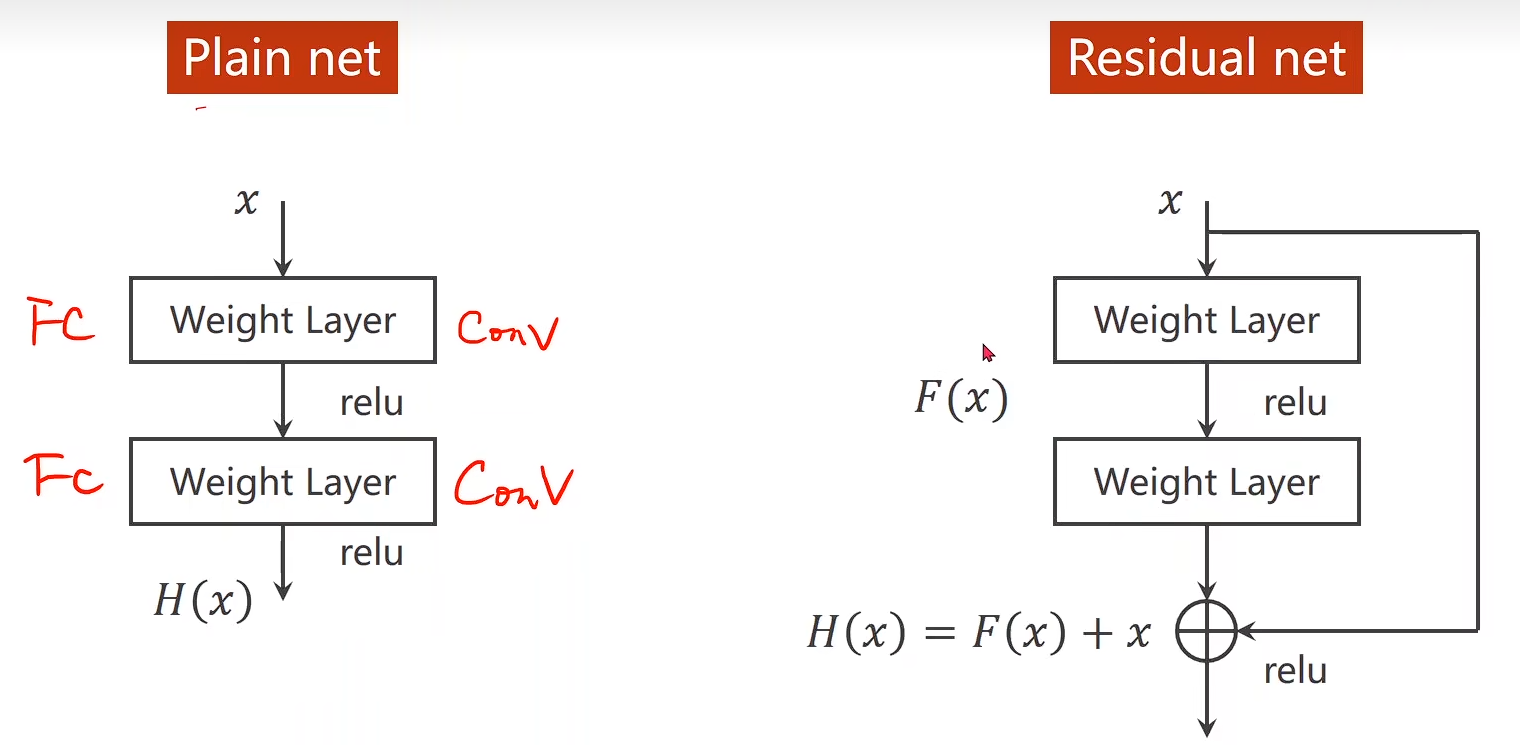
用来解决梯度消失问题
H(x)=F(x)+xH(x) = F(x) + xH(x)=F(x)+x
这个要满足一个前提:输出张量维度 = 输入张量维度
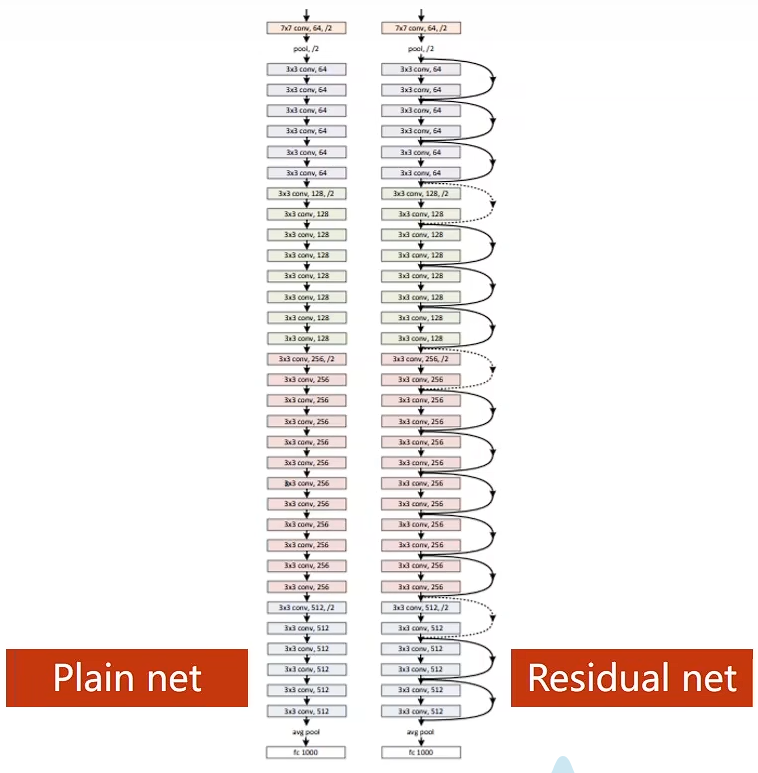
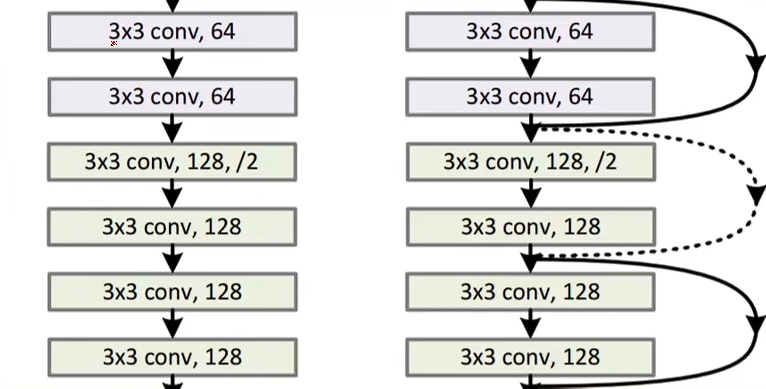
图中虚线是指: 输入张量维度不等于输出张量维度,这个地方要单独处理
- 直接不跳连接
- 将 x 进行最大池化操作
- 其他
EG
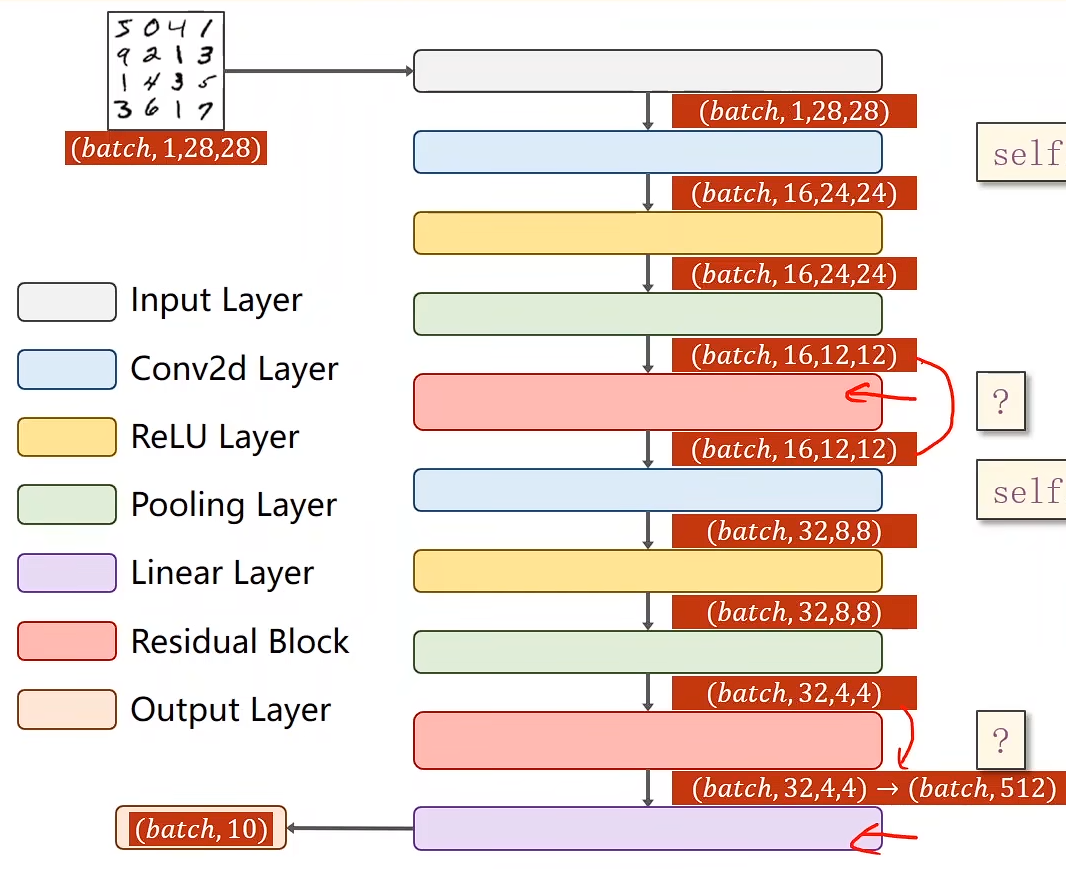
import torch
import torch.nn.functional as Fclass ResidualBlock(torch.nn.Module):def __init__(self, channels):super(ResidualBlock, self).__init__()self.channels = channelsself.conv1 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)self.conv2 = torch.nn.Conv2d(channels, channels, kernel_size=3, padding=1)def forward(self, x):y = F.relu(self.conv1(x))y = self.conv2(y)return F.relu(x + y)class Net(torch.nn.Module):def __init__(self):super(Net, self).__init__()self.conv1 = torch.nn.Conv2d(1, 16, kernel_size=5)self.conv2 = torch.nn.Conv2d(16, 32, kernel_size=5)self.mp = torch.nn.MaxPool2d(2)self.rblock1 = ResidualBlock(16)self.rblock2 = ResidualBlock(32)self.fc = torch.nn.Linear(512, 10)def forward(self, x):in_size = x.size(0)x = self.mp(F.relu(self.conv1(x)))x = self.rblock1(x)x = self.mp(F.relu((self.conv2(x))))x = self.view(in_size, -1)x = self.fc(x)return x
可以阅读文献以来扩展
-
He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks[C]
-
Huang G, Liu Z, Laurens V D M, et al. Densely Connected Convolutional NetworksIJl. 2016:2261-2269.
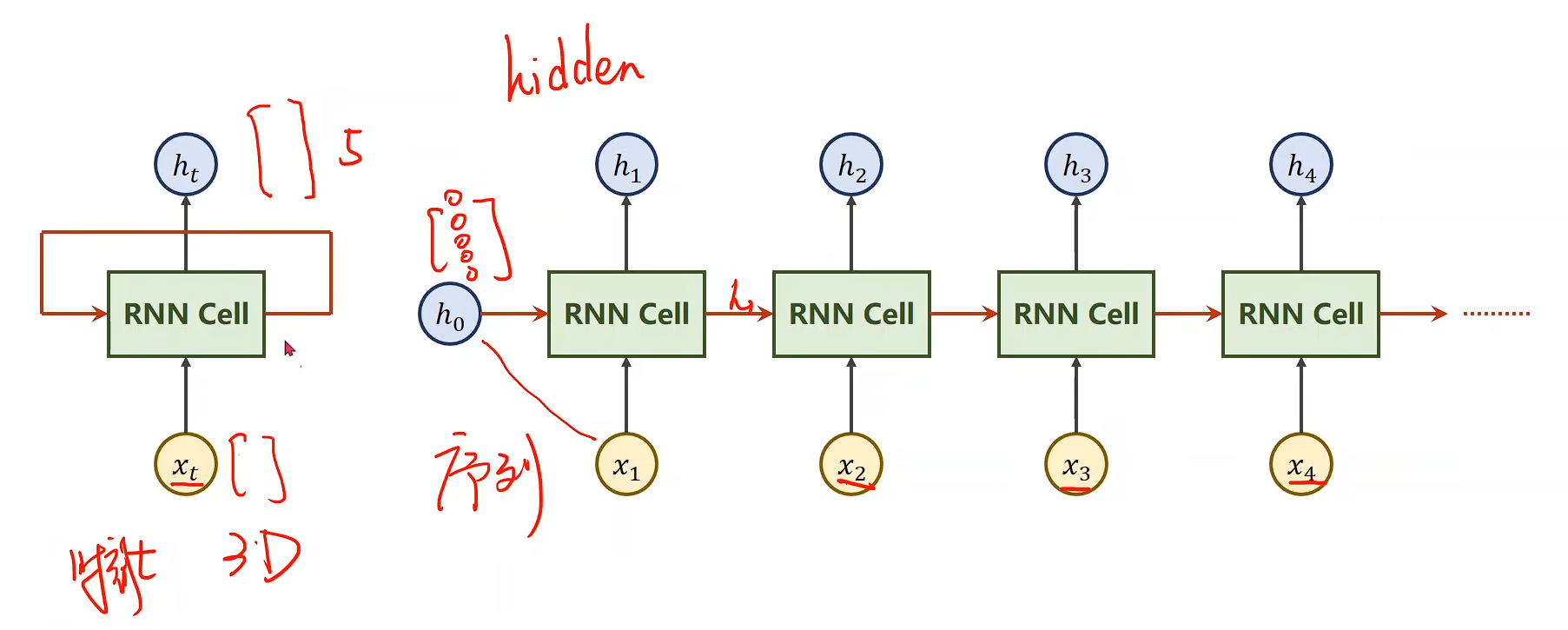
循环神经网络RNN(基础篇)
1.基本概念
RNN 是一种 处理序列数据 的神经网络模型。它的最大特点是:
- 引入循环结构:当前时刻的输出不仅依赖于当前输入,还依赖于上一个时刻的隐藏状态。
- 这样网络就能“记住”一定的历史信息,适合处理 时间序列 或 上下文相关 的任务。
公式可以简单表示为:
ht=f(Wxhxt+Whhht−1+bh)h_t = f(W_{xh} x_t + W_{hh} h_{t-1} + b_h) ht=f(Wxhxt+Whhht−1+bh)
其中:
- xtx_txt:当前输入
- hth_tht:当前隐藏状态
- ht−1h_{t-1}ht−1:前一时刻隐藏状态
- yty_tyt:输出
2. 应用场景
RNN 特别适合处理顺序相关的任务:
- 自然语言处理:机器翻译、文本生成、语音识别
- 时间序列预测:股票预测、传感器数据分析
- 序列标注任务:词性标注、命名实体识别
3. 局限性
- 梯度消失/爆炸:在长序列训练时,RNN 难以捕捉长距离依赖。
- 并行性差:计算依赖前一时刻,训练效率低。
4. 改进模型
为了解决上述问题,出现了很多改进版本:
- LSTM(Long Short-Term Memory):引入门控机制,能记忆更长的序列。
- GRU(Gated Recurrent Unit):简化版的 LSTM,效果接近但结构更简单。
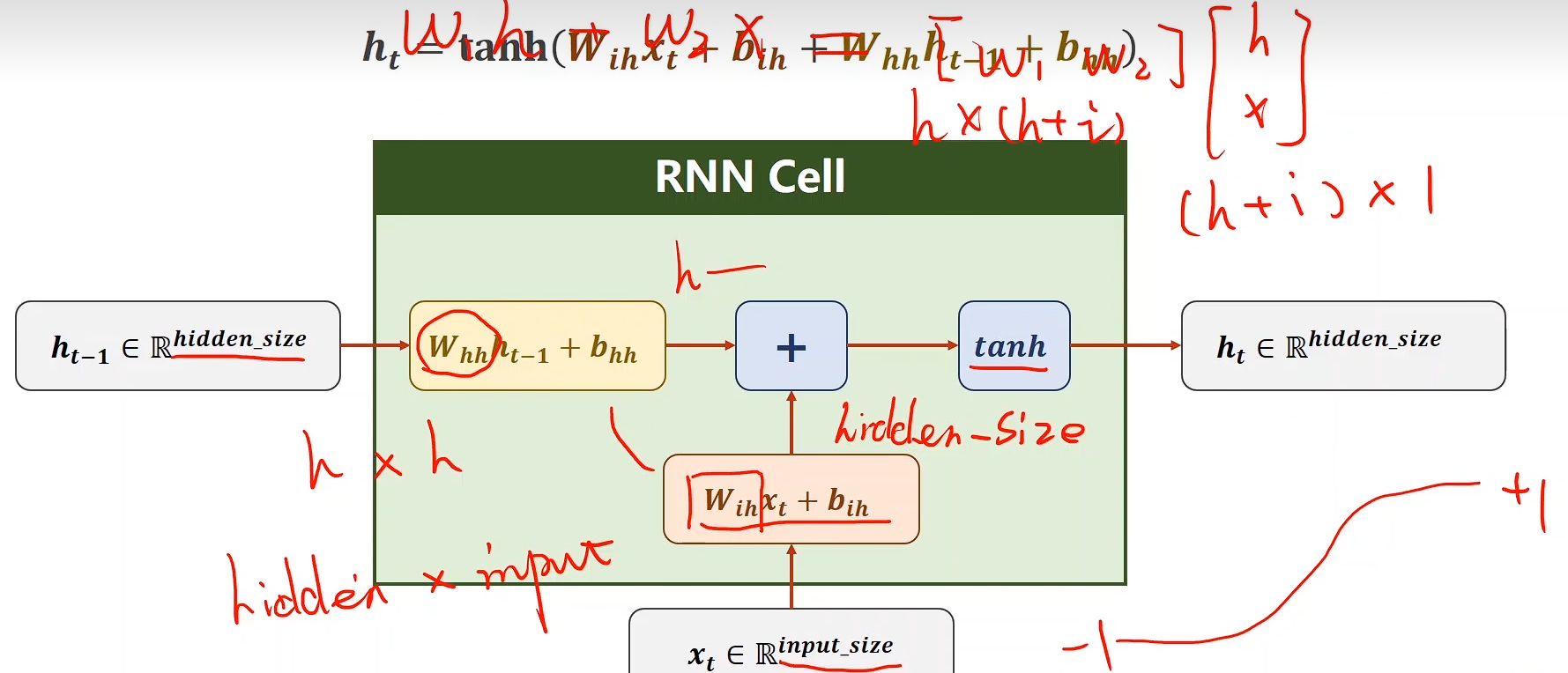
如何实现
自己设置 RNN Cell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)
需要两个值:
- 输入的维度
- 隐层的维度
有了这两个值就可以把权重的维度和偏置的维度确定下来
本质上还是一个线形层
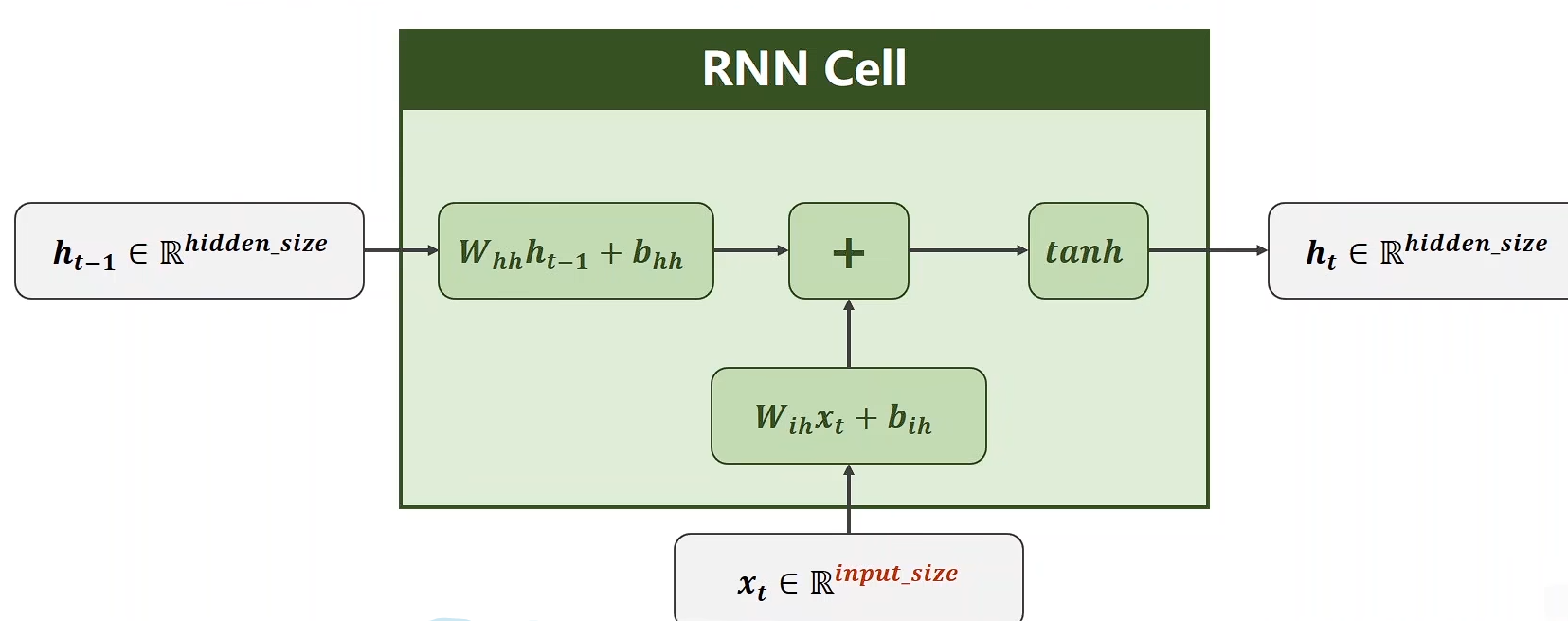
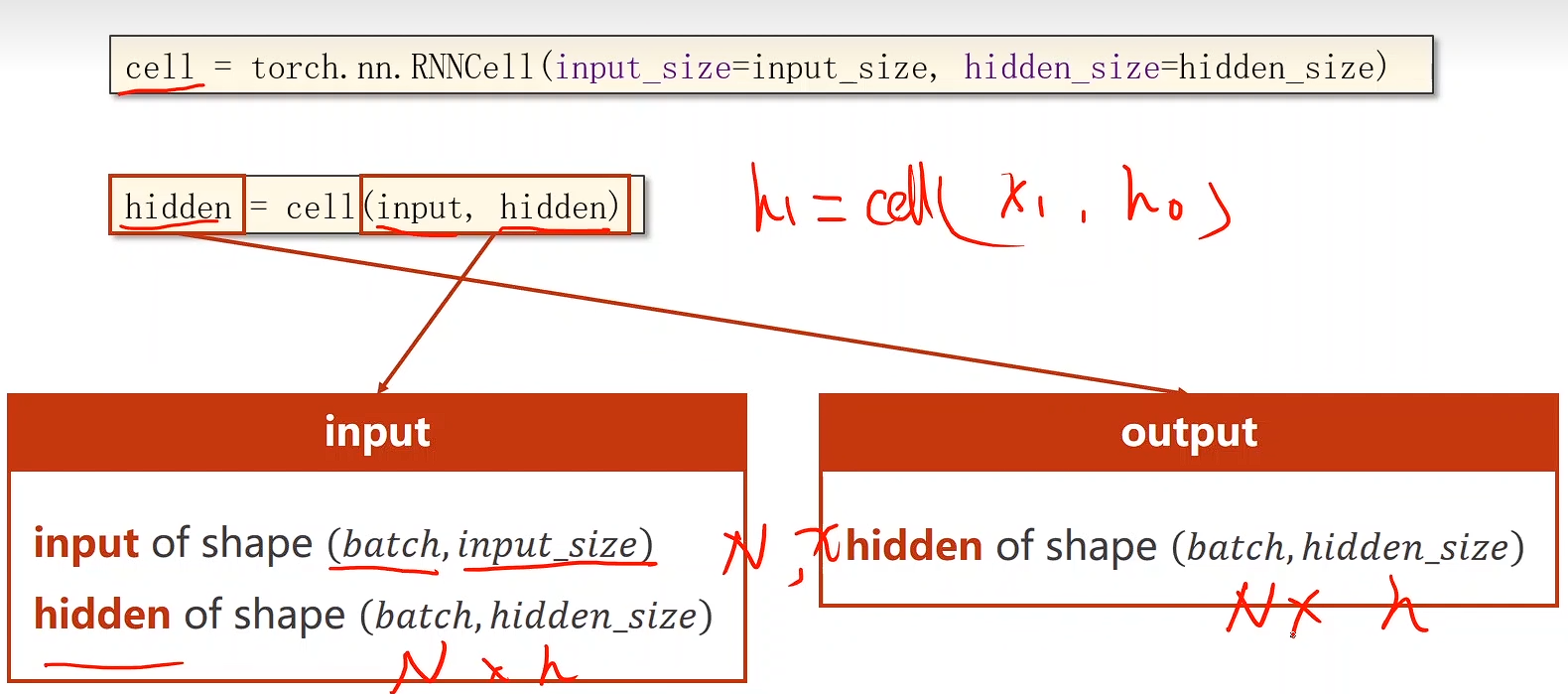
Eg:
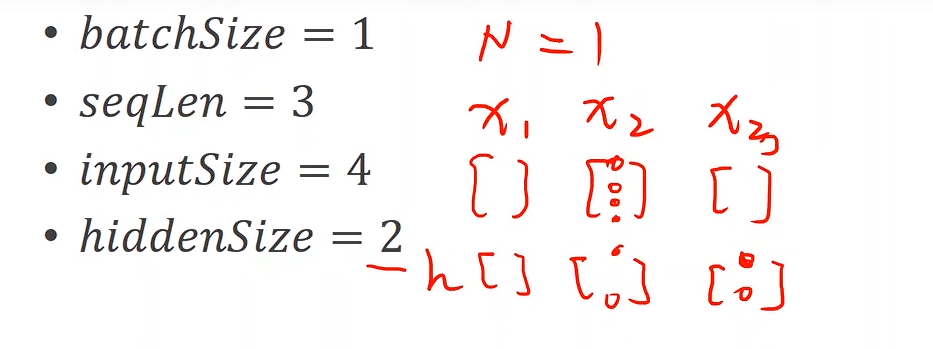


import torch# Set Parameters
batch_size = 1
seq_len = 3
input_size = 4
hidden_size = 2# Construction of RNNCell
cell = torch.nn.RNNCell(input_size=input_size, hidden_size=hidden_size)# (seq, batch, features)
dataset = torch.randn(seq_len, batch_size, input_size)
hidden = torch.zeros(batch_size, hidden_size) #Initializing the hidden to zerofor idx, input in enumerate(dataset):print('=' * 20, idx, '=' * 20)print('Input size:', input.shape)hidden = cell(input, hidden)print('hidden size', hidden.shape)print(hidden)torch.randn(...)
- 生成一个张量(tensor),元素来自 标准正态分布 N(0,1)(均值为 0,方差为 1)。
- 每次运行会得到不同的随机数。
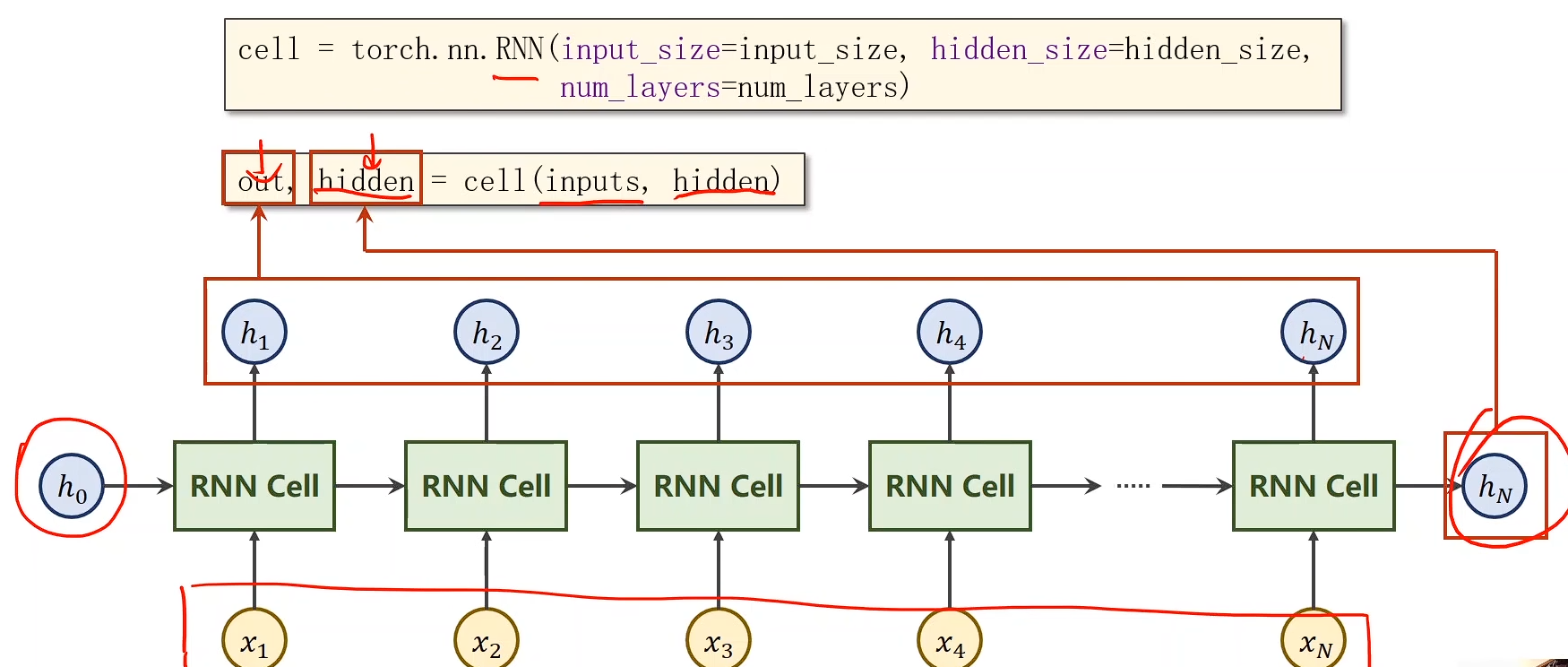
使用RNN
cell = torch.nn.RNN(input_size=input_size, hidden_size= = hidden_size, num_layers = num_layers)

- Suppose we have sequence with below properties:
- batchSize
- seqLen
- inputSize, hiddenSize
- numLayers
- The shape of input and h₀ of RNN:
input.shape = (seqLen, batchSize, inputSize)h₀.shape = (numLayers, batchSize, hiddenSize)
- The shape of output and hₙ of RNN:
output.shape = (seqLen, batchSize, hiddenSize)hₙ.shape = (numLayers, batchSize, hiddenSize)
RNN - numLayers
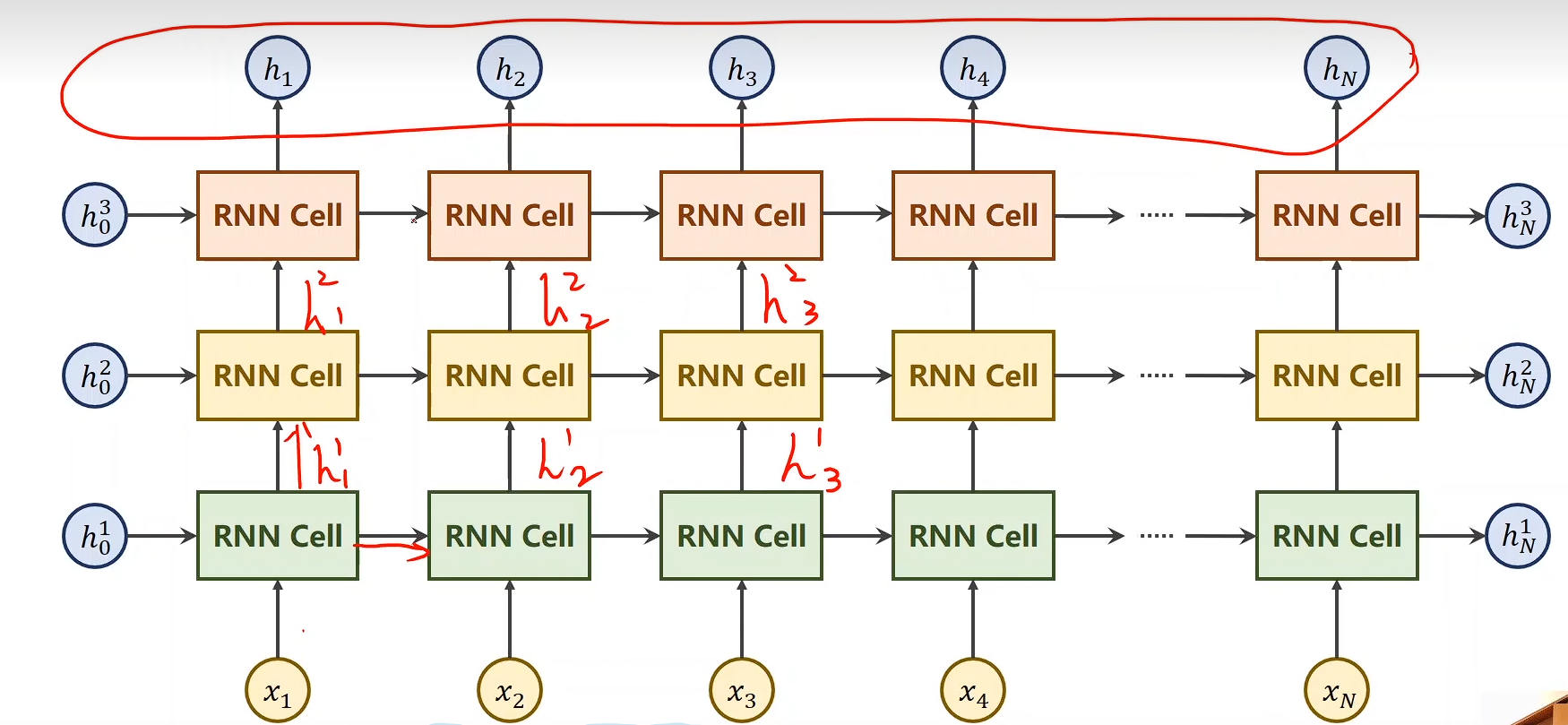
import torchbatch_size = 1
seq_len= 3
input_size = 4
hidden_size = 2
num_layers = 1cell = torch.nn.RNN(input_size=input_size, hidden_size=hidden_size, num_layers=num_layers)# (seqLen, batchSize, inputSize)
inputs = torch.randn(seq_len, batch_size, input_size)
hidden = torch.zeros(num_layers, batch_size, hidden_size)out, hidden = cell(inputs, hidden)print('Output size:', out.shape)
print('Output', out)
print('Hidden size:', hidden.shape)
print('Hidden:', hidden)
batch_first
有时候这样操作后更好构造

Eg:
Train a model to learn:
$ hello\ \to \ ohlol$
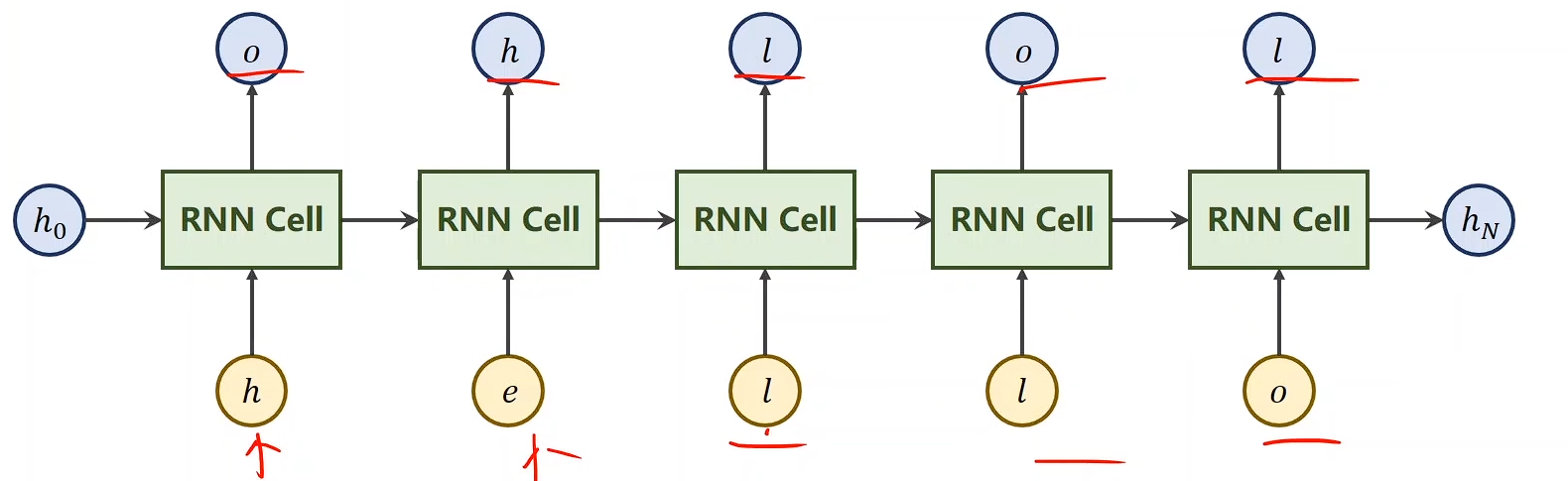
RNN 单元的输入应该是数字向量:
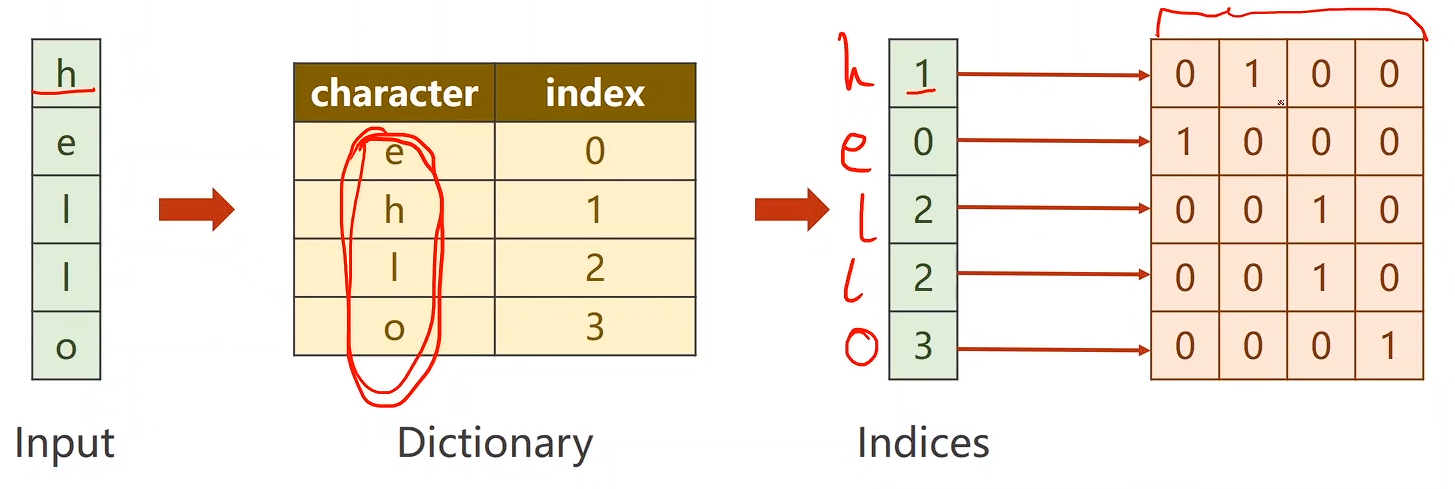
InputSize = 4
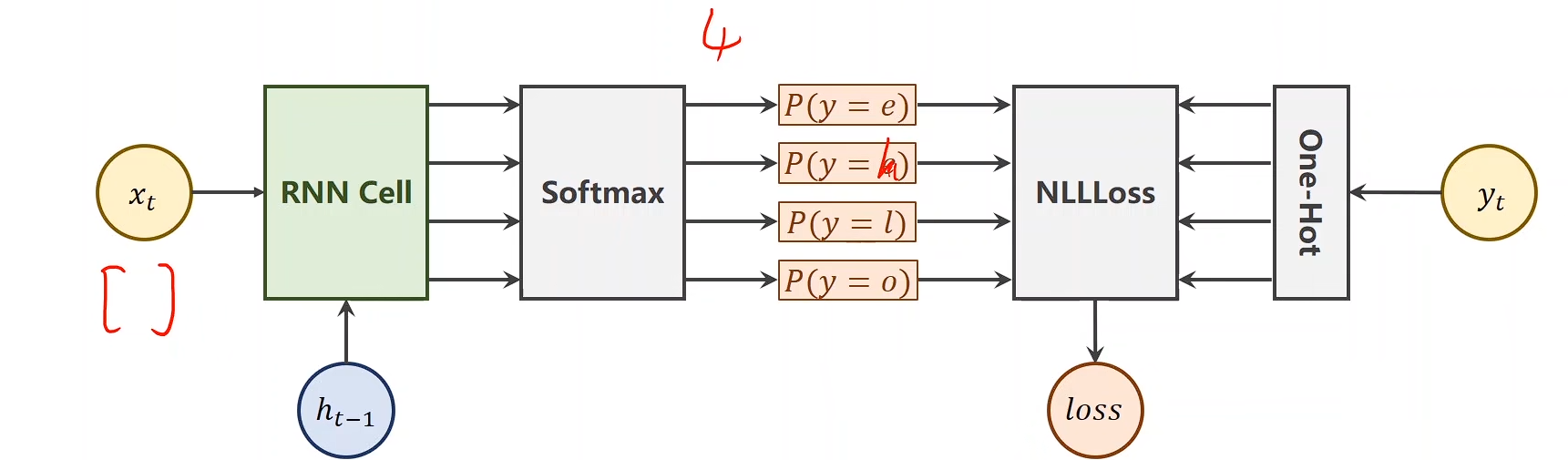
RNN单元的输出应为预测向量
OutputSize = 4
RNN_Cell方法:
import torchinput_size = 4
hidden_size = 4
batch_size = 1
# Prepare data
idx2char = ['e', 'h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [3, 1, 2, 3, 2]one_hot_lookup = [[1, 0, 0, 0],[0, 1, 0, 0],[0, 0, 1, 0],[0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]inputs = torch.Tensor(x_one_hot).view(-1, batch_size, input_size)
labels = torch.LongTensor(y_data).view(-1, 1)class Model(torch.nn.Module):def __init__(self, input_size, hidden_size, batch_size):super(Model, self).__init__()# self.num_layers = num_layersself.batch_size = batch_sizeself.input_size = input_sizeself.hidden_size = hidden_sizeself.rnncell = torch.nn.RNNCell(input_size = self.input_size,hidden_size=hidden_size)def forward(self, input, hidden):hidden = self.rnncell(input, hidden)return hiddendef init_hidden(self):return torch.zeros(self.batch_size, self.hidden_size)net = Model(input_size, hidden_size, batch_size)criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.1)for epoch in range(20):loss = 0optimizer.zero_grad()hidden = net.init_hidden()print('Predicted string:', end = '')for input, label in zip(inputs, labels):hidden = net(input, hidden)loss += criterion(hidden, label)_, idx = hidden.max(dim = 1)print(idx2char[idx.item()], end='')loss.backward()optimizer.step()print(', Epoch [%5d/20] loss=%.4f' % (epoch + 1, loss.item()))使用RNN方法
import torchinput_size = 4
hidden_size = 4
batch_size = 1
num_layers = 1
seq_len = 5
# Prepare data
idx2char = ['e', 'h', 'l', 'o']
x_data = [1, 0, 2, 2, 3]
y_data = [3, 1, 2, 3, 2]one_hot_lookup = [[1, 0, 0, 0],[0, 1, 0, 0],[0, 0, 1, 0],[0, 0, 0, 1]]
x_one_hot = [one_hot_lookup[x] for x in x_data]inputs = torch.Tensor(x_one_hot).view(seq_len, batch_size, input_size)
labels = torch.LongTensor(y_data)class Model(torch.nn.Module):def __init__(self, input_size, hidden_size, batch_size, num_layers=1):super(Model, self).__init__()self.num_layers = num_layersself.batch_size = batch_sizeself.input_size = input_sizeself.hidden_size = hidden_sizeself.rnn = torch.nn.RNN(input_size = self.input_size,hidden_size=hidden_size,num_layers = num_layers)def forward(self, input):hidden = torch.zeros(self.num_layers,self.batch_size,self.hidden_size)out, _ = self.rnn(input, hidden)return out.view(-1, self.hidden_size)net = Model(input_size, hidden_size, batch_size, num_layers)criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.1)for epoch in range(100):optimizer.zero_grad()outputs = net(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()_, idx = outputs.max(dim = 1)idx = idx.data.numpy()print('Predicted:', ''.join(idx2char[x] for x in idx), end='')print(', Epoch [%5d/100] loss=%.4f' % (epoch + 1, loss.item()))
EMBEDDING
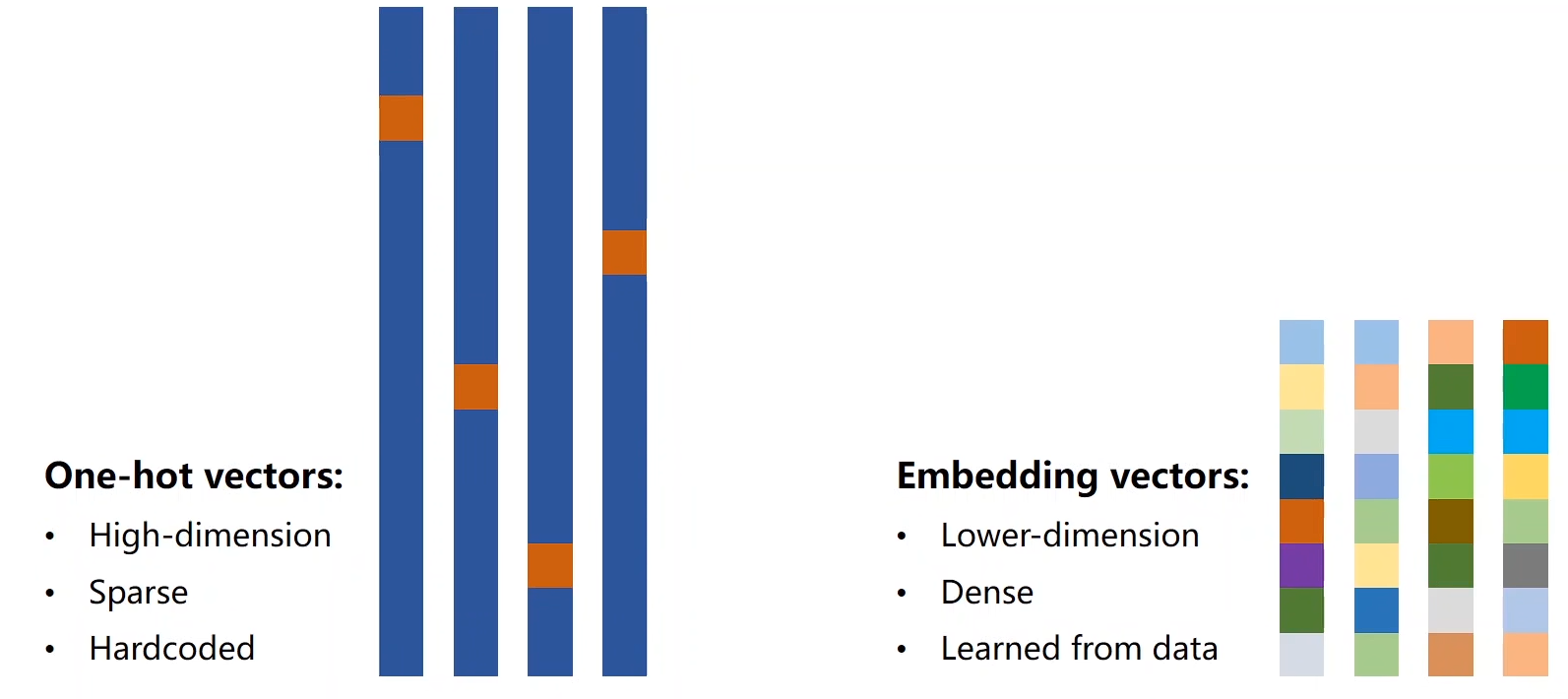
将高维稀疏的样本 映射到 稠密低维的 (常说的数据降维,当然这个操作可以降维也可以升维)
import torchnum_class = 4
input_size = 4
hidden_size = 8
embedding_size = 10
num_layers = 2
batch_size = 1
seq_len = 5
idx2char = ['e', 'h', 'l', 'o']
x_data = [[1, 0, 2, 2, 3]]
y_data = [3, 1, 2, 3, 2]inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)
class Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.emb = torch.nn.Embedding(input_size, embedding_size)self.rnn = torch.nn.RNN(input_size=embedding_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True)self.fc = torch.nn.Linear(hidden_size, num_class)def forward(self, x):hidden = torch.zeros(num_layers, x.size(0), hidden_size)x = self.emb(x)x, _ = self.rnn(x, hidden)x = self.fc(x)return x.view(-1, num_class)net = Model()criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)for epoch in range(20):optimizer.zero_grad()outputs = net(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()_, idx = outputs.max(dim=1)idx = idx.data.numpy()print('Predicted:', ''.join(idx2char[x] for x in idx), end='')print(', Epoch [%5d/20] loss=%.4f' % (epoch + 1, loss.item()))
LSTM
1. LSTM 的基本概念
LSTM(Long Short-Term Memory)是一种特殊的循环神经网络(RNN),专门设计用来解决传统RNN的梯度消失/爆炸问题,能够学习长期依赖关系。
2. LSTM 的核心结构
LSTM 的关键在于其门控机制,包含三个门:
三个门控结构:
import torch
import torch.nn as nn# LSTM 单元的基本运算
class LSTMCell(nn.Module):def __init__(self, input_size, hidden_size):super().__init__()# 输入门、遗忘门、输出门、候选细胞状态self.linear = nn.Linear(input_size + hidden_size, 4 * hidden_size)def forward(self, x, h, c):# x: 当前输入, h: 隐藏状态, c: 细胞状态combined = torch.cat([x, h], dim=1)gates = self.linear(combined)# 分割为四个部分i, f, g, o = gates.chunk(4, 1)# 激活函数i = torch.sigmoid(i) # 输入门f = torch.sigmoid(f) # 遗忘门g = torch.tanh(g) # 候选值o = torch.sigmoid(o) # 输出门# 更新细胞状态c_new = f * c + i * g# 更新隐藏状态h_new = o * torch.tanh(c_new)return h_new, c_new
3. LSTM 的三个门详解
遗忘门(Forget Gate)
决定从细胞状态中丢弃什么信息
f_t = σ(W_f · [h_{t-1}, x_t] + b_f)
输入门(Input Gate)
决定什么新信息被存储到细胞状态中
i_t = σ(W_i · [h_{t-1}, x_t] + b_i)
g_t = tanh(W_g · [h_{t-1}, x_t] + b_g)
输出门(Output Gate)
基于细胞状态决定输出什么信息
o_t = σ(W_o · [h_{t-1}, x_t] + b_o)
h_t = o_t * tanh(c_t)
4. PyTorch 中的 LSTM 使用
基本用法:
import torch.nn as nn# 定义 LSTM
lstm = nn.LSTM(input_size=100, # 输入特征维度hidden_size=128, # 隐藏层维度num_layers=2, # LSTM 层数batch_first=True, # 输入形状为 (batch, seq, feature)dropout=0.2, # 层间dropoutbidirectional=False # 是否双向
)# 前向传播
input_data = torch.randn(32, 10, 100) # (batch, seq_len, input_size)
h0 = torch.zeros(2, 32, 128) # (num_layers, batch, hidden_size)
c0 = torch.zeros(2, 32, 128) # (num_layers, batch, hidden_size)output, (hn, cn) = lstm(input_data, (h0, c0))
print(f"Output shape: {output.shape}") # (32, 10, 128)
print(f"Hidden state shape: {hn.shape}") # (2, 32, 128)
Eg:
import torchnum_class = 4
input_size = 4
hidden_size = 8
embedding_size = 10
num_layers = 2
batch_size = 1
seq_len = 5
idx2char = ['e', 'h', 'l', 'o']
x_data = [[1, 0, 2, 2, 3]]
y_data = [3, 1, 2, 3, 2]inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)class Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.emb = torch.nn.Embedding(input_size, embedding_size)self.lsrm = torch.nn.LSTM(input_size=embedding_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True)self.fc = torch.nn.Linear(hidden_size, num_class)def forward(self, x):hidden = torch.zeros(num_layers, x.size(0), hidden_size)x = self.emb(x)x, _ =self.lsrm(x)x = self.fc(x)return x.view(-1, num_class)net = Model()criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)for epoch in range(20):optimizer.zero_grad()outputs = net(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()_, idx = outputs.max(dim=1)idx = idx.data.numpy()print('Predicted:', ''.join(idx2char[x] for x in idx), end='')print(', Epoch [%5d/20] loss=%.4f' % (epoch + 1, loss.item()))5. LSTM 的优势
相比传统RNN的优势:
- 解决梯度消失:通过门控机制和细胞状态
- 长期记忆:可以记住数百个时间步之前的信息
- 选择性记忆:自动学习记住重要信息,忘记不重要信息
应用场景:
- 自然语言处理:机器翻译、文本生成、情感分析
- 时间序列预测:股票价格、天气预测
- 语音识别:音频序列处理
- 视频分析:动作识别
GRU
重置门(Reset Gate)
决定如何将新的输入与之前的记忆结合
r_t = σ(W_r · [h_{t-1}, x_t] + b_r)
更新门(Update Gate)
决定多少之前的信息传递到当前状态
z_t = σ(W_z · [h_{t-1}, x_t] + b_z)
候选隐藏状态
h̃_t = tanh(W · [r_t * h_{t-1}, x_t] + b)
最终隐藏状态
h_t = z_t * h_{t-1} + (1 - z_t) * h̃_t
4. PyTorch 中的 GRU 使用
基本用法:
import torch.nn as nn# 定义 GRU
gru = nn.GRU(input_size=100, # 输入特征维度hidden_size=128, # 隐藏层维度num_layers=2, # GRU 层数batch_first=True, # 输入形状为 (batch, seq, feature)dropout=0.2, # 层间dropoutbidirectional=False # 是否双向
)# 前向传播
input_data = torch.randn(32, 10, 100) # (batch, seq_len, input_size)
h0 = torch.zeros(2, 32, 128) # (num_layers, batch, hidden_size)output, hn = gru(input_data, h0)
print(f"Output shape: {output.shape}") # (32, 10, 128)
print(f"Hidden state shape: {hn.shape}") # (2, 32, 128)
Eg:
import torchnum_class = 4
input_size = 4
hidden_size = 8
embedding_size = 10
num_layers = 2
batch_size = 1
seq_len = 5
idx2char = ['e', 'h', 'l', 'o']
x_data = [[1, 0, 2, 2, 3]]
y_data = [3, 1, 2, 3, 2]inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)class Model(torch.nn.Module):def __init__(self):super(Model, self).__init__()self.emb = torch.nn.Embedding(input_size, embedding_size)self.gru = torch.nn.GRU(input_size=embedding_size,hidden_size=hidden_size,num_layers=num_layers,batch_first=True)self.fc = torch.nn.Linear(hidden_size, num_class)def forward(self, x):hidden = torch.zeros(num_layers, x.size(0), hidden_size)x = self.emb(x)x, _ =self.gru(x)x = self.fc(x)return x.view(-1, num_class)net = Model()criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)for epoch in range(20):optimizer.zero_grad()outputs = net(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()_, idx = outputs.max(dim=1)idx = idx.data.numpy()print('Predicted:', ''.join(idx2char[x] for x in idx), end='')print(', Epoch [%5d/20] loss=%.4f' % (epoch + 1, loss.item()))GRU vs LSTM
结构对比:
| 特性 | GRU | LSTM |
|---|---|---|
| 参数数量 | 较少 | 较多 |
| 训练速度 | 较快 | 较慢 |
| 门控数量 | 2个(重置门、更新门) | 3个(输入门、遗忘门、输出门) |
| 状态数量 | 1个(隐藏状态) | 2个(隐藏状态、细胞状态) |
| 性能 | 在大多数任务上与LSTM相当 | 在某些需要长期记忆的任务上略优 |
相比LSTM的优势:
- 参数更少:少了1个门和细胞状态,计算更高效
- 训练更快:更简单的结构意味着更快的训练速度
- 内存占用更小:只需要维护一个隐藏状态
- 在某些任务上表现更好:特别是小数据集
应用场景:
- 文本生成:比LSTM训练更快
- 机器翻译:在很多翻译模型中替代LSTM
- 语音识别:实时性要求高的场景
- 时间序列预测:需要快速训练的场景
RNN(高级篇)
Name Classification

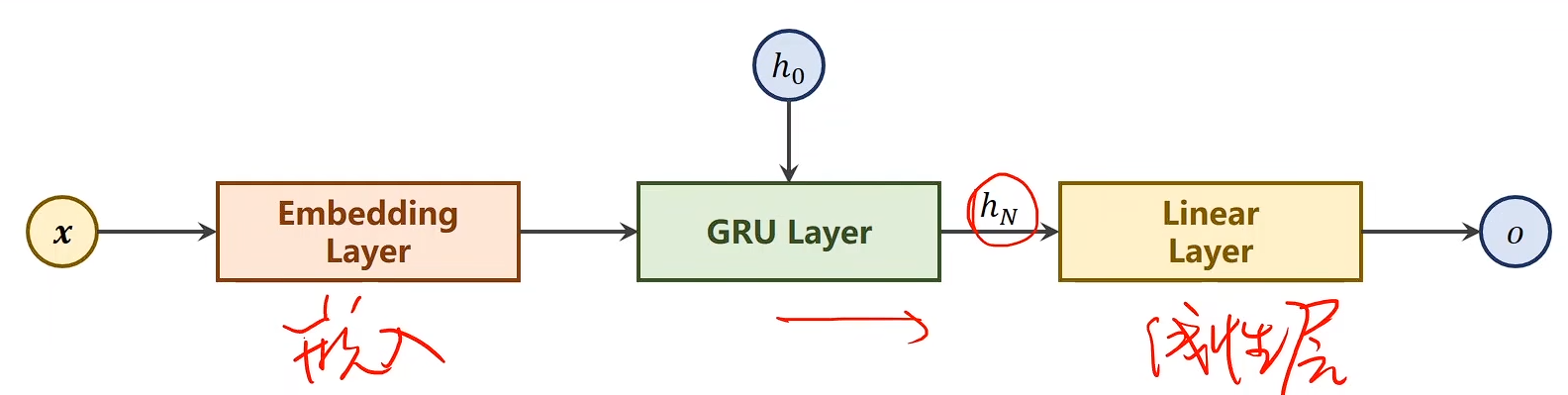
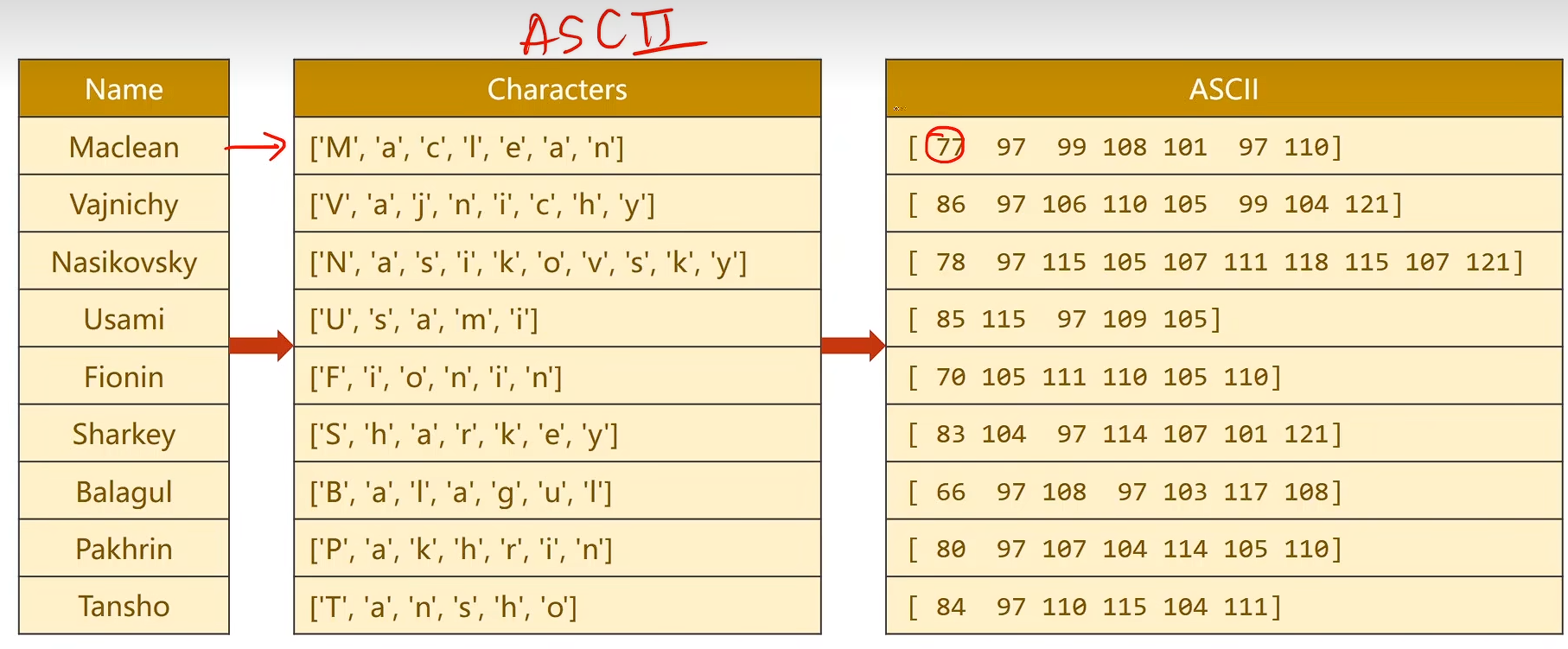
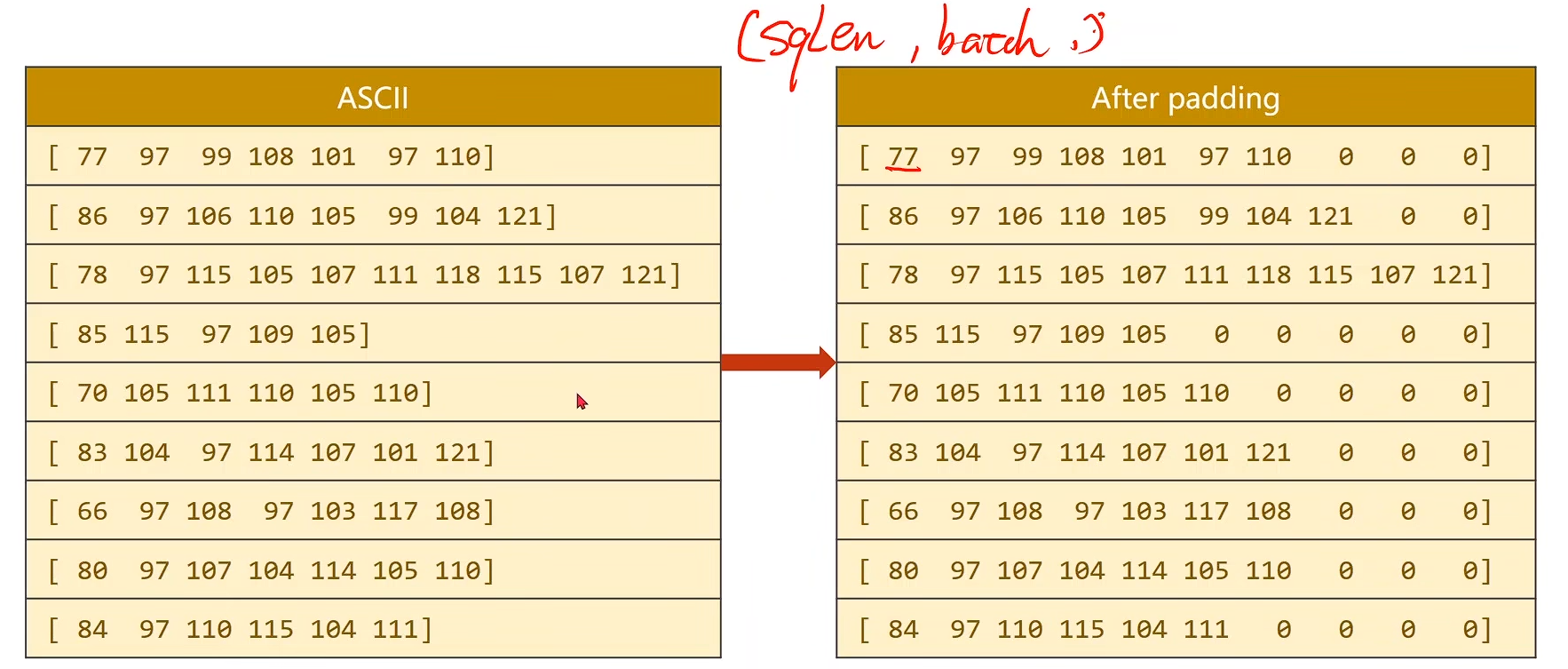
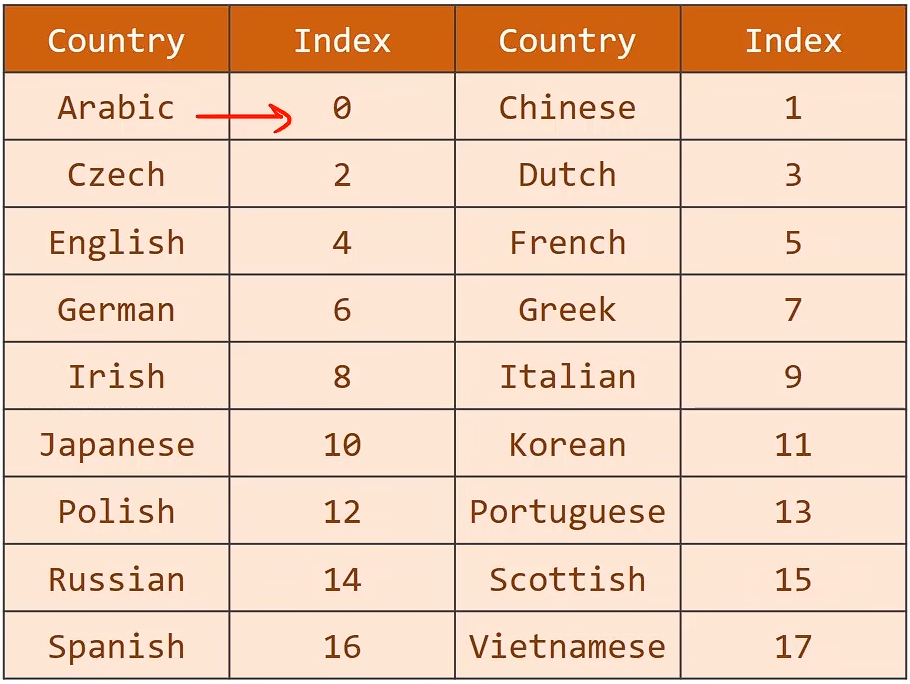
import os
os.environ["KMP_DUPLICATE_LIB_OK"] = "TRUE"
import math
import timeimport matplotlib.pyplot as plt
import numpy as np
import torch
from torch.nn.utils.rnn import pack_padded_sequence
from torch.utils.data import Dataset, DataLoader
import pandas as pdN_CHARS = 128
HIDDEN_SIZE =100
BATCH_SIZE = 256
N_LAYER = 2
N_EPOCHS = 100
USE_GPU = Trueclass NameDataset(Dataset):def __init__(self, is_train_set=True):filename = './dataset/name_classification/names_train.csv' if is_train_set else './dataset/name_classification/names_test.csv'df = pd.read_csv(filename, header=None, names=['name', 'country'])self.names = df['name'].valuesself.len = len(self.names)self.countries = df['country'].valuesself.country_list = list(sorted(set(self.countries)))self.country_dict = self.getCountryDict()self.country_num = len(self.country_list)def __getitem__(self, idx):return self.names[idx], self.country_dict[self.countries[idx]]def __len__(self):return self.lendef getCountryDict(self):country_dict = dict()for idx, country_name in enumerate(self.country_list, 0):country_dict[country_name] = idxreturn country_dictdef idx2country(self, idx):return self.country_list[idx]def getCountriesNum(self):return self.country_numclass RNNClassifier(torch.nn.Module):def __init__(self, input_size, hidden_size, output_size, n_layers=1, bidirectional=True):super(RNNClassifier, self).__init__()self.hidden_size = hidden_sizeself.n_layers = n_layersself.n_directions = 2 if bidirectional else 1self.embedding = torch.nn.Embedding(input_size, hidden_size)self.gru = torch.nn.GRU(hidden_size, hidden_size, n_layers, bidirectional=bidirectional)self.fc = torch.nn.Linear(hidden_size * self.n_directions, output_size)def _init_hidden(self, batch_size):hidden = torch.zeros(self.n_layers * self.n_directions, batch_size, self.hidden_size)return create_tensor(hidden)def forward(self, input, seq_lengths):# input shape: B x S -> S x Binput = input.t()batch_size = input.size(1)hidden = self._init_hidden(batch_size)embedding = self.embedding(input)#pack them upgru_input = pack_padded_sequence(embedding, seq_lengths)output, hidden = self.gru(gru_input, hidden)if self.n_directions == 2:hidden_cat = torch.cat([hidden[-1], hidden[-2]], dim=1)else:hidden_cat = hidden[-1]fc_output = self.fc(hidden_cat)return fc_outputdef time_since(since):s = time.time() - sincem = math.floor(s / 60)s -= m * 60return '%dm %ds' % (m, s)def name2list(name):arr = [ord(c) for c in name]return arr, len(arr)def create_tensor(tensor):if USE_GPU:device = torch.device("cuda:0")tensor = tensor.to(device)return tensordef make_tensors(names, countries):sequences_and_lengths = [name2list(name) for name in names]name_sequences = [sl[0] for sl in sequences_and_lengths]seq_lengths = torch.LongTensor([sl[1] for sl in sequences_and_lengths])countries = countries.long()#make tensor of name, BatchSize x Seqlenseq_tensor = torch.zeros(len(name_sequences), seq_lengths.max().item()).long()for idx, (seq, seq_len) in enumerate(zip(name_sequences, seq_lengths), 0):seq_tensor[idx, :seq_len] = torch.LongTensor(seq)# sort by length to use pack_padded_sequenceseq_lengths, perm_idx = seq_lengths.sort(dim=0, descending=True)seq_tensor = seq_tensor[perm_idx]countries = countries[perm_idx]return create_tensor(seq_tensor), seq_lengths, create_tensor(countries)def trainModel():total_loss = 0for i, (names, countries) in enumerate(trainloader, 1):inputs, seq_lengths, target = make_tensors(names, countries)output = classifier(inputs, seq_lengths)optimizer.zero_grad()loss = criterion(output, target)loss.backward()optimizer.step()total_loss += loss.item()if i % 10 == 0:print(f'[{time_since(start)}] Epoch {epoch}', end='')print(f'[{i * len(inputs)} / {len(trainset)}]', end='')print(f'loss={total_loss / (i * len(inputs))}')return total_lossdef testModel():correct = 0total = len(testset)print("evaluating trained model...")with torch.no_grad():for i, (names, countries) in enumerate(testloader, 1):inputs, seq_lengths, target = make_tensors(names, countries)output = classifier(inputs, seq_lengths)pred = output.max(dim=1, keepdim=True)[1]correct += pred.eq(target.view_as(pred)).sum().item()percent = '%.2f' % (100 * correct / total)print(f'Test set: Accuracy {correct} / {total} {percent}%')return correct / totaltrainset = NameDataset(is_train_set=True)
trainloader = DataLoader(trainset, batch_size=BATCH_SIZE, shuffle=True)
testset = NameDataset(is_train_set=False)
testloader = DataLoader(testset, batch_size=BATCH_SIZE, shuffle=False)N_COUNTRY = trainset.getCountriesNum()if __name__ == '__main__':classifier = RNNClassifier(N_CHARS, HIDDEN_SIZE, N_COUNTRY, N_LAYER)if USE_GPU:device = torch.device("cuda:0")classifier.to(device)criterion = torch.nn.CrossEntropyLoss()optimizer = torch.optim.Adam(classifier.parameters(), lr=0.001)start = time.time()print("Training for %d epochs..." % N_EPOCHS)acc_list = []for epoch in range(1, N_EPOCHS + 1):trainModel()acc = testModel()acc_list.append(acc)# 训练完成后画图epoch = np.arange(1, len(acc_list) + 1, 1)acc_list = np.array(acc_list)plt.figure(figsize=(8,5))plt.plot(epoch, acc_list, marker='o', label='Accuracy')plt.xlabel('Epoch')plt.ylabel('Accuracy')plt.title('RNN Name Classifier Accuracy Curve')plt.grid(True)plt.legend()plt.tight_layout()plt.savefig("accuracy_curve.png")plt.show(block=True)