Symmetric functions and hall polynomials 1.1
本文及后续内容为Symmetric functions and hall polynomials --I. G. MACDONALD 的翻译形式笔记
1. 分拆
本书中我们将考虑的许多对象最终将由分拆参数化。本节的目的是建立一些将在全书使用的符号和术语,并收集一些将在后面使用的关于分拆序的基本结果。
分拆
一个分拆是任何(有限或无限)非负整数的递减序列:
(1.1)λ=(λ1,λ2,…,λr,…)(1.1)\quad\lambda=(\lambda_{1},\lambda_{2},\ldots,\lambda_{r},\ldots)(1.1)λ=(λ1,λ2,…,λr,…)
满足:
λ1⩾λ2⩾…⩾λr⩾…\lambda_{1}\geqslant\lambda_{2}\geqslant\ldots\geqslant\lambda_{r}\geqslant\ldotsλ1⩾λ2⩾…⩾λr⩾…
并且只包含有限多个非零项。我们将发现,不区分那些仅在末尾零串上不同的序列是方便的。因此,例如,我们将(2,1), (2,1,0), (2,1,0,0,…)视为相同的分拆。
(1.1)中的非零λi\lambda_{i}λi称为λ\lambdaλ的部分。部分的数量是λ\lambdaλ的长度,记为l(λ)l(\lambda)l(λ);部分的总和是λ\lambdaλ的权重,记为∣λ∣|\lambda|∣λ∣:
∣λ∣=λ1+λ2+….|\lambda|=\lambda_{1}+\lambda_{2}+\ldots.∣λ∣=λ1+λ2+….
如果∣λ∣=n|\lambda|=n∣λ∣=n,我们说λ\lambdaλ是nnn的一个分拆。nnn的所有分拆的集合记为Pn\mathscr{P}_{n}Pn,所有分拆的集合记为P\mathscr{P}P。特别地,P0\mathscr{P}_{0}P0由唯一一个元素组成,即零的分拆,我们记为000。
有时使用一个表示每个整数作为部分出现次数的符号是方便的:
λ=(1m12m2…rmr…)\lambda=(1^{m_{1}}2^{m_{2}}\ldots r^{m_{r}}\ldots)λ=(1m12m2…rmr…)
意味着恰好有mim_{i}mi个λ\lambdaλ的部分等于iii。这个数
(1.2)mi=mi(λ)=Card{j:λj=i}(1.2)\quad m_{i}=m_{i}(\lambda)=\text{Card}\{j:\lambda_{j}=i\}(1.2)mi=mi(λ)=Card{j:λj=i}
被称为iii在λ\lambdaλ中的重数。
图
一个分拆λ\lambdaλ的图可以形式化地定义为满足1⩽j⩽λi1\leqslant j\leqslant\lambda_{i}1⩽j⩽λi的点集(i,j)∈Z2(i,j)\in Z^{2}(i,j)∈Z2。在绘制此类图形时,我们将采用与矩阵相同的约定:第一坐标iii(行索引)向下递增,第二坐标jjj(列索引)从左向右递增。†^{\dagger}†例如,分拆(5441)的图是

顶行有5个点或节点,第二行有4个,第三行有4个,第四行有1个。更常见的是用方块代替节点,在这种情况下,图是
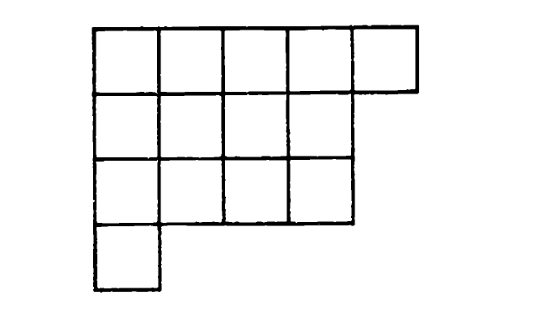
我们通常用相同的符号λ\lambdaλ表示分拆λ\lambdaλ的图。
一个分拆λ\lambdaλ的共轭是分拆λ′\lambda^{\prime}λ′,其图是图λ\lambdaλ的转置,即通过主对角线反射得到的图。因此λi′\lambda^{\prime}_{i}λi′是λ\lambdaλ的第iii列中的节点数,或等价地
(1.3)λi′=Card{j:λj⩾i}.(1.3)\quad\lambda_{i}^{\prime}=\mathrm{Card}\{j:\lambda_{j}\geqslant i\}.(1.3)λi′=Card{j:λj⩾i}.
特别地,λ1′=l(λ)\lambda^{\prime}_{1}=l(\lambda)λ1′=l(λ)且λ1=l(λ′)\lambda_{1}=l(\lambda^{\prime})λ1=l(λ′)。显然λ′′=λ\lambda^{\prime\prime}=\lambdaλ′′=λ。
例如,(5441)的共轭是(43331)。
由(1.2)和(1.3)我们有
(1.4)mi(λ)=λi′−λi+1′.(1.4)\quad m_{i}(\lambda)=\lambda_{i}^{\prime}-\lambda_{i+1}^{\prime}.(1.4)mi(λ)=λi′−λi+1′.
对于每个分拆λ\lambdaλ,我们定义
(1.5)n(λ)=∑i⩾1(i−1)λi,(1.5)\qquad n(\lambda)=\sum_{i\geqslant 1}(i-1)\lambda_{i},(1.5)n(λ)=i⩾1∑(i−1)λi,
因此 n(λ)n(\lambda)n(λ) 是通过将零附加到 λ\lambdaλ 图的顶行中的每个节点,将1附加到第二行中的每个节点,依此类推,所获得的数字之和。将每列中的数字相加,我们看到
(1.6)n(λ)=∑i⩾1(λi′2).(1.6)\quad n(\lambda)=\sum_{i\geqslant 1}\binom{\lambda_{i}^{\prime}}{2}.(1.6)n(λ)=i⩾1∑(2λi′).
分拆的另一个偶尔有用的符号如下,由 Frobenius 提出。假设 λ\lambdaλ 图的主对角线由 rrr 个节点 (i,i)(i,i)(i,i) (1⩽i⩽r)(1\leqslant i\leqslant r)(1⩽i⩽r)组成。令 αi=λi−i\alpha_{i}=\lambda_{i}-iαi=λi−i为λ\lambdaλ的第iii行中(i,i)(i,i)(i,i) 右侧的节点数,对于 1⩽i⩽r1\leqslant i\leqslant r1⩽i⩽r,并令 βi=λi′−i\beta_{i}=\lambda_{i}^{\prime}-iβi=λi′−i为λ\lambdaλ的第iii列中(i,i)(i,i)(i,i)下方的节点数,对于1⩽i⩽r1\leqslant i\leqslant r1⩽i⩽r。我们有 α1>α2>…>αr⩾0\alpha_{1}>\alpha_{2}>\ldots>\alpha_{r}\geqslant 0α1>α2>…>αr⩾0 和 β1>β2>…>βr⩾0\beta_{1}>\beta_{2}>\ldots>\beta_{r}\geqslant 0β1>β2>…>βr⩾0,并且我们将分拆 λ\lambdaλ记为
λ=(α1,…,αr ∣ β1,…,βr)=(α ∣ β).\lambda=(\alpha_{1},\ldots,\alpha_{r}\,|\,\beta_{1},\ldots,\beta_{r})=(\alpha\,|\,\beta).λ=(α1,…,αr∣β1,…,βr)=(α∣β).
显然,(a|β)的共轭是(β|α)。
例如,如果 λ=(5441)\lambda=(5441)λ=(5441),我们有α=(421)\alpha=(421)α=(421)和β=(310)\beta=(310)β=(310)。
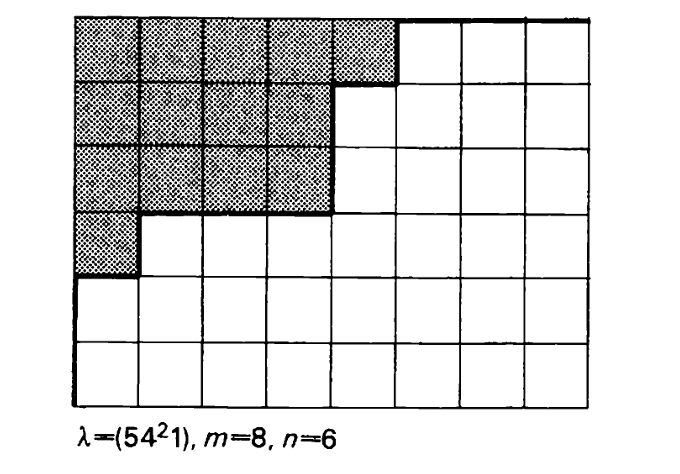
(1.7) 设 λ\lambdaλ是一个分拆,并令m⩾λ1, n⩾λ1′m\geqslant\lambda_{1},\,n\geqslant\lambda_{1}^{\prime}m⩾λ1,n⩾λ1′。那么这m+nm+nm+n个数
λi+n−i(1⩽i⩽n),n−1+j−λj′(1⩽j⩽m)\lambda_{i}+n-i\quad(1\leqslant i\leqslant n),\qquad n-1+j-\lambda_{j}^{\prime}\quad(1\leqslant j\leqslant m)λi+n−i(1⩽i⩽n),n−1+j−λj′(1⩽j⩽m)
是{0,1,2,…,m+n−1}\{0,1,2,\ldots,m+n-1\}{0,1,2,…,m+n−1}的一个排列。
证明。λ\lambdaλ的图包含在(mn)(m^{n})(mn)的图中,这是一个 n x m 矩形。用数字0,1,...,m+n−10,1,...,m+n-10,1,...,m+n−1对λ\lambdaλ与其在(mn)(m^{n})(mn)中的补集之间的边界线(图中粗线标记)的连续段进行编号,从底部开始。附加到垂直线段上的数字是λi+n−i\lambda_{i}+n-iλi+n−i(1⩽i⩽n1 \leqslant i\leqslant n1⩽i⩽n),通过转置,附加到水平线段上的数字是
(m+n−1)−(λj′+m−j)=n−1+j−λj′(1⩽j⩽m).∣(m+n-1)-(\lambda_{j}^{\prime}+m-j)=n-1+j-\lambda_{j}^{\prime}\qquad(1\leqslant j\leqslant m).\quad|\qquad(m+n−1)−(λj′+m−j)=n−1+j−λj′(1⩽j⩽m).∣
令
fλ,n(t)=∑i=1ntλi+n−i.f_{\lambda,n}(t)=\sum_{i=1}^{n}t^{\lambda_{i}+n-i}.fλ,n(t)=i=1∑ntλi+n−i.
那么(1.7)等价于恒等式
(1.7′)fλ,n(t)+tm+n−1fλ′,m(t−1)=(1−tm+n)/(1−t).(1.7^{\prime})\quad f_{\lambda,n}(t)+t^{m+n-1}f_{\lambda^{\prime},m}(t^{-1})=(1-t^{m+n})/(1-t).(1.7′)fλ,n(t)+tm+n−1fλ′,m(t−1)=(1−tm+n)/(1−t).
斜图和表格
如果 λ,μ\lambda,\muλ,μ 是分拆,我们写作 λ⊃μ\lambda\supset\muλ⊃μ 表示 λ\lambdaλ的图包含 μ\muμ 的图,即对所有 i⩾1i\geqslant 1i⩾1有λi⩾μi\lambda_{i}\geqslant\mu_{i}λi⩾μi。集合的差 θ=λ−μ\theta=\lambda-\muθ=λ−μ 称为斜图。例如,如果 λ=(5441)\lambda=(5441)λ=(5441) 且 μ=(432)\mu=(432)μ=(432),则斜图 λ−μ\lambda-\muλ−μ 是下图中阴影区域:
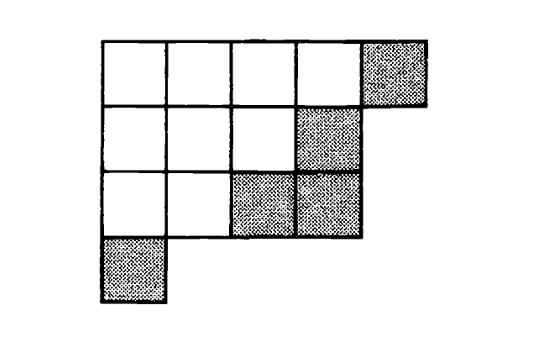
斜图 θ\thetaθ 中的一条路径是θ\thetaθ中方格的一个序列 x0,x1,…,xmx_{0},x_{1},\ldots,x_{m}x0,x1,…,xm,使得 xi−1x_{i-1}xi−1和xix_{i}xi对于 1⩽i⩽m1\leqslant i\leqslant m1⩽i⩽m有一个公共边。 θ\thetaθ的一个子集 φ\varphiφ被称为连通的,如果φ\varphiφ中的任何两个方格可以通过 φ\varphiφ中的一条路径连接。θ\thetaθ的极大连通子集本身是斜图,称为 θ\thetaθ 的连通分支。在上面的例子中,有三个连通分支。
斜图θ=λ−μ\theta=\lambda-\muθ=λ−μ的共轭是 θ′=λ′−μ′\theta^{\prime}=\lambda^{\prime}-\mu^{\prime}θ′=λ′−μ′。令 θi=λi−μi, θi′=λi′−μi′,\theta_{i}= \lambda_{i}-\mu_{i},\,\theta_{i}^{\prime}=\lambda_{i}^{\prime}-\mu_{i}^{\prime},θi=λi−μi,θi′=λi′−μi′, 且
∣θ∣=∑θi=∣λ∣−∣μ∣.|\theta|=\sum\theta_{i}=|\lambda|-|\mu|.∣θ∣=∑θi=∣λ∣−∣μ∣.
一个斜图 θ\thetaθ 是一个水平 m-条带(分别地,垂直 m-条带),如果 ∣θ∣=m|\theta|=m∣θ∣=m 且对每个 i⩾1i\geqslant 1i⩾1 有 θi′⩽1\theta_{i}^{\prime}\leqslant 1θi′⩽1(分别地,θi⩽1\theta_{i}\leqslant 1θi⩽1 )。换句话说,一个水平(分别地,垂直)条带在每列(分别地,行)中至多有一个方格。
如果 θ=λ−μ\theta=\lambda-\muθ=λ−μ ,则 θ\thetaθ 是水平条带的一个充分必要条件是序列λ\lambdaλ和μ\muμ是交错的,即 λ1⩾μ1⩾λ2⩾μ2⩾….\lambda_{1}\geqslant\mu_{1}\geqslant\lambda_{2}\geqslant\mu_{2}\geqslant\ldots.λ1⩾μ1⩾λ2⩾μ2⩾….
一个斜图 θ\thetaθ 是一个边界条带(有些作者也称为斜钩,其他作者称为带),如果 θ\thetaθ 是连通的并且不包含任何 2x2 的方格块,即 θ\thetaθ 的连续行(或列)恰好重叠一个方格。边界条带θ\thetaθ的长度是它包含的方格总数∣θ∣|\theta|∣θ∣,其高度定义为其占据的行数减一。如果我们将边界条带θ\thetaθ视为一组节点而不是方格,那么通过用单位长度的水平或垂直线段连接相邻节点,我们得到一种阶梯,而θ\thetaθ的高度是阶梯中垂直线段或“竖板”的数量。
如果λ=(α1,…,αr ∣ β1,…,βr)\lambda=(\alpha_{1},\ldots,\alpha_{r}\,|\,\beta_{1},\ldots,\beta_{r})λ=(α1,…,αr∣β1,…,βr)且μ=(α2,…,αr ∣ β2,…,βr),\mu=(\alpha_{2},\ldots,\alpha_{r}\,|\,\beta_{2},\ldots,\beta_{r}),μ=(α2,…,αr∣β2,…,βr),那么λ−μ\lambda-\muλ−μ是一个边界条带,称为λ\lambdaλ的边界(或边缘)。
一个 (列严格的)表格 T 是一个分拆序列
μ=λ(0)⊂λ(1)⊂…⊂λ(r)=λ\mu=\lambda^{(0)}\subset\lambda^{(1)}\subset\ldots\subset\lambda^{(r)}=\lambdaμ=λ(0)⊂λ(1)⊂…⊂λ(r)=λ
使得每个斜图 θ(i)=λ(i)−λ(i−1)\theta^{(i)}=\lambda^{(i)}-\lambda^{(i-1)}θ(i)=λ(i)−λ(i−1)( 1⩽i⩽r1\leqslant i\leqslant r1⩽i⩽r ) 是一个水平条带。以图形方式,T 可以通过用数字 iii对斜图θ(i)\theta^{(i)}θ(i)的每个方格编号来描述,对于 1⩽i⩽r1\leqslant i\leqslant r1⩽i⩽r,我们通常将表格视为以这种方式编号的斜图。插入 λ−μ\lambda-\muλ−μ中的数字必须沿着每列严格递增(这解释了形容词“列严格”),并且沿着每行从左到右弱递增。斜图 λ−μ\lambda-\muλ−μ 称为表格 T 的形状,序列 (∣θ(1)∣,...,∣θ(r)∣)(|\theta^{(1)}|,...,|\theta^{(r)}|)(∣θ(1)∣,...,∣θ(r)∣)是 T 的权重。
我们也可以定义行严格表格,要求沿行严格递增且沿列弱递增,但我们不会使用它们;在本书中,表格(不加限定)将指如上定义的列严格表格。
一个标准表格是一个表格 T,它恰好包含数字1,2,...,r1,2,...,r1,2,...,r各一次,因此其权重为(1,1,...,1)(1,1,...,1)(1,1,...,1)。
分拆的加法和乘法
令λ,μ\lambda,\muλ,μ是分拆。我们定义λ+μ\lambda+\muλ+μ为序列λ\lambdaλ与μ\muμ的和:
(λ+μ)i=λi+μi.(\lambda+\mu)_{i}=\lambda_{i}+\mu_{i}.(λ+μ)i=λi+μi.
同时,我们定义λ∪μ\lambda\cup\muλ∪μ为其部分由λ\lambdaλ和μ\muμ的部分按递减顺序排列而成的分拆。例如,若λ=(321)\lambda=(321)λ=(321)且μ=(22)\mu=(22)μ=(22),则λ+μ=(541)\lambda+\mu=(541)λ+μ=(541)且λ∪μ=(32221)\lambda\cup\mu=(32221)λ∪μ=(32221)。
接下来,我们定义λμ\lambda\muλμ为序列λ, μ\lambda,\,\muλ,μ的分量积:
(λμ)i=λiμi.(\lambda\mu)_{i}=\lambda_{i}\mu_{i}.(λμ)i=λiμi.
同时,我们定义λ×μ\lambda\times\muλ×μ为其部分为对所有i⩽l(λ)i\leqslant l(\lambda)i⩽l(λ)和j⩽l(μ)j\leqslant l(\mu)j⩽l(μ)的min(λi,μj)\min(\lambda_{i},\mu_{j})min(λi,μj)按递减顺序排列而成的分拆。
运算+++与∪\cup∪互为对偶,两种乘法运算也是如此:
(λ∪μ)′=λ′+μ′,(\lambda\cup\mu)^{\prime}=\lambda^{\prime}+\mu^{\prime},(λ∪μ)′=λ′+μ′,
(1.8)
(λ×μ)′=λ′μ′.(\lambda\times\mu)^{\prime}=\lambda^{\prime}\mu^{\prime}.(λ×μ)′=λ′μ′.
证明。λ∪μ\lambda\cup\muλ∪μ的图是通过取λ\lambdaλ和μ\muμ的图的各行并按长度递减顺序重新组装而得到的。因此,λ∪μ\lambda\cup\muλ∪μ的第kkk列的长度是λ\lambdaλ和μ\muμ的第kkk列长度之和,即(λ∪μ)k′=λk′+μk′(\lambda\cup\mu)_{k}^{\prime}=\lambda_{k}^{\prime}+\mu_{k}^{\prime}(λ∪μ)k′=λk′+μk′。
其次,λ×μ\lambda\times\muλ×μ的第kkk列的长度等于满足λi⩾k\lambda_{i}\geqslant kλi⩾k且μj⩾k\mu_{j}\geqslant kμj⩾k的序对(i,j)(i,j)(i,j)的数量,因此它等于λk′μk′\lambda_{k}^{\prime}\mu_{k}^{\prime}λk′μk′。从而(λ×μ)k′=λk′μk′(\lambda\times\mu)_{k}^{\prime}=\lambda_{k}^{\prime}\mu_{k}^{\prime}(λ×μ)k′=λk′μk′。
序关系
令LnL_{n}Ln表示集合Pn\mathscr{P}_{n}Pn(n 的分拆的集合)上的逆字典序:即,LnL_{n}Ln是Pn×Pn\mathscr{P}_{n}\times\mathscr{P}_{n}Pn×Pn的子集,由所有(λ,μ)(\lambda,\mu)(λ,μ)组成,使得要么λ=μ\lambda=\muλ=μ,要么第一个非零差值λi−μi\lambda_{i}-\mu_{i}λi−μi是正的。LnL_{n}Ln是一个全序。例如,当n=5n=5n=5时,L5L_{5}L5将P5\mathscr{P}_{5}P5排列为序列
(5),(41),(32),(312),(221),(213),(15).(5),(41),(32),(31^{2}),(2^{2}1),(2^{1}3),(1^{5}).(5),(41),(32),(312),(221),(213),(15).
Pn\mathscr{P}_{n}Pn上的另一个全序是Ln′L^{\prime}_{n}Ln′,即所有(λ,μ)(\lambda,\mu)(λ,μ)的集合,使得要么λ=μ\lambda=\muλ=μ,要么第一个非零差值λi∗−μi∗\lambda_{i}^{*}-\mu_{i}^{*}λi∗−μi∗是负的,其中λi∗=λn+1−i\lambda_{i}^{*}=\lambda_{n+1-i}λi∗=λn+1−i。一旦n⩾6n\geqslant 6n⩾6,序关系Ln,Ln′L_{n},L_{n}^{\prime}Ln,Ln′就是不同的。例如,如果λ=(313)\lambda=(31^{3})λ=(313)和μ=(23)\mu=(2^{3})μ=(23),我们有(λ,μ)∈L6(\lambda,\mu)\in L_{6}(λ,μ)∈L6且(μ,λ)∈L6′(\mu,\lambda)\in L^{\prime}_{6}(μ,λ)∈L6′。
(1.9) 设λ,μ∈Pn.\lambda,\mu\in\mathscr{P}_{n}.λ,μ∈Pn.那么
(λ,μ)∈Ln′⇔(μ′,λ′)∈Ln.(\lambda,\mu)\in L_{n}^{\prime}\Leftrightarrow(\mu^{\prime},\lambda^{\prime})\in L_{n}.(λ,μ)∈Ln′⇔(μ′,λ′)∈Ln.
证明。假设(λ,μ)∈Ln′(\lambda,\mu)\in L^{\prime}_{n}(λ,μ)∈Ln′且λ≠μ.\lambda\neq\mu.λ=μ.那么对于某个整数i⩾1i\geqslant 1i⩾1,我们有λi<μi\lambda_{i}<\mu_{i}λi<μi,且对于j>ij>ij>i有λj=μj.\lambda_{j}=\mu_{j}.λj=μj.如果我们令k=λik=\lambda_{i}k=λi并考虑λ\lambdaλ和μ\muμ的图,我们立即看到对于1⩽j⩽k1\leqslant j\leqslant k1⩽j⩽k有λj′=μj′\lambda^{\prime}_{j}=\mu^{\prime}_{j}λj′=μj′,并且λk+1′<μk+1′\lambda^{\prime}_{k+1}<\mu^{\prime}_{k+1}λk+1′<μk+1′,因此(μ′,λ′)∈Ln(\mu^{\prime},\lambda^{\prime})\in L_{n}(μ′,λ′)∈Ln。反之类似可证。
比LnL_{n}Ln或Ln′L^{\prime}_{n}Ln′都更重要的一个序是Pn\mathscr{P}_{n}Pn上的自然(偏)序NnN_{n}Nn(有些作者也称为优势偏序),其定义如下:
(λ,μ)∈Nn⇔λ1+…+λi⩾μ1+…+μi对所有i⩾1.(\lambda,\mu)\in N_{n}\Leftrightarrow\lambda_{1}+\ldots+\lambda_{i}\geqslant\mu_{1}+\ldots+\mu_{i}\quad\text{对所有}i\geqslant 1.(λ,μ)∈Nn⇔λ1+…+λi⩾μ1+…+μi对所有i⩾1.
一旦 n≥6, NnN_{n}Nn 就不是一个全序。例如,分拆(313)和(23)关于 N6N_{6}N6 是不可比的。
我们将用λ⩾μ\lambda\geqslant\muλ⩾μ代替(λ,μ)∈Nn.(\lambda,\mu)\in N_{n}.(λ,μ)∈Nn.
(1.10) 设λ,μ∈Pn.\lambda,\mu\in\mathscr{P}_{n}.λ,μ∈Pn.那么
λ⩾μ⇒(λ,μ)∈Ln∩Ln′.\lambda\geqslant\mu\Rightarrow(\lambda,\mu)\in L_{n}\cap L_{n}^{\prime}.λ⩾μ⇒(λ,μ)∈Ln∩Ln′.
证明。假设λ⩾μ.\lambda\geqslant\mu.λ⩾μ.那么要么λ1>μ1,\lambda_{1}>\mu_{1},λ1>μ1,此时(λ,μ)∈Ln,(\lambda,\mu)\in L_{n},(λ,μ)∈Ln,要么λ1=μ1.\lambda_{1}=\mu_{1}.λ1=μ1.在那种情况下,要么λ2>μ2,\lambda_{2}>\mu_{2},λ2>μ2,此时再次(λ,μ)∈Ln,(\lambda,\mu)\in L_{n},(λ,μ)∈Ln,要么λ2=μ2.\lambda_{2}=\mu_{2}.λ2=μ2.以此方式继续,我们看到(λ,μ)∈Ln.(\lambda,\mu)\in L_{n}.(λ,μ)∈Ln.
此外,对于每个i⩾1i\geqslant 1i⩾1,我们有
λi+1+λi+2+…=n−(λ1+…+λi)⩽n−(μ1+…+μi)=μi+1+μi+2+…\begin{align*}\lambda_{i+1}+\lambda_{i+2}+\ldots&=n-(\lambda_1+\ldots+\lambda_i)\\ &\leqslant n-(\mu_1+\ldots+\mu_i)\\ &=\mu_{i+1}+\mu_{i+2}+\ldots\end{align*}λi+1+λi+2+…=n−(λ1+…+λi)⩽n−(μ1+…+μi)=μi+1+μi+2+…
因此,与之前相同的推理表明(λ,μ)∈Ln′.(\lambda,\mu)\in L^{\prime}_{n}.(λ,μ)∈Ln′.
注意: 通常 Nn=Ln∩Ln′N_{n} = L_{n}\cap L^{\prime}_{n}Nn=Ln∩Ln′不成立。例如,当n=12n=12n=12且λ=(632), μ=(5212)\lambda=(63^{2}),\,\mu=(5^{2}1^{2})λ=(632),μ=(5212)时,我们有(λ,μ)∈L12∩L12′(\lambda,\mu)\in L_{12}\cap L^{\prime}_{12}(λ,μ)∈L12∩L12′,但(λ,μ)∉N12.(\lambda,\mu)\notin N_{12}.(λ,μ)∈/N12.
(1.11) 设λ,μ∈Pn.\lambda,\mu\in\mathscr{P}_{n}.λ,μ∈Pn.那么
λ⩾μ⇔μ′⩾λ′.\lambda\geqslant\mu\Leftrightarrow\mu^{\prime}\geqslant\lambda^{\prime}.λ⩾μ⇔μ′⩾λ′.
证明。显然只需证明一个蕴含关系。那么假设μ′⩾̸λ′.\mu^{\prime}\not\geqslant\lambda^{\prime}.μ′⩾λ′.那么对于某个i⩾1i\geqslant 1i⩾1,我们有
λ1′+…+λj′⩽μ1′+…+μj′(1⩽j⩽i−1)\lambda_{1}^{\prime}+\ldots+\lambda_{j}^{\prime}\leqslant\mu_{1}^{\prime}+\ldots+\mu_{j}^{\prime}\qquad(1\leqslant j\leqslant i-1)λ1′+…+λj′⩽μ1′+…+μj′(1⩽j⩽i−1)
且
(1)λ1′+…+λi′>μ1′+…+μi′(1)\qquad\lambda_{1}^{\prime}+\ldots+\lambda_{i}^{\prime}>\mu_{1}^{\prime}+\ldots+\mu_{i}^{\prime}(1)λ1′+…+λi′>μ1′+…+μi′
由此得出λi′>μi′\lambda_{i}^{\prime}>\mu_{i}^{\prime}λi′>μi′。
令l=λi′, m=μi′.l=\lambda^{\prime}_{i},\,m=\mu^{\prime}_{i}.l=λi′,m=μi′.由(1)得出
(2)λi+1′+λi+2′+…<μi+1′+μi+2′+…(2)\qquad\lambda_{i+1}^{\prime}+\lambda_{i+2}^{\prime}+\ldots<\mu_{i+1}^{\prime}+\mu_{i+2}^{\prime}+\ldots(2)λi+1′+λi+2′+…<μi+1′+μi+2′+…
现在λi+1′+λi+2′+…\lambda^{\prime}_{i+1}+\lambda^{\prime}_{i+2}+\ldotsλi+1′+λi+2′+…等于位于λ\lambdaλ图第iii列右侧的节点数,因此
λi+1′+λi+2′+…=∑j=1l(λj−i).\lambda_{i+1}^{\prime}+\lambda_{i+2}^{\prime}+\ldots=\sum_{j=1}^{l}(\lambda_{j}-i).λi+1′+λi+2′+…=j=1∑l(λj−i).
同样地
μi+1′+μi+2′+…=∑j=1m(μj−i).\mu_{i+1}^{\prime}+\mu_{i+2}^{\prime}+\ldots=\sum_{j=1}^{m}(\mu_{j}-i).μi+1′+μi+2′+…=j=1∑m(μj−i).
因此由(2)我们有
(3)∑j=1m(μj−i)>∑j=1l(λj−i)⩾∑j=1m(λj−i)(3)\quad\sum_{j=1}^{m}(\mu_{j}-i)>\sum_{j=1}^{l}(\lambda_{j}-i)\geqslant\sum_{j=1}^{m}(\lambda_{j}-i)(3)j=1∑m(μj−i)>j=1∑l(λj−i)⩾j=1∑m(λj−i)
其中右边的不等式成立是因为 l>ml>ml>m 且对于1⩽j⩽l1\leqslant j\leqslant l1⩽j⩽l有λj⩾i\lambda_{j}\geqslant iλj⩾i。由(3)我们有
μ1+…+μm>λ1+…+λm\mu_{1}+\ldots+\mu_{m}>\lambda_{1}+\ldots+\lambda_{m}μ1+…+μm>λ1+…+λm
因此λ≠μ.\lambda\neq\mu.λ=μ.
