机器学习基础入门（第四篇）：无监督学习与聚类方法

目录

一、前言

二、无监督学习的基本概念

1. 定义

2. 特点

3. 常见任务

三、聚类（Clustering）的核心思想

1. 定义

2. 应用场景

四、常见聚类方法

1. K-Means 聚类

原理

优缺点

Python 实现

2. 层次聚类（Hierarchical Clustering）

原理

Python 实现

3. DBSCAN（基于密度的聚类）

原理

Python 实现

4. 高斯混合模型（GMM）

原理

Python 实现

五、聚类效果评估

六、无监督学习的挑战与趋势

1. 挑战

2. 发展趋势

七、总结

---

一、前言

在前几篇文章中，我们学习了机器学习的基础知识、分类体系以及监督学习的原理与经典算法。监督学习在实际中非常常见，但它有一个关键前提：需要大量带标签的数据。

然而在现实中，标注往往昂贵甚至不可行：

电商平台积累了大量用户行为数据，却没有人逐一标注“用户群体”；

医学影像数据庞大，但人工标注需要专家参与，耗费极高；

工业传感器产生连续监测数据，但只有少量“故障”样本。

在这些场景中，无监督学习（Unsupervised Learning） 就显得尤为重要。它不依赖标签，而是通过分析数据特征和分布，自动发现潜在规律。本文将重点介绍无监督学习的代表方法——聚类（Clustering）。

---

二、无监督学习的基本概念

1. 定义

无监督学习是指：在数据没有标签的情况下，算法通过分析样本特征，发现数据内部结构和模式。

如果说监督学习是“老师给出题目和答案，学生学会解题”，那么无监督学习就是“学生自己在题目中寻找规律”。

2. 特点

• 不需要标签，适合数据预处理阶段；

• 结果带有探索性和启发性；

• 常用于数据挖掘、模式发现和特征学习。

3. 常见任务

• 聚类（Clustering）

• 降维（Dimensionality Reduction）

• 异常检测（Anomaly Detection）

• 关联规则学习（Association Rule Learning）

---

三、聚类（Clustering）的核心思想

1. 定义

聚类是无监督学习最典型的任务，目标是：

将数据划分成若干组（簇），使同一簇的样本尽可能相似，不同簇的样本尽可能不同。

2. 应用场景

• 电商：客户群体划分，支持精准营销；

• 金融：异常交易检测；

• 医学：基因表达数据分组，探索疾病亚型；

• 图像处理：图像分割、压缩；

• NLP：新闻自动分组、搜索结果聚类。

---

四、常见聚类方法

1. K-Means 聚类

原理

K-Means 通过迭代优化，将样本分配到最近的簇中心：

1. 随机选择 K 个初始中心；

2. 将每个样本分配到最近的中心；

3. 更新每个簇的中心（均值）；

4. 重复 2-3 直到收敛。

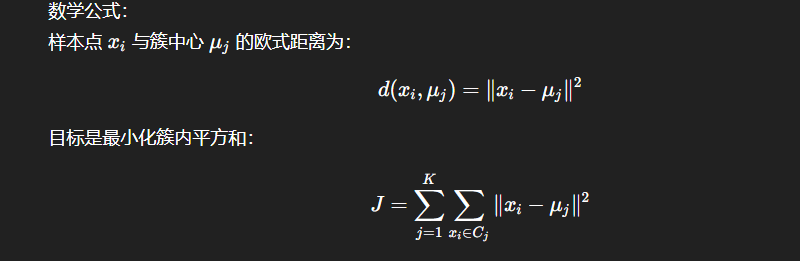
优缺点

• 优点：简单高效，适合大规模数据；

• 缺点：需要指定 K，对初始中心敏感，只能发现球形簇。

Python 实现

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans# 生成模拟数据
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=42)# 训练 K-Means
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)# 可视化
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=30, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, marker='x')
plt.title("K-Means Clustering")
plt.show()

运行结果：可以看到数据点被分为 4 个簇，每个簇中心用红色 “X” 标记。

---

2. 层次聚类（Hierarchical Clustering）

原理

层次聚类通过不断合并或拆分簇，形成树状的层级结构：

• 自底向上（凝聚型）：每个样本独立为簇，逐步合并；

• 自顶向下（分裂型）：所有样本为一类，逐步拆分。

Python 实现

import scipy.cluster.hierarchy as sch
from sklearn.cluster import AgglomerativeClustering# 层次聚类
hc = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
y_hc = hc.fit_predict(X)# 树状图
dendrogram = sch.dendrogram(sch.linkage(X, method='ward'))
plt.title("Hierarchical Clustering Dendrogram")
plt.show()

树状图可以帮助选择合适的簇数。

---

3. DBSCAN（基于密度的聚类）

原理

DBSCAN 根据样本密度定义簇：

• 核心点：邻域内点数 ≥ MinPts；

• 密度可达：可以从核心点到达的点；

• 噪声点：无法归类到任何簇的点。

Python 实现

from sklearn.cluster import DBSCANdbscan = DBSCAN(eps=0.5, min_samples=5)
y_db = dbscan.fit_predict(X)plt.scatter(X[:, 0], X[:, 1], c=y_db, cmap='plasma', s=30)
plt.title("DBSCAN Clustering")
plt.show()

特点：不需要指定簇数，可识别任意形状的簇，但对参数 eps、MinPts 敏感。

---

4. 高斯混合模型（GMM）

原理

GMM 假设数据由多个高斯分布混合而成，通过 EM 算法估计参数，输出每个点属于簇的概率（软聚类）。

Python 实现

from sklearn.mixture import GaussianMixturegmm = GaussianMixture(n_components=4, covariance_type='full')
y_gmm = gmm.fit_predict(X)plt.scatter(X[:, 0], X[:, 1], c=y_gmm, cmap='coolwarm', s=30)
plt.title("Gaussian Mixture Model Clustering")
plt.show()

特点：比 K-Means 更灵活，能发现椭圆簇。

---

五、聚类效果评估

无监督学习没有“标准答案”，评估聚类效果比较困难。常见方法：

1. 内部指标（基于样本间距离）：

   • 轮廓系数（Silhouette Coefficient）：取值 [-1,1]，越大越好。

   • Davies-Bouldin 指数。

2. 外部指标（有少量标签时可用）：

   • 调整兰德指数（ARI）。

   • 互信息（Mutual Information）。

3. 可视化评估：用 PCA、t-SNE 降维后直观查看。

from sklearn.metrics import silhouette_scorescore = silhouette_score(X, y_kmeans)
print("K-Means 轮廓系数:", score)

---

六、无监督学习的挑战与趋势

1. 挑战

• 簇数选择困难；

• 高维空间中“距离度量失效”；

• 聚类结果可解释性弱。

2. 发展趋势

• 深度聚类：结合神经网络和聚类方法（如 DEC）。

• 自监督学习：通过伪标签提升无监督能力（如 SimCLR, BYOL）。

• 可解释聚类：让聚类结果更直观、可用于决策。

---

七、总结

无监督学习是机器学习的重要分支，在缺乏标注数据的情况下尤其有价值。其中，聚类是最典型的任务，主要方法包括：

K-Means：高效、简单；

层次聚类：能揭示层次关系；

DBSCAN：发现任意形状簇；

GMM：基于概率的软聚类。

借助 Python 的 scikit-learn，我们能快速实现这些算法并进行可视化。聚类不仅帮助我们更好地理解数据，还能为后续建模和应用奠定基础。