深度学习基础：从原理到实践——第一章感知机（中）

1.3感知机的数学模型

1.3.1感知机的数学定义

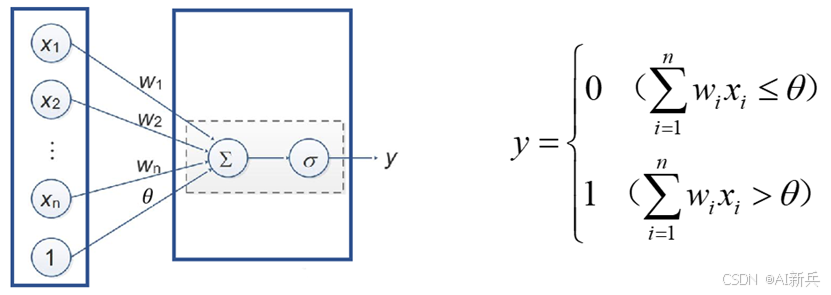
图4感知机模型

感知机的数学模型可以形式化地定义为：给定输入空间（特征空间）X ⊆ Rⁿ，输出空间 Y = {0, 1}。感知机是定义在特征空间上的如下函数：

f(x) = sign(w·x + b)

其中，w ∈ Rⁿ是权重向量，b ∈ R 是偏置，w・x 表示向量 w 和 x 的点积运算，sign (・) 是符号函数，定义为：

sign(z) = { 1, z ≥ 0; 0, z < 0 }

权重向量 w 和偏置 b 统称为感知机的模型参数。权重向量 w 决定了输入特征的重要性，偏置 b 则控制了分类边界的位置。从几何意义上看，w・x + b = 0 定义了特征空间中的一个超平面，称为分离超平面。

1.3.2权重和偏置的几何意义

在感知机模型中，权重向量 w 和偏置 b 具有明确的几何意义。权重向量 w 是分类超平面的法向量，它决定了超平面的方向。偏置 b 则决定了超平面距离原点的远近。

具体来说，对于超平面 w・x + b = 0，任意一点 x 到超平面的距离可以用公式表示为：

d = |w·x + b| / ||w||

其中 ||w|| 表示权重向量 w 的 L2 范数。这个距离公式揭示了感知机的分类机制：样本点到超平面的距离决定了分类的置信度。距离越大，分类的确定性越高；距离越小，分类的不确定性越大。

权重向量 w 的方向还决定了特征空间中不同方向上的重要性。权重的绝对值越大，对应的特征对分类结果的影响就越大。例如，如果 w₁的绝对值远大于其他权重分量，说明第一个特征在分类中起着主导作用。偏置 b 的作用类似于截距，它调整了超平面在特征空间中的位置，使得分类边界可以在空间中自由移动，而不改变其方向。

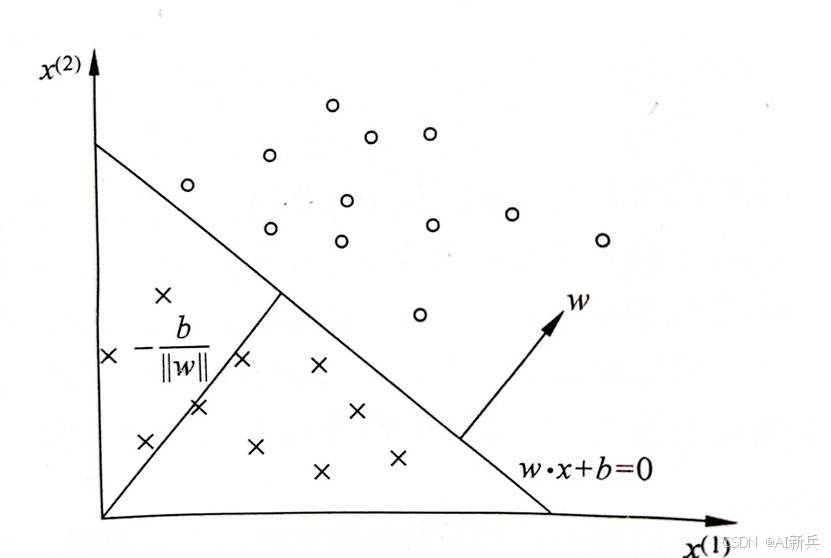
图 5感知机是一个线性分类器

1.3.3激活函数的选择与作用

感知机使用符号函数 sign (・) 作为激活函数，这是一个阶跃函数，在零点处不连续。激活函数的作用是将线性组合的结果转换为离散的分类标签。除了符号函数，感知机也可以使用其他激活函数，如 sigmoid 函数、tanh 函数等，但这些激活函数主要用于多层感知机中。

常用激活函数如下：

1）阶跃函数

激活函数以阈值为界，一旦输入超过阈值，就切换输出。这样的函数称为“阶跃函数”。

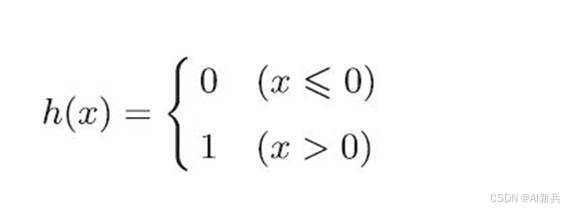
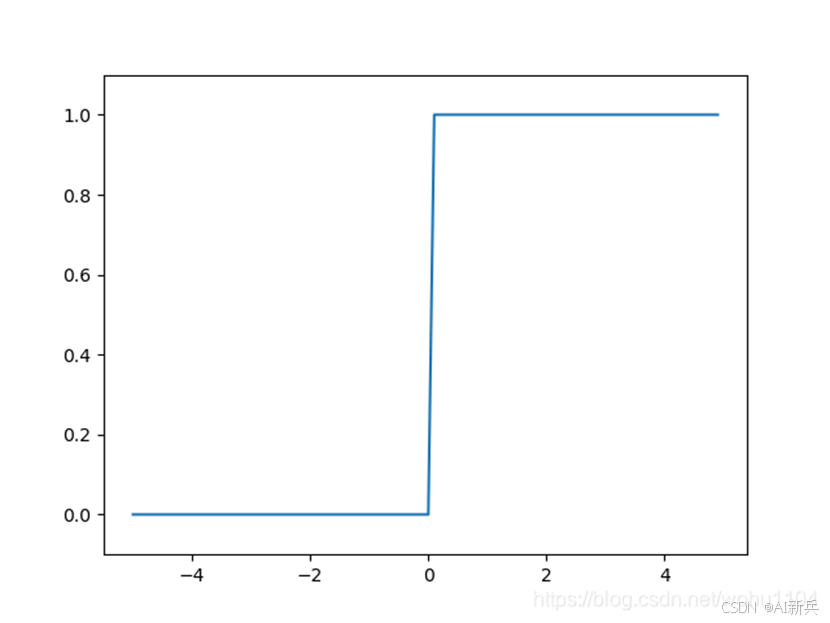
图 6阶跃函数公式及图形

2）sigmoid 函数

神经网络中经常使用的一个激活函数是sigmoid 函数：

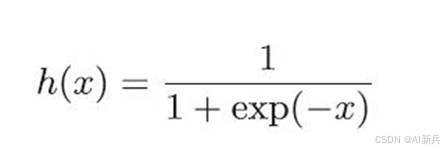
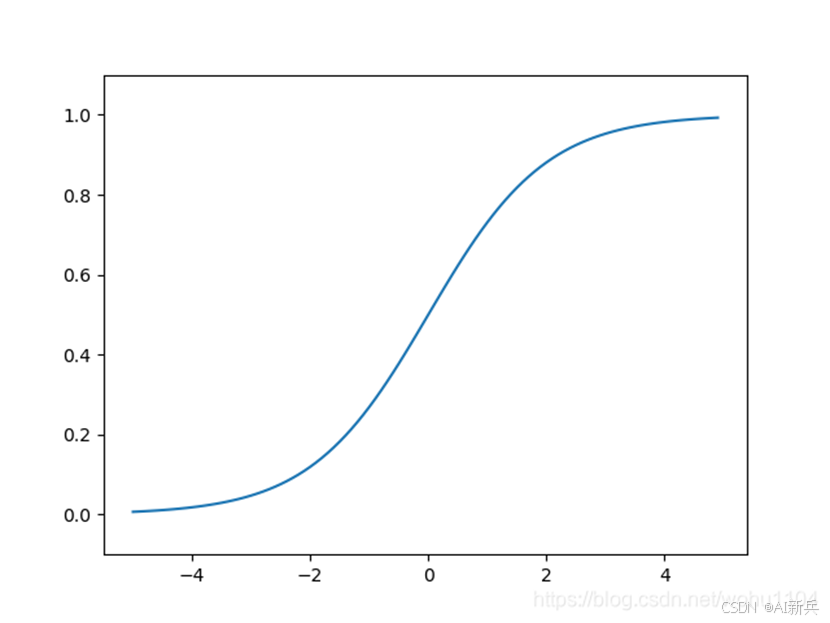
图 7 sigmoid 函数公式及图形

3）ReLU 函数

在神经网络发展的历史上， sigmoid 函数很早就开始被使用了，而最近则主要使用 ReLU 线性整流函数 ( Rectified Linear Unit )函数。

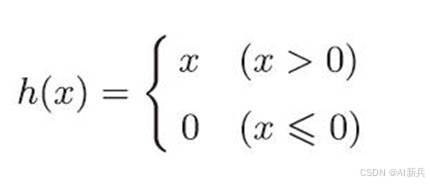
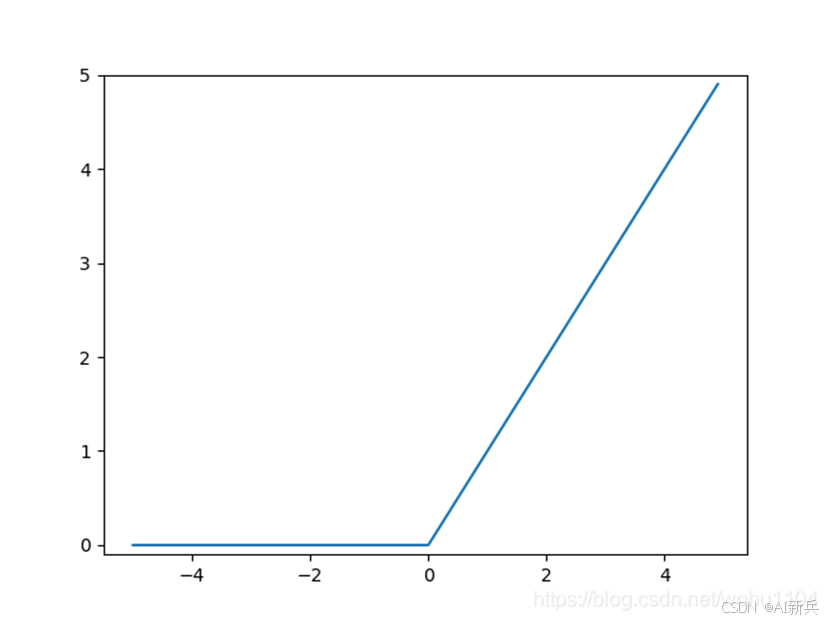
图 8 ReLU 函数公式及图形

4）tanh 函数

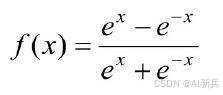
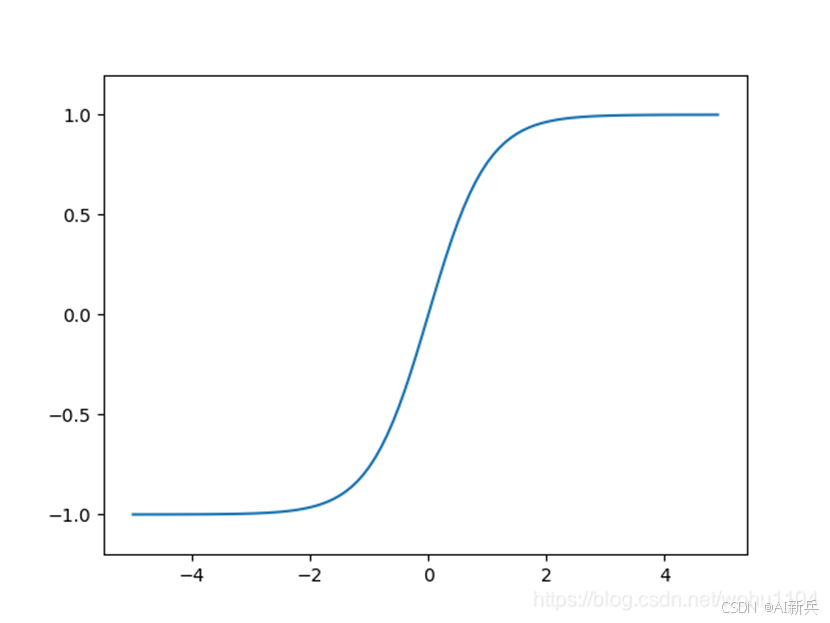
图 9 tanh 函数公式及图形

激活函数的选择对感知机的性能有重要影响。符号函数的优点是计算简单，输出明确，但它的不连续性导致无法使用梯度下降等基于导数的优化算法。这也是为什么感知机需要使用专门的学习算法，而不能直接应用通用的梯度下降方法。

在实际应用中，有时会使用平滑的激活函数来近似符号函数，如使用 sigmoid 函数的阈值输出。但这种做法改变了感知机的本质特性，使其不再是严格意义上的线性分类器。因此，在单层感知机中，符号函数仍然是最标准的选择。