PID--积分项I
含有比例项和积分项的PID输出值：
积分项的输出值取决于0~t所有时刻误差的积分，与历史时刻有关。积分项将历史所有时刻的误差累积，乘上积分项系数
后作为积分项输出值, 积分项用于弥补纯比例项产生的稳态误差，若系统持续产生误差，则积分项会不断累积误差，直到控制器产生动作，让稳态误差消失.
越大，积分项权重越大，稳态误差消失越快，但系统滞后性也会随之增加
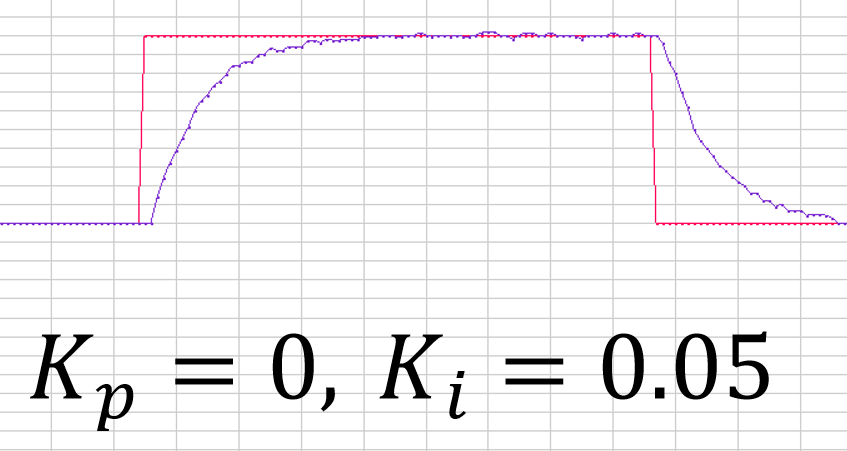
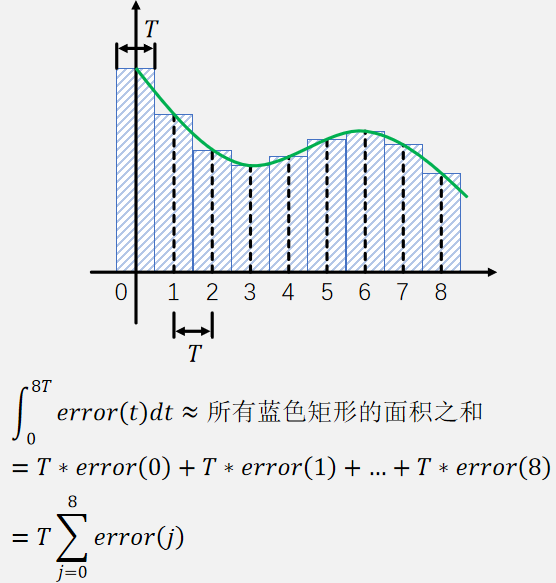我们的软件层不能一直只监控误差的积分，即使是加了FreeRTOS等实时操作系统也做不到硬件那种连续性，所有我们的积分是离散化的，每个周期T采样一次进行积分。如果我们抛出比例项，只保留积分项，那从零时刻起，Out会逐渐逼近Target，而且在这个过程中，Error是不断减少的，所以越靠近Target增长越慢，这就是滞后性，积分项能确保Actual达到Target（前提是Target值合理，Out取最大值前Actual能达到Target），积分项存在，则只要存在误差，Out就会不断改变，无论初态是高是低，经积分项作用最终都会达到Target
消除稳态误差：
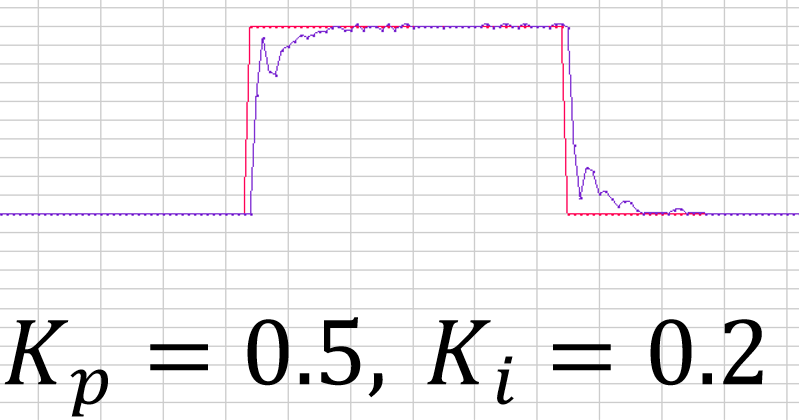
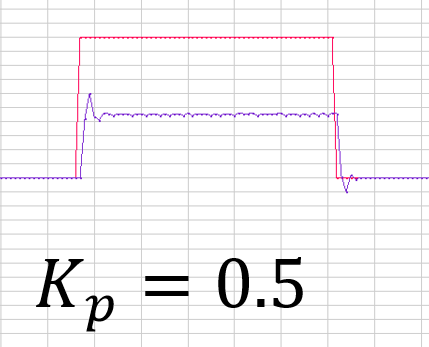
通过积分项的作用，稳态误差被消除，但是也埋下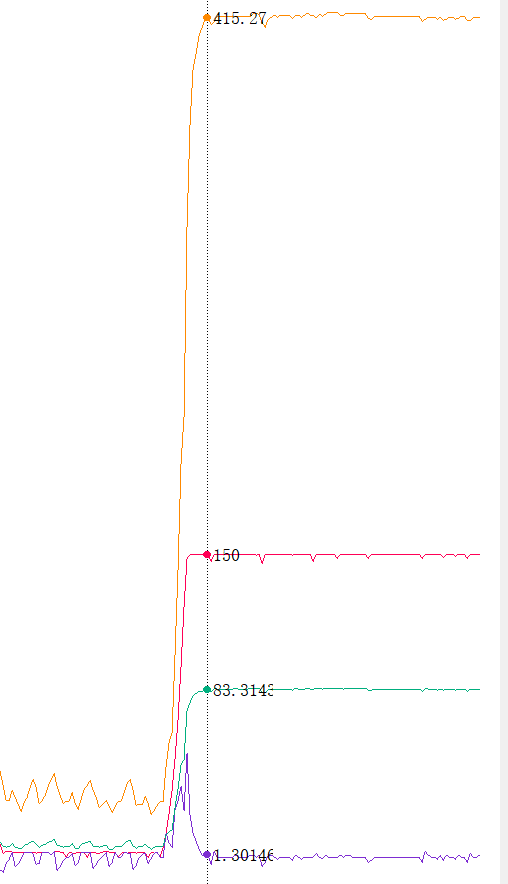
了一个问题，即Out值与历史有关了，积分值是一个较大的值，对于电机驱动来说如果Target设置为150，紫色是误差值 ，橙色是积分值，红色目标值Target，绿色是Out值。 此时的K_P = K_I = 0.2 积分项的积分值在很短的时间内就积累起来了，而比例项的误差值涨幅不高并且之后降为了0，所以PI控制的情况下最终实际上Out只取决于积分项I了。 我们设置的K_I在这种电机控制下占比还是比较的大，没有太高普遍参考意义 如果这里K_I是0.05或更小值是，积分值会非常高，这会降低响应速度，增大之后性（这里的响应不同于比例项P的响应，比例项到达稳态误差后，积分项还没从之前的历史影响走出来，作用的较慢）
积分限幅
要解决的问题：如果执行器因为卡住、断电、损坏等原因不能消除误差，则误差积分会无限制加大，进而达到深度饱和状态，此时PID控制器会持续输出最大的调控力，即使后续执行器恢复正常，PID控制器在短时间内也会维持最大的调控力，直到误差积分从深度饱和状态退出 积分限幅
实现思路：对误差积分或积分项输出进行判断，如果幅值超过指定阈值，则进行限制
ErrorInt += Error0;
if(ErrorInt > Limit){ErrorInt = Limit;}
else if(ErrorInt < -Limit){ErrorInt = -Limit;}
Out = K_P * Error0 + K_I * ErrorInt;
Int是积分integral的缩写
Limit一般设置为Out的最大值，令Limit = K_I * ErrorInt。
也可以直接对积分项I进行限幅
I += K_I * Error0;
if(I > Limit){I = Limit;}
else if(I < -Limit){I = -Limit;}
Out = K_P * Error0 + I + K_D * (Error0 - Error1);
积分分离
对于一些精准调控，如转盘位置，积分项导致的滞后性会导致当Actual达到Target时Out不能及时的归零，需要积分抵消才能停止。
要解决的问题：积分项作用一般位于调控后期，用来消除持续的误差，调控前期一般误差较大且不需要积分项作用，如果此时仍然进行积分，则调控进行到后期时，积分项可能已经累积了过大的调控力，这会导致超调
积分分离实现思路：对误差大小进行判断，如果误差绝对值小于指定阈值，则加入积分项作用，反之，则直接将误差积分清零或不加入积分项作用
//求绝对值
if(Error0 < 0){ErrorValve = -Error0;}
else{ErrorValve = Error0;}
//阈值比较
if(K_I != 0 && ErrorValve <= Value){ErrorInt += Error0;}
else{ErrorInt = 0;}Out = K_P * Error0 + K_I * ErrorInt;阈值Value根据稳态误差确定，使K_I = 0，观察稳态误差，并且以此为基础适当扩大阈值，给积分项一定预热时间。
积分激活法：
ErrorInt += Error0;
uint8_t i = 0;if(Error0 < 0){ErrorValve = -Error0;}
else{ErrorValve = Error0;}
if(K_I != 0 && ErrorValve <= Value){i = 1;}
else{i = 0;}Out = K_P * Error0 + i * K_I * ErrorInt;变速积分
要解决的问题：积分项作用一般位于调控后期，用来消除持续的误差，调控前期一般误差较大且不需要积分项作用，如果此时仍然进行积分，则调控进行到后期时，积分项可能已经累积了过大的调控力，这会导致超调。
变速积分一般是对积分分离的优化。
积分分离实现思路：对误差大小进行判断，如果误差绝对值小于指定阈值，则加入积分项作用，反之，则直接将误差积分清零或不加入积分项作用
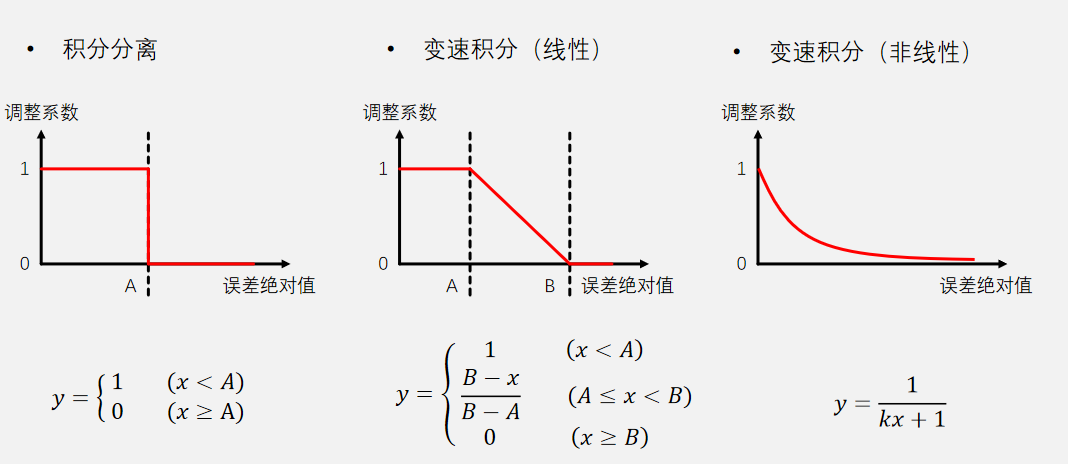
if(Error0 < 0){ErrorValve = -Error0;}
else{ErrorValve = Error0;}
if(K_I != 0 && ErrorValve <= Value){i = 1 /(k * ErrorValve + 1);}
else{i = 0;}
ErrorInt += i * Error0;
Out = K_P * Error0 + i * K_I * ErrorInt + K_D * (Error0 - Error1);积分项在弥补比例项不足的同时也产生了新的问题，根据实际情况合理调参，进行优化，才能使算法达到一个比较理想的状态。