吃透大数据算法-霍夫曼编码(Huffman Coding)
一、趣味故事场景:智慧信使的“摩斯密码”
想象一下,在没有电话和互联网的古代,一个王国需要频繁地传递军情。信使是唯一的希望,但他们长途跋涉,体力有限。国王发现,军情信件里,“进攻”、“撤退”、“粮草”这几个词出现得特别多,而像“跳舞”、“唱歌”这类词几乎从不出现。
聪明的信使队长霍夫曼想出了一个绝妙的主意:我们别用一样长的信号来表示所有词了!
他规定:
- 常用词(如“进攻敌人的中军”)用非常短的信号,比如一声鼓响“咚-!”。
- 不常用词(如“粮草向后撤退”)用稍长的信号,比如“咚-咚!”。
- 罕见词(如“跳舞迷惑敌人”)就用很长的信号,比如“咚-咚-咚!”。
这样一来,大部分信件都变得非常简短,信使们省了不少力气,传递效率大大提高。霍夫曼队长这套“为常客铺捷径,为稀客绕远路”的信号系统,就是霍夫曼编码的核心思想。
为常客铺捷径,为稀客绕远路,即高频元素用短码,低频元素用长码,实现数据总长度的最短化。
二、霍夫曼树构建过程
将军需要用 “鼓响” 传递 3 个指令,根据指令使用频率设计不同长度的鼓响 —— 先给每个指令分配出现频率(基于军营日常传令次数统计),再一步步构建霍夫曼树,最终确定鼓响信号。
前提:确定指令与频率
首先明确 3 个传令指令及其 “月度使用频率”(频率越高,需要越短的鼓响):
| 传令指令 | 月度使用频率 | 需求(鼓响长度) |
|---|---|---|
| 进攻敌人的中军 | 10 次 | 最短(少鼓响) |
| 粮草向后撤退 | 5 次 | 中等(中鼓响) |
| 跳舞迷惑敌人 | 3 次 | 最长(多鼓响) |
霍夫曼树构建:3 步定鼓响
霍夫曼树的核心规则:每次选频率最小的两个节点合并,新节点频率 = 两节点频率之和,重复直到只剩 1 个根节点。
步骤 1:初始化 —— 所有指令作为 “初始节点”
先将 3 个指令按 “频率升序” 排列,每个指令都是独立的叶子节点(还没有父节点):
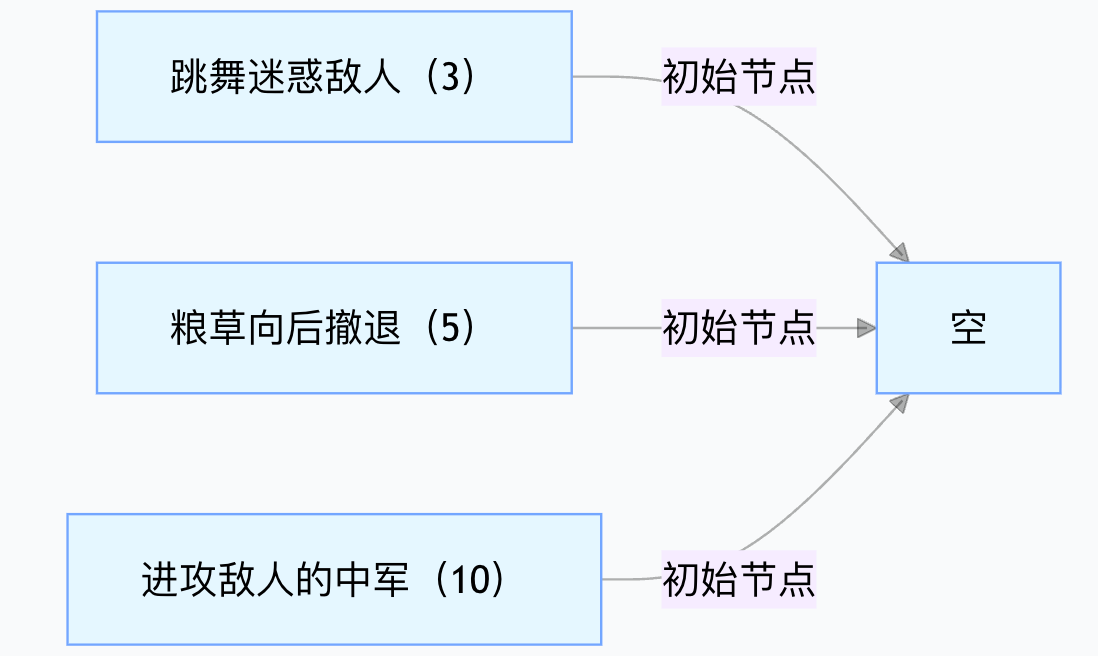
此时 3 个节点都是 “待合并状态”,频率从小到大:3 < 5 < 10
步骤 2:第一次合并 —— 选频率最小的两个节点,从低频开始合并:天然让高频 “站上层”
取频率最小的两个节点(3 和 5),合并成一个 “新父节点”,新节点频率 = 3+5=8: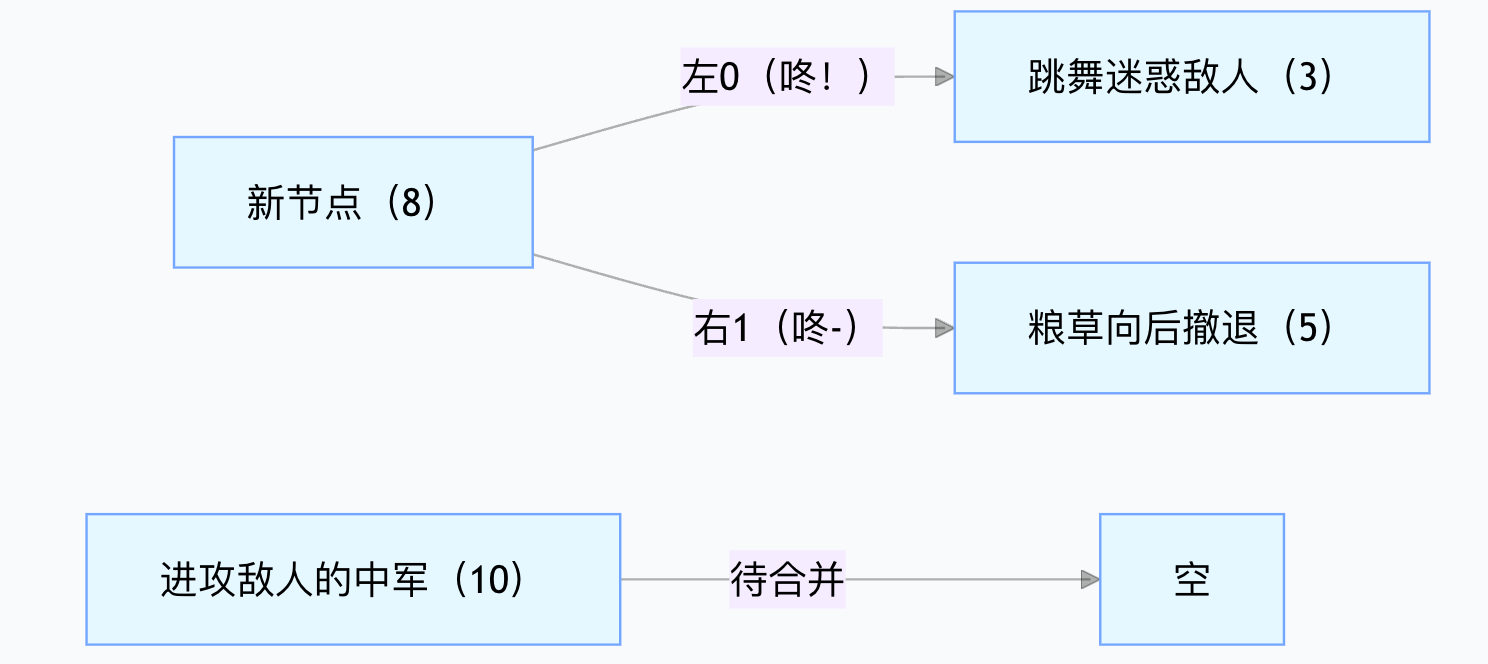
现在待合并节点变为:新节点(8)、进攻敌人的中军(10),按频率升序:8 < 10
步骤 3:第二次合并 —— 合并剩余两个节点
取剩余两个节点(8 和 10),合并成 “根节点”,根节点频率 = 8+10=18:
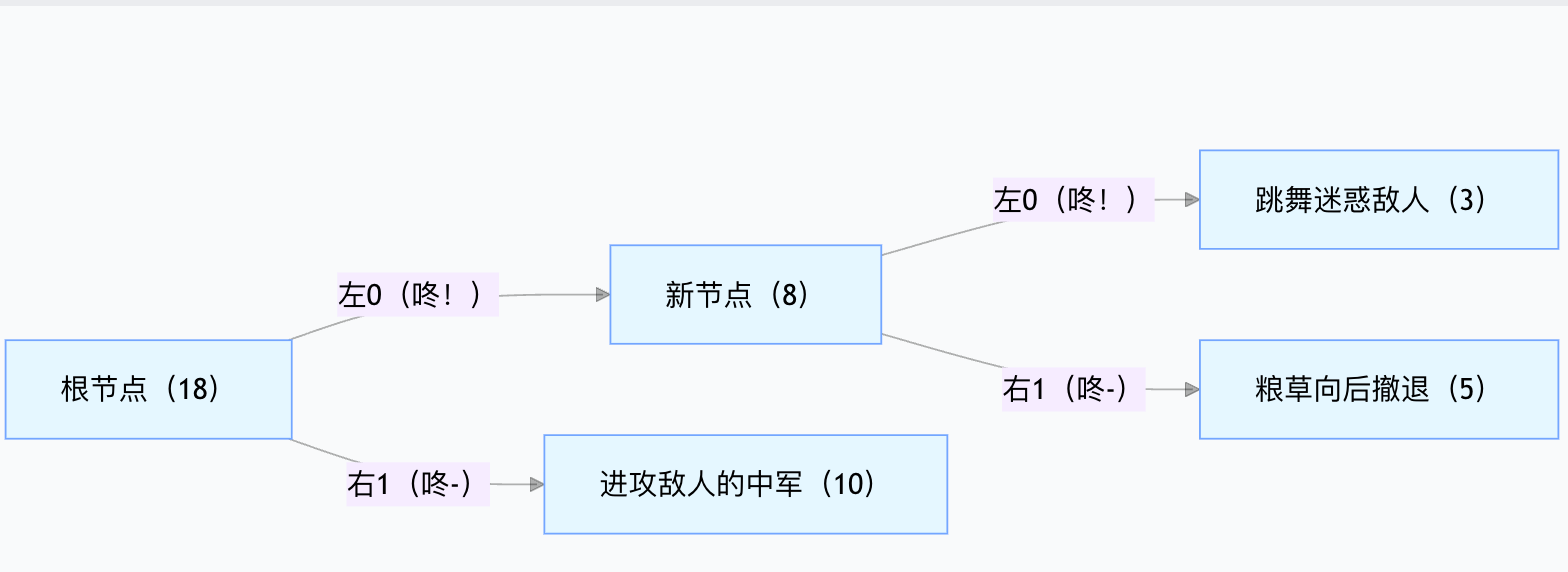
此时只剩 1 个根节点,霍夫曼树构建完成!
最终:从树到 “鼓响信号”
鼓响信号 = 从根节点到叶子节点的路径(0 = 短鼓 “咚!”,1 = 长鼓 “咚 -”,路径长度 = 鼓响次数):
| 传令指令 | 路径(根→叶子) | 鼓响信号 | 信号长度(鼓响次数) | 符合频率需求? |
|---|---|---|---|---|
| 进攻敌人的中军 | 右 1 | 咚 -! | 1 次 | 是(高频最短) |
| 粮草向后撤退 | 左 0→右 1 | 咚!咚 -! | 2 次 | 是(中频中等) |
| 跳舞迷惑敌人 | 左 0→左 0 | 咚!咚!咚! | 3 次 | 是(低频最长) |
构建规则总结
- 排序优先:每次合并前,先将所有节点按频率从小到大排序;
- 最小合并:只合并当前频率最小的两个节点,保证高频节点离根最近(路径最短);
- 路径编码:左分支 “0”、右分支 “1”,叶子节点的路径就是最终编码(鼓响信号)。
这样构建的霍夫曼树,完美实现 “高频指令短信号、低频指令长信号”,和军营 “少鼓响传急令、多鼓响传罕令” 的需求完全匹配!
三、霍夫曼编码的变种、注意点与调优
霍夫曼编码家族人丁兴旺,各有神通。
| 变种类型 | 核心思想 | 注意点 / 调优点 | 适用场景 |
|---|---|---|---|
| 静态霍夫曼编码 | 对整个数据集进行一次扫描,统计所有字符频率,然后生成一棵固定的霍夫曼树。 | 注意点:需要两次扫描数据(第一次统计频率,第二次编码),且需要将霍夫曼树本身作为额外信息存储或传输,对于小文件可能得不偿失。 | 适用于对完整文件进行压缩,如 gzip、zip 中的 DEFLATE 算法部分。 |
| 自适应(动态)霍夫曼编码 | 边读数据边更新霍夫曼树,无需预先统计频率。初始时所有字符频率相同,随着数据读入,动态调整树的结构。 | 调优点:实现复杂度更高,编码效率在初期可能不如静态版本。但无需存储树结构,适合流式数据。 | 实时通信、流媒体传输等无法预知全部数据或需要单次扫描的场景。 |
| 规范霍夫曼编码 | 一种静态霍夫曼的优化版本。它生成的编码具有“规范”形式:相同长度的编码,其数值是连续的。 | 调优点:解码器无需存储完整的树结构,只需存储每个编码长度的数量即可快速重建码本,解码速度更快,存储开销更小。 | 对解码性能和码本大小有严格要求的场景,如 JPEG 图像压缩标准。 |
四、在大数据及其他组件中的应用
霍夫曼编码作为熵编码的经典代表,早已渗透到我们数字生活的方方面面。
| 组件 / 领域 | 具体应用 | 编码角色 |
|---|---|---|
| 大数据存储 | Hadoop / Spark | 在使用 Gzip、Bzip2、DEFLATE 等压缩格式时,这些格式的核心算法都包含或借鉴了霍夫曼编码,用于压缩存储在 HDFS 上的数据,减少磁盘占用和网络传输开销。 |
| 数据序列化 | Apache Avro | Avro 的块压缩模式中,可以选择使用霍夫曼编码对序列化后的数据块进行压缩,提高存储和传输效率。 |
| 文件压缩 | Gzip, PNG, ZIP | Gzip 和 ZIP 使用的 DEFLATE 算法,是 LZ77 算法和霍夫曼编码的组合。LZ77 先做字符串替换,再用霍夫曼编码对替换结果和剩余字符进行终极压缩。PNG 也使用 DEFLATE 算法压缩图像数据。 |
| 多媒体编解码 | JPEG, MP3, H.264/AVC | 在 JPEG 图像压缩中,对 DCT 变换后的量化系数进行霍夫曼编码。在 MP3 和 H.264 等音视频编码标准中,也使用类似的熵编码技术(如 CAVLC/CABAC,其思想与霍夫曼一脉相承)来压缩变换系数和运动矢量等数据。 |
| 网络通信 | HTTP/2 (HPACK) | HTTP/2 的头部压缩算法 HPACK,虽然主要使用动态表,但其对整数字段的编码也采用了类似前缀码的思想,与霍夫曼编码异曲同工,旨在减少头部大小。 |
希望这场图文并茂的探险,能让你对霍夫曼编码有一个既生动又深刻的理解!
(欢迎订阅本专栏)
